Теоретическое введение: В.В.Белик, кафедра
физической химии РХТУ им. Д.И. Менделеева.
РАСЧЕТ ПАРЦИАЛЬНЫХ МОЛЯРНЫХ ВЕЛИЧИН
Для определения экстенсивного свойства однокомпонентной системы необходимо знать молярное, то есть рассчитанное на один моль компонента значение этого свойства. Зная молярное свойство и количество системы, можно получить общее значение этого свойства для всего количества системы.
Для характеристики отдельных компонентов в многокомпонентных растворах используют парциальные величины, определяющие некоторое свойство каждого компонента. Для определения парциальной молярной величины воспользуемся уравнением, определяющим функциональную зависимость некоторого экстенсивного параметра L состояния системы:
![]() (1)
(1)
где Т, Р – температура и давление и ![]() - число молей i – го компонента.
- число молей i – го компонента.
Например, для объема V:
![]()
Таким образом, многокомпонентная система может быть полностью характеризована числом молей всех ее компонентов, температурой и давлением.
Отметим, что экстенсивное свойство является функцией
состояния, то есть ее бесконечно малое приращение есть полный дифференциал.
Тогда из уравнения (1) следует:![]()
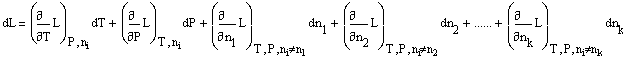
или:
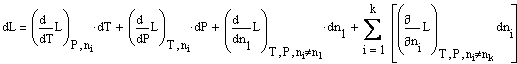
Введем обозначения:
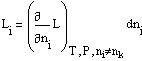
и
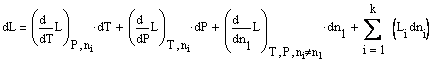
При постоянном давлении и температуре последнее уравнение принимает вид:
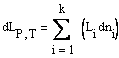
Величину
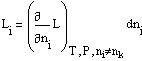
являющейся производной от общего свойства L по числу молей компонента i при постоянных значениях температуры, давления и числа молей всех остальных компонентов, называют парциальной мольной величиной компонента i.
По отношению к конечному значению некоторого свойства L парциальная мольная величина есть приращение свойства системы при добавлении в бесконечно большое ее количество одного моля компонента i.
Парциальные молярные величины ![]() - интенсивные
свойства, они зависят от состава, но не от количества системы (фазы, раствора).
- интенсивные
свойства, они зависят от состава, но не от количества системы (фазы, раствора).
Экстенсивные величины являются аддитивными функциями по отношению к парциальным молярным величинам:
![]()
Например, объем раствора
![]()
Каждое слагаемое в этом соотношении является вкладом i– го компонента в объем раствора.
Парциальный молярный объем, как и вообще парциальные молярные величины, учитывает все взаимодействия между компонентами реального раствора (фазы), поэтому может быть больше или меньше молярного объема чистого компонента, а в идеальном растворе равен ему.
В общем случае количество компонентов в системе могут изменяться произвольно, соответственно будут изменяться и состав системы, и значения парциальных молярных величин всех компонентов. Полный дифференциал от экстенсивного свойства системы, учитывающий все эти изменения, в соответствии с уравнением
![]()
равен:
![]()
Вычитая из 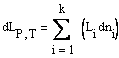
предыдущее соотношение, получим:
![]()
Разделив последнее соотношение на ![]() , получим уравнение
, получим уравнение
![]()
(где ![]() – молярная доля i-го
компонента), которое называют основным уравнением для парциальных молярных
величин.
– молярная доля i-го
компонента), которое называют основным уравнением для парциальных молярных
величин.
Для бинарного раствора, учитывая, что число
независимых концентраций (молярных долей) на единицу меньше числа компонентов,
и приняв за независимую переменную молярную долю второго компонента ![]() уравнению
уравнению
![]()
можно придать вид:
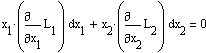
или
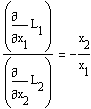
Анализируя последнее соотношение, можно сделать следующие выводы:
- парциальные молярные величины в бинарном растворе
изменяются антибатно, т.е. если для одного компонента парциальная молярная
величина растет с увеличением доли второго компонента ![]() , то для второго компонента она
уменьшается в этом направлении;
, то для второго компонента она
уменьшается в этом направлении;
- если на одной из зависимостей ![]() имеется максимум, то аналогичная
зависимость для другого компонента при этом же составе системы будет иметь
минимум;
имеется максимум, то аналогичная
зависимость для другого компонента при этом же составе системы будет иметь
минимум;
- при равных молярных долях компонентов производные свойства равны по абсолютной величине, но имеют разные знаки.
Аналитический расчет парциальных молярных величин сводится к аппроксимации полиномом n –ой степени экспериментальной зависимости между данным экстенсивным свойством и составом раствора (например, его моляльности) и его дифференцировании.
Расчет парциальных молярных величин реализован в (1) и (2):
- Расчет парциальных мольных объемов компонентов в бинарных растворах >>>
- Расчет парциальных мольных энтальпий растворения компонентов в бинарных растворах >>>