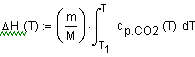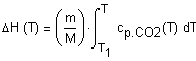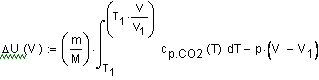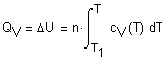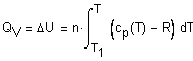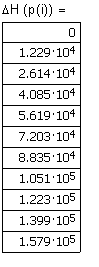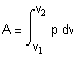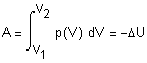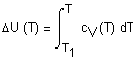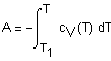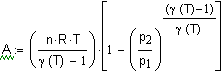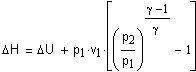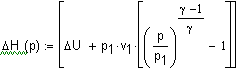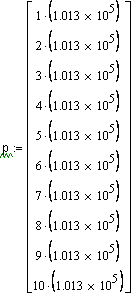|
РАСЧЕТНЫЕ ЗАДАЧИ |
ПРЕДИСЛОВИЕ
При изучении любого
физико-химического процесса исследователя (или технолога) обычно интересуют
несколько вопросов:
1. Возможно ли осуществление
рассматриваемого процесса в заданных условиях, то есть при определенных
значениях температуры, давления, концентраций компонентов реакции?
2. Если
возможно, то с какими энергетическими изменениями
связано протекание процесса в заданных условиях? 3. Если в заданных условиях протекание процесса
возможно, то насколько полно он будет протекать в этих условиях? Как изменится
концентрация исходных веществ и продуктов реакции? Каковы будут
значения концентраций реагентов при достижении реакционно-способной системы
равновесного состояния? 4. Если
протекание процесса в заданных условиях невозможно, то как надо изменить условия, чтобы процесс был осуществим с
необходимой полнотой или необходимой степенью превращения? 5. Как
быстро будет достигнуто состояние равновесия? Подход к ответам на первые четыре
вопроса дает термодинамика – учение о связи и взаимопревращениях различных
видов энергии, теплоты и работы. Термодинамика не может дать ответа
на пятый вопрос: это область химической кинетики, изучающей скорости
химических превращений. Иллюстрацией подходов к возможным ответам на первые
четыре вопроса посвящен настоящий курс. Курс состоит из четырех глав,
каждая из которых тематически объединяет обзор основных законов и
закономерностей, а так же определенный класс задач. Рассматриваются конкретные задачи, иллюстрирующие
возможности описанных методов. Курс построен по методу информационного
моделирования. Информационное
моделирование как метод познания предполагает создание информационной среды,
включающей в себя: - тематическое
объединение обзора основных задач, стоящих перед исследователем в
предполагаемой профессиональной деятельности, их структурирование, - обзор
основных законов и закономерностей, с помощью которых эти задачи могут быть
решены, -модель
процедуры решения типовых репродуктивных учебных задач типа “образец“, -возможность
планирования обучения на основе решения задачи как некоторой редакции “образца“ по определенному
сценарию, -получение новых знаний за счет обобщений,
полученных после решения комплекса определенных задач. Такой подход к созданию информационно-учебной среды должен способствовать развитию познавательной активности обучающегося, предоствляя ему возможность получения не только учебных, но и научных знаний, ставить перед студентом исследовательские задачи. |
|
ГЛАВА
1 ТЕПЛОЕМКОСТЬ.
ЭНТАЛЬПИЯ. ТЕМПЕРАТУРНАЯ ЗАВИСИМОСТЬ
ЭНТАЛЬПИИ ВЕЩЕСТВ. 1.1 Цели изучения. Изучив этот
раздел, вы сможете: - различать теплоемкости в изохорном и изобарном
процессах; - рассчитывать теплоемкости веществ в зависимости
от температуры; - рассчитывать изменение энтальпии веществ при изменении температуры; - рассчитывать изменение энтальпии веществ при фазовых и модификационных переходах; - рассчитывать аккумулирующую способность тепловой энергии
некоторыми веществами; - рассчитывать теоретическую температуру горения. 1.2. Основные
понятия и закономерности. Теплоемкость (Heat capacity) определяют как
производную от количества теплоты по температуре в каком-либо
термодинамическом процессе: Теплоемкость зависит от условий, при которых
протекает процесс (поскольку от этих условий зависит количество теплоты). В изохорном
процессе (Isochoric process) и в изобарном процессе (Isobaric
process) где U и Н
внутренняя энергия (Internal energy)
и энтальпия (Enthalpy) вещества соответственно. Теплоемкость является экстенсивной величиной (так же как внутренняя
энергия и энтальпия), т.е. величиной, пропорциональной количеству вещества.
Поэтому в практических приложениях используют как удельную теплоемкость,
отнесенную к единице массы вещества, так и молярную теплоемкость, отнесенную к молю вещества,которые связаны
соотношением: где М - молекулярная масса вещества. Изменение энтальпии вещества при увеличении
температуры от Во всей
температурной области существования данной фазы энтальпия вещества является
монотонно возрастающей функцией. Если в рассматриваемом интервале температур происходят изменения
фазовых состояний системы, то в выражении (1.4) необходимо учесть энтальпии
соответствующих
фазовых переходов. Температурная зависимость теплоемкости обычно задается в виде степенного ряда: для неорганических веществ и для органических веществ коэффициенты которого a, b, Интегрирование (1.4) с учетом (1.5) и (1.6)
приводит к выражению: В некоторых случаях удобно использовать среднюю теплоемкость Cредние теплоемкости для многих веществ
приведены в справочниках[1-3]. В некоторых случаях удобно использовать данные о приращении энтальпии
|
|
Следует учесть, что
величина
Если значения
теплоемкости для некоторых твердых и жидких веществ отсутствуют в справочных
данных, то в [1] рекомендуют рассчитывать их (при 298К)
по атомным теплоемкостям. Важной для подбора
материала и для выяснения возможности превращения теплоты в работу является теоретическая
температура горения - температура, которая достигается при полном
и адиабатном сгорании газообразного топлива. Расчет теоретической
температуры горения
где |
|
При усвоении наук примеры полезнее правил. ИСААК НЬЮТОН. 1.3. Основные задачи. Основной прикладной
задачей является расчет значений Под аккумулированием
на основе теплоты фазового перехода понимается аккумулирование теплоты
плавления, происходящее обычно с небольшими изменениями объема. Иногда
фазовый переход твердое тело жидкость совмещается с фазовым переходом твердое
тело - твердое тело (например, - переходом) при
температуре несколько ниже точки плавления. Часто в дополнение к
теплоте фазового перехода предлагается использовать теплоту нагрева жидкости
и/или твердого тела. Это увеличивает емкость теплового аккумулятора, однако
лишает воз- можности использовать преимущества отбора тепла при
постоянной температуре. Включение
теплоаккумулирующей системы в теплосиловую схему АЭС или АТЭЦ
позволяет решить (или по крайней мере уменьшить)
проблемы покрытия пиков тепловой и электрической нагрузки. Создание тепловых
солнечных электростанций (СЭС) так же вызывает
необходимость использования теплоаккумулирующих систем с диапазоном
температур 200 -450С для солнечных ферм и 700- 900С для СЭС. Количество тепловой
энергии s, которое может быть
аккумулировано в единице объема вещества, определяется согласно: где V(м3/кмоль) - мольный объем, cр = cр(Т)-
теплоемкость (Дж/кг К), - плотность (кг/м3), |
|
Если
использовать средние ( в заданном температурном
интервале) значения
теплоемкости c и плотности ,
то объемную плотность аккумулирован- ной энергии s можно
рассчитать по соотношению (1.11):
где К общим
требованиям для теплоаккумулирующих материалов ( в добавле- нии к очевидным - высокой теплоемкости и высокой теплоты плавления ) относят термическую и химическую стабильность, некоррозионность по отношению к конструкционным материалам и высокую теплопроводность. |
|
Задача 1.3.1,
в которой вычислена средняя мольная теплоемкость аммиака Задача 1.3.2,
в которой определены средние значения теплоемкости NaOH
интервале температур 298 - 1000К. Задача 1.3.3,
в которой рассчитаны,используя
истинные значения теплоемкостей, изменениe
энтальпии Задача 1.3.4, в которой рассчитаны изменение энтальпии Задача 1.3.5,
в которой рассчитана удельная h, кДж/ кг, и объемная s,
мДж/м3, плотности аккумулированной тепловой энергии
в интервале температур Задача 1.3.6,
в которой рассчитана удельная h, кДж/ кг, и объемная s,
мДж/м3, плотности аккумулированной тепловой энергии
в интервале температур Задача 1.3.7,
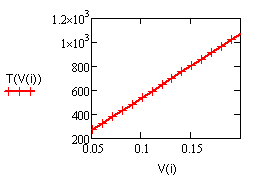
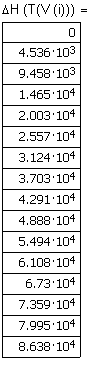
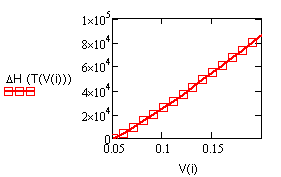
в которой исследуется влияние температуры Т на
удельную h и объемную s плотности аккумулированной
тепловой энергии при нагревании воды от температуры Задача 1.3.8,
в которой выведено уравнение зависимости изменения энтальпии Задача 1.3.9,
в которой определена теоретическая температура горения Задача 1.3.10, в которой определена теоретическая температура горения метана со 150%
избытком воздуха, если температура метана и воздуха равна 273К. Задача 1.3.11, в которой определены максимальная температура и максимальное
давление, которые реализуются при взрыве в закрытом сосуде при 298К и давлении 1 атмосфера смеси моля водорода и
теоретического количества воздуха. Задача 1.3.12,
в которой по температурной зависимости теплоемкости газообразной двухатомной
серы найдено уравнение зависимости Задача 1.3. 13, в которой по данным о температурной зависимости мольной
теплоемкости (Дж/мольК) водяного пара определено
количество теплоты, выделевшееся при охлаждении 90г пара от 580 до 373К при
постоянном давлении 1 атм. Задача 1.3.14, в которой в зависимости от начальной температуры Т
водяного пара определено количество теплоты, выделевшееся
при охлаждении 100г пара от температуры Т до 373К при постоянном давлении 1 атм. Задача 1.3.15, в которой в зависимости от массы водяного пара определено количество
теплоты, выделевшееся при его охлаждении от
температуры 673К до 373К
при постоянном давлении 1 атм. Задача 1.3.16, в которой по экспериментальным данным о зависимости мольной
теплоемкости
|
|
Задача 1.3.17,
в которой поэкспериментальнонайденнымзначенияммольнойтеплоемкости(Дж/мольK)
оксидауглеродаприсоответствующихтемпературахопределено
уравнение Задача 1.3.18, вкоторой определена теплотаQ, работаA, изменениевнутреннейэнергии m = 100г., находящегосяпри273Кидавлении1
атм. ( Задача 1.3.19,
вкоторойопределенытеплотаQ,
работаA, изменениевнутреннейэнергии Задача 1.3.20, вкоторойопределенаработаиспарения3 молейметанолапринормальнойтемпературекипения. |
|
Задача
1.3.1. Вычислите
среднюю мольную теплоемкость аммиака Решение. Для
определения средней мольной теплоемкости воспользуемся соотношением (1.8) Зависимость
теплоемкости аммиака Тогда: |
|
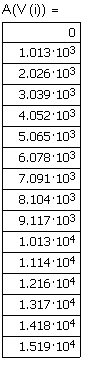
Ввод температур, в
интервале которых определена средняя мольная теплоемкость аммиака |
|
|
|
|
|
|
|
Ввод соотношения, определяющего среднюю мольную теплоемкость. |
|
Вывод резудьтата - средняя мольная теплоемкость (Дж/мольК) аммиака в интервале температур 300 - 400К. |
|
|
|
Задача 1.3.2. Определите
средние значения теплоемкости c NaOH
интервале температур 298 - 1000К. Решение. Для
определения средней мольной теплоемкости воспользуемся соотношением (1.8) Теплоемкость твердого - NaOH в интервале
температур 298 - 566К описывается соотношением
|
|
Притемпературе566К происходитмодификационное -> превращение - NaOH
-----> - NaOH. Ксожалению, данныеокоэффициентахуравнения Притемпературе595Кпроисходитплавление- NaOH
степлотойплавления H = 6.36 кДж/моль. Ддяжидкого Рассчитаемвначалесредниезначениятеплоемкостидлятвердого |
|
|
|
Ввод ранжированной переменной - тем- пературы.( 305 - 595К) |
|
|
|
Ввод функции, определяющей зависимость теплоемкости твердого - NaOH от температуры |
|
|
|
Ввод функции, определяющей зависимость средней теплоемкости твердого - NaOH от температуры |
|
|
|
|
|
|
|
|
|
|
|
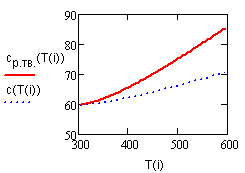
Вывод результата счета - зависимость
теплоемкости |
|
Результат счета иллюстрирует рис. 2.1. |
|
|
|
Рис. 2.1.
Зависимость теплоемкости |
|
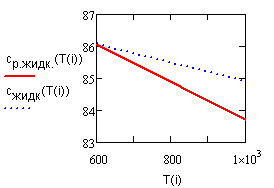
Теперь рассчитаем температурную зависимость
теплоемкости для жидкого состояния NaOH Ддя жидкого
|
|
|
|
Ввод ранжированной переменной - температуры.( 595 - 1000К) |
|
|
|
Ввод функции, определяющей зависимость теплоемкости жидкого NaOH от температуры |
|
|
|
Ввод функции, определяющей зависимость средней теплоемкости жидкого NaOH от температуры |
|
|
|
|
|
|
|
|
|
Вывод результата
счета - зависимость теплоемкости |
|
Результат счета иллюстрирует рис. 2.2 |
|
|
|
Рис.2.2.
Зависимость теплоемкости |
|
Задача 1.3.3. Рассчитайте изменение энтальпии
Решение. Рассчитаем Расчет будем вести по формуле Тогда в области температур от 298К до температуры плавления где и в области температур, больших температуры плавления где |
|
|
|
Ввод ранжированной переменной - температуры. Температура изменяется от 300 до 1000К. |
|
|
|
|
|
|
|
|
|
Вывод результата счета - зависимость изменения энтальпии NaOH от температуры в интервале температур 300 - 1000К. |
|
|
|
Рис. 3.1. Зависимость изменения энтальпии NaOH от температуры в интервале температур 300 - 1000К. |
|
Задача 1.3.4 Рассчитайте изменение энтальпии Сравните полученные результаты. Решение.
В области температур до температуры плавления изменение энтальпии
где eee, iianoaaea caaeneiinou oaieiaieinoe io oaiia?aoo?u: В области температур выше температуры плавления изменение энтальпии будем рассчитывать по соотношению в котором
теплоемкость жидкого вещества |
|
|
|
Ввод ранжированной переменной - температуры. Температура изменяется от 345 до 995К. |
|
|
|
Ввод соотношения,
определяющего температурную зависимость истинной мольной теплоемкости от
температуры NaOH в области температур до
температуры плавления |
|
|
|
Ввод соотношения,
определяющего температурную зависимость средней мольной теплоемкости от
температуры NaOH в области температур до
температуры плавления |
|
|
|
|
|
Ввод начальной температуры. |
|
Ввод соотношения, определяющего зависимость изменения энтальпии
|
|
|
|
Ввод соотношения,
определяющего температурную зависимость истинной мольной теплоемкости от
температуры жидкого NaOH в области температур от
температуры плавления |
|
|
|
Ввод температуры плавления NaOH, К. |
|
|
|
|
|
Ввод теплоты плавления, Дж/моль |
|
Ввод соотношения,
определяющего температурную зависимость средней мольной теплоемкости от
температуры жидкого NaOH в области температур от
температуры плавления |
|
|
|
Ввод соотношения, определяющего зависимость изменения энтальпии
|
|
|
|
Тогда изменение энтальпии NaOH |
|
|
|
Вывод результата счета - изменение энтальпии
NaOH |
|
|
|
|
|
|
|
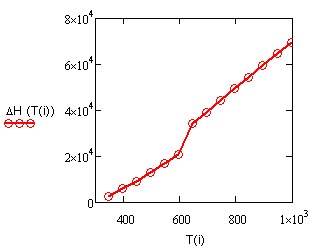
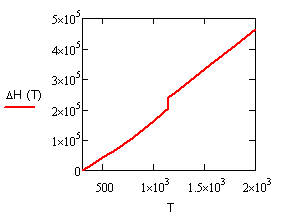
Рис. 4.1. Изменение
энтальпии |
|
Задача 1.3.5.
Известен экологически чистый способ аккумулирования тепловой энергии, основанный на использовании теплоты фазового перехода плавление-кристаллизация. Во время плавления температуры вещества остается постоянной до расплавления всей массы вещества. При охлаждении происходит обратный процесс кристаллизация с выделением аккумулированной теплоты. Обычно процесс проводят в области температур
Рассчитайте удельную h, кДж/ кг, и объемную s, мДж/м3, плотности
аккумулированной тепловой энергии в интервале температур Решение. Поскольку интервал температур достаточно
мал, то удельную плотность h аккумулированной тепловой энергии ( в интервале температур где Или, поскольку
Тогда: |
|
|
|
Ввод значений средней уделной
теплоемкости твердой |
|
|
|
Ввод удельной теплоты плавления, кДж/ кг |
|
|
|
|
|
Ввод интервале температур |
|
Ввод соотношения,
определяющего зависимость удельной плотности h аккумулированной тепловой
энергии ( в интервале температур |
|
|
|
Вывод результата
счете - удельная h, кДж/ кг, плотность аккумулированной тепловой энергии в
интервале температур |
|
|
|
Теперь рассчитаем объемную s, мДж/м3, плотность
аккумулированной тепловой энергии в том же интервале температур |
|
|
|
Ввод значений средней плотности твердой |
|
|
|
|
|
Ввод удельной теплоты плавления, кДж/кг |
|
Ввод соотношения, определяющего зависимость
объемной плотности s аккумулированной тепловой
энергии ( в интервале температур |
|
|
|
Вывод результата -
объемной плотности аккумулированной тепловой энергии s,
мДж/м3, в интервале температур |
|
|
|
Задача 1.3.6. Известен экологически чистый способ аккумулирования тепловой энергии, основанный на использовании теплоты фазового перехода плавление-кристаллизация. Во время плавления температуры вещества остается постоянной до расплавления всей массы вещества. При охлаждении происходит обратный процесс кристаллизация с выделением аккумулированной теплоты. Обычно процесс проводят в области температур
Рассчитайте удельную h, кДж/ кг, и объемную s, мДж/м3, плотности
аккумулированной тепловой энергии в интервале температур Решение. Задача аналогична
предыдущей, однако, температура плавления додекагидрата
сульфата алюминия Поскольку интервал температур достаточно
мал, то удельную плотность h аккуму- лированной тепловой энергии (
в интервале температур где Или, поскольку
|
|
|
|
Ввод значений средней уделной
теплоемкости твердой |
|
|
|
|
|
Ввод удельной теплоты плавления, кДж/ кг |
|
|
|
Ввод интервале температур |
|
Ввод соотношения,
определяющего зависимость удельной плотности h аккумулированной тепловой
энергии ( в интервале температур |
|
|
|
Вывод результата счета - удельная h, кДж/ кг, плотность
аккумулированной тепловой энергии в интервале температур |
|
|
|
Теперь определим
объемную s, мДж/м3,
плотность аккумулированной тепловой энергии в том же интервале температур |
|
|
|
Ввод значений средней уделной
теплоемкости твердой |
|
|
|
|
|
Ввод значений средней плотности твердой |
|
|
|
Ввод удельной теплоты плавления, кДж/ кг |
|
|
|
Ввод интервале температур |
|
|
|
Ввод соотношения,
определяющего зависимость объемной плотности s
аккумулированной тепловой энергии ( в интервале
температур |
|
|
|
Вывод результата
счета - объёмная s, мДж/м3,
плотность аккумулированной тепловой энергии в интервале температур |
|
|
|
Полученные результаты позволяют сделать следующие выводы: - рассмотренный способ аккумулирования тепловой энергии дает возможность проводить отбор тепловой энергии при практически постоянной температуре, поскольку при кристаллизации температура остается постоянной; - рассмотренный способ аккумулирования тепловой энергии дает возможность вариировать эту температуру за счет подбора соединений с температурой плавления в необходимом температурном интервале. |
|
Задача 1.3.7. Исследуйте влияние температуры Т на удельную h и объемную s
плотности аккумулированной тепловой энергии при нагревании воды от
температуры Определите удельную и объемную плотности
аккумулированной тепловой энергии при нагревании воды от температуры Обсудите недостатки такого способа аккумулирования тепловой энергии. Решение. При нагревании веществ от
температуры |
|
Тогдавобластитемпературот где дляжидкойводывинтервалетемператур273 - 373
Тогда
иудельнаяh иобъемнаяs
плотностиаккумулированнойтепловойэнергиипринагреванииводыоттемпературы где n - числомолейводыводномкилограме и где ПроследимвлияниетемпературыТнаудельнуюh
иобъемнуюs
плотностиаккумулированнойтепловойэнергиипринагреванииводыоттемпературы |
|
Ввод ранжированной переменной - темпера - туры. Температура изменяется от 273 до 373К через 10 градусов. |
|
|
|
|
|
Ввод числа молей воды в одном килограмме воды (считая плотность воды 1кг/дм3) |
|
|
|
Ввод соотношения, определяющего удельную плотность аккумулированной тепловой энергии в зависимости от начальной температуры до температуры кипения. |
|
|
|
|
|
|
|
Вывод результата счета - удельная плотность аккумулированной тепловой энергии в зависимости от начальной температуры до температуры кипения. |
|
|
|
Рис. 7.1. Удельная плотность аккумулированной тепловой энергии жидкой воды в зависимости от начальной температуры до температуры кипения. |
|
Теперь определим объемную s, мДж/м3, плотность аккумулированной тепловой энергии в интервале температур T - 373К. Считая плотность жидкой воды 1000 кг/м3, определим число молей n воды в одном кубическом метре: |
|
Ввод массы, кг, одного кубического метра воды. |
|
|
|
Ввод молярной массы, кг/моль воды. |
|
|
|
Ввод соотношения, определяющего число молей n воды в одном кубическом метре. |
|
|
|
|
|
Вывод результата - число молей воды в одном кубическом метре. |
|
|
|
Вывод результата счета - объёмная плотность аккумулированной тепловой энергии при нагревании от начальной температуры 273К до температуры кипения. |
|
|
|
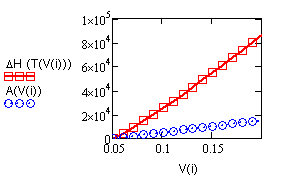
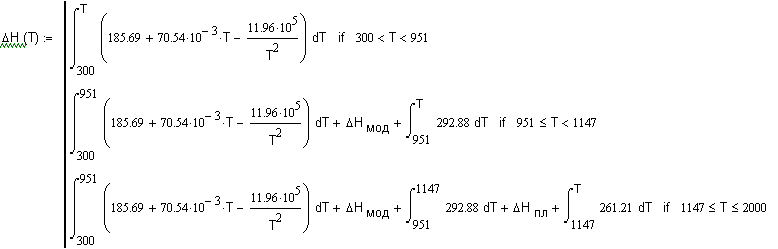
Задача 1.3.8. Выведите уравнение зависимости изменения энтальпии
Решение. Прежде всего приведем необходимые справочные данные. В интервале
температур 298 < T< 951K зависимость мольной
теплоемкости - При 951К происходит модификационное -----> превращение - с тепловым эффектом H = 420 Дж/моль В интервале температур 951- 1147К зависимость мольной теплоемкости - При 1147Т - - с тепловым эффектом
И в области
температур 1147 - 2000К зависимость мольной
теплоемкости жидкого
|
|
Тогда |
|
Ввод значений теплового эффекта модификационного - превращения |
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 8.1.
Зависимость изменения энтальпии |
|
Задача 1.3.9. Определите теоретическую температуру горения
Решение.
Примем, что воздух состоит из 79% азота и 21% кислорода, и диссоциацией оксида углерода пренебрежём. Тогда теоретическую температуру горения |
|
где где Посколькупроцесс протекаетполностьюиадиабатно,
товыделяющаясяприэтомтеплотареакции Необходимыедлярасчетаданные- температурныезависимоститеплоемкостей(Дж/мольК) диоксидауглерода, инертноговещества(азота) итеплотыобразования(298К) оксидауглеродаидиоксидауглерода (Дж/моль) возьмемвсправочнике: |
|
|
|
Ввод температурных зависимостей теплоемкости (Дж/мольК) диоксида углерода и азота. |
|
|
|
|
|
Ввод теплоты образования (298К) оксида углерода и диоксида углерода (Дж/моль) |
|
|
|
Ввод соотношения, определяющего тепловой эффект исследуемой реакции. |
|
|
|
В силу полноты реакции и адиабатности процесса теплота реакции сгорания оксида углерода расходуется на нагревание одного моля диоксида углерода и |
|
Ввод начальной температуры. |
|
|
|
Ввод числа молей азота |
|
|
|
|
|
Ввод ключевого слова. |
|
|
|
Ввод соотношения, определяющего уравнение относительно Т - теоретической температуры горения. |
|
|
|
Вывод результата решения уравнения - теоретическая температура горения оксида углерода СО с теоретически необходимым количеством воздуха при давлении 1 атм. и начальной температуре 298К. |
|
|
|
Задача 1.3.10. Определите теоретическую температуру горения метана с 150% избытком воздуха, если температура метана и воздуха равна 273К. Решение. Уравнение процесса сгорания метана |
|
тогда теоретическаятемпературагоренияметана со150% избытком воздухапридавлении1 атм. и начальнойтемпературе298Кможетбытьнайденаизсоотношения
Необходимыедлярасчетаданные- температурныезависимоститеплоемкостей(Дж/мольК) диоксидауглерода, инертноговещества(азота), метана, кислорода итеплотыобразования(298К) диоксидауглерода, водыиметана- длярасчетатемпературнойзависимоститепловогоэффектареакции (Дж/моль) - возьмемвсправочнике: |
|
|
|
|
|
Ввод температурных зависимостей
теплоемкостей |
|
|
|
|
|
|
|
|
|
|
|
Ввод температурных
зависимостей изменения теплоемкостей в реакции образования метана |
|
|
|
|
|
|
|
Ввод теплот образования воды, диоксида углерода и метана при298К. |
|
|
|
|
|
Ввод соотношений, определяющих температурные зависимости тепловых эффектов реакций образования воды, метана и диоксида углерода. |
|
|
|
|
|
Ввод соотношения, определяющего температурную зависимость теплового эффекта исследуемой реакции горения метана. |
|
|
|
Ввод начальной температуры. |
|
|
|
Ввод ключевого слова. |
|
|
|
Ввод соотношения, определяющего уравнение
относительно Т - теоретической температуры горения.
Поскольку соотношение азот:кислород
в воздухе как |
|
|
|
Вывод результата решения уравнения - теоретическая температура горения метана с 150% избытком воздуха, если температура метана и воздуха равна 298К. |
|
|
|
Задача 1.3.11. Определите максимальную температуру и максимальное давление, которые реализуются при взрыве в закрытом сосуде при 298К и давлении 1 атмосфера смеси моля водорода и теоретического количества воздуха. Решение. Исследуемая реакция протекает при постоянном объеме, поэтому ее тепловой эффект равен изменению внутренней энергии Тогда максимальная температура, которая реализуются при взрыве в закрытом сосуде при 298К и давлении 1 атмосфера смеси моля водорода и теоретического количества воздуха может быть рассчитана по соотношению: где и Необходимые для расчета данные - температурные зависимости теплоемкостей (Дж/мольК) водорода, кислорода, воды, инертного вещества (азота) и теплоту образования воды - для расчета температурной зависимости теплового эффекта реакции (Дж/моль) - возьмем в справочнике: |
|
Ввод значения |
|
|
|
|
|
Ввод соотношений, определяющих температурные зависимости теплоемкостей (Дж/мольК) газообразной воды и азота. |
|
|
|
Ввод соотношения, определяющего температурную зависимость изменения теплоемкости (Дж/мольК) в реакции образования газообразной воды. |
|
|
|
Ввод значения теплоты образования газообразной воды при 298К. |
|
|
|
Ввод соотношения, определяющего температурную зависимость теплоты образования (Дж/моль) газообразной воды. |
|
|
|
|
|
Ввод соотношения, определяющего температурную зависимость измене- ния внутренней энергии (теплового эффекта реакции при постоянном объеме) в реакции образования (Дж/моль) газообразной воды. |
|
|
|
Теплота реакции
Так как взрыв является адиабатным процессом,
то теплота реакции где и Задача по определению максимальной температуры, которая реализуются при взрыве в закрытом сосуде при 298К и давлении 1 атмосфера смеси моля водорода и теоретического количества воздуха сводится к решению уравнения
относительно температуры Т. Решим это уравнение. |
|
|
|
Ввод соотношений, определяющих температурные зависимости теплоемкостей при постоянном обэеме Дж/мольК) газообразной воды и азота. |
|
|
|
Ввод начальной температуры. |
|
|
|
Ввод ключевого слова. |
|
|
|
Ввод соотношения, определяющего решаемое уравнение. |
|
|
|
Вывод результата решения уравнения - температура (К), которая реализуется при взрыве в закрытом сосуде при 298К и давлении 1 атм. смеси моля водорода и теоретического количества воздуха. |
|
|
|
Отметим, что полученный результат является достаточно приближенным, поскольку при решении не учитывалась диссоциация паров воды при таких высоких температурах. ( Степень диссоциации водяного пара при 3000К составляет около 16%). Теперь рассчитаем давление, которое реализуется при взрыве в закрытом сосуде при 298К и давлении 1 атм. смеси моля водорода и теоретического количества воздуха. Согласно уравнению Клапейрона - Менделеева Поскольку процесс протекает при постоянном объеме V, то для двух состояний системы - исходному (до взрыва) и конечному (лосле взрыва) - можно записать: |
|
Или
Подставимвполученноевыражениечисловыезначения: |
|
Ввод значения исходного давления, атм. |
|
|
|
Ввод значения исходного числа молей. |
|
|
|
Ввод значения конечного числа молей. |
|
|
|
|
|
Ввод значений исходной температуры, К. |
|
Ввод значений конечной температуры, К |
|
|
|
Ввод соотношения, определяющего конечное давление. |
|
|
|
Вывод результата - давление (атм.), которое реализуется при взрыве в закрытом сосуде при 298К и давлении 1 атм. смеси моля водорода и теоретичес- кого количества воздуха.
|
|
|
|
Задача 1.3.12. Температурная зависимость теплоемкости газообразной двухатомной серы выражается уравнением Найдите уравнение зависимости Решение. Уравнение
или для исследуемого случая Дальнейшее не представляет труда: |
|
Ввод подинтегральной функции. Выделение переменной Т и выполнение команды Simbolics/Variable/Integrate. |
|
|
|
Аналитическое выражение неопределенного интеграла. |
|
|
|
Следовательно, искомое уравнение температурной зависимости изменения энтальпии двухатомной газообразной серы Теперь можно рассчитать изменение энтальпии
газообразной |
|
|
|
Ввод ранжированной переменной - температуры Т, которая изменяется в интервале 300 - 3000К через 100К. |
|
|
|
Ввод соотношения, определяющего температурную зависимость изменения энтальпии двухатомной газообразной серы |
|
|
|
|
|
|
|
Вывод результата счета - температура, К и соответствующие ей значения изменения энтальпии двухатомной газообразной серы |
|
|
|
Рис. 1.12. . Температурная зависимость изменения энтальпии двухатомной газообразной серы. |
|
Задача 1.3. 13 Температурная зависимость мольной теплоемкости (Дж/мольК) водяного пара можно выразить соотношением Определите количество теплоты, выделевшееся при охлаждении 90г пара от 580 до 373К при постоянном давлении 1 атм. Решение. Теплота, выделевшаяся при охлаждении 90г пара от 580 до 373К при постоянном давлении 1 атм. может быть рассчитана по соотношению Подставим в это выражение необходимые данные: |
|
Ввод молярной массы (г/моль) водяных паров. |
|
|
|
Ввод числа молей водяных паров, содержащихся в 90г. |
|
|
|
Ввод соотношения, определяющего температурную зависимость теплоемкости водяных паров. |
|
|
|
Ввод соотношения, определяющего теплоту, выделевшеюся при охлаждении 90г. водяных паров от температуры 580 до 373К. |
|
|
|
|
|
Вывод результата - теплота (Дж), выделевшеюся при охлаждении 90г. водяных паров от температуры 580 до 373К. |
|
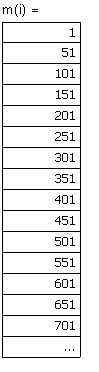
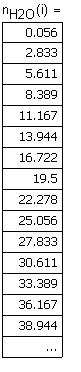
Задача 1.3.14. Температурная зависимость мольной теплоемкости (Дж/мольК) водяного пара можно выразить соотношением Определите зависимость количества теплоты, выделевшейся при охлаждении 100г пара от температуры Т до 373К при постоянном давлении 1 атм. Решение. Теплота, выделевшаяся при охлаждении 100г пара от 580 до 373К при постоянном давлении 1 атм. может быть рассчитана по соотношению Зависимость Подставим в это выражение необходимые данные: |
|
Ввод молярной массы (г/моль) водяных паров. |
|
|
|
Ввод числа молей водяных паров, содержащихся в 100г. |
|
|
|
Ввод соотношения, определяющего температурную зависимость теплоемкости водяных паров. |
|
|
|
|
|
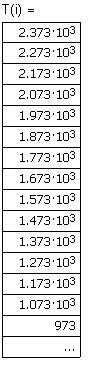
Ввод ранжированной переменной - температуры Т. Температура изменяется от 2373 до 373К. |
|
|
|
Ввод соотношения, определяющего теплоту, выделевшеюся при охлаждении 100г. водяных паров от температуры Т до 373К. |
|
|
|
|
|
|
|
Вывод результата - температура и соответствуюшая ей теплота (Дж), выделевшеюся при охлаждении 100г. водяных паров от температуры 2373 до 373К. |
|
|
|
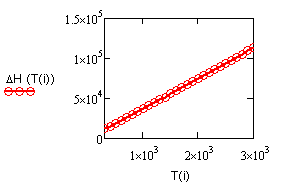
Рис. 14.1. Зависимость теплоты (Дж), выделевшеюся при охлаждении 100г. водяных паров от начальной температуры Т до 373К. |
|
Задача 1.3.15. Определите количество теплоты, выделевшееся при охлаждении водяного пара от температуры 673К до 373К при постоянном давлении 1 атм. в зависимости от массы водяного пара. Решение. Теплота, выделевшаяся
при охлаждении Подставим в это выражение необходимые данные: |
|
Ввод молярной массы (г/моль) водяных паров. |
|
|
|
|
|
Ввод ранжированной переменной - массы водяных паров. Масса изменяется от 1 до 1000г. |
|
|
|
Ввод числа молей
водяных паров, содержащихся в |
|
|
|
Ввод соотношения, определяющего температурную зависимость теплоемкости водяных паров. |
|
|
|
Ввод соотношения, определяющего теплоту (Дж), выделевшуюся при охлаждении m г. водяных паров от температуры 673 до 373К. |
|
|
|
|
|
|
|
|
|
Вывод результата -число молей водяных паров, содержащихся в m г. и теплота (Дж), выделевшаяся при охлаждении m г. водяных паров от температуры 673 до 373К. |
|
|
|
Рис. 15. 1. Теплота (Дж), выделевшаяся при охлаждении водяных паров от температуры 673 до 373К в зависимости от массы водяных паров. |
|
Задача 1.3.16.
Зависимость мольной теплоемкости |
|
Найдитенаоснованииэтихданныхуравнениетемпературнойзависимостиацетилена
Решение. Решениебудемискатьввидеуравненеия зависимости посколькудляорганическихсоединенийуравнениятакоговиданаиболееадекватноописываютвлияниетемпературынатеплоемкость.
ВMathcad реализованаполиноминальнаярегрессия, котораяпредставляетприближениеданных(
|
|
|
|
Ввод вектора действительных данных аргумента. |
|
Ввод вектора действительных данных значений. |
|
|
|
|
|
Ввод степени полинома регрессии. |
|
Вектор коэффициентов для построения полиноминальной регрессии данных. |
|
|
|
|
|
Вывод результата - значения коэффициентов полиноминальной регрессии. |
|
Следовательно, искомое уравнение температурной зависимости теплоемкости ацетилена: |
|
|
|
Сопоставим опытные |
|
|
|
|
|
|
|
Графическая иллюстрация полученных результатаов представлена на рис. 16.1. |
|
|
|
Рис. 16.1.
Сопоставление опытных значений теплоемкости ацетилена в зависимости от температуры. |
|
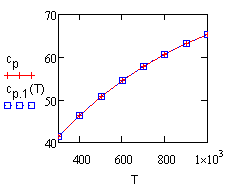
Задача 1.3.17. Экспериментально найденные значения мольной теплоемкости (Дж/мольK) оксида углерода при соответствующих температурах выражаются следующими данными: Определите по эти данным уравнение зависимости мольной теплоемкости оксида углерода от температуры. Решение.
Решение будем искать в виде уравненеия зависимости поскольку для неорганических соединений уравнения такого вида наиболее адекватно описывают влияние температуры на теплоемкость.
В Mathcad реализована регрессия общего вида, которая представляет возможность осуществить регрессию в виде линейной комбинации любых функций пользователя . где Используя регоессию этого типа, найдем уравнения зависимости мольной теплоемкости оксида углерода от температуры. |
|
Ввод вектора действительных данных аргумента. |
|
|
|
Ввод вектора действительных данных значений. |
|
|
|
Ввод пользовательской векторной функции скалярного аргумента. |
|
|
|
Ввод вектора параметров линейной комбинациии функций пользователя, осуществляющей регрессию данных. |
|
|
|
|
|
Вывод результата счёта - коэффициенты уравнения |
|
Следовательно, искомое уравнение температурной зависимости теплоемкости оксида углерода: |
|
|
|
Мольная теплоемкость (Дж/мольK) углерода при 2000К. Разумеется, можно произвести расчет и при другой температуре. |
|
|
|
Сопоставим опытные |
|
|
|
|
|
|
|
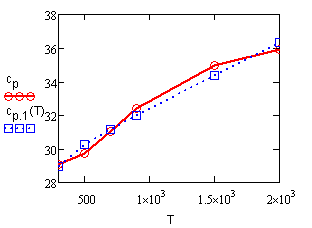
Рис. 17.1 иллюстрирует полученные результаты. |
|
|
|
Рис. 17.1.
Сопоставление опытных значений теплоемкости оксида углерода в зависимости от температуры. |
|
Задача 1.3.18. Диоксид углерода массой m
= 100г. находится при 273К
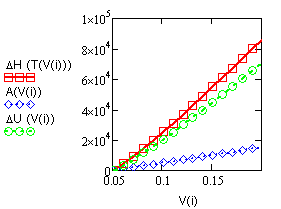
и давлении 1 атм. ( Определите теплоту Q,
работу A, изменение внутренней энергии - при изотермическом
расширении до объема - при изобарном расширении до того же объема, - при изохорном
нагревании до достижения давления 5 атм. ( Решение. Решение задачи основано на первом начале термодинамики, математическое выражение которого для процессов с бесконечно малыми изменениями состояния системы имеет вид: где В общем случае теплота и работа не являются
функциями состояния системы (они служат формами передачи энергии). Поэтому
обозначения В интегральной форме уравнение первого начала термодинамики (если совершается работа только против сил внешнего давления) будет иметь вид: Q = U + A, где Если исследуемая система является идеальным газом, внутренняя энергия которого зависит только от температуры
и состояние которого описывается уравнением Клапейрона-Менделеева где n - число молей газа, и совершается работа только против сил внешнего давления, то Теперь определим теплоту Q,
работу A, изменение внутренней энергии При изотермическом ( в интегральной форме примет вид При изотермическом процессе давление и объем связаны соотношением - ( считая, что при рассматривемых условиях газ подчиняется уравнению Менделеева - Клапейрона, то есть считая газ идеальным) и тогда после подстановки в предыдущее выражение
и, следовательно, |
|
Определимтеплотуиработу, которыевизотермическом процессеравны Q = А.
Исходныйобъём
Ипослеподстановкичисловыхзначений: |
|
|
|
Ввод массы газа, г. |
|
|
|
Ввод молярной массы газа, г/моль. |
|
|
|
Ввод значения газовой постоянной, Дж/мольК. |
|
Ввод температуры. |
|
|
|
|
|
Ввод давления, Па. |
|
|
|
Ввод соотношения,
определяющего объем газа ( |
|
Вывод результата -
объем газа ( |
|
|
|
Ввод соотношения,
определяющего количество теплоты при изотермическом расширении n молей идеальнoго
газа от объема |
|
|
|
Вывод результата -
теплота Q (Дж), которая выделяется ( и работа A, которая совершается) при изотермическом
расширении газа до объема 0.2 |
|
|
|
Проследим, как при постоянной температуре 273К влияет изменение объема на давление системы, теплоту
Q и работу A (которые в рассматриваемом случае
равны) при изотермическом расширении от начального объема |
|
Ввод массы m (г), молярной массы M ( г/моль), начального давления и температуры Т. Если вы хотите получить результат для другой массы - введите соответствующее значение m, для другого газа - значение его молярной массы M, при другой начальной температуре или давлении - соответствуюшие значения температуры ли давления. |
|
|
|
|
|
|
|
|
|
|
|
|
|
Ввод ранжированной переменной - объема. |
|
|
|
Ввод соотношения,
определяющего объем газа ( |
|
|
|
|
|
|
|
Вывод результата -
изменение давления в зависимости от объема газа ( |
|
|
|
Рис.18.1. Изменение давления диоксида углерода массы m = 100г. при 273К и давлении изотермическом расширении до объема |
|
Проследим теперь влияние объема диоксида
углерода массы m = 100г.
при его изотермическом при 273К
расширении до объема |
|
Ввод соотношения,
определяющего количество теплоты и работу при изотермическом расширении n молей идеальнoго
газа от объема |
|
|
|
|
|
Рис. 18.2. Влияние объема диоксида углерода массы m = 100г. при его изотермическом при 273К расширении до объема |
|
Теперь определим теплоту Q,
работу A, изменение внутренней энергии диоксида углерода массой m = 100г., который находится при 273К и давлении 1 атм. При изобарном процессе расширения газа уравнение имеет вид И в интегральной форме для n молей газа где Учтя, что при постоянном давлении и можно определить
температуру после расширения до объема Теперь, используя соотношение
определим
теплоту Разумеется, если в расчетах, представленных ниже, изменить массу газа, его молярную массу, начальный объем или начальную температуру, то можно получить результат для других условиях.
|
|
|
|
Ввод массы газа, г. |
|
|
|
Ввод молекулярной массы газа, г/моль. |
|
|
|
Ввод начальной температуры,К. |
|
|
|
Ввод начального
объема, |
|
|
|
Ввод конечного
объема, |
|
Ввод соотношения, определяющего температуру после расширения газа до объема V. |
|
|
|
Ввод соотношения, определяющего температурную зависимость теплоемкости, Дж/мольК, газа. |
|
|
|
Ввод соотношения, определяющего температурную зависимость изменения энтальпии n молей газа, Дж. |
|
|
|
Вывод результата
счёта - значение теплоты |
|
|
|
Теперь исследуем ,
как изменяется теплота Q ( а, значит, изменение
энтальпии H) при изобарном расширении диоксида углерода массы m = 100г при 273К и давлении 1 атм. до объема |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 18.2. Изменение
температуры при изобарном расширении диоксида углерода массы m = 100г при 273К и давлении 1 атм. до объема |
|
|
|
|
|
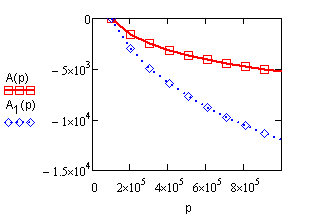
Рис.18.3.
Изменение теплоты Q ( а,
значит, изменение энтальпии H) при изобарном расширении
диоксида углерода массы m = 100г
при 273К и давлении 1 атм. до объема |
|
Теперь рассчитаем работу А: В случае изобарного процесса Тогда: |
|
|
|
Ввод соотношения, определяющего работу при изобарном расширении идеального газа. |
|
|
|
Вывод результата -
работа А (Дж) при изобарном (р = |
|
|
|
|
|
|
|
Рис.18.4.
Сравнение теплоты и работы (Дж) при изобарическом ( р = |
|
И тогда, поскольку можно определить
изменение внутренней энергии при изобарном расширении диоксида
углерода от объема или, подставив соотношения, выражающие теплоту и работу |
|
|
|
|
|
Ввод соотношения, определяющего изме- нение внутренней энергии при изобарном расширении идеального газа. |
|
Вывод результата - изменение внутренней
энергии при изобарном (р = Если вы хотите получить результат для
другой массы - введите соответствующее значение m,
для другого газа - значение его молярной массы M и
температурную зависимость теплоемкости |
|
|
|
|
|
|
|
|
|
Рис.18.4.
Сравнение теплоты, работы и изменения внутренней энергии |
|
Теперь определим теплоту Q,
работу A, изменение внутренней энергии При изохорном процессе dV=0 и в соответствии с работа А = 0 и в интегральной форме для n молей газа
или, поскольку |
|
Учтя, чтоприпостоянномобъеме и можноопределитьтемпературу, котораяустанавливаетсяпосле изохорногосжатиядодавленияр: |
|
|
|
Ввод числа молей исследуемого газа. |
|
|
|
Ввод начального |
|
|
|
|
|
Ввод начальной температуры,К. |
|
Ввод соотношения, определяющего температуру при изохорном нагревания газа до давления р. |
|
|
|
Вывод промежуточного результата - - температура при изохорном нагревания газа до давления р. |
|
|
|
Ввод соотношения, определяющего температурную зависимость теплоемкости, Дж/мольК, газа. |
|
|
|
Ввод соотношения, определяющего температурную зависимость изменения внутренней энергии n молей газа, Дж. при изохорном нагревании газа до давления р. |
|
|
|
Вывод результата - изменение внутренней
энергии при изохорном нагревании диоксида углерода массой m = 100г от давления Если вы хотите получить результат для
другой массы - введите соответствующее значение m,
для другого газа - значение его молярной массы M и
температурную зависимость теплоемкости |
|
|
|
Определительное уравнение термодинпмической функции состояния энтальпии имеет вид: H = U + pV В дифференциальной форме: При изохорном процессе dV = 0 и тогда
Тогда изменения энтальпии при изохорном
нагревании газа от давления
Теперь определим изменение энтальпии,
теплоту и работу при изохорном нагревании диоксида углерода массой m = 100г., который находится
при 273К и давлении 1 атм. ( |
|
|
|
|
|
Ввод соотношения, определяющего температуру при изохорном нагревания газа до давления р. |
|
|
|
Ввод соотношения, определяющего температурную зависимость изменения внутренней энергии n молей газа, Дж. при изохорном нагревании газа до давления р. |
|
|
|
|
|
Ввод соотношения,
определяющего температурную зависимость изменения энтальпии n молей газа, Дж. при изохорном нагревании газа от давления |
|
|
|
Вывод результата -
изменение энтальпии (Дж) при изохорном нагревании диоксида
углерода массой m = 100г
и 273К от давления Если вы хотите получить результат для
другой массы - введите соответствующее значение m,
для другого газа - значение его молярной массы M и
температурную зависимость теплоемкости |
|
|
|
Проследим, как изменяется теплота Q ( а, значит, изменение
внутренней энергии |
|
Ввод ранжированной переменной - давления р (Па) |
|
|
|
|
|
|
|
Ввод соотношения, определяющего температуру при изохорном нагревания газа до давления р. |
|
|
|
Ввод соотношения,
определяющего зависимость изменения внутренней энергии n
молей газа, Дж. при изохорном
нагревании газа от первоначального давления |
|
|
|
Ввод соотношения,
определяющего зависимость изменения энтальпии n
молей газа, Дж., при изохорном
нагревании газа от давления |
|
|
|
|
|
|
|
|
|
Рис. 18.5. Изменение температуры при изохорном нагревания газа до давления р. |
|
|
|
|
|
|
|
Рис. 18.6. Влияние
давления на изменение внутренней энергии |
|
В заключении приведем выражения, устанавливющие взаимосвязь работы и теплоты с изменениями внутренней энергии и энтальпии в изопроцессах с участием идеального газа. |
|
Уравнения для расчета работы, теплоты, изменения внутренней энергии и энтальпии в изопроцессах с участием моля идеального газа. ------------------------------------------------------------------------------------------------------------------------------------------------- Условия проведения Работа Теплота, внутренняя энергия, энтальпия процесса ------------------------------------------------------------------------------------------------------------------------------------------------- Изохорический A = 0 v = const. ------------------------------------------------------------------------------------------------------------------------------------------------- Изобарический p = const. ------------------------------------------------------------------------------------------------------------------------------------------------- Изотермический T = const. = 0 ------------------------------------------------------------------------------------------------------------------------------------------------- |
|
Как видно, теплоты изохорического и изобарического процессов равны, соответственно, изменению внутренней энергии и энтальпии. Поскольку оба эти процесса осуществляются в неизотермических условиях, то для нахождения теплоты необходимо знать, как внутренняя энергия и энтальпия зависят от температуры процесса, ф, значит, необходимо располагать данными о теплоемкости системы и ее зависимости от температуры процесса. |
|
Задача 1.3.19. Диоксид углерода массой m
= 100г. находится при 273К
и давлении 1 атм. ( Определите теплоту Q,
работу A, изменение внутренней энергии Решение. При адиабатном процессе Q = 0 и в соответствии с уравнением первого начала работа а, значит, при адиабатном процессе работа производится за счет убыли внутренней энергии системы и газ охлаждается. В свою очередь изменение внутреннй энергии
откуда работа при адиабатном расширении газа связана с понижением его температуры соотношением: При адиабатическом процессе одновременно изменяются и давление p, и температура Т, и объем V. Найдем связь между p, и V. При адиабатическом процессе (поскольку система не обменивается теплотой с окружающей средой) Если рассматриваемая система является идеальным газом, то: и, подставив давление р в предыдущее, соотношение: или Учтя, что следовательно или, приняв получим И тогда после интегрирования: или Подставив в последнее соотношение можно получить еще одно уравнение адиабатического процесса для идеальных газов:
|
|
Таким образом, при адиабатном сжатии теплота процесса Q = 0 и работа равна изменению внутренней энергии системы Найденные уравнения не являются строгими , поскольку при их выводе интегрирование проводилось в
допущении, что = уменьшается с ростом температуры. Адиабатное расширение - в отличие от изотермического - сопровождается охлаждением системы, и, наоборот, адиабатное сжатие - нагреванием. |
|
Теперь определим теплоту
Q, работу A, изменение внутренней энергии |
|
|
|
Ввод соотношений, определяющих температурную зависимость теплоемкости диоксида углерода при постоянном давлении и постоянном объеме. |
|
|
|
|
|
Ввод соотношения, определяющего ко- эффициент в уравнении адиабаты |
|
|
|
|
|
Ввод массы m (г) диоксида углерода и его молярной массы M (г/моль) |
|
|
|
|
|
|
|
Соотношение, определяющее число молей диоксида углерода, содержащееся в массе m. |
|
|
|
|
|
Ввод значений
начального |
|
|
|
Ввод начальной температуры. |
|
Ввод соотношения,
определяющего работу при адиабатном сжатии |
|
|
|
Вывод результата -
работа (Дж) при адиабатном сжатии до достижения давления |
|
|
|
Напомним, что при адиабатном процессе работа равна уменьшению внутреннец энергии A = - U Таким образом, в рссматриваемом случае U = |
|
Из определительного уравнения энтальпии H = U + pV следует, что при адиабатном процессе Конечный объем Тогда:
|
|
Ввод начальной температуры. |
|
|
|
Ввод соотношения, определяющего начальный объем, то
есть объем |
|
|
|
Ввод значения
изменения внутренней энергии (Дж) при адиабатном сжатии до достижения
давления |
|
|
|
Ввод соотношения, определяющего ко- эффициент в уравнении адиабаты |
|
|
|
|
|
Расчет и ввод значения коэффициент в уравнении адиабаты |
|
|
|
|
|
Ввод начального |
|
|
|
Ввод соотношения, определяющего изменение энтальрии при адиабатном процессе. |
|
|
|
Вывод
результата - изменение энтальпии (Дж) при адиабатном сжатии до достижения
давления 5 атм. |
|
|
|
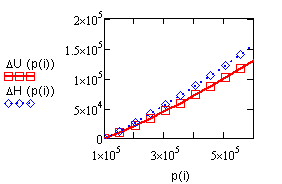
Сравним работу при проведении изотермического т адиабатного прцессов |
|
|
|
Ввод значения коэффициент в уравнении адиабаты |
|
|
|
|
|
Ввод соотношения,
определяющего работу при адиабатном сжатии |
|
|
|
Ввод соотношения,
определяющего работу при изотермическом сжатии |
|
|
|
Ввод значений давления (Па). |
|
|
|
|
|
Рис. 19.1 Работа
при адиабатном |
|
Задача 1.3.20. Определите работу испарения 3 молей метанола
при нормальной температуре кипения, то есть при нормальном внешнем давлении р
= Решение. Нормальная температура кипения Поскольку процесс протекает при постоянном давлении, работа может быть определена по соотношению где Конечный объем и объемом жидкого вещества - по сравнению с газообразным - в первом приближении можно пренебречь.Однако цена такого приближения остается не известной, поскольку не известно, насколько справедливо допущение, что газообразный метанол при нормальной температуре кипения 337.9К можно считать идеальным газом. Поэтому расчет объемов жидкого и газообразного метанола будем вести по формулам где
Тогда |
|
Ввод значения давления, Па. |
|
|
|
Ввод молярной массы метанола, кг/моль |
|
|
|
Ввод числа молей метанола |
|
|
|
Ввод плотности
жидкого |
|
|
|
|
|
Ввод соотношения, определяющего работу, Дж., при испарении жидкого вещества при постоянном давлении. |
|
|
|
Вывод результата - работа,Дж., при испарении 3 молей метанола при нормальной температуре кипения. |
|
|
|
Задача 1.3.21. |
|
|
|
|
|
|
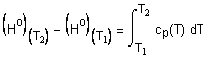
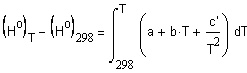
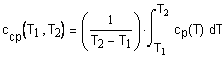
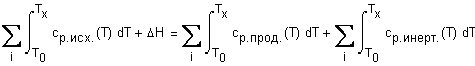
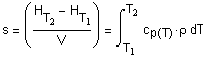

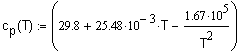
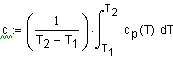
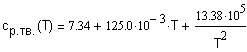
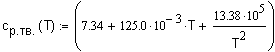
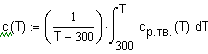



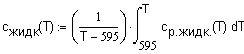




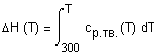 ,
,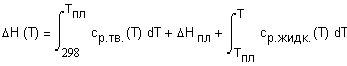 ,
,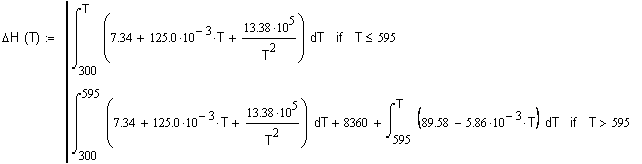


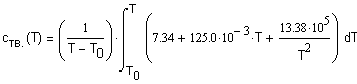

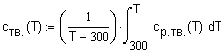
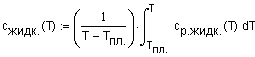


 ,
Дж/моль
,
Дж/моль 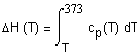 ,
,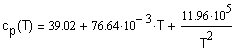 ,
Дж/
,
Дж/
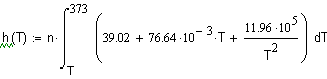



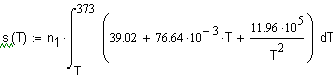

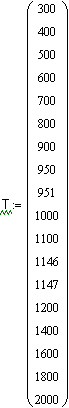
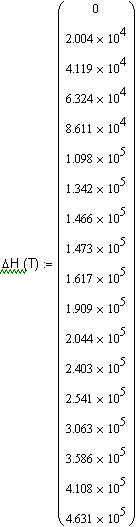
 ,
,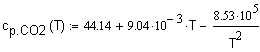
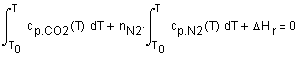

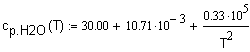
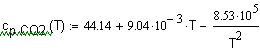
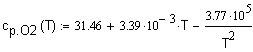
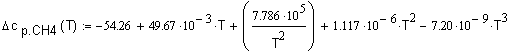
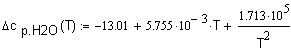
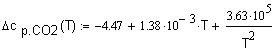
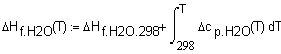
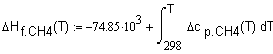
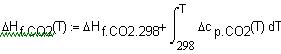
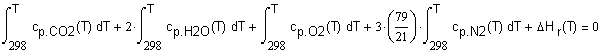
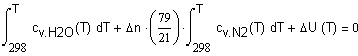 ,
,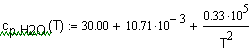
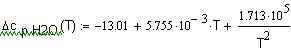
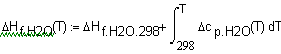
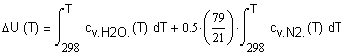 ,
,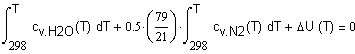



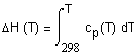
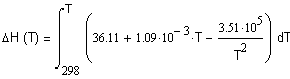
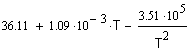



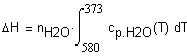
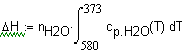
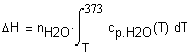
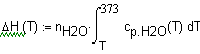



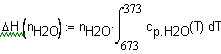

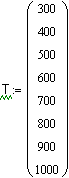
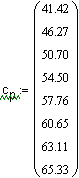
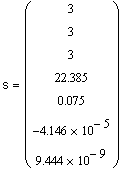

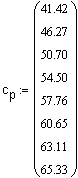

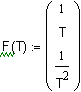
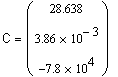
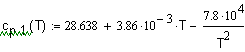
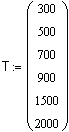
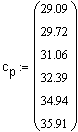

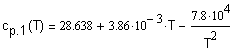
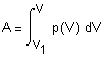


 ,
,