Глава 3. График на расчетном сайте (из книги В.Очкова >>>>>>>)
3.1.
Оцифровка графиков средствами Mathcad
3.2.
Оцифровка графиков внешними средствами
3.3.
Анимация и псевдоанимация
3.4. Построение семейства кривых в Mathcad
Как уже не раз отмечалось, очень часто в справочной и научно-технической литературе функциональные зависимости даются не формулами, а графиками. Причем сами функциональные зависимости, по которым строились графики, не приводятся. Нет и таблиц, по которым построены графики. На рис. 3.1 в качестве примера представлен один из таких графиков, отражающий влияние скорости воды и ее температуры на удельное гидравлическое сопротивление в некоем фильтрующем материале, через который воду прокачивают. Рисунок взят из справочной документации одной известной фирмы, поставляющей водоочистное оборудование.
Подобные графики приводятся не только для качественного описания тех или иных явлений (гидравлическое сопротивление растет при увеличении скорости и падает при повышении температуры, если говорить о рис. 3.1), но и для их количественной оценки – для расчетов. В упомянутой фирменной документации описан расчет этого гидравлического сопротивления по методике «вождения пальцем по графику»: отложите по оси абсцисс значение скорости (первый аргумент), поднимитесь до нужной температуры или мысленно проведите недостающую кривую (изотерму – второй аргумент), поверните налево и считайте ответ (значение функции двух аргументов) на оси ординат.
В справочниках встречаются также и более сложные графические зависимости – разного рода номограммы с инструкциями такого рода: отложите значение первого аргумента на первой шкале, а второго – на второй; соедините точки прямой линией и на средней шкале считайте ответ. По адресу http://twt.mpei.ac.ru/MAS/Worksheets/Boiler/Th_C_B_Nom_2.mcd хранится образец такой номограммы, моделирующей функцию уже трех аргументов – см. рис. 3.2. Изменение в полях ввода скажется на номограмме после нажатия кнопки Recalculate (Пересчитать). Номограмма, показанная на рис. 3.2, – это фактически два Х-Y-графика, пристыкованных друг к другу так, чтобы горизонтальная линия первой (правой) функции плавно переходила в горизонтальную линию аргумента второй (левой) функции.
В номограммах (а на них выросло целое поколение инженеров) «тонет» физика задачи – ее качественная оценка, зато повышается точность таких «графических» расчетов. Выпускались даже нехитрые механические устройства типа логарифмической линейки с вшитыми в них алгоритмами. Такие устройства были особо популярны у штурманов, прокладывающих маршруты морских и воздушных судов до наступления эры бортовых компьютеров и глобальных систем позиционирования. Сейчас что-то подобное можно купить в газетных киосках – совместил на двух дисках свой вес и рост и узнал, пора ли переходить на диету...
Но для современных расчетов с использованием компьютеров или просто калькуляторов более подходят не графики и номограммы, а формулы (см. гл. 2), которые часто не приводятся в технической литературе по ряду причин.
Во-первых, формулы не даются из благих намерений освободить читателя от расчетов. Тем более это зачастую и не расчет в привычном понимании этого слова, а некая оценка, прикидка того или иного параметра. В той же документации, откуда взят рис. 3.1, рекомендовано при выборе насоса для фильтра (а его напор – это произведение удельного гидравлического сопротивления на высоту фильтрующего материала) увеличить расчетное гидравлическое сопротивление на 10–20% (так называемый инженерный запас, нивелирующий помимо прочего и ошибки считывания «пальцем» чисел с графика). «Расчетные» графики – это атавизм тех времен, когда даже простейший расчет был проблемой для инженера. Теперь же рабочий стол инженера оборудован ну если не компьютером, то как минимум программируемым калькулятором и проблем с расчетами не должно быть. Но «расчетные» графики без соответствующей формулы продолжают появляться даже во вновь издаваемых справочниках. Иногда в справочнике можно видеть некий гибрид графика и формулы. На рис. 3.3 показан пример такого расчета, когда через график определяется зависимость функции (удельное гидравлическое сопротивление некоего фильтрующего материала) от первого аргумента (от скорости потока через фильтр), а по эмпирической формуле – от второго аргумента – от темрературы.
Во-вторых, нередко никакой формулы не было, и нет, так как на графиках даны результаты некой графической обработки опытных точек. Кривые, показанные на рис. 3.1, получены после испытания фильтрующего материала на специальном стенде, где есть возможность менять скорость потока, а также температуру воды и замерять перепады давления. Полученные экспериментальные точки были проставлены на графике, вблизи них неким лекалом или статистической обработкой (см. гл. 4) были проведены линии, а затем сами точки стерты. В научной же (не технической) литературе считается хорошим тоном оставлять на графике экспериментальные точки и показывать различного рода доверительные интервалы. В последнее время получает распространение практика ссылок из научных статей на сайт, где хранятся первичные протоколы опытов, по которым читатель (оппонент) может не только проверить выводы автора, но и дать свою трактовку результатов. Можно идти дальше и делать ссылки на программу с расчетом по этому графику. На бумаге (в справочной документации – см. рис. 3.1) видна качественная картина явления, а на сайте, поддерживающего эту документацию, прописан соответствующий расчет – см. рис. 4.5 в гл. 4 ниже. Для этого можно:
- попытаться связаться с автором и попросить его дать формулу, если она, конечно, была и по ней был построен сам график график;
- вывести самому нужную формулу, опираясь на «физику»
задачи; в нашем случае, например, сопротивление фильтрующего материала
может зависеть от скорости фильтруемой жидкости (воды) в степени близкой к
квадратной, а сами кривые выходят из начала координат: у
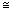 k·х2 –
здесь достаточно установить значение коэффициента k;
k·х2 –
здесь достаточно установить значение коэффициента k; - подойти к задаче несколько формально (феноменологически) – провести интерполяцию или аппроксимацию по точкам с опорой на стандартные функции –полином некой степени, например.
В данной главе в первую очередь будет рассказано о том, как график из справочника можно «оцифровать» – получить массив данных (векторы и матрицы), который затем можно будет «оживить» приемами, которые будут описаны в гл. 4.
График, конечно, можно «оцифровать» докомпьютерными (безкомпьютерными) средствами – взять в руки линейку и калькулятор и вручную составить таблицу значений точек на графике. Но современные аппаратные и программные средства компьютеров позволяют автоматизировать эту работу.
3.1. Оцифровка графиков средствами Mathcad
Первый шаг на пути оцифровки «бумажного» графика – это его сканирование, получение его электронного растрового изображения – файла. Такой файл (изображение) требует минимальной последующей доработки – поворота при необходимости изображения с помощью какого-нибудь графического редактора так, чтобы ось ординат была строго горизонтальна, а ось абсцисс, соответственно, вертикальна. Но часто и этого не требуется, если страница справочника с графиком была установлена в сканере аккуратно без перекосов. Для этого иногда приходиться, увы, разрывать книги на отдельные страницы и ровно обрезать их края. С другой стороны, если не книгу (страницу книги) несут к сканеру, а сам сканер (ручной сканер) несут к книге и проводят им по раскрытой странице, то может потребоваться дальнейшая обработка – разворот графика и т.д. На рис. 3.4 показан график, отсканированный из справочника «Физические величины» (М.: Энергоатомиздат, 1991) и показывающий влияние температуры и солености морской воды на скорость звука в ней. Далее будет рассказано, как такой и другие подобные графики можно «оцифровать», будут раскрыты некоторые приемы такой работы в среде Mathcad.
На рис. 3.5 показано, как в Mathcad-документ командой Insert Picture
из панели инструментов Matrix вставлен рисунок одной кривой
графика, показанного на рис. 3.4. Для этого
график предварительно был отредактирован компьютерным ластиком – из него
было убрано все лишнее, а сама линия была сохранена на диске файлом с именем CC_Plot.jpg.
Оператор READBMP (см. рис. 3.5) формирует матрицу М, хранящую цвета точек (оттенки серого)
растрового изображения в кодировке от 0 (черный цвет) до 255 (белый). Здесь
становится понятен смысл слова «растровое изображение» – некое мозаичное
изображение, формируемое отдельными точками (квадратиками). На
рис. 3.5 показан фрагмент этой
матрицы («мозаики») в диапазоне столбцов от нулевого до шестого и строк от
302-й до 312-й (левый нижний угол матрицы М,
левый край кривой). Далее в программе перебором столбцов (цикл с
параметром i) и строк (параметр j) ведется заполнение
векторов Х и У координатами точек с черным цветом
(код со значением
На рис. 3.6 показана статистическая
обработка векторов Х и
У, значения которых считываются с
диска, а затем подвергаются статистической обработке. Далее в этой и
последующей четвертой главе будут задействованы некоторые специальные (статистические)
встроенные функции Mathcad.
Их описание можно найти в Интернет в виде гл. 16 книги Гурского Д.А. и Турбиной
Е.С. Гурского и Турбиной «Вычисления в Mathcad 12» (Издательство Питер,
Проведенная статистическая обработка позволила получить функцию у(х), по которой можно считать (у(250)) = 240.586, например) и строить график – см. на рис. 3.6 увеличенный фрагмент кривой, «пронизывающей» точки.
Другой подход к оцифровке графика показан на рис. 3.7 и рис. 3.8. Графики в настоящее время все чаще и чаще можно найти не только на «бумаге» справочников, но и в электронном виде в файлах, хранящихся и в Интернет. Так, на рис. 3.7 показан открытый с помощью Adoble Reader (программы, свободно распространяемой в Интернет и служащей для открытия так называемых pdf-документов – документов, созданных в среде текстового процессора Adobe Acrobat – см. www.adobe.com) график некой зависимости. Этот график можно перенести в среду, например, графического редактора Paint, входящего в состав операционной системы Windows, там убрать лишнее, отметить цветными крапинками узловые точки на кривой (у нас на рис. 3.8 – это одиннадцать точек пересечения кривой с вертикальной сеткой) и открыть этот графический файл в среде Mathcad. На рис. 3.8 в матрице М ищутся уже не черные точки с кодом 0 как на рис. 3.5, а точки с кодом 76, фиксирующим цвет, которым были отмечены узловые точки графика.
3.2. Оцифровка графиков внешними средствами
С графическими файлами, хранящими отсканированные (рис. 3.4) или скопированные из электронных документов (рис. 3.7) графики, можно, а в ряде случаев и целесообразно поступить иначе, чем показано на рис. 3.5 и рис. 3.8. Такой файл можно открыть в среде какого-либо пакета, специально созданного для оцифровки графиков. На рис. 3.9 показана работа одного из таких пакетов, написанного В. Писковым и который можно скачать из Сети по адресу http://twt.mpei.ac.ru/TTHB/5/3/AIGraph.exe. На рис. 3.9 зафиксирована работа с программой с данной программой. Если подвести курсор мыши к нужной точке графика и щелкнуть по левой кнопки мыши, то в полях Х и Y (см. правый край рис. 3.9) появятся координаты данной точки (режим «Определить координаты»). Перед такой работой через режим «Контрольные точки» (см. правый верхний угол на рис. 3.9) необходимо оттарировать график – отметить две любые точки на графике (к качестве таких точек обычно выбирают находящиеся на противоположных концах диагонали графика) и указать их координаты. В нашем случае это будут X=0 Y=1400 и X=30 Y=1540 – две отдаленные друг от друга точки пересечения линии сетки графика. После этого при работе в режиме «Определить координаты» в полях Х и Y будут фиксироваться истинные координаты точек на графике, которые затем можно перенести в вектора и матрицы Mathcad-документа. На рис. 3.5 (см. выше) векторы Х и Y хранили не координаты точек на графике, а значение индексов матрицы М. На другом рисунке выше, на рис. 3.8 эти значения были подправлены через операторы Х =100 Х/378 и У = 0.24·Y/183+1. В программу, отображенную на рис. 3.9, заложена также технология, когда пользователь проводит курсором мыши по выбранной кривой графика, нажав при этом на левую кнопку мыши. В этом случае в полях X и Y автоматически генерируются соответствующие вектора значений координат точек графика с заданным заранее шагом. Более подробная инструкция по работе с программой, отображенной на рис. 3.9, находится в пакете.
Координаты точек рисунка без расчета истинных значений координат точек графика можно получить, работая с графическим редактором Paint Brush (см. рис. 3.9a), входящим в состав Widows.
Забегая вперед – в гл. 4, покажем, как идеи, заложенные в рис. 3.4 – 3.9, доводятся до логического завершения средствами Mathcad. На рис. 3.10 показана страница Интернета с «ожившим» графиком, показывающим влияния температуры и солености воды на скорость звука в ней. Такой «оцифрованный» и открытый в Интернет график можно использовать и для счета (по заданным посетителем сайта значениям температуры строится вертикальная линия, а по значению солености воды – недостающая кривая: искомое значение фиксируется горизонтальной линией и выводится числами в разных единицах скорости), но и просто для более аккуратного «внешнего вида» – сравните рис. 3.4 и рис. 3.10. Более того, рис. 3.10 уже не растровый, а фактически векторный, что позволяет помимо прочего менять его размер без потери качества, что очень удобно при подготовки к публикации графиков как в Сети, так и на «бумаге». Кроме того, такой график легко перестроить – поменять местами два его аргумента и увидеть новое семейство кривых – см. рис. 3.11, которые, в частности, показывают, что скорость звука в воде зависит от солености почти линейно, чего не видно при анализе другого отображения данной зависимости, показанного на рис. 3.10.
3.3. Анимация и псевдоанимация
Суть анимации, создаваемой с помощью Mathcad и других программ, часто объясняют на примере старой детской игрушки. Берется блокнот, на каждой страничке которого рисуется некий сюжет (человечек в определенной позе) так, чтобы картинка плавно изменялась от страницы к странице, создавая некое действие (человек поднимает руку, например). Если такой разрисованный блокнот просто перелистывать постранично, то никакого анимационного эффекта не наблюдается. Но если его, зажав, перелистывать быстро, отпуская пальцем, то можно увидеть анимацию, мультфильм.
В среде Mathcad можно вручную менять значения какой-либо переменной и видеть, как, например, меняется кривая на графике. Но быстро, так, чтобы получилась анимация, этого сделать невозможно: анимация получается при смене не менее 10 кадров в секунду. Поэтому в Mathcad введены специальные средства анимации, включающие в себя системную переменную FRAME (счетчик кадров) и две команды Record... (Запись...) и Playback... (Воспроизведение...) из меню Tools | Animation (Сервис | Анимация).
На рис. 3.12 показаны этапы создания в среде Mathcad анимационного клипа в не совсем обычном ракурсе – для генерации своеобразного exe-программы, выполнимого файла – расчета, который может работать без самой программы Mathcad. Для этого в Mathcad-документ вставлена функция с именем CH2SO4, возвращающая концентрацию раствора серной кислоты в зависимости от его плотности (ведется сплайн-интерполяция по табличным значениям, хранящимся в матрице M – тема гл. 4). Переменной FRAME пользователь может задавать целочисленные значения в диапазоне от 0 до 100, что меняет значение переменной ρ (плотность раствора серной кислоты) от 1 до 1.8 через выражение 1+ FRAME∙0.008 и что, в свою очередь, изменяет значение искомой переменной С (концентрация раствора серной кислоты). При создании анимации оператор FRAME := глушится (переводится в комментарий, о чем свидетельствует черный квадратик справа от оператора – см. гл.1), а управление этой переменной передается самой программе Mathcad – диалоговому окну Record Animation (Запись анимации), где отмечается, от (From) какого и до (To) какого целочисленного значения должно меняться значение системной переменной FRAME и, какая будет частота показа кадров (At – кадры в секунду). Размер же самих кадров определяется протяжкой (выбором) мышью прямоугольной области на экране дисплея. На рис. 3.12 она показана пунктирной линией, охватывающей два оператора вывода ρ = и С =. Теперь после нажатия кнопки Animate (Анимация) пакет Mathcad будет сам менять значение переменной FRAME в отмеченном диапазоне (0-100 с шагом 1), а через нее значения переменных ρ и С. и записывать полученные кадры анимации (рисовать на страничках блокнота) для их будущего быстрого показа (пролистывание блокнота). Полученный анимационный клип (см. диалоговое окно Play Animation на рис. 3.12) можно записать на диск и запускать без пакета Mathcad (своеобразный exe-файл, о котором говорилось выше).Бегунком (см. диалоговое окно Play Animation на рис. 3.12) можно установить значение переменной ρ (или С) и считать значение переменной С (или ρ – обратная задача).
Но, как правило, анимируют не изменяющие числа (см. рис. 3.12), а графики. Так на рис. 3.13 показано окно анимации движения трех планет под действием закона всемирного тяготения, моделирование которого было отображено на рис. 2.27 в гл.2.
Пакет Mathcad
Application/Calculation
Server (MAS – его описание см. в гл. 1) позволяет публиковать
Mathcad-документы в Интернет не только для просмотра (это делалось уже давно),
но и для счета по ним. Пользователь (но уже не пакета Mathcad, а браузера
Интернета, а в этом и состоит главное преимущество технологии MAS) может
изменить в открытом в Интернет документе исходные данные и получить новый
ответ – числа, графики и
В инструкции разработчику приложений для MAS сказано, что кнопка Submit бесполезна в "нормальных" Mathcad-документах, а необходима только для WebSheets – Mathcad-документов, подготовленных для публикации в Интернете посредством MAS. Эту информацию вставили в диалоговое окно Submit Button Properties (Свойства кнопки Submit). На рис. 3.14 она обведена и гласит: "Кнопка Submit бесполезна в несетевом Mathcad-документе". Но эта информация дезориентирует пользователей Mathcad и отсекает от них довольно интересный инструмент.
Во-первых, без нажатия кнопки Submit можно обойтись в WebSheets. Кнопку Submit нажимают после того, как в Mathcad-документе сделаны нужные изменения и их необходимо передать (от англ. to submit – передавать, представлять на рассмотрение, на экспертизу) на сервер для расчета в среде Mathcad, установленной на этом сервере. Но можно так отформатировать "сетевые" элементы интерфейса, что изменение в них и.или нажатие клавиши <Enter> будет сигналом для посылки данных на сервер и без нажатия на кнопку Submit.
Здесь просматривается прямая аналогия с режимом ручного пересчета в среде Mathcad (Excel, Word, BASIC, Pascal и т. д.). Кнопку Submit можно сравнить с клавишей <F9>, которую нажимают после того, как в WorkSheet (в Mathcad-документе, открытом в среде Mathcad, а не в Интернет) сделаны нужные изменения и необходимо, чтобы был выполнен соответствующий пересчет.
Во-вторых,
кнопка Submit
может быть очень полезна не только в WebSheets, но и в WorkSheets – в
традиционных (несетевых) Mathcad-документах. Дело в том, что нажатие этой
кнопки увеличивает на единицу значение переменной, связанной с кнопкой Submit. После открытия Mathcad-документа в сетевом
или несетевом режиме значение этой переменной равно единице. Данная переменная
является своеобразным счетчиком количества нажатий кнопки Submit,
Здесь опять же можно провести аналогию, но уже не с клавишей <F9>, а с переменной FRAME, управляющей анимацией (см. выше). Теперь в среде Mathcad легко создавать некую псевдоанимацию, кадры которой в прямом и обратном порядке можно менять, нажимая кнопки Submit.
В среде Internet Explorer такую псевдоанимацию можно ускорить – превратить в почти настоящую анимацию за счет буфера браузера (см. рис. 3.16, где надписями подчеркнуты кнопки "Назад" и "Вперед", нажимая которые после наполнения буфера браузера можно показывать анимацию без обращения к MAS).
На рис. 3.17 показана пошаговая псевдоанимация термодинамического цикла Отто с зацикливанием, если так можно выразиться, самого цикла: посетитель данного сайта нажимает кнопки браузера «Вперед» и «Назад» и видит не только параметры цикла в узловых точках, но и ход поршня в двигателе внутреннего сгорания. Предварительно пользователь сайта нажимает соответствующие кнопки у группы радиокнопок «Выбери точку», подгружая тем самым в расчет ту или иную картинку, отображающую фазу работы тепловой машины.
3.4. Построение семейства кривых в Mathcad
Функции двух независимых аргументов (переменных) f(x, y) в среде математических пакетов и, в частности, в среде Mathcad можно отображать средствами трехмерной графики – поверхностями. Но в справочной литературе трехмерные графики используются редко. С трехмерными графиками, спроецированными на плоскость страницы справочника или экрана дисплея, трудно работать – наблюдать зависимости, оценивать значения и т.д. Функции двух аргументов в справочной литературе, как правило, отображаются семейством кривых (см. рис. 3.1, 3.4, 3.9, 3.10 и 3.11 выше), на которых четко видимы те или иные зависимости (наклон кривых, например) и по которым при необходимости можно провести оценку значения самой функции в той или иной точке.
В среде Mathcad на одном декартовом графике (X-Y Plot) можно построить до 16 кривых. На рис. 3.18 показано, как строятся такие кривые: один (первый) аргумент – функции y является формальным параметром (x) и продублирован на оси ординат, а второй аргумент – это константа явно прописанная (0.1, 0.5 и 10), либо заданная через переменную (e). Можно отметить следующие недостатки данного способа построения семейства кривых:
1. Число выводимых на график кривых задается явно через форматирование самого графика – изменение списка функций оси абсцисс. Но это действие заблокировано при открытии Mathcad-документа через технологию MAS.
2. Число кривых на графике не может быть больше 16 или 32 (см. выше).
3. При большом числе кривых (записей у оси абсцисс) сам график становится слишком высоким и его вертикальный размер нельзя уменьшить протяжкой (тут можно сказать «утяжкой») графика.
Альтернативная технология построения семейства кривых, которая будет описана ниже, основана на генерации двух векторов y(x)[2] и x, хранящих координаты кривых.
На рис. 3.19 показано, как пользователь вводит в текстовое окошко функцию двух аргументов[3], далее в другом текстовом окошке списком через запятую указывает, при каких значениях переменной а должны быть построены кривые семейства в диапазоне изменения первого аргумента х от х1 до х2. Тут могут быть и не текстовые окошки, а простые операторы присваивания (задания) функции у(х, а), значений вектора а и констант х1 и х2. Если же задействованы текстовые окошки (документ готовится к публикации в Сети по технологии MAS), то в ход идет функция Str2Math, переводящая текст (Str) в математическую (Math) конструкцию: функцию пользователя, вектор, скаляр…
На рис. 3.20 показаны операторы, скрытые на рис. 3.19. Они формируют два вектора х и у(х), описанные выше, с помощью двух циклов с параметром. В первом, внешнем цикле ведется перебор вектора а, а во втором цикле, вложенном в первый – значений х, заданных диапазоном х1-х2 и числом точек в нем n. При этом перебор значений х во вложенном цикле ведется по-разному в зависимости от номера кривой в семействе: от х1 к х2 при четных значениях номера кривой и от в обратном направлении от х2 к х1 – при нечетных значениях. Этот прием позволяет соединить конечные точки на графиках линиями так, чтобы само семейство кривых не перечеркивалось диагональными линиями, соединяющими последнюю точку предыдущей кривой с первой точкой последующей. На нашем графике (рис. 3.19) эти линии стали горизонтальными и за счет наложения на рамку графика – невидимыми. Другой (традиционный) способ делать невидимыми соединительные диагональные линии – это увеличение числа точек (значения переменной n на рис. 3.20) и форматирование графика не линиями, как это сделано на рис. 3.20, а точками, сливающимися в линию, если сама функция у(х, а) меняется от х не слишком резко. Но этого нельзя сказать о нашем случае (рис. 3.21), когда строится зависимость энтальпии воды и водяного пара от давления при разных значениях температуры (семейство изотерм), где в докритической области функция wspHPT скачком меняется от области пара на линии насыщения к области воды на линии насыщения через область влажного пара.
Еще одна особенность программы, показанной на рис. 3.21 состоит в следующем. Векторы у(х) и х заполняются в отдельных циклах for… for…, хотя, казалось бы, в целях ускорения работы программы эту операцию нужно делать в одном цикле. Но дело тут в том, что эти два вектора могут быть и размерными (а это как раз наш случай – см. рис. 3.19, где аргумент х имеет размерность давления, а сама функция у(х, а) – удельной энтальпии). Mathcad-программа не может возвратить два вектора или два скаляра с разной размерностью.
Кстати о размерности. На рис. 3.20 значение удельной энтальпии в заданной точке (р = 200 atm и t = 800 K) выдано не в Дж/кг, а в м2/с2, т.е. упрощено до предела – отформатировано соответствующим образом. Это связано с тем, что тут могут выдаваться различные значения с разными единицами измерения в зависимости от вида введенной функции в первом текстовом окне на рис. 3.20. Из-за этого нельзя заранее подставить нужные («жесткие) единицы измерения в последний операнд оператора вывода численного значения ■ = ■ ■, предназначенного для корректировки единиц измерения выводимой величины. Кстати, подобное не вполне законное (логичное) упрощение единиц мы и сами часто делаем, не замечая этого. Конкретный пример. Единицей теплопроводности должна быть единица W m/(m2 K), а не W/(m K). Метры тут сокращать нельзя, так как ими измеряются разные величины – длина (m) и площадь (m2).
На рис. 3.22 показано, как можно у семейства кривых поменять переменную у оси x и построить уже не семейство изотерм, а семейство изобар.
[2] Это не функция у от x, а переменная с именем у(х), которая в среде Mathcad создается через аккорд Ctrl-Shift-k, глушащего ввод спецсимволов ”(“ , “)” и др. Можно, конечно, данному вектору дать и более традиционное, простое имя – y, например. Но имя у(х) более информативно.
[3] У нас тут задействована функция wspHPT из пакета WaterSteamPro (www.wsp.ru – см. гл. 5), возвращающая энтальпию (H) воды или водяного пара в зависимости от давления (Р) и температуры (Т – см. комментарий, который можно ввести в текстовое окошко после точки с запятой). Но тут может быть любая другая функция или выражение с переменными х и а.