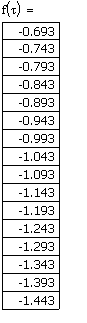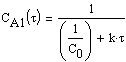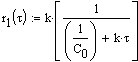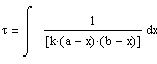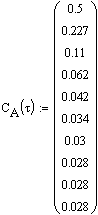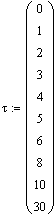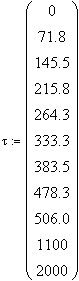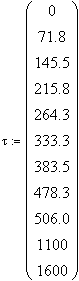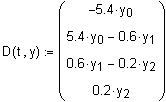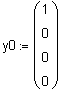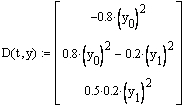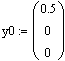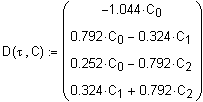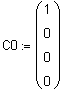Мультимедийный курс «
Кинетика химических реакций»
Совместный проект кафедры Химии и электрохимической энергетики и кафедры Технологии воды и топлива Московского энергетического института (ТУ)
Курс содержит разделы:
Конспект лекций «Кинетика химических реакций»
Обучающую программу «Зависимость скорости реакции от концентрации и температуры»
Решебник « Расчетные задачи химической кинетики»
1.
ОБЩИЕ ЗАКОНОМЕРНОСТИ ХИМИЧЕСКОЙ КИНЕТИКИ
1.2. Влияние концентрации на скорость реакции
1.3.
Молекулярность и порядок реакции
1.7.
Методы определения порядка реакции
2.1.
Кинетика обратимых реакций
3.
ВЛИЯНИЕ ТЕМПЕРАТУРЫ НА СКОРОСТЬ
3.2.
Связь энергии активации с тепловым эффектом реакции
3.3.
Связь между скоростью реакции и равновесием
4.
КИНЕТИКА ГЕТЕРОГЕННЫХ РЕАКЦИЙ
4.2.
Макрокинетика. Внешнедиффузионная область
4.3.
Макрокинетика. Внутридиффузионное торможение
МОСКОВСКИЙ ордена ЛЕНИНА ЭНЕРГЕТИЧЕСКИЙ ИНСТИТУТ
ВВЕДЕНИЕ
Уровень
развития цивилизации (разумеется, это немного
односторонний подход) можно охарактеризовать количеством производимой
энергии. И тут оказывается, что около 90% всей энергии, производимой
человечеством, получается за счёт химической энергии топлива. Остальное
приходится на гидроэлектростанции, атомные станции и т.д.
Поэтому изучение скорости протекания
химических процессов (а это и составляет задачу кинетики) чрезвычайно важно.
Химические реакции могут протекать с самыми
различными скоростями – от взрывных до очень медленных, протекающих в течение
многих месяцев и лет. Даже одна и та же реакция, протекающая на различных
катализаторах, может иметь скорости, различающиеся во много раз.
В некоторых случаях необходимо увеличить
скорость реакции, в других наоборот, уменьшить. Таких примеров можно привести
множество.
Для рационального проведения химических
реакций необходимо уметь управлять ими, знать зависимости скорости от различных
параметров.
1. ОБЩИЕ ЗАКОНОМЕРНОСТИ ХИМИЧЕСКОЙ КИНЕТИКИ
1.1. Скорость реакции
Химическая
кинетика – наука о скоростях и закономерно-стях протекания химических процессов во времени.
Химическая
кинетика изучает механизм протекания процесса, т.е. те промежуточные стадии,
через которые система переходит из начального в конечное состояние, скорости
этих стадий и факторы, влияющие на их скорость.
Изучить кинетику реакции – значит показать,
как реально протекает исследуемая реакция, её механизм, получить зависимость,
связывающую скорость реакции с факторами, влияющими на неё.
Различают два типа химических реакций:
гомогенные и гетерогенные.
К гомогенным относятся реакции, у которых и
исходные вещества и продукты реакции находятся в одной фазе. Взаимодействие
веществ в таких реакциях происходит по всему объёму.
К гетерогенным реакциям относят реакции,
протекающие на границе раздела фаз.
Пусть протекает реакция
![]() (1.1)
(1.1)
где
a1,
a2,
ai, b1, b2, bj – стехиометрические
коэффициенты.
Скорость реакции по i–му веществу в гомогенной
системе определяется как количество i-го вещества, образующееся
(или реагирующее) в единице реакционного объёма в единицу времени:
![]() (1.2)
(1.2)
где
V – объём реакционной зоны;
Ni – количество i–го
вещества.
Если реакция протекает изохорически, т.е.
объём во время реакции не меняется, то, поскольку концентрация и объём связаны
соотношением
![]() ,
,
скорость реакции
![]()
Ранее мы определили
скорость химической реакции как изменение числа молей реагирующих веществ в
единицу времени в единице объема, т. е.
![]()
где ![]() — изменение
числа молей одного из исходных веществ за время
— изменение
числа молей одного из исходных веществ за время ![]() .
.
Таким образом, определяется средняя скорость реакции для заданного
интервала времени.
Если объем в процессе реакции постоянен, то
![]()
где ![]() — изменение концентрации.
— изменение концентрации.
Тогда
![]() или
или 
(скорость всегда положительна, а ![]() может быть больше или
меньше нуля в зависимости от того, концентрацию исходного вещества или продукта
мы рассматриваем).
может быть больше или
меньше нуля в зависимости от того, концентрацию исходного вещества или продукта
мы рассматриваем).
Если интервал времени
![]() , то мы получим истинную скорость реакции r в данный момент времени, т. е.
, то мы получим истинную скорость реакции r в данный момент времени, т. е.
![]()
или
![]() (1.3)
(1.3)
Размерность
скорости: моль/(л·с).
Не только знак, но и абсолютное значение
скорости зависит от того, по какому из участников реакции она измерена.
Так, например, для реакции
![]()
скорость,
с которой уменьшается концентрация водорода во время процесса в три раза больше
скорости убывания концентрации азота, и в полтора раза выше скорости
возрастания концентрации аммиака.
Следовательно, для реакции
![]()
скорости по компонентам реакции будут связаны
соотношением
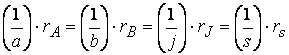
Экспериментально установлено, что скорость
реакции зависит от природы реагирующих
веществ, их концентрации (или давления), температуры, т.е.
![]()
Раскрытие
этой зависимости и составляет одну из задач кинетики.
1.2.
Влияние концентрации на скорость реакции
Подход к выяснению зависимости скорости реакции от
концентрации реагирующих веществ можно иллюстрировать следующим положением
теории вероятностей: вероятность одновременного осуществления независимых
событий равна произведению вероятностей каждого из них.
Для того чтобы произошло химическое взаимодействие,
например, реакция
A+B→продукты,
Необходимо, но не достаточно, столкновение
реагирующих молекул А и В, т.е. одновременное нахождение их в определённой
точке реакционного пространства.
Вероятность (ω) нахождения молекулы для
каждого из веществ прямо пропорциональна количеству молекул в единице объёма, т.е. его концентрации:
![]() ,
, ![]() .
.
Тогда вероятность того, что обе молекулы
будут одновременно находиться в одной точке пространства, т.е. что они столкнутся,
равна
![]()
Но не все столкновения
приведут к реакции, а лишь их некоторая доля α, величина которой зависит от температуры и природы
веществ, поэтому скорость реакции
A + B → продукты
равна
![]()
или
![]()
Постоянную k, не зависящую от концентрации и зависящую только от температуры и природы реагирующих веществ, называют константой скорости.
Численное значение k выражает скорость реакции,
когда концентрации реагирующих веществ равны 1 моль/л.
Обобщим сказанное.
Пусть протекает химическая реакция:
aA + bB + … → продукты.
Тогда
зависимость скорости реакции от концентрации можно выразить соотношением
![]() (1.4)
(1.4)
Полученное
выражение называют законом действия масс.
1.3. Молекулярность и порядок реакции
Число молекул, вступающих в
реакцию, определяют молекулярность реакции.
Так, если в реакцию вступает одна молекула,
то такая реакция называется молекулярной реакцией. Если в реакции участвуют две
молекулы (безразлично, одинаковые или нет), то такая реакция называется
бимолекулярной. Встречаются также тримолекулярные реакции.
Реакции более высокой степени молекулярности
крайне редки из–за малой вероятности одновременного столкновения большого числа
молекул.
Поэтому большинство реакций протекают в
несколько элементарных, простых стадий, в которых участвует небольшое число
молекул.
Определить такие стадии – значит определить
механизм, или путь реакции.
Скорость всей реакции определяется скоростью
её наиболее медленной стадии, которая и определяет механизм.
Поэтому закон действующих масс справедлив
только для таких элементарных стадий.
Молекулярность реакции легко определить в
случае простых реакций, протекающих в одну стадию. В большинстве же случаев
довольно трудно найти молекулярность реакции.
Поэтому вводится понятие порядка реакции,
который можно найти из кинетических уравнений, полученных экспериментально.
Порядок реакции по данному веществу равен
степени, в которой концентрация данного вещества входит в уравнение скорости
реакции. Сумма показателей степеней, в которых концентрация всех исходных
веществ входит уравнение скорости
реакции, равна порядку реакции в целом. Порядок химической реакции по веществу
совпадает со стехиометрическим коэффициентом реакции лишь в очень простых реакциях, например в
реакции синтеза йодистого водорода:
H2 + I2 ® 2HI.
Порядок этой реакции по водороду (первый) и
йоду (первый) равны стехиометрическими коэффициентами, а общий порядок реакции (второй) равен сумме
стехиометрических коэффициентов в уравнении скорости реакции
![]()
В подавляющем большинстве случаев порядок реакции по веществу
отличается от стехиометрических коэффициентов уравнения реакции для этого
вещества.
Соответственно общий порядок реакции обычно не
равен сумме стехиометрических коэффициентов уравнения реакции.
Например, для реакции
2N2O5 ® O2 + 2N2O4
порядок
реакции по N2O5 равен не двум, а единице.
Это обусловлено тем, что реакция
2N2O5 ® O2 + 2N2O4
протекает по стадиям:
1. N2O5 ® NO2 + NO3;
2. NO3 ® NO + NO2;
3. NO + NO3 ® 2NO2.
Причём самая медленная стадия – вторая.
Именно поэтому реакция разложения N2O5 имеет экспериментально
определённый первый порядок, т.е. скорость реакции
2N2O5 ® O2 + 2N2O4
в зависимости от концентрации N2O5 можно описать уравнением
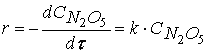
Уравнение, выражающее зависимость скорости
реакции от концентрации каждого вещества, называют кинетическим уравнением
реакции.
К сожалению, кинетическое уравнение реакции
может быть получено только при её экспериментальном изучении и не может быть
выведено из стехиометрического уравнения.
1.4. Реакция первого порядка
Реакция первого порядка
может быть записана в общем виде:
аA®продукты.
Примером такой реакции может служить реакция
разложения диметилового эфира:
CH3OCH3® CH4
+ H2 + CO.
Кинетическое уравнение реакции первого
порядка можно представить уравнением
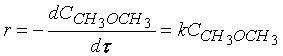 (1.5)
(1.5)
Разделив переменные и проинтегрировав,
получим
![]() , (1.6)
, (1.6)
где
С – концентрация CH3OCH3 в момент времени t.
Постоянная интегрирования может быть
определена из начальных условий:
при
t = 0 концентрация CH3OCH3 С = С0 и lnC = lnС0;
С0 – исходная концентрация.
И тогда зависимость
концентрации исходного вещества CH3OCH3
от
времени проведения процесса:
![]() . (1.7)
. (1.7)
Из (1.7) следует, что
концентрация исходного вещества со временем изменяется по экспоненциальному
закону:
![]() .
.
|
Проиллюстрируем изменение концентрации в
зависимости от времени на примере реакции первого порядка A ------> B с начальной
концентрацией
|
|
|
|
|
|
|
Рис.1. Зависимость концентрации
от времени в реакции первого
порядка.
и, в логарифмических
координатах, согласно зависимости
![]()
|
|
|
|
|
|
|
|
|
|
Рис.2. Зависимость
логарифма
концентрации исходного вещества
от времени в реакции первого порядка.
Поскольку
![]()
и скорость реакции по веществу А определяется как
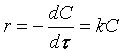 ,
,
то зависимость скорости реакции первого порядка
можно выразить соотношением
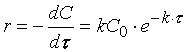 ,
,
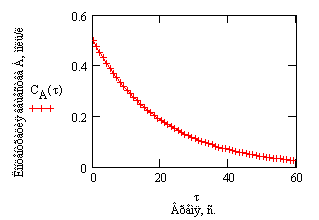
иллюстрацией которого служит рис.3.
|
|
|
|
|
|
Рис.3. Зависимость скорости
реакции первого порядка от времени
протекания
процесса.
Итак, если реакция протекает по первому порядку, то концентрация
реагирующего вещества во времени меняется по уравнению (1.7)
![]() (1.7)
(1.7)
В (1.7) иногда удобно натуральный логарифм
заменить десятичным:
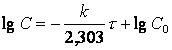 (1.8)
(1.8)
Графически в координатах (lnc, t) эта зависимость линейна с тангенсом угла
наклона, равным tgά= –![]() (рис.1.).
(рис.1.).
Немного преобразовав (1.7)
![]()
получим
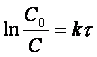
и
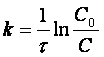 (1.9)
(1.9)
или
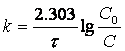 . (1.10)
. (1.10)
Рассчитаем период полупревращения (или полураспада) τ1/2,
т.е. время, необходимое для того, чтобы прореагировала половина исходного
количества вещества.
Подставляя C =(1/2)C0 в
(1.9), получим
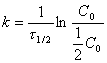 ,
,
откуда
![]() (1.12)
(1.12)
Особенностью реакции первого порядка является
независимость периода полупревращения от концентрации реагента.
Обратная величина константы скорости реакции первого
порядка имеет физический смысл средней продолжительности жизни отдельной
молекулы.
Попробуйте доказать это положение.
1.5. Реакции второго порядка
К таким реакциям принадлежат
реакции, скорость которых пропорциональна концентрации каждого из реагирующих
веществ или квадрату концентрации одного из них:
A + B → продукты,
![]() (1.13а)
(1.13а)
или,
если CA = CB, то
![]() (1.13б)
(1.13б)
Пусть
a и b – начальные концентрации C0 вещества A и B, а x –
число молей в 1 л, которое прореагировало за время ![]() .
.
Тогда
![]() (1.14)
(1.14)
Если начальные концентрации веществ А и В равны,
т.е. a = b, тогда (1.14) превращается в
![]() (1.15)
(1.15)
Уравнения (1.14) и (1.15) – кинетические
уравнения бимолекулярной реакции.
Найдем теперь кинетическое уравнение такой
реакции в интегральной форме, т.е. зависимость концентрации реагирующих веществ
от времени.
Разделим переменные:
![]()
Интегрирование этого уравнения даёт:
![]() (1.16)
(1.16)
Постоянная
интегрирования определяется из начальных условий:
x = 0 при τ = 0,
тогда const = 1/a и
![]() (1.17)
(1.17)
откуда
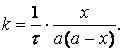 (1.18)
(1.18)
Уравнение (1.18) можно привести к другому
простому виду.
Подставляя C0 = a, a – x = C, x = C0 – C в (1.17), получим
![]() (1.19)
(1.19)
или
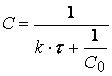
и
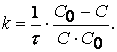 (1.20)
(1.20)
Напомним, что такой
результат мы получим только в случае равенства начальных концентраций веществ А
и В.
Проиллюстрируем изменение концентрации в зависимости
от времени на примере реакции второго порядка
2A ------> B
с начальной
концентрацией ![]() и константой скорости при некоторой температуре Т
и константой скорости при некоторой температуре Т ![]()
Согласно
(1.19) зависимость концентрации исходного вещества от времени проведения
процесса определяется соотношением:
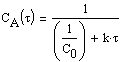
Нетрудно заметить, что в
координатах «обратная концентрация- – время» зависимость линейна.
Действительно, обозначим:
![]()
Тогда зависимость обратной концентрации от времени:
![]()
и зависимость
скорости реакции от времени
![]()
Иллюстрацией
полученных зависимостей служат рис. 4-6.
|
|
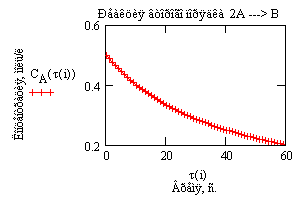
Рис. 4. Зависимость концентрации исходного
вещества от времени проведения процесса
|
|
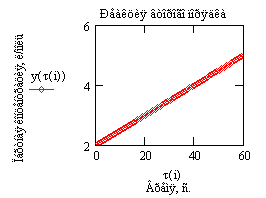
Рис.5. Зависимость обратной
концентрации исходного вещества
от времени проведения процесса
|
|
Рис.6. Зависимость скорости
реакции
второго порядка от
времени
проведения процесса.
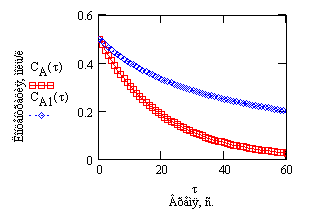
Сравним ход зависимостей концентрации
исходного вещества от времени проведения процесса для реакции первого и второго
порядка, разумеется, при одинаковых значениях начальных концентраций и
одинаковых числовых значениях констант скоростей.
|
|
|
|
|
|
Соотношения,
определяющие
зависимость
концентрации
исходного
вещества от времени
для
реакции первого
|
|
и
второго порядка
|
|
|
|
|
Рис.
Зависимость концентрации исходного вещества от
времени проведения процесса.
Начальные
концентрации исходных веществ Константы
скорости численно равны 0.05 |
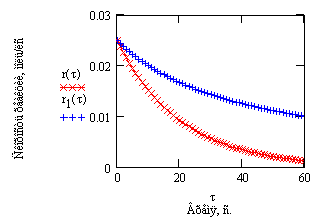
Такой ход зависимостей концентрации от
времени становится понятным после сравнения зависимостей скорости реакций от
времени проведения процесса.
|
|
Соотношения,
определяющие
|
|
|
|
зависимость
концентрации
исходного
вещества от времени
для
реакции первого
|
|
и
второго порядка
|
|
|
|
|
Рис.
Зависимость скорости реакции от времени
проведения процесса.
Начальные
концентрации исходных веществ Константы
скорости численно равны 0.05 |
Если
начальные концентрации реагирующих веществ не равны, необходимо интегрировать
уравнение (1.14)
![]() (1.14)
(1.14)
Интегрирование (1.14) по частям или методом
неопределённых коэффициентов приводит
к выражению:
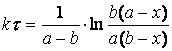 (1.21)
(1.21)
или
![]() (1.22),
(1.22),
где
![]() ,
, ![]() и x –
число молей в 1л, которое прореагировало за время τ.
и x –
число молей в 1л, которое прореагировало за время τ.
Заметим попутно, что наличие современных
компьютерных математических пакетов, например, таких, как MathCAD,
практически устраняет трудности, возникающие при решении подобных задач.
Проиллюстрируем это небольшим примером.
Как
уже упоминалось, в случае неравенства начальных концентраций при протекании
процесса
A + B → продукты
кинетическое
уравнение имеет вид (1.14)
|
|
и
время, за которое прореагирует x молей, может быть рассчитано
по соотношению
|
|
Тогда с помощью символьного процессора MathCAD
этот
интеграл легко вычисляется.
Для вычисления неопределенного интеграла от
некоторого выражения, например, рассматриваемого
|
|
по
определенной переменной (в нашем случае переменной является Х) выделяют в этом
выражении переменную и выполняют команду Symbolcs/Variable/Integrate.
После выполнения команды появляется
вычисленное аналитическое представление неопределенного интеграла:
|
|
Сравните это выражение с полученными ранее соотношениями
(1.21) или (1.22)
Рассмотрим еще один подход к решению задач по
определению зависимости концентрации реагирующих веществ от времени проведения
процесса.
Рассмотрим реакцию омыления эфира в щелочном
растворе
![]()
Исследуемая реакция является типичной
реакций
второго порядка, а, значит, ее скорость
описывается кинетическим уравнением (введя обозначения ![]() и
и ![]() )
)
![]()
При 298К константа скорости равна ![]()
Пусть начальные концентрации равны ![]() и
и ![]()
Рассчитаем изменение концентраций
реагирующих веществ в зависимости от времени протекания процесса.
Запишем кинетические
уравнения:
![]()
![]()
![]()
Решим
систему дифференциальных уравнений, т.е. найдем зависимость концентраций
исходных веществ и продуктов реакции в зависимости от времени.
Определим систему через формальную запись в
MathCAD.
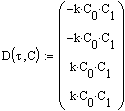
где ![]() ,
, ![]() .
.
Определим начальные условия
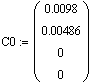
Введем значение константы скорости
исследуемой реакции
![]()
Результаты решения (с помощью имеющейся в
MathCAD встроенной функции, позволяющей решать систему методом Рунге-Кутты с фиксированным шагом)
представлены в матрице результатов и на рис. 7.
В левом столбце матрицы находятся значения аргумента
![]() ,делящие интервал на
равномерные шаги, в остальных столбцах - значения
,делящие интервал на
равномерные шаги, в остальных столбцах - значения ![]() ,
, ![]() ,
,![]() и
и ![]() .
.
|
|
В левом столбце матрицы находятся значения аргумента
![]() ,делящие интервал на
равномерные шаги, в остальных столбцах - значения
,делящие интервал на
равномерные шаги, в остальных столбцах - значения ![]() ,
, ![]() ,
,![]() и
и ![]() .
.
|
|
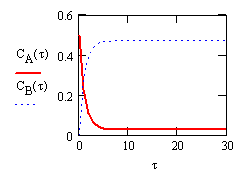
Рис.7. Зависимость концентрации
реагирующих
веществ от времени
(![]() -
концентрация эфира,
-
концентрация эфира,
![]() -
концентрация щелочи,
-
концентрация щелочи,
![]() -
концентрация спирта и
-
концентрация спирта и
![]() - концентрация ацетат иона)
- концентрация ацетат иона)
в
реакции омыления эфира
![]() при 298К.
при 298К.
Начальные
концентрации эфира ![]() и щелочи
и щелочи ![]()
Период полупревращения для реакции второго
порядка найдем из (1.20)
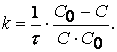
Подставив C = ½ C0, получим
![]()
Откуда время полупревращения для реакции
второго порядка в случае равенства начальных концентраций веществ А и В
![]() (1.23)
(1.23)
Для реакции второго порядка время полураспада
обратно пропорционально начальной концентрации исходного вещества.
1.6. Реакции других порядков
Реакции третьего порядка
встречаются достаточно редко, поэтому мы не будем их рассматривать. Отметим
только, что для реакции третьего порядка
A + B + C → продукты
кинетическое
уравнение имеет вид
![]()
Некоторые реакции, осложнённые
адсорбционными стадиями, имеют дробный порядок
![]() ,
,
где α <
1.
1.7. Методы определения порядка реакции
Мы уже упоминали, что обычно
химические реакции протекают через элементарные стадии, поэтому порядок реакции
может быть определён только экспериментально, и его нельзя вывести из
стехиометрического уравнения.
Обычно кинетический эксперимент заключается
в том, что исследователь получает данные о концентрациях реагирующих веществ во
времени в процессе реакции.
Эти данные
могут быть получены с помощью химического или физико–химического анализа.
Затем полученные данные о концентрации
реагирующих веществ во времени
подставляются в формулы для констант скорости реакции первого, второго и т.д.
порядка.
Критерием
справедливости кинетического уравнения может служить постоянство
величины k.
Рассмотрим такой подход на конкретном примере.
При исследовании разложения глюкозы в
водном растворе при температуре 350К были получены следующие результаты по
зависимости концентрации глюкозы от времени протекания процесса
t, мин. 0
45 120 240 480
960 1440 1920
2880 концентрация, моль/л 56.0
55.3 54.2 52.5
49.0 43.2 38.0
33.1 26.0
Определим порядок реакции и константу скорости при
этой температуре.
Рассматриваемая реакция принадлежит к
реакциям вида
A ------->
Продукты,
кинетическое уравнение которой в
дифференциальной форме имеет вид:
![]() ,
,
где n - порядок реакции и k - константа скорости.
Если порядок реакции
n =1, то интегрирование приводит
к выражению
![]()
Если порядок реакции отличен от единицы, т.е. ![]() , то интегрирование
, то интегрирование
![]()
для любого ![]() приводит к выражению
приводит к выражению
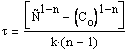
и.
например, для n = 2
![]()
Поскольку константа скорости не зависит от
концентрации, ее постоянство при различных значениях времени и соответствующему
этому времени концентрации вещества может служить критерием, по которому
определяется порядок реакции.
Так, например, для реакций первого порядка
![]() ,
,
для
реакций второго порядка
![]()
и для любого порядка, отличного от единицы
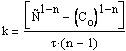
Предположим первый порядок реакции. Тогда при
подстановке в соотношение
![]()
значений времени и
соответствующих этому времени значений концентраций константа скорости реакции - в пределах
ошибки эксперимента - должна оставаться
постоянной.
Проверим это предположение:
рассчитаем константу скорости при
различных значениях времени и соответствующих этим значениям концентраций
глюкозы, подставив в
![]()
экспериментальные данные.
Результаты расчета
константы скорости по соотношению
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Полученные результаты свидетельствуют о
постоянном - в пределах ошибки эксперимента - значении константы скорости.
Среднее значение константы скорости
![]()
Это означает, что предположение о
первом порядке реакции справедливо.
Мы установили, что исследуемая реакция разложения
глюкозы является реакцией первого порядка и ее кинетическое уравнение в
дифференциальной форме - с учетом найденного значения константы скорости - можно выразить соотношением (где ![]() - обозначение расчетного значения концентрации
глюкозы, в отличии от С - ее экспериментального значения, приведенного в
условии задачи).
- обозначение расчетного значения концентрации
глюкозы, в отличии от С - ее экспериментального значения, приведенного в
условии задачи).
![]()
Кинетическое уравнение в интегральной форме
![]() ,
,
где ![]() - начальная концентрация исходного
вещества.
- начальная концентрация исходного
вещества.
Рассчитаем согласно
![]()
значения
концентрации глюкозы в зависимости от времени и сравним полученные результаты с
экспериментальными данными, приведенными в
условии задачи.
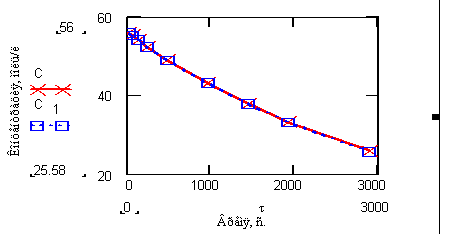
Рис.8. Зависимость
концентрации глюкозы от времени проведения
реакции ее разложения в водном растворе при температуре 350К ( С -
экспериментальные результаты, ![]() -
результаты расчета по кинетическому уравнению первого порядка.
-
результаты расчета по кинетическому уравнению первого порядка.
Порядок реакции может быть определён также
графически.
Так, например, если реакция подчиняется
кинетическому уравнению первого порядка,
то, в соответствии с (1.8):
![]()
график
зависимости в координатах (lnc, t) представляет собой прямую линию

Рис.9. Зависимость
концентрации исходного вещества от времени проведения для реакции первого
порядка.
Если же реакция подчиняется кинетическому уравнению
второго порядка, то линейная зависимость
должна наблюдаться в координатах (1/C, t), что следует из (1.19):
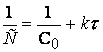
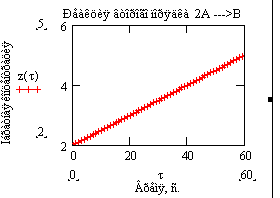
Рис.10. Зависимость
концентрации от времени проведения
реакции второго
порядка.
Порядок реакции и значение константы
скорости могут быть определены по данным о зависимости времени полупревращения
от начальной концентрации.
Время полупревращения ![]() связано с порядком реакции n и начальной
концентрацией
связано с порядком реакции n и начальной
концентрацией ![]() следующим соотношением:
следующим соотношением:
![]() =
= ![]()
Или, для газообразных веществ, поскольку
концентрация газа пропорциональна его
парциальному давлению:
![]() =
= ![]()
И после логарифмирования:
![]() =
= ![]()
Графически полученная зависимость
представляет собой прямую с тангенсом угла наклона, равным (1 - n), что
дает возможность определить порядок реакции.
Рассматриваемый
метод особенно полезен при дробном порядке реакции.
Рассмотрим несколько
подробнее этот метод на конкретном примере.
При исследовании реакции разложения аммиака на
вольфраме в качестве катализатора
2![]() ------->
-------> ![]() + 3
+ 3![]()
при
температуре 1173К были получены следующие данные о зависимости
времени полупревращения ![]() от начального давления аммиака
от начального давления аммиака ![]() (продукты реакции в начальный момент
отсутствуют):
(продукты реакции в начальный момент
отсутствуют):
![]() ,Па
,Па ![]() ,с.
,с.
3.33 0.9
5.33 1.62
10.66 3.36
18.63 7.5
33.0 10.8
Определим по этим данным порядок реакции по
аммиаку n и константу скорости реакции при
температуре 1173К.
Однако, построим,
прежде всего, график зависимости времени полупревращения ![]() от
начального давления:
от
начального давления:
|
|
|
Рис. 11. График зависимости времени
полупревращения в реакции разложения аммиака на вольфраме в качестве
катализатора 2 от начального давления при Т= 1173К |
С учетом неизбежного экспериментального
разброса данных, зависимость близка к линейной, что возможно только в том
случае, когда порядок реакции n = 0.
Результатом может быть вывод о том, что
кинетика реакции разложения аммиака на
вольфраме подчиняется уравнению нулевого
порядка.
- ![]() =
=![]()
С
учетом этого, уравнение, отражающее связь между временем полупревращения и
начальным давлением аммиака, примет вид:
![]() =
= ![]()
![]()
Полученное
соотношение дает возможность рассчитать
значение константы скорости реакции при
Т=1173К
k(1173) =1.453 Па/с
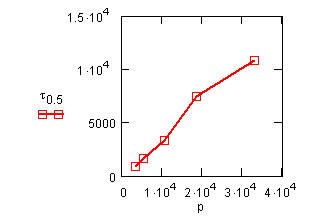
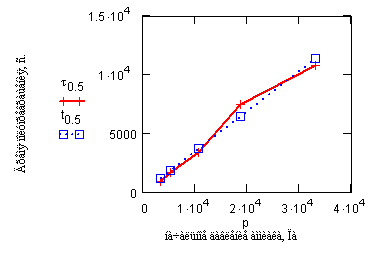
Сравнение экспериментальных данных по
периоду полупревращения в зависимости от начального давления аммиака при 1173К,
представленных в условии задачи, и расчетных данных по соотношению
![]() =
= ![]()
![]()
с учетом найденного
значения константы скорости реакции k(1173) =1.453 представлены на рис.12.
|
|
Рис.12. Экспериментальные (![]() ) и
расчетные (
) и
расчетные (![]() )
значения времени
)
значения времени
полупревращения в реакции разложения
аммиака на вольфраме
2![]() ------->
-------> ![]() + 3
+ 3![]()
в зависимости от начального давления
аммиака.
2. Сложные реакции
2.1 Большинство химических реакций
протекает не путем прямого превращения исходных веществ в продукты, а включает
несколько элементарных стадий.
При рассмотрении сложных реакций
используют основные принципы химической кинетики.
Принцип независимости: если в системе
протекает несколько реакций, то каждая из них подчиняется закону действующих
масс (основному закону химической кинетики) и протекает независимо от других
реакций.
Для элементарных стадий порядки по
реагентам равны стехиометрическим коэффициентам в уравнении этой стадии и общий
порядок совпадает с молекулярностью реакции. При этом для сложной реакции в
целом общий порядок реакции не совпадает с молекулярностью.
Часто скорость сложной реакции
определяется скоростью какой-либо одной стадии - лимитирующей.
Если реакция состоит из ряда последовательных
стадий, то лимитирующая стадия - наиболее медленная, а в случае параллельных
реакция - наиболее быстрая.
Часто химические реакции представляют
ряд последовательных и/или параллельных реакций различных порядков.
Для
таких реакций аналитическое (точное) решение найти трудно, а иногда и
невозможно.
Тогда при изучении кинетики прибегают к приближенному методу, который в
научной литературе получил название метода
стационарных, или квазистационарных концентраций. Метод предполагает, что скорость
образования промежуточного продукта приблизительно равна скорости его
разложения, т.е. скорость изменения
концентрации промежуточного продукта считается равной нулю.
Более подробно метод квазистационарных концентраций будет рассмотрен в
соответствующем разделе.
Рассмотрим применение указанных выше
принципов на примере реакции третьего порядка
![]() (2.1)
(2.1)
Экспериментально установлено, что эта
реакция имеет второй порядок по NO и
первый по О2. Кинетическое уравнение, связывающее скорость
образования продукта NO2 и концентрации исходных веществ NO
имеет вид:
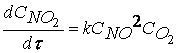 (2.2)
(2.2)
Реакция (2.1)
![]()
является сложной и протекает в виде двух элементарных стадий:
![]() быстрая (2.3)
быстрая (2.3)
![]() медленная (2.4),
медленная (2.4),
для
которых в соответствии с принципом независимости применим закон действующих
масс, причем показатели степеней концентраций NO, N2O2, O2 совпадают с молекулярностью реакций
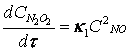 (2.5)
(2.5)
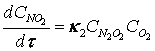 , (2.6)
, (2.6)![]()
то
есть обе реакции являются реакциями второго порядка.
Поскольку лимитирующей является
наиболее медленная стадия (2.4)
![]()
и ее скорость определяет скорость всего
процесса
![]() ,
,
то, казалось бы, кинетическое уравнение
лимитирующей стадии
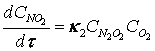 (2.6)
(2.6)
и должно описывать скорость всего
процесса.
Но эта реакция второго порядка, а
экспериментально установлено, что суммарная реакция (2.1) имеет третий порядок.
Нет ли здесь противоречия между теорией и
экспериментом?
Нет.
Дело
в том, что реакция (2.3)
![]()
является обратимой, и концентрацию димера N2O2, соответствующую равновесной, можно определить, если
известна константа равновесия:
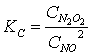 (2.7)
(2.7)
Медленное расходование димера N2O2 во второй стадии практически не изменяет его равновесной
концентрации, поэтому уравнение (2.6)
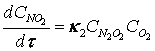 (2.6)
(2.6)
можно преобразовать, используя
соотношение (2.7)
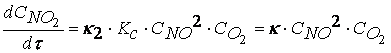 , (2.8)
, (2.8)
где ![]()
Уравнение (2.8) функционально полностью
совпадает с экспериментально найденным кинетическим уравнением (2.2)
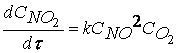 (2.2)
(2.2)
Более строгий подход к решению данной
задачи можно будет использовать после изучения кинетики сложных реакций (где
будет показано, что кинетическое уравнение (2.5) не совсем корректно).
Сложные реакции разделяются на три основных типа:
-
обратимые,
-
параллельные,
-
последовательные.
При рассмотрении сложных реакций часто
встречаются следующие задачи:
1. Составление кинетических уравнений для
элементарных стадий сложных реакций.
2. Вычисление концентраций (или степеней
превращения) компонентов в заданный момент времени ![]() по известному виду
кинетического уравнения и данным о константах скорости реакции.
по известному виду
кинетического уравнения и данным о константах скорости реакции.
3. Нахождение констант скоростей сложных реакций
из экспериментальных данных по концентрациям исходного вещества.
4. Расчет времени, необходимого для
достижения заданной концентрации реагентов.
2.1. Кинетика обратимых реакций
До сих пор мы рассматривали
необратимые реакции, т.е. реакции, скорость которых в прямом направлении много
больше скорости реакций в обратном направлении.
Однако имеются реакции, для которых скорости,
как в прямом, так и в обратном направлении соизмеримы.
Рассмотрим
реакции такого вида на простом примере обратимой реакций первого
порядка:
 (2.0)
(2.0)
В системе одновременно протекает прямая
реакция превращения вещества А в В с константой скорости ![]() и обратная реакция
превращения вещества В в А с константой скорости
и обратная реакция
превращения вещества В в А с константой скорости ![]() .
.
Если ![]() >>
>> ![]() или
или ![]() >>
>> ![]() , то реакция практически необратимо протекает в прямом или
обратном направлении.
, то реакция практически необратимо протекает в прямом или
обратном направлении.
Если же скорости прямой и обратной реакций
соизмеримы, то скорость такой реакции равна разности скоростей в прямом и
обратном направлениях:
![]() (2.1)
(2.1)
Уравнение (2.1) основано на принципе независимости протекания
различных реакций.
В основе
этого принципа лежит положение, что скорость каждой из нескольких одновременно
протекающих реакций не зависит друг от друга.
Справедливость этого принципа была
неоднократно проверена экспериментально.
Пусть обратимая реакция

имеет первый порядок в обоих
направлениях.
Обозначим через СОА и СОВ начальные концентрации исходного вещества и
продукта соответственно.
Тогда по принципу независимости скоростей
элементарных стадий скорости прямой и обратной реакции соответственно равны:
![]() (2.1)
(2.1)
![]() (2.2),
(2.2),
а
суммарная наблюдаемая скорость реакции равна сумме независимых скоростей прямой
и обратной реакции:
![]() (2.3)
(2.3)
![]() (2.4)
(2.4)
Мы уже отмечали, что при рассмотрении
сложных реакций часто встречаются следующие задачи:
-составление кинетических уравнений для
элементарных стадий сложных реакций и
-вычисление концентраций (или степеней
превращения) компонентов в заданный момент времени ![]() по известному виду
кинетического уравнения и данным о константах скорости реакции.
по известному виду
кинетического уравнения и данным о константах скорости реакции.
Рассмотрим решение этих задач на конкретном примере.
Пример
2.1.
Для реакции

найдите зависимость концентрации
прореагировавшего вещества А и образовавшегося В от времени, если их начальные
концентрации составили СОА и СОВ соответственно и известны константы скорости
![]() и
и ![]()
Решение:
Обозначим через ![]() уменьшение
концентрации исходного вещества (или увеличение концентрации продукта) к
моменту времени
уменьшение
концентрации исходного вещества (или увеличение концентрации продукта) к
моменту времени ![]() .
.
Тогда
после подстановки в уравнение (2.3)
![]()
и
(2.4)
![]()
значений
концентраций веществ A и B
CА=СОА -![]()
CВ=СОВ +![]()
получим:
![]() (2.5)
(2.5)
Преобразуем
дифференциальное уравнение (2.5), приведя его к виду:
![]() (2.6)
(2.6)
Разделим переменные:
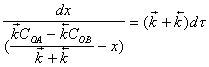 (2.7)
(2.7)
После
интегрирования получим:
![]() (2.8)
(2.8)
где
В - постоянная интегрирования, которую можно найти, используя начальные условия:
при ![]() =0
=0 ![]() =0.
=0.
Из
уравнения (2.8) найдем постоянную интегрирования:
![]() (2.9)
(2.9)
Подставив (2.9) в (2.8) и несколько преобразовав
полученное выражение, получим интегральную форму кинетического уравнения,
представляющую собой функцию ![]() при известных значениях
при известных значениях ![]() ,
,![]() ,
,![]() ,
,![]() :
:
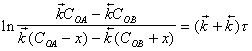 (2.10)
(2.10)
Пример 2.2.
Для условия предыдущей задачи найдите зависимость
концентраций веществ (A и B) ![]() и
и ![]() от времени, если
от времени, если ![]()
Решение:
Из уравнения (2.10)
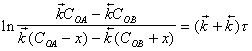
следует, что с учетом введенных обозначений ![]() и
и ![]() , текущие концентрации
веществ А и В:
, текущие концентрации
веществ А и В:
![]() (2.11)
(2.11)
![]() (2.11а)
(2.11а)
Основное отличие обратимых реакций от необратимых состоит в том, что обратимые реакции доходят в пределе не до конца, (когда при ![]()
![]() ), а до состояния равновесия, при котором
), а до состояния равновесия, при котором ![]() , и общая скорость реакции становится равной нулю:
, и общая скорость реакции становится равной нулю:
![]() (2.12)
(2.12)
где ![]() - изменение
концентрации при равновесии.
- изменение
концентрации при равновесии.
Пример 2.3.
Покажите, что отношение констант скоростей
прямой и обратной реакции

равно константе равновесия ![]() .
.
Решение.
Из уравнения (2.12), характеризующего общую
скорость реакции при равновесии
![]()
следует, что
![]() (2.13)
(2.13)
где
![]() ,
, ![]() - равновесные
концентрации веществ B и A.
- равновесные
концентрации веществ B и A.
Пример 2.4.
Для реакции, имеющей первый порядок в прямом
направлении и второй в обратном
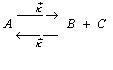 (2.14)
(2.14)
найдите
дифференциальные и интегральные кинетические уравнения ![]() , если начальные концентрации продуктов реакции
, если начальные концентрации продуктов реакции ![]()
Решение.
Для
момента ![]() кинетическое уравнение
имеет вид
кинетическое уравнение
имеет вид
![]() (2.15)
(2.15)
![]() Разделим переменные в дифференциальном
уравнении (2.15):
Разделим переменные в дифференциальном
уравнении (2.15):
Преобразуем
трехчлен следующим образом
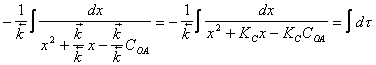
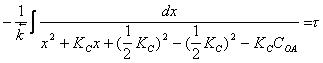
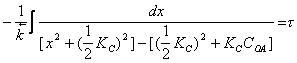
Введем
обозначения
![]() и
и ![]()
Тогда интеграл
сводится к табличному интегралу:
![]()
или
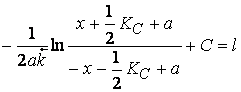 (2.16)
(2.16)
Постоянная
С находится из начальных условий:
при
![]()
![]()
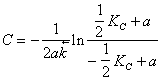
Не
очень простые преобразования, не правда ли?
Однако наличие современных компьютерных
математических пакетов, например, таких, как MathCAD, практически устраняет
трудности, возникающие при решении подобных задач.
Покажем это на примере 2.4.
(Напомним
эту задачу).
Для реакции, имеющей первый порядок в прямом
направлении и второй в обратном
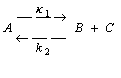 (2.17)
(2.17)
запишите дифференциальные и интегральные кинетические
уравнения ![]() , если при τ=0
, если при τ=0 ![]() и
и ![]() .
.
Решение.
Определим текущие концентрации продуктов
реакции:
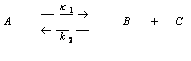
Исходная
концентрация,
моль/л ![]() 0 0
0 0
Прореагировало
к
моменту
τ,
моль/л ![]()
![]()
![]()
Концентрация
в
момент
τ,
моль/л ![]()
![]()
![]()
Тогда
кинетическое уравнение исследуемой реакции
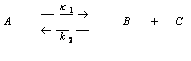
можно
представить:
|
|
Задача сводится к решению этого
дифференциального уравнения, т.е. к нахождению зависимости концентрации
вещества А от времени ![]() .
.
Для численного интегрирования одного
обыкновенного дифференциального уравнения первого порядка у пользователя
математического пакета MathCAD
имеется вычислительный блок Given/Odesolve.
Зададим
значение начальной концентрации вещества А и значения констант скоростей
прямого и обратного процессов при некоторой температуре реакции.
![]()
![]()
![]()
Введем
ключевое слово
Given
Введем соотношение, определяющее
дифференциальное уравнение
|
|
Введем начальные условия – значение
концентрации исходного вещества при τ=0
|
|
Введем встроенную функцию для решения
дифференциального уравнения относительно переменной ![]() на интервале (τ0,
τ1).
на интервале (τ0,
τ1).
|
|
Мы можем определить зависимость от времени
концентрации не только исходного вещества, но и продукта реакции. Для этого введем
соотношение, определяющее зависимость концентрации продукта реакции от времени:
|
|
Вывод решения дифференциального уравнения
- зависимость концентрации исходного вещества и продукта реакции

от
времени
|
|
|
|
|
|
Результаты
иллюстрирует рис.9.
|
|
Таким образом, в реакции

через 8 минут (или секунд, в зависимости от
размерности констант скоростей) наступает состояние равновесия.
Мы уже отмечали, что при рассмотрении
сложных реакций часто встречаются следующие задачи:
-нахождение констант скоростей сложных
реакций из экспериментальных данных по концентрациям исходного вещества.
-расчет времени, необходимого для
достижения заданной концентрации реагентов.
Рассмотрим подходы к решению подобных задач
на конкретном примере.
Пример 2.5
При 298К была изучена реакция изомеризации b - оксикро-
тонового эфира в ацетоуксусный
эфир.
Ниже
представлены данные о концентрации
исходного вещества (моль/л) в зависимости от времени (час) проведения процесса.
|
|
|
|
Определите по этим данным константы
скорости прямой и
обратной реакции.
Решение.
Исследуемая реакция относится к обратимым
реакциям вида
A <====> B
с константой скорости ![]() в прямом и константой скорости
в прямом и константой скорости ![]() в обратном направлении.
в обратном направлении.
Тогда кинетическое уравнение реакции
![]() ,
,
где ![]() - текущая концентрация исходного вещества,
- текущая концентрация исходного вещества,
![]() - начальная концентрация вещества А и
- начальная концентрация вещества А и ![]() начальная концентрация продукта реакции.
начальная концентрация продукта реакции.
Интегральная форма кинетического уравнения,
связывающего текущую концентрацию исходного вещества и время достижения этой
концентрации
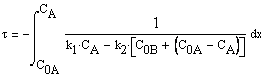
Подобные
соотношения можно записать для всех концентраций и соответствующих значений
времени достижения этих концентраций.
Поскольку константы скорости и константа
равновесия ![]() связаны соотношением
связаны соотношением
![]() ,
,
а константа равновесия
определяется как
![]() ,
,
где ![]() - концентрация исходного вещества и
- концентрация исходного вещества и ![]() - концентрация продукта реакции при
равновесии.
- концентрация продукта реакции при
равновесии.
Тогда
![]()
Таким образом, получена
система из двенадцати уравнений
 (i=1,11)
(i=1,11)
![]()
с двумя неизвестными ![]() и
и ![]() .
.
Решение системы с помощью встроенной функции
Minerr, имеющейся в математическом пакете MathCAD:
Minerr = 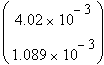
Тогда кинетическое уравнение исследуемой
реакции при 298К
![]()
и время достижения заданной концентрации
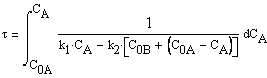
где ![]() и
и ![]()
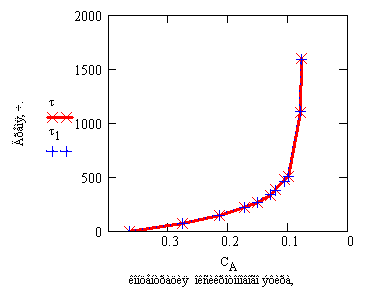
Ниже приведены экспериментальные (![]() ) данные по времени
достижения определенной концентрации исходного вещества, представленные в
условии задачи, и результаты
) данные по времени
достижения определенной концентрации исходного вещества, представленные в
условии задачи, и результаты ![]() , полученные с учетом
найденных значений констант скоростей прямой
, полученные с учетом
найденных значений констант скоростей прямой ![]() и обратной
и обратной ![]() реакций по уравнению
реакций по уравнению
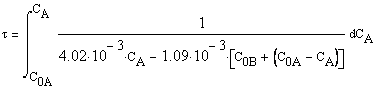
а
также их графическая иллюстрация.
|
|
|
|
|
|
|
|
|
Рис. 10. Время достижения заданной концентрации (моль/л)
|
2.2 Параллельные реакции
Довольно часто встречаются реакции, для которых термодинамика допускает превращения исходных веществ сразу в нескольких направлениях, например,
![]() N2+2H2
N2+2H2
![]() 4N2H4
4N2H4
N2+4NH3
или
в общем виде
![]() B
B
k1
![]() А
А
k2
C
Такие реакции называют параллельными.
Параллельными называются реакции, в
которых исходные вещества вступают одновременно в две или более реакции.
Рассмотрим кинетику параллельных реакций на
простейшем примере, когда исходное вещество А одновременно превращается по
реакции первого порядка в вещество В и С:
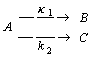 (2.18)
(2.18)
Пример 3.1.
Найдите для реакции
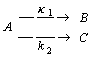
аналитическую зависимость концентрации
вещества А от времени ![]() , если продукты реакции в начальный момент отсутствуют
, если продукты реакции в начальный момент отсутствуют ![]()
Решение.
Запишем кинетическое уравнение реакции,
используем принцип независимости для реакции
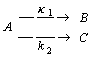
согласно которому общее изменение концентрации равно
сумме независимых изменений:
![]() (2.19)
(2.19)
Дифференциальное уравнение (2.19) легко
интегрируется, в результате чего получаются уравнения, схожие с уравнением
первого порядка:
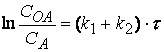 (2.20)
(2.20)
или
![]() (2.21)
(2.21)
Пример 3.2.
Найдите аналитическую зависимость концентрации
продуктов реакции
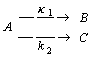
от времени проведения процесса ![]() ,
,![]() , если их начальные концентрации
, если их начальные концентрации ![]() ,
, ![]()
Решение.
Запишем кинетические уравнения исследуемой
реакции
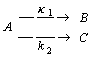
по продуктам.
По принципу независимых скоростей
![]() (2.23)
(2.23)
![]() (2.24)
(2.24)
Но из уравнения (2.21) следует, что
![]()
Тогда
![]()
![]() (2.25)
(2.25)
После интегрирования (2.25) с учетом, что ![]() и
и ![]() , получим
, получим
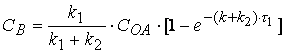 (2.26)
(2.26)
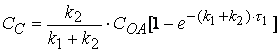 (2.27)
(2.27)
Пример 3.3. Найдите соотношение концентрации ![]() и
и ![]() для реакции
для реакции
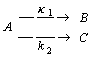
в любой момент времени.
Решение.
Разделив
(2.26) на (2.27), получим соотношение
![]() (2.28)
(2.28)
показывающее,
что в процессе реакции
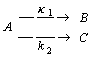
отношение концентраций продуктов остается
постоянным и равным отношению констант скоростей.
Рассмотрим
еще один – более сложный - пример.
Пример 3.4
Исследовалась при 1300К параллельная
реакция
![]() N2+O2 (константа скорости
N2+O2 (константа скорости ![]() )
)
![]() 2NO
2NO
N2O+0.5O2 (константа скорости ![]() )
)
При 1300К были получены следующие значения
констант скоростей реакций: ![]() и
и ![]()
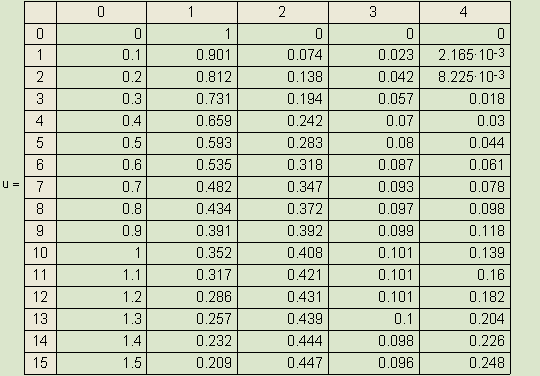
Определите зависимость
концентраций исходных веществ и продуктов реакции при 1300К, если исходная
концентрация оксида азота С=4 моль/л.
Решение.
Запишем кинетические уравнения по каждому
реагенту:
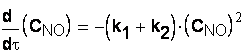
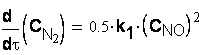

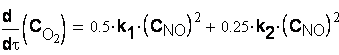
Остается решить систему дифференциальных
уравнений для определения концентраций исходного вещества и продуктов реакции в
зависимости от времени проведения процесса.
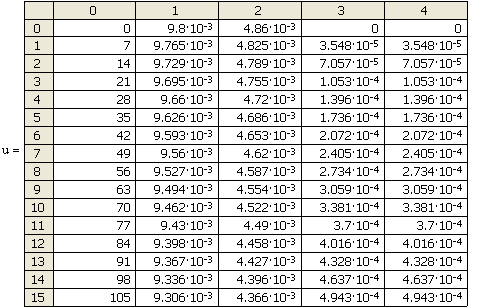
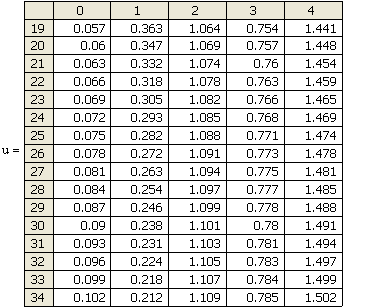
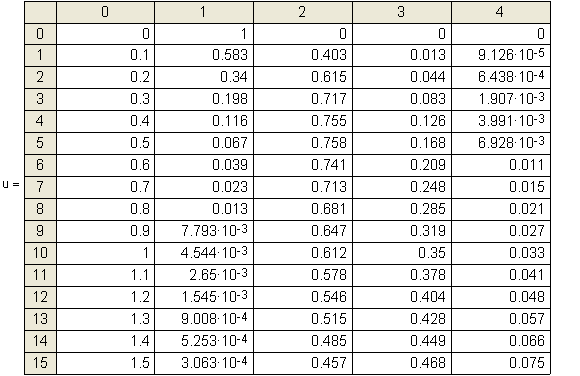
Ниже в
матрице результатов u
приведено решение системы с помощью имеющейся в
распоряжении пользователя математического пакета MathCAD встроенной функции ![]() , которая позволяет решать
поставленную задачу методом Рунге-Кутты с фиксированным шагом.
, которая позволяет решать
поставленную задачу методом Рунге-Кутты с фиксированным шагом.
Матрица результатов u
|
|
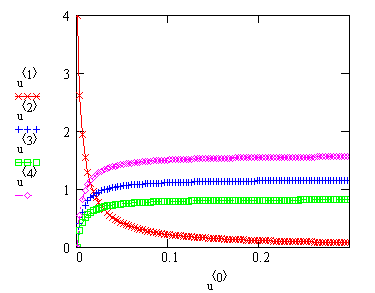
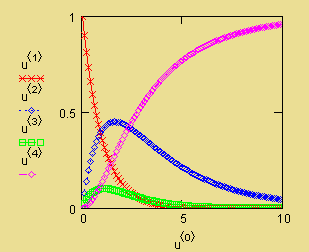
В матрице u
приняты обозначения:
![]() - время, с.;
- время, с.;
![]() - концентрация NO;
- концентрация NO;
![]() - концентрация
- концентрация ![]() ;
;
![]() - концентрация
- концентрация ![]() ;
;
![]() - концентрация
- концентрация ![]()
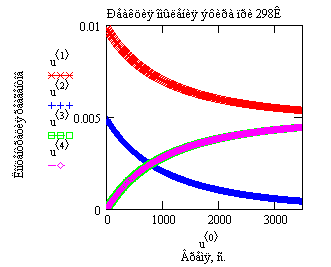
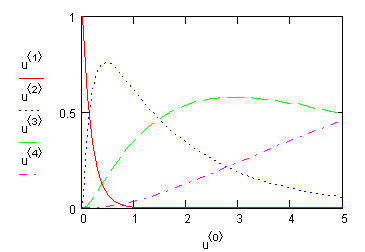
Графическая иллюстрация полученных
результатов представлена на рис.11.
|
|
|
Рис.11.
Зависимость концентрации реагирующих веществ от времени проведения процесса
N2O+0.5O2 при 1300К. |
Последовательные реакции
Часто
встречаются реакции вида
![]()
При протекании последовательных реакций
образование конечного продукта из исходных веществ происходит не
непосредственно, а через один или несколько промежуточных продуктов, которые
часто являются неустойчивыми
![]()
Из схемы реакции видно, что вещество А
сначала превращается в вещество В и только потом в вещество С, т.е. реакция
протекает через промежуточные стадии. Вообще
говоря, большинство реакций протекают через промежуточные стадии, однако не
всегда экспериментально удаётся их выявить.
В качестве примера последовательных реакций
можно привести реакцию термического крекинга углеводородов.
Мы рассмотрим самый простой случай:
![]() (2.28)
(2.28)
т.е.
случай двух последовательных необратимых мономолекулярных реакций.
Наша задача: установить зависимости, по
которым меняются со временем
концентрации веществ А, В, С, и исследовать характер этих зависимостей.
Напишем кинетические уравнения для каждой из
реакций.
Для реакции
![]()
это
будет, очевидно, уравнение для мономолекулярной
реакции первого порядка
![]() (2.29)
(2.29)
Концентрация вещества B будет
возрастать за счёт реакции
![]() ,
,
поэтому для реакции
![]()
![]() (2.30)
(2.30)
И, наконец, концентрация вещества С будет
меняться со временем:
![]() (2.31)
(2.31)
Итак, мы имеем систему дифференциальных
уравнений (2.29 – 2.31), которую необходимо решить, чтобы найти зависимости, по
которым будут меняться концентрации веществ A, B и С со временем.
Будем считать, что при τ =
0 CA = CA0, CВ = 0 и CС = 0.
Из (2.29) следует, что
![]() (2.32)
(2.32)
эта
зависимость уже встречалась нам при интегрировании кинетического уравнения
реакции первого порядка.
Подставив полученное выражение в (2.30)
![]() ,
,
получим
![]() (2.33)
(2.33)
Решение этого дифференциального уравнения
имеет вид
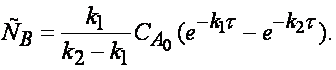 (2.34)
(2.34)
Интересной особенностью
кинетики последовательных реакций является то, что концентрация промежуточного
вещества как функция времени проходит через максимум, в чём легко убедиться,
исследовав (2.34) на экстремум:
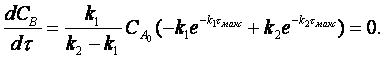
Тогда
![]()
и
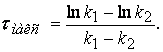 (2.35)
(2.35)
Максимальную концентрацию
вещества В можно найти, подставив значение τмакс в (2.34).
Концентрацию вещества С можно определить,
если учесть, что сумма концентраций всех веществ в любой момент времени реакции
остаётся постоянной, т.е.
![]() .
.
Тогда
![]()
Используя соотношения (2.32) и (2.34) для CA и CB, получим
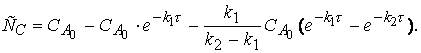
Практическое приложение полученных
закономерностей можно проиллюстрировать следующим примером.
В
некоторых случаях нас может интересовать выход промежуточного продукта B, а
вещество C, наоборот, только загрязняет его. Основываясь на
экспериментальных данных о значениях констант скоростей стадий, мы можем по (2.35)
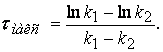
предсказать оптимальное время выхода продукта.
Пример 3.5.
Для двух последовательных односторонних
реакций первого порядка
![]() (2.36)
(2.36)
выведите
аналитическую зависимость концентрации промежуточного вещества P от времени, если ![]() .
.
Решение:
В соответствии с принципом независимости,
кинетические уравнения в дифференциальной форме для двух стадий запишем в виде:
![]() (2.37)
(2.37)
![]() (2.38)
(2.38)
Промежуточное вещество P образуется в первой стадии и
расходуется во второй
![]() (2.39)
(2.39)
Подставив
в (2.39) интегральное кинетическое уравнение для вещества А (2.32)
![]() (2.32),
(2.32),
получим для полупродукта P следующее дифференциальное уравнение:
![]() (2.40)
(2.40)
Решение этого дифференциального
уравнения первого порядка осуществляется умножением обеих частей уравнения на
интегрирующий множитель ![]() . Получаем в левой части уравнения (2.40) полную производную
функции
. Получаем в левой части уравнения (2.40) полную производную
функции ![]() . При интегрировании в этом случае от 0 до
. При интегрировании в этом случае от 0 до ![]() и от 0 до
и от 0 до ![]() :
:
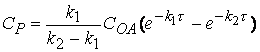 (2.41)
(2.41)
Интересно отметить, что функция (2.41)
имеет максимум, в чем легко убедиться, подставляя значение ![]() и
и ![]() в уравнение (2.41).
в уравнение (2.41).
Пример 3.6.
Выведите выражения, определяющие максимальную
концентрацию промежуточного вещества P
и время достижения его максимальной концентрации.
Решение: Приравнивая производную функции (2.42)
по времени к нулю и затем, логарифмируя это выражение, получим
 (2.44)
(2.44)
Найдем
максимальную концентрацию P,
подставляя (2.44) в (2.41)
 (2.42)
(2.42)
откуда
следует, что максимальная концентрация вещества P зависит от начальной концентрации
реагента А и соотношение констант ![]() .
.
Пример
3.6.
Для реакции
![]()
выведите
зависимость концентрации вещества В от времени, если ![]() .
.
Решение.
Применим условие материального баланса
для исследуемой реакции: в любой момент
времени начальная концентрация вещества А связана с текущими концентрациями
веществ Р и В следующим соотношением:
![]() (2.43)
(2.43)
Подставляя
![]()
и
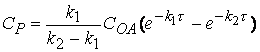
в (2.43)
![]()
получим:
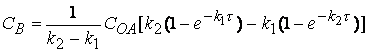 (2.44)
(2.44)
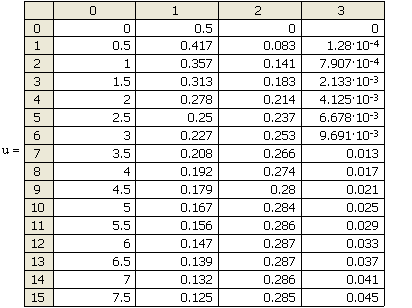
Пример изменения концентрации реагентов
от времени в реакции
![]()
в соответствии с полученными уравнениями
приведен на рис.12.
|
|
|
Рис.12 Зависимость
концентрации исходного вещества A ---> B ---> C при значении констант
скоростей: Начальная концентрация вещества
A равна 0.5 моль/л. |
Возможности, реализуемые при применении
компьютерного математического пакета MathCAD при
решении подобных задач, демонстрирует пример 3.7.
В распоряжении пользователя пакета MathCAD имеется встроенная функция rkfixed(y0,t1,M.D), позволяющая решать системы
обыкновенных дифференциальных уравнений методом Рунге – Кутты с фиксированным
шагом.
Здесь
- y0, вектор
начальных значений в точке t0 размера Nx1, t0 – начальная точка расчета, t1 – конечная точка расчета, M –
число шагов, на котором численный метод находит решение, D – векторная функция размера Nx1 двух аргументов – t и
y.
При
этом y – искомая
векторная функция аргумента t того же размера Nx1.
Функция rkfixed выдает решение в виде матрицы.
Пример
3.7.
По известным значениям констант
скоростей отдельных стадий превращения циклической трифосфорной кислоты в
монофосфорную рассчитайте текущие концентрации всех участников реакции -
циклической трифосфорной кислоты (A),
трифосфорной цепочечной (B), дифосфорной (C) и монофосфорной (D) при 333К.
A
---->B ------->C ----->D
![]()
![]()
![]()
![]() 1/ч;
1/ч; ![]() 1/ч;
1/ч; ![]() 1/ч
1/ч
Решение.
Кинетические уравнения:
по веществу A
![]()
по веществу B
![]()
по веществу C
![]()
и по веществу D
![]()
Введём
векторную функцию, определяющую систему дифференциальных уравнений.
|
|
Ввод
начальных условий: начальная концентрация вещества А СА=1моль/л,
СB
= СC=СD=0.
|
|
Ввод
числа шагов, на которых рассчитывается решение:
|
|
|
|
Последняя строка листинга – присваивание
матричной переменной u
результата действия функции rkfixed
– решение системы будет осуществлено на промежутке 0, 10.
|
|
Вывод решения системы дифференциальных
уравнений – в нулевом столбце показано время от начала процесса, в первом столбце – значение концентрации
вещества А СА, во
втором – концентрации СB,
в третьем и четвертом – концентрации СC
и
СD,соответствующих
этому времени.
|
|
Графическая
иллюстрация полученных результатов представлена на рис.3.13.
Рис.3.13.
Зависимость концентрации СА, СB, СC и
СD
от
времени проведения последовательной реакции
![]()
Пример 3.7.
Для двух последовательных реакций второго
порядка:
![]()
![]() (2.45)
(2.45)
составьте
систему кинетических уравнений (систему дифференциальных уравнений) для расчета
зависимостей ![]()
Решение.
Запишем систему кинетических уравнений в
дифференциальной форме:
|
|
|
|
|
|
Получена система дифференциальных
уравнений, которую, разумеется, придется решать, чтобы получить зависимости
текущих концентраций реагентов.
Воспользуемся возможностями компьютерного математического пакета MathCAD при
решении подобных задач.
Введем
векторную функцию, определяющую систему дифференциальных уравнений.
|
|
Введем
начальные условия: начальная концентрация вещества А СА=0.5моль/л,
СB
= СP=0.
|
|
Введем
число шагов, на которых будет рассчитываться решение.
|
|
В последней строке листинга матричной переменной u присваивается результат действия
функции rkfixed
– решение системы будет осуществлено на промежутке 0, 50.
|
|
Вывод решения
системы дифференциальных уравнений:
|
|
в нулевом столбце показано время от
начала процесса,
в первом столбце – значение концентрации
вещества А СА,
во втором– концентрации СР
и в третьем – концентрации СВ, соответствующих
этому времени.
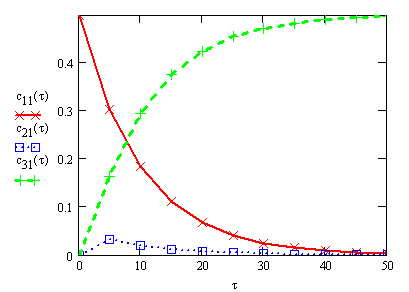
Графическая иллюстрация полученных
результатов приведена на рис.14.
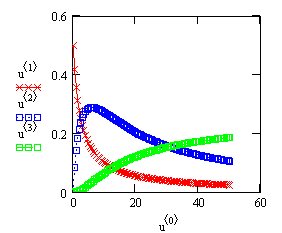
Рис.14.Зависимость концентрации СА,
СР и СВ т времени проведения последовательной
реакции ![]()
Пример 3.8.
Для
двух реакций первого порядка
![]()

Составьте
систему дифференциальных уравнений для расчета зависимостей ![]()
Решение:
Кинетические уравнения в дифференциальной
форме имеют вид
![]()
![]()
Подставим
в последнее уравнение условие материального баланса
![]()
Тогда получим:
![]() ,
,
и
искомая система дифференциальных уравнений для расчета зависимостей текущих
концентраций реагентов:
![]()
![]()
Пример 3.10
Фотохимическое хлорирование
в избытке хлора (его концентрацию можно считать постоянной) 3,4,5 - трихлор - 2(трихлорметил) пиридина (в
дальнейшем вещество А) можно рассматривать
как реакцию первого порядка, протекающую
по последовательно - параллельной схеме
![]()
![]()
A
--------> B ------------> D
A --------->C ------------> D
![]()
![]()
При 433К (по данным Емельянова В.И., Стуля Б.Я.,
Королева Б.М., Кинетика и катализ, 1984.-т.25, №3) константы скорости
соответственно равны ![]() =0.792,
=0.792,
![]() = 0.252,
= 0.252, ![]() = 0.324 и
= 0.324 и
![]() = 0.792 1/ч.
= 0.792 1/ч.
Рассчитайте концентрации
промежуточных и конечных продуктов в зависимости от времени протекания процесса
и постройте кинетические кривые.
Решение.
Кинетические уравнения в
дифференциальной форме для участников реакции имеют вид:
![]() (3.10.1)
(3.10.1)
![]() (3.10.2.)
(3.10.2.)
![]() (3.10.3.)
(3.10.3.)
![]() (3.10.4.)
(3.10.4.)
Решение.
Решим систему обычных дифференциальных
уравнений (3.10.1.) - (3.10.4.) методом Рунге - Кутты с фиксированным шагом.
Решение будем искать с помощью имеющейся в
математическом пакете MathCAD встроенной
функции rkfixed(y0, t0, t1, M, D).
Здесь y0 - вектор начальных значений в
точке t0, t0 - начальная точка расчета,
t1 - конечная точка расчета, M – число шагов, на которых численный метод
находит решение, D - векторная функция размера Nx1 двух аргументов - скалярного и векторного. При этом y - искомая векторная функция аргумента t того
же размера.
Для удобства введем обозначения: ![]() - текущая концентрация вещества A,
- текущая концентрация вещества A, ![]() - концентрация вещества B,
- концентрация вещества B, ![]() - концентрация вещества C и
- концентрация вещества C и ![]() - концентрация вещества D.
- концентрация вещества D.
Тогда:
|
|
|
|
|
|
|
|
|
|
|
В первой строке
листинга определена система
ОДУ. |
|
|
|
Во второй строке
листинга определен вектор начальных условий. |
|
В третьей строке
листинга определено число
шагов, на которых
рассчитывается решение. |
|
|
|
Последняя строка
присваивает матричной переменной
u результат действия функции
rkfixed. Решение системы будет
осуществлено на промежутке (0,10) |
|
|
|
|
Вывод решения
системы дифференциальных уравнений:
|
Обратите внимание на разно- чтение в обозначении индексов вектора начальных условий и матрицы
решения. В первом столбце матрицы собраны зна - чения нулевой компоненты ис -
комого вектора |
Графическая иллюстрация полученных
результатов приведена на рис.15.
|
|
|
Максимальное значение кон- центрации вещества В
|
|
Рис. 15. Кинетические кривые исходного вещества (1),
промежуточных соединений (2,3) и продукта (4) при протекании последовательно
- параллельной реакции A --------> B
------------> D A
--------->C ------------> D
|
Метод квазистационарных концентраций.
Следует отметить, что рассмотренные
выше системы дифференциальных уравнений, например:
![]()
![]()
допускают аналитическое решение, хотя и
достаточно сложное.
Можно себе представить, в какой степени
возрастает громоздкость уравнений в более сложных случаях, например при
нескольких последовательных и параллельных реакциях различных порядков.
Но расчеты существенно упрощаются, если
процесс может протекать в стационарных или квазистационарных условиях, что
часто реализуется на практике.
Используя метод стационарных концентраций,
можно существенно упростить систему дифференциальных уравнений, а иногда
удается свести ее к системе алгебраических уравнений.
Для пояснения сути этого метода вернемся к соотношениям,
определяющим максимальную концентрацию промежуточного соединения Р и время
достижения максимальной концентрации в последовательной реакции вида
A --->P---->B
 (4.8)
(4.8)
 (4.9)
(4.9)
На рис.16
показана зависимость концентрации промежуточного продукта Р от времени
проведения процесса для реакций первого порядка
A --->P---->B
при одинаковом отношении между константами ![]()
![]() .
.
Высота максимума ![]() для всех случаев будет
одинакова, но вид кривых различен, так как время достижения максимума согласно
(4.8)
для всех случаев будет
одинакова, но вид кривых различен, так как время достижения максимума согласно
(4.8)

зависит от констант реакции.
|
|
Рис.16. Зависимость концентрации
промежуточного соединения в последовательной реакции
A ---> B ---> C
при следующих значениях констант скоростей:
1. ![]() -
- ![]() = 0.1;
= 0.1;
![]() =
1). 2.
=
1). 2.![]() - (
- (![]() = 0.01;
= 0.01;
![]() =
0.1). 3.
=
0.1). 3. ![]() - (
- (![]() =0.001;
=0.001; ![]() =
0.01).
=
0.01).
Начальная
концентрация вещества A равна 1 моль/л.
Особый интерес представляет кривая 3,
показывающая, что уменьшение разности ![]() при том же их
отношении приводит к растягиванию максимума во времени.
при том же их
отношении приводит к растягиванию максимума во времени.
Концентрация промежуточного продукта
длительное время держится приблизительно на одном уровне, близком к
максимальному.
Это дает возможность считать, что по истечении
некоторого малого времени после начала реакции устанавливается приблизительно
стационарная (квазистационарная) концентрация неустойчивого промежуточного
продукта, сохраняющаяся в течение значительной части времени протекания
реакции.
Можно
считать, что в стационарном состоянии скорость образования промежуточного
продукта приблизительно равна скорости его разложения.
Поэтому суммарная скорость изменения концентрации промежуточного продукта равна
нулю, вернее считается равной нулю, не только в точке максимума, но
относительно длительное время.
В этом заключается приближенность метода
стационарных концентраций.
Рассмотрим несколько подробнее возможности
метода.
Пример 3.9. Используя метод стационарных
концентраций, найдите зависимость концентрации промежуточного вещества от
времени протекания процесса ![]() для реакции
для реакции
![]() ,
,
если
![]()
Решение.
Промежуточное вещество P образуется в первой стадии и
расходуется во второй
![]()
Согласно методу стационарных концентраций,
следует, что
![]() (4.16)
(4.16)
откуда
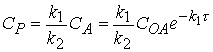 (4.17)
(4.17)
Пример 3.10.
Сравните точное решение для концентрации
промежуточного вещества
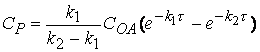
с приближенным решением согласно методу
квазистационарных концентраций
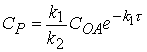
При каких условиях эти выражения совпадают?
Решение:
Сравнивая приближенное выражение
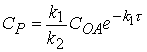
с точным
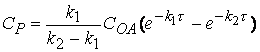
можно
заметить, что эти выражения совпадают, то есть реализуется метод стационарных
концентраций, если ![]() , т.е. первая стадия реакции
, т.е. первая стадия реакции
![]()
является
лимитирующей.
Это условие означает, что промежуточные
частицы очень реакционноспособны, время их жизни мало и, следовательно, их
концентрация мала по сравнению с исходными веществами ![]() (Рис. 17)
(Рис. 17)
|
|
Обратите внимание на
парадоксальность
резуль-
тата
приближенного
решения
при малых значе-
ниях
времени проводе-
ния
процесса - в началь-
ный
момент концент-
рация
промежуточного
вещества
отлична от нуля, что противоречит условию задачи.
|
Рис.17. Сравнение точного
решения зависимости концентрации промежуточного соединения Значения констант скоростей: |
Пример
3.11.
Используя метод стационарных концентраций,
найдите зависимость концентрации конечного продукта ![]() реакции
реакции
![]() ,
,
если ![]() .
.
Решение:
Запишем кинетические уравнения по конечному
веществу
![]()
![]()
и
промежуточному соединению
![]() ,
,
Согласно методу квазистационарных
концентраций скорость по промежуточному веществу можно считать равной нулю:
![]()
Откуда

Но зависимость концентрации вещества А от
времени выражается соотношением
![]() ,
,
которое
подставим в
![]() ,
,
и тогда:
 (4.18)
(4.18)
Полученный результат означает, что скорость
рассматриваемой реакции в квазистационарном режиме зависит только от одной из
констант ![]() .
.
Следовательно, первая - наиболее медленная
реакция - является лимитирующей.
Решение полученного дифференциального
уравнения
![]()
приводит
к соотношению, определяющему зависимость концентрации продукта последовательной
реакции
![]()
от времени
|
|
Сравним точное решение, определяющее
зависимость концентрации продукта последовательной реакции
![]()
|
|
и
решение, полученное в приближении стационарной концентрации промежуточного
вещества:
|
|
|
Рис.18. Зависимость
концентрации продукта в последовательной реакции A -----> B ----->C
|
Сравним относительную погрешность ![]() , которую мы допускаем, используя метод стационарных концентраций
при определении зависимости концентрации продукта последовательной реакции
, которую мы допускаем, используя метод стационарных концентраций
при определении зависимости концентрации продукта последовательной реакции
A -----> B ----->C
от
времени:
|
|
Графическая
иллюстрация приведена на рис.19.
|
|
|
Рис.!(. Относительная ошибка
(отношение A -----> B ----->C;
|
И снова можно отметить, что уменьшение
разности ![]() при том же их
отношении приводит к растягиванию максимума во времени.
при том же их
отношении приводит к растягиванию максимума во времени.
Концентрация промежуточного продукта
длительное время держится приблизительно на одном уровне, близком к
максимальному.
Это действительно дает возможность считать,
что по истечении некоторого достаточно малого времени после начала реакции
устанавливается приблизительно стационарная (квазистационарная) концентрация
неустойчивого промежуточного продукта, сохраняющаяся в течение значительного времени
протекания реакции.
Пример 3.12.
Используя метод стационарных концентраций,
покажите, что реакция
![]() ,
,
протекающая по механизму
2NO<===>![]() (с
константой скорости
(с
константой скорости ![]() в
прямом и
в
прямом и
константой скорости ![]() в
обратном
в
обратном
направлении)
![]() --->
--->![]() (с
константой скорости
(с
константой скорости ![]() )
)
имеет общий третий порядок.
Решение.
Запишем кинетическое уравнение по продукту
реакции
![]() ,
,
где ![]() - концентрация промежуточного соединения, которую,
согласно методу стационарных концентраций, через некоторое время от начала
проведения процесса можно считать приблизительно постоянной.
- концентрация промежуточного соединения, которую,
согласно методу стационарных концентраций, через некоторое время от начала
проведения процесса можно считать приблизительно постоянной.
Тогда скорость по промежуточному веществу ![]()
![]()
Последнее
уравнение дает возможность выразить концентрацию промежуточного соединения ![]() :
:
 ,
,
подстановка которой в
полученное ранее уравнение
![]()
приводит к кинетическому
уравнению по продукту реакции

Анализ этого уравнения показывает, что при соотношении
между константами ![]() >>
>>![]() скорость реакции подчиняется кинетическому
уравнению первого порядка
скорость реакции подчиняется кинетическому
уравнению первого порядка
![]()
и, если ![]() <<
<<![]() , скорость реакции
подчиняется кинетическому уравнению третьего порядка
, скорость реакции
подчиняется кинетическому уравнению третьего порядка

Таким образом, метод квазистационарных
концентраций приводит к существенному упрощению вида кинетических уравнений –
система дифференциальных уравнений
![]() ,
,
![]()
сводится к одному уравнению

Для определения концентрации продукта
реакции в зависимости от времени
проведения процесса, т.е. для интегрирования полученного уравнения,

выразим концентрации
исходных веществ ![]() и
и ![]() через концентрации продукта реакции
через концентрации продукта реакции ![]()
2NO + ![]() <====>
<====> ![]() Исходная концентрация, моль/л
Исходная концентрация, моль/л
![]()
![]() 0
0
Прореагировало к моменту t C ![]() C
C
Концентрация в момент t ![]()
![]() C
C
Подставим в уравнение

концентрации исходных
веществ, выраженные через текущую концентрацию продукта:

Полученное выражение можно
интегрировать.
Если ![]() >>
>> ![]() , то
, то
![]()
и если ![]() <<
<< ![]() , то
, то

Полученные результаты проиллюстрируем примером
решения кинетических уравнений:

при
сравнимых значениях констант скоростей реакций,
при соотношении констант
скоростей ![]() >>
>> ![]()
![]()
и при соотношении ![]() <<
<< ![]()

Результаты
представлены на рис.19.
|
|
Рис.19 Зависимость концентрации продукта
реакции
2NO + ![]() <====>
<====> ![]()
реакция протекает по механизму
2NO<===>![]() (с константой скорости
(с константой скорости ![]() в
прямом и
в
прямом и
константой скорости
![]() в
обратном
в
обратном
направлении)
![]() --->
--->![]() (с
константой скорости
(с
константой скорости ![]() )
)
от
времени проведения процесса.
![]() - константы скорости
- константы скорости ![]() ,
,![]() ,
,![]()
![]() - константы скорости
- константы скорости ![]() ,
,![]() ,
,![]()
![]() - константы скорости
- константы скорости ![]() ,
,![]() ,
,![]()
Начальные концентрации исходных веществ ![]() и
и ![]() моль/л.
моль/л.
Пример 3.13.
Определите константы скорости прямой и обратной реакции изомеризации органического
эфира (обратимая реакция первого порядка, в дальнейшем для краткости ![]() ) при
) при ![]() из следующих
экспериментальных данных по концентрации исходного эфира:
из следующих
экспериментальных данных по концентрации исходного эфира:
начальная
концентрация ![]() моль/л, через 200 часов
моль/л, через 200 часов ![]() моль/л, равновесная
концентрация
моль/л, равновесная
концентрация ![]() моль/л, а в начальный момент времени продукт В отсутствует.
моль/л, а в начальный момент времени продукт В отсутствует.
Решение:
Константа равновесия ![]() определяется из
уравнения:
определяется из
уравнения:

Здесь
![]() моль/л по условию, а
моль/л по условию, а ![]() , где
, где ![]() по условию,
по условию, ![]() моль/л.
моль/л.
Тогда отношение констант ![]() =3,692.
=3,692.
Сумму констант ![]() можно найти,
преобразовав выражение
можно найти,
преобразовав выражение

следующим
образом:

Решая
совместно
![]()
и
![]()
![]() ,
,
находим ![]() ,
, ![]() .
.
Пример 3.14.
Реакция
разложения изопропилового спирта протекает в присутствии катализатора триоксида
ванадия при 588К по схеме:



![]()
Концентрации веществ , измеренные через 4.3с
после начала опыта (ммоль):![]()
Определите константу скорости каждой реакции,
если в начальный момент присутствовал только ![]() .
.
Решение:
Из уравнения материального баланса определим
начальное количество ![]() :
:
![]() ммоль/л
ммоль/л
Кинетическое
уравнение в дифференциальной форме:
![]()
После
интегрирования имеем:

![]()
Далее,
используя соотношение (3.10), получим следующие равенства:


Решая
совместно три последних уравнения, получим
![]()
Пример
3.15
Выведите
выражение для скорости образования продукта реакции
![]()
через
концентрации исходных веществ, используя метод стационарных концентраций, при
следующем механизме реакции:
![]()
![]()
![]()
![]()
![]()
![]()
Решение:
Скорость образования продукта в соответствии с
последней стадией равна
![]()
Промежуточное вещество ![]() принимает участие в
трех стадиях.
принимает участие в
трех стадиях.
Используя метод стационарных концентраций,
приравниваем к нулю скорость образования ![]()
![]()
и
получаем выражение для его концентрации в виде

Следовательно,
скорость образования продукта равна

Метод стационарных концентраций особенно полезен при
анализе предполагаемых кинетических схем сложных реакция.
Рассмотрим это на конкретном примере.
При исследовании кинетики реакции термического
разложения ацетальдегида ![]() было показано,
что скорость образования метана при 673К
описывается кинетическим уравнением
было показано,
что скорость образования метана при 673К
описывается кинетическим уравнением

Исследователи предположили следующий механизм реакции:
Инициирование: ![]() ---
--- ![]() --->
---> ![]()
![]() ---
--- ![]() -->
--> ![]()
Продолжение цепи: ![]() ---
--- ![]() ---->
----> ![]()
![]() ---
--- ![]() --->
---> ![]()
Обрыв цепи: ![]() ------->
-------> ![]()
Исследуем на
основании метода стационарных концентраций, удовлетворяет ли предложенная схема
реакции кинетическому уравнению,
полученному в эксперименте.
Выведем - на основании приведенного
механизма процесса - кинетические уравнения по ацетальдегиду ![]() и оксиду
углерода
и оксиду
углерода ![]() .
.
При анализе
схем многостадийных реакций, на определенных стадиях которых образуются
промежуточные соединения с высокой реакционной способностью, особенно полезен метод
стационарных концентраций,
Условием применимости метода является малое время жизни промежуточных
соединений по сравнению с временем, за которое состав реакционной системы
успевает значительно измениться. Аналитически это означает, что скорость по
этим веществам принимается равной нулю.
Тогда для исследуемой реакции
скорость по метану
![]()
скорость по
оксиду углерода
![]()
скорость по ацетальдегиду
![]()
и скорость по
бензолу
![]()
Во все приведенные уравнения входят концентрации
нестойких промежуточных соединений ![]() и
и ![]() .
.
Воспользуемся
методом стационарных концентраций и запишем кинетические уравнения для
промежуточных соединений.
![]()
![]()
Решим с
помощью символьного редактора MathCAD эту систему уравнений относительно
концентраций промежуточных соединений ![]() и
и ![]() .
.
Из
уравнения
![]()
следует, что
![]()
Подставим
полученное соотношение в уравнение
![]()
и тогда получим уравнение относительно концентрации CH3
![]()
которое решим, используя символьный редактор MathCAD:

Подставим полученное выражение в уравнение
![]()
и определим концентрацию
промежуточного соединения ![]() :
:

Теперь,
подставив полученные выражения концентрации промежуточных соединений в
![]()
определим кинетическое уравнение скорости реакции по
метану в зависимости от концентрации
ацетальдегида:
 ,
,
которое полностью совпадает с полученным в результате эксперимента

Аналогичным образом определим скорость реакции по оксиду углерода,
подставив в уравнение
![]()
концентрацию промежуточного соединения CH2CHO

Тогда получим

И скорость реакции по ацетальдегиду:
![]()
после подстановки
в (20.3) концентрации ![]() :
:

получим кинетическое уравнение

Обратите внимание на полученный результат: скорости
накопления или распада стабильных участников реакции зависят только от текущей
концентрации ацетальдегида.
Таким
образом, получена система дифференциальных уравнений:



![]()
По данным
Е.Т. Денисова (Денисов Е.Т.
Кинетика гомогенных химических реакций. - М.: Высш. школа, 1978, с.151)
константы скорости при 673К соответственно равны: ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Эти данные дают возможность решить систему дифференциальных уравнений, используя встроенную функцию rkfixed , имеющуюся в распоряжении пользователя математического пакета MathCAD.
Вывод результата - зависимость концентраций
участников реакции термического разложения ацетальдегида от времени проведения
процесса при 673К. Начальная концентрация ацетальдегида 0.5 моль/л.
|
|
В матрице u:
U0 – время, с.
u1 - концентрация исходного вещества
ацетальдегида,
u2 - концентрация продукта реакции - метана,
u3 - концентрация продукта реакции -
оксида углерода,
u2 - концентрация продукта реакции - бензола.
Графическая
иллюстрация результатов приведена на рис. 20.
|
|
Рис 20. Зависимость концентраций участников реакции
термического разложения
ацетальдегида от времени проведения
процесса при 673К.
![]() время, с.,
время, с., ![]() - концентрация исходного вещества
ацетальдегида,
- концентрация исходного вещества
ацетальдегида, ![]() -
концентрация продукта реакции - метана,
-
концентрация продукта реакции - метана, ![]() - концентрация продукта реакции - оксида
углерода,
- концентрация продукта реакции - оксида
углерода, ![]() - концентрация
продукта реакции - бензола.
- концентрация
продукта реакции - бензола.
3. ВЛИЯНИЕ ТЕМПЕРАТУРЫ НА СКОРОСТЬ
ХИМИЧЕСКИХ РЕАКЦИЙ
3.1.Уравнение Аррениуса
Скорость реакции зависит не
только от концентрации, но и от температуры. Как показывает опыт, скорость
большинства реакций увеличивается при повышении температуры на 10°С в среднем в
2 ![]() 5 раза.
5 раза.
Приближённой характеристикой зависимости
скорости реакции от температуры является температурный коэффициент реакции
γ, который характеризует отношение константы скорости при температуре(T+10) к
константе скорости при температуре T:
![]() (3.1)
(3.1)
Считая γ
приблизительно постоянным в интервале температур T2 – T1 , можно рассчитать kT2, зная величину kT1:
 . (3.2)
. (3.2)
Это соотношение, называемое правилом Вант –
Гоффа, может быть применимо лишь для приблизительных, ориентировочных расчётов,
поскольку температурный коэффициент изменяется при изменении температуры. Однако
для узкого интервала температур правило Вант – Гоффа часто бывает очень
полезным.
Расчёт показывает, что увеличение скорости
реакции при повышении температуры не может быть объяснено лишь возрастанием
числа столкновений, поскольку не каждое столкновение частиц приводит к
химической реакции.
Лишь
тогда, когда сталкивающиеся молекулы обладают определённой энергией,
столкновение может быть эффективным и привести к химической реакции.
Эти
предположения были впервые высказаны Сванте Аррениусом.
Согласно Аррениусу, к реакции приводит
столкновение лишь тех молекул, энергия которых больше определённой величины,
называемой энергией активации Ea.
Зависимость константы скорости реакции от
температуры Аррениусом была представлена
в виде
 (3.3)
(3.3)
где
k0 –
предэкспоненциальный множитель, не зависящий от температуры;
T – Температура, К;
R – Газовая постоянная (R=8.31 Дж·моль-1·К-1),
Ea
– энергия активации (Дж/моль), равная разности между средней энергией молекул,
способных к активным столкновениям, и средней энергией всех молекул.
Как показывает опыт, величина энергии
активации в достаточно широком интервале температур не зависит от температуры.
Прологарифмируем
уравнение (3.3):

получим
![]() (3.4)
(3.4)
Из (3.4) следует метод экспериментального
определения величины энергии активации: скорость реакции изучают при нескольких
температурах, рассчитывают константы скорости для каждой температуры, строят
график зависимости в координатах (lnk, 1/T).
В
этих координатах рассматриваемая зависимость линейна с тангенсом угла наклона,
равным – Ea/R (рис 21).
Введем
обозначения:
|
|
|
|
|
|
|
|
Рис.21.
Зависимость логарифма константы скорости
![]() реакции
реакции ![]()
от обратной температуры.
Дифференцируя уравнение (3.4)
![]()
по температуре, получим
![]() (3.5)
(3.5)
Величина Ea/(RT2) > 0, поэтому логарифм
константы скорости, а, следовательно, и сама константа с температурой
возрастают, что, впрочем, видно и из (3.3): 

|
Рис.22. Зависимость константы
скорости реакции от температуры. Предэкспоненциальный множитель |
Из (3.5)
![]()
видно, что чем больше величина энергии
активации (если мы, например, будем сравнивать несколько реакций с различными
значениями Ea), тем больше значение производной ![]() , а, значит, константа скорости реакции, имеющей большую
энергию активации, будет возрастать с увеличением температуры быстрее.
, а, значит, константа скорости реакции, имеющей большую
энергию активации, будет возрастать с увеличением температуры быстрее.
Сравним,
например, реакцию
![]() ,
,
предэкспоненциальный
множитель которой ![]() и энергия активации
и энергия активации ![]() и
реакцию
и
реакцию
![]() ,
,
предэкспоненциальный
множитель ![]() и энергия активации
и энергия активации ![]() .
.
Тогда:
 и
и 
и
|
|
|
|
Проследим
влияние температуры на константы скорости исследуемых реакций от обратной температуры (![]() ).
).

Рис.23. Зависимость логарифма константы
скорости
![]() реакции
реакции
![]() (энергия активации
(энергия активации ![]() )
)
и
логарифма константы скорости ![]() реакции
реакции
![]() (энергия активации
(энергия активации ![]() )
)
Из рисунка видно, что, действительно,
константа скорости реакции с большей энергией активации увеличивается с
возрастанием температуры быстрее.
После
интегрирования (3.5)
![]()
от T1 до T2 получим:
 (3.6)
(3.6)
Из (3.6) можно определить величину энергии
активации, если известны значения констант скоростей хотя бы при двух
температурах T1 и
T2.
Заметим, что, поскольку экспериментальное
определение константы скорости производится всегда с некоторой погрешностью,
для более точного определения энергии активации обычно не ограничивается
определением констант только при двух температурах.
Мы рассмотрели один из фундаментальных
законов химической кинетики – закон Аррениуса, устанавливающий зависимость
скорости реакции от температуры:

или
![]()
Объяснения, выдвинутые Аррениусом,
считаются классическими и состоят в том, что в химическую реакцию могут
вступать лишь те атомы и молекулы, которые обладают достаточной энергией для
преодоления потенциального барьера.
Согласно Аррениусу, скорость химической
реакции возрастает с температурой пропорционально множителю ![]() , где
, где ![]() - энергия активации,
т.е. высота потенциального барьера, которые должны преодолеть вступающие во
взаимодействие частицы.
- энергия активации,
т.е. высота потенциального барьера, которые должны преодолеть вступающие во
взаимодействие частицы.
Анализ уравнения Аррениуса позволяет
сделать вывод, что по мере уменьшения температуры скорость всех термодинамически
разрешенных химических реакций должна очень резко снижаться, и вблизи
абсолютного нуля должна исчезнуть – можно сказать, что в этом случае химическая
жизнь должна прекратиться.
Но,
согласно соотношению
![]()
все
экзотермические реакции (![]() ) при температурах, близких к абсолютному нулю,
термодинамически разрешены, поскольку при таких температурах
) при температурах, близких к абсолютному нулю,
термодинамически разрешены, поскольку при таких температурах ![]() .
.
Получается некоторое противоречие –
термодинамика разрешает протекание химических реакций при очень низких
температурах – например, при температурах космического пространства, а кинетика
запрещает, поскольку, согласно Аррениусу, скорость таких реакций должна
равняться нулю.
Противоречие снимается, так как, согласно
законам квантовой механики, переход системы из одного состояния в другое,
отделенное от исходного потенциальным энергетическим барьером, возможно не
только поверх барьера, но и сквозь него – посредством туннельного перехода между
двумя потенциальными ямами.
Вероятность такого перехода резко –
экспоненциально-
убывает
с ростом длины туннеля d и высоты «горы» над
туннелем, т.е. высоты активационного барьера Е.
Скорость туннелирования
 ,
,
где
m – масса частицы.
Было показано, что туннельные переходы
должны стать преобладающими лишь при достаточно низких температурах, ниже
некоторой температуре туннелирования:

Скорость химической реакции при таком
сценарии не становится беспредельно малой величиной, а достигает некоторого
предела, так называемого низкотемпературного предела скорости химической
реакции.
|
|
|
Рис.24 Зависимость логарифма
константы скорости реакции |
В рамках теории Аррениуса зависимость скорости реакции от температуры
означала бы постепенное уменьшение энергии активации и обращении ее в ноль при
очень низких температурах.
Однако потенциальный барьер не меняется с
уменьшением температуры, но при низких температурах все большую роль играет
туннелирование сквозь этот барьер.
Эксперименты по реакции полимеризации
формальдегида при температурах в области от 10К до 4К, показали, что время
роста цепи равно ![]() , тогда как экстраполяция по Аррениусу приводит к значениям
, тогда как экстраполяция по Аррениусу приводит к значениям ![]() лет при 10К и
лет при 10К и
![]() лет при 4К.
лет при 4К.
Вывод: в
условиях космического холода при инициировании космическим излучением могут –
хотя и медленно, но зато верно идти процессы образования самых сложных молекул.
Медленные процессы, направленные в сторону экзотермических реакций,
при сверхнизких температурах могут играть определенную роль в химической и
биологической эволюции.
Экспериментальным подтверждением этих
теоретических предпосылок стало открытие (1975г.) полимеров формальдегида в
межзвездном пространстве и совсем недавнее (2006г.) открытие в межзвездном
пространстве гигантского облака метанола.
3.2. Связь энергии активации с тепловым эффектом реакции
Пусть протекает обратимая реакция
![]()
![]()
Тогда для прямой реакции уравнение Аррениуса

и в дифференциальной форме

Для
обратной реакции

и в дифференциальной форме

Вычитая
из первого уравнения второе, получим

но
константы скорости прямого ![]() и обратного
и обратного ![]() процессов
процессов
связаны соотношением
![]()
где
К – константа равновесия.
Тогда
 (3.10)
(3.10)
Вспомнив,
что
![]() (3.11)
(3.11)
где ![]() – тепловой эффект
реакции, и сравнив (3.10) и (3.11), поучим
– тепловой эффект
реакции, и сравнив (3.10) и (3.11), поучим
![]() (3.12)
(3.12)
Из уравнения (3.12)
![]()
следует, что разность между энергиями
активации прямой и обратной реакции равна её тепловому эффекту.
Величину теплового эффекта
реакции можно рассчитать из термодинамических данных.
Поэтому, определив экспериментально, например,
энергию активации прямой реакции ![]() , мы тем самым по (3.12) можем определить и энергию активации
обратной реакции
, мы тем самым по (3.12) можем определить и энергию активации
обратной реакции ![]() .
.
Анализируя соотношение
![]()
можно
сделать ещё один вывод.
Пусть прямая реакция эндотермична, т.е. ![]() > 0.
> 0.
Тогда
![]()
![]()
Поэтому
 ,
,
а значит, константа скорости
эндотермической реакции будет возрастать с температурой быстрее константы
скорости экзотермической реакции.
В заключение отметим, что энергия активации определяется природой
реагирующих веществ.
3.3. Связь между скоростью реакции и равновесием
Всегда ли выгодно повышать
температуру процесса?
Можно
было бы ответить положительно, поскольку с повышением температуры увеличивается
скорость реакции.
Однако такой ответ не всегда будет верным.
И дело не только в том, что некоторые реакции при больших температурах могут перейти
во взрывные.
Разберём этот вопрос более подробно.
При экзотермической реакции влияние
температуры на константу равновесия и константу скорости противоположно:
константа скорости с увеличением температуры увеличивается
В
соответствии с уравнением Аррениуса
 ,
,
а
константа равновесия согласно уравнению Вант-Гоффа
![]()
уменьшается.
Пусть
протекает экзотермическая (![]() ) реакция,
) реакция,
например, реакция синтеза аммиака
![]()
Константа равновесия реакции равна
 ,
,
где ![]() - равновесные парциальные давления аммиака, азота и водорода.
- равновесные парциальные давления аммиака, азота и водорода.
Причём, как мы уже отмечали, температурная
зависимость константы равновесия определяется уравнением изобары Вант-Гоффа:
![]() .
.
Поскольку ![]() < 0, следовательно, константа равновесия такой реакции с
повышением температуры уменьшается, а значит, и уменьшается выход продукта. Поэтому можно сказать, что при увеличении
температуры в этом случае мы будем получать всё быстрее и быстрее (ведь
скорость реакции увеличивается) все
меньшее и меньшее количество продукта реакции.
< 0, следовательно, константа равновесия такой реакции с
повышением температуры уменьшается, а значит, и уменьшается выход продукта. Поэтому можно сказать, что при увеличении
температуры в этом случае мы будем получать всё быстрее и быстрее (ведь
скорость реакции увеличивается) все
меньшее и меньшее количество продукта реакции.
Другими словами, при достаточно высоких температурах равновесия достигается быстро, но
продукта реакции образуется очень мало.
Поэтому возникает задача поиска оптимальной температуры, при которой
достигается достаточно глубокое превращение и приемлемая скорость процесса.
Алгоритм такого поиска рассмотрим на
конкретном примере.
В случае эндотермических реакций константы
скорости и константа равновесия увеличиваются.
Способ увеличения скорости
реакций, свободный от подробного рода ограничений, связан с применением
катализаторов.
Пример 3.16.
Для обратимой реакции первого порядка
A <===>B
изменение энтальпии при
298К ![]()
Константа равновесия ![]() .
.
Зависимость константы
скорости прямой реакции от температуры
описывается соотношением:

Начальная концентрация вещества A ![]() .
.
Продукт реакции В в начальный момент отсутствует.
При различном времени протекания реакции определите температуру Т, при которой степень превращения исходного вещества c максимальна.
Решение.
Поскольку рассматриваемая реакция - обратимая реакция первого порядка, то ее
кинетическое уравнение
 ,
,
где ![]() и
и ![]() - константы скорости прямой
- константы скорости прямой ![]() и обратной
и обратной ![]()
реакции.
В соответствии с соотношением
![]() ,
,
связывающим текущую
концентрацию ![]() вещества А с его начальной концентрацией
вещества А с его начальной концентрацией ![]() и степенью превращения c, уравнение
и степенью превращения c, уравнение

можно записать как

После несложных
преобразований получим:

Для обратимых реакций константы скорости
прямой ![]() и обратной
и обратной ![]() реакции связаны с константой равновесия
соотношением
реакции связаны с константой равновесия
соотношением

Подставим в предыдущее уравнение:

и после упрощений получим

По условию задачи константа
скорости прямой реакции зависит от температуры

Зависимость константы равновесия от
температуры (в приближении, что в области температур 298-Т температура не
влияет на изменение энтальпии реакции)
выражается уравнением:

Следовательно, задача сводится к расчету
константы равновесия К и константы скорости прямой реакции ![]() при различных температурах, подстановке их
значений в дифференциальное уравнение
при различных температурах, подстановке их
значений в дифференциальное уравнение

и его решению.
Ниже
представлены результаты решения (с помощью встроенной функции ![]() ,имеющейся в математическом
пакете MathCAD) при трех температурах и
графическая иллюстрация полученных результатов.
,имеющейся в математическом
пакете MathCAD) при трех температурах и
графическая иллюстрация полученных результатов.
|
|
Решение дифференциального уравнения
(кинетического уравнения в дифференциальной форме обратимой реакции первого
порядка A<===>B)

при температуре 298К.
В
нулевом столбце - время, с., в первом столбце - степень превращения
исходного вещества при соответствующем значении времени протекания процесса.
|
|
Решение дифференциального уравнения
(кинетического уравнения в дифференциальной форме обратимой реакции первого
порядка A<===>B)

при температуре 318К.
В нулевом столбце - время, с., в первом столбце - степень превращения c исходного вещества при соответствующем значении времени протекания процесса.
|
|
Решение дифференциального уравнения
(кинетического уравнения в дифференциальной форме обратимой реакции первого
порядка A<===>B)

при температуре 338К.
В нулевом столбце - время, с., в первом столбце - степень превращения c исходного вещества при соответствующем значении времени протекания процесса.
|
|
Рис.25.
Зависимость степени превращения c от времени протекания процесса в обратимой экзотермической реакции первого
порядка при различных температурах.
![]() - температура 298К,
- температура 298К, ![]() -
318К,
-
318К, ![]() -
338К,
-
338К, ![]() время,
с.
время,
с.
Расчеты показывают, что наши
теоретические предположения, сделанные на основе анализа температурных
зависимостей константы скорости и константы равновесия обратимой
экзотермической реакции оказались справедливыми:
при достаточно высоких температурах равновесия достигается быстро, но
продукта реакции образуется очень мало.
Способ увеличения скорости реакций,
свободный от подробного рода ограничений, связан с применением катализаторов.
Если обратимая реакция эндотермична
(![]() ) ,
т.е. протекает с поглощением тепла, то и константа скорости – в соответствии с уравнением
Аррениуса
) ,
т.е. протекает с поглощением тепла, то и константа скорости – в соответствии с уравнением
Аррениуса

и
константа равновесия – в соответствии с изобарой Вант- Гоффа

увеличиваются.
В этом случае повышение температуры благоприятно
сказывается на сдвиг равновесия в сторону продуктов реакции и скорость процесса.
4. КИНЕТИКА ГЕТЕРОГЕННЫХ РЕАКЦИЙ
4.1. Общие понятия
Многие промышленные процессы
основаны на реакциях, протекающих на границе раздела фаз. Такие процессы
называются гетерогенными.
Кинетика гетерогенных процессов
характеризуется рядом особенностей, отличающих её от кинетики гомогенных
процессов.
Гетерогенные реакции обычно представляют
сложный процесс, который состоит из ряда последовательных стадий:
1)
подвод реагентов к поверхности раздела, на которой происходит химическая
реакция;
2)
химическая реакция;
3)
отвод продуктов реакции.
Если
один из реагентов – твёрдое пористое вещество или твёрдый катализатор, то кроме
перечисленных стадий, процесс может быть осложнён диффузией реагентов в порах твёрдого тела к его
внутренней поверхности, адсорбцией исходных веществ и продуктов реакции.
Поэтому скорость гетерогенных процессов
зависит не только от химических свойств системы, но и от её физических свойств,
влияющих на скорость массопереноса между фазами.
Одним из таких свойств является величина
поверхности раздела фаз S.
Скорость гетерогенных процессов обычно
пропорциональна поверхности раздела, например, для реакции первого порядка A®B
![]()
Поверхность раздела фаз, а, следовательно, и
скорость процесса, могут быть увеличены дроблением твёрдых веществ или
разбрызгиванием жидкости.
Обычно для характеристики гетерогенных
процессов вводят понятие удельной скорости ![]() , т.е. скорости реакции, отнесённой к единице поверхности.
, т.е. скорости реакции, отнесённой к единице поверхности.
Другим таким свойством является перенос
реагентов к поверхности раздела, что является одной из обязательных стадий
гетерогенного (и, в частности, гетерогенно – каталитического) процесса.
Если химическая реакция, т.е. реакция на
поверхности, протекает быстро, то скорость суммарного процесса может
лимитироваться подводом реагентов к внешней поверхности частиц, а для пористого
тела – ещё и диффузией реагентов внутрь пор.
Скорость реальных гетерогенных процессов
зависит и от скорости собственно химической реакции на поверхности, и от
условий массопереноса. Раздел кинетики, изучающий реакции, скорость которых осложнена
процессами переноса вещества, называют макрокинетикой.
Иногда
скорость одной из стадий (подвода реагентов или химической реакции) много
меньше другой, причём настолько меньше, что она определяет, или, как говорят,
лимитирует скорость процесса в целом.
В качестве примера приведём данные скорости
горения углерода в воздухе при различных температурах и скоростях воздушного
потока (рис. 4.1).
Из рис. 4.1 следует, что при
сравнительно низких температурах
скорость реакции не зависит от скорости подачи воздуха. Следовательно, при
таких температурах лимитирующей стадией является скорость химической реакции,
тогда как при повышенных температурах (скорость химической реакции с
температурой резко возросла и стала намного выше скорости подвода воздуха)
лимитирующей стадией становится скорость транспорта реагентов.
4.2. Макрокинетика. Внешнедиффузионная область
При протекании гетерогенной
реакции у границы раздела создаётся тонкий слой, внутри которого концентрация
меняется от её значения в объёме Cv до её значения на
поверхности Cs. Этот слой обычно называют диффузионным слоем.
Перенос вещества через такой слой определяется законами молекулярной диффузии.
Согласно первому закону Фика, количество
вещества, диффундирующее за единицу времени ![]() через поверхность S,
пропорционально поверхности S, коэффициенту диффузии D и
градиенту концентраций
через поверхность S,
пропорционально поверхности S, коэффициенту диффузии D и
градиенту концентраций ![]() (x –
координата, направленная по нормали к поверхности):
(x –
координата, направленная по нормали к поверхности):
![]() . (4.1)
. (4.1)
Знак минус означает, что при ![]() > 0 поток вещества направлен к поверхности.
> 0 поток вещества направлен к поверхности.
Если
градиент концентрации постоянен в пределах диффузионного слоя толщиной ![]() , то (4.1) превращается в (4.2) с учётом
, то (4.1) превращается в (4.2) с учётом ![]() :
:
![]() (4.2)
(4.2)
Тогда,
с учетом определения скорости гетерогенного процесса как количества вещества,
реагирующего в единицу времени на единице поверхности, скорость диффузии rs, ДИФ может быть выражена
соотношением
![]() (4.3)
(4.3)
Отношение D/δ называют константой
скорости диффузии.
В дальнейшем
будем обозначать D/δ = kД.
![]() Анализ уравнения
Анализ уравнения
приводит к выводу: если скорость гетерогенного
процесса лимитируется диффузией реагента к внешней поверхности (в этом случае
говорят, что процесс протекает во внешнедиффузионной области), то независимо от
механизма химической реакции на поверхности кинетика ее подчиняется уравнению
первого порядка по концентрации в объеме.
Скорость процесса во внешнедиффузионной области слабо зависит от температуры: это
определяется в свою очередь слабой зависимостью от
температуры коэффициента диффузии D:
 (4.4)
(4.4)
где Eа, диф - энергия
активации процесса диффузии.
Причем, если для химических процессов
величина энергии активации обычно составляет 40-120 кДж/моль, то энергия
активации диффузии обычно составляет 8-12 кДж/моль и практически не зависит от
природы реагирующих веществ. Малое значение Eа, диф и приводит к слабому влиянию температуры на
скорость протекания процесса во внешнедиффузионной области.
Более сильный эффект на скорость
процесса во внешнедиффузионной области оказывает перемешивание, что связано с
влиянием перемешивания на толщину диффузионного слоя:
 (4.5)
(4.5)
где w — скорость
движения реагентов относительно поверхности раздела фаз.
Отсюда
 (4.6)
(4.6)
Отметим, что при протекании реакции в кинетической
области, когда скорость определяется реакцией на поверхности, перемешивание не
оказывает воздействия.
Полученные
закономерности могут служить критериями протекания реакции во
внешнедиффузионной области, что очень существенно.
Если
на скорость процесса существенное влияние оказывает перемешивание или процесс
характеризуется малым температурным коэффициентом, то лимитирующей стадией
такого процесса является подвод реагентов к поверхности раздела, т. е. процесс
протекает во внешнедиффузионной области.
Пусть
на непористой поверхности, все участки которой одинаково доступны для диффузии
реагентов из объема, протекает мономолекулярная реакция по приповерхностной
концентрации
![]()
Кинетика такой реакции описывается соотношением
rS = kCS. (4.6)
Скорость
диффузии в соответствии с (4.3)
rS,ДИФ = kД(CV – CS). (4.7)
В стационарных условиях скорость химической реакции
и скорость диффузии равны:
kCS
= kД(CV – CS). (4.8)
Из (4.8) найдем СS и подставим в (4.7):
 (4.9)
(4.9)
или
 .
.
Если константа скорости реакции много
больше константы скорости диффузии, т. е. k>>kД, то
rS = kДCV. (4.10)
Если kД>>k, то
rS = kCV. (4.11)
В первом случае процесс протекает во
внешнедиффузионной области с константой скорости, равной константе скорости
диффузии, характеризуется малой величиной энергии активации, обычной для
процессов диффузии.
Во втором случае процесс лимитируется
химической реакцией, протекает в кинетической области с константой скорости,
равной константе скорости химической реакции, имеет энергию активации,
характерную для химических реакций.
Если k![]() kД, то процесс протекает в так называемой переходной
области. В этом случае для него характерны особенности и химической кинетики и
диффузионных процессов. Энергия активации обычно имеет промежуточное значение
между энергией активации химической реакции и энергией активации диффузии.
kД, то процесс протекает в так называемой переходной
области. В этом случае для него характерны особенности и химической кинетики и
диффузионных процессов. Энергия активации обычно имеет промежуточное значение
между энергией активации химической реакции и энергией активации диффузии.
4.3. Макрокинетика. Внутридиффузионное торможение
Обычно
при протекании гетерогенных процессов в системе газ – твёрдое тело или жидкость
– твёрдое тело, твёрдое тело (в том числе и катализатор) часто имеет пористую
структуру с развитой внутренней поверхностью. Для достижения участков
внутренней поверхности реагенты должны продиффундировать к ней сквозь поры.
Если скорость диффузии в порах соизмерима со
скоростью химической реакции на стенках
пор, то говорят, что процесс протекает во внутренней диффузионной области,
которая характеризуется своими особенностями.
В этой области протекания процесса скорость
подвода реагентов к поверхности твёрдого тела превышает скорость реакции.
Поэтому концентрация на поверхности Cs не отличается от
концентрации в объёме. Однако внутренние участки активной поверхности могут не
принимать участия в реакции благодаря замедленности диффузии реагентов внутрь
пор. Для этой области существенно то, что при изменении скорости реакции
меняется глубина работающего слоя.
Задача о кинетике реакций во
внутридиффузионной области была впервые решена Я.Б. Зельдовичем (1939 г.).
В наиболее простом случае это задача о
диффузии в бесконечный слой пористого тела, которое рассматривается как
квазинепрерывная среда, характеризуемая эффективным коэффициентом диффузии Dэф.
Приведём только краткие выводы, которые
следуют из решения этой задачи.
Эффективная константа скорости реакции равна
![]() , (4.12)
, (4.12)
где
n – порядок реакции;
k – удельная константа
скорости реакции.
Поскольку Dэф
относительно
мало зависит от температуры, а величина k меняется с температурой по
уравнению Аррениуса, энергия активации реакции (её обычно называют кажущейся
или эффективной энергией активации)
 (4.13)
(4.13)
т.е.
при протекании процесса во внутридиффузионной области кажущаяся энергия
активации вдвое меньше энергии активации в
кинетической области, а порядок реакции – средний между истинным (т.е.
порядком реакции в кинетической
области) и первым.
Глубина проникновения реакции во внутрь
пористого тела зависит от эффективного коэффициента диффузии, константы
скорости и удельной поверхности:
 , (4.14)
, (4.14)
где
SV – удельная поверхность единицы объёма пористого
тела.
Наблюдаемая скорость реакции оказывается
пропорциональной квадратичному корню из истинной константы скорости.
В частном случае для химической реакции,
протекающей по первому порядку,
 , (4.15)
, (4.15)
где
CS - концентрация реагента поверхности пористого тела;
Cx – концентрация в глубине
пористого тела на расстоянии x от поверхности;
L – глубина проникновения
реакции, или расстояние от поверхности, на котором концентрация снижается в е
раз.
4.4.
Заключение
Что же даёт исследователю знание кинетики
химических реакций?
Знание кинетики реакции позволяет рассчитать
концентрацию реагирующих веществ в любой момент времени, предсказать время, в
течение которого реакция пройдёт на определённую глубину, целенаправленно
изменять условия протекания реакции для того, чтобы она протекала с необходимой
скоростью и необходимой степенью превращения.
Другими словами - знание кинетики реакции открывает возможность
управлять ею.