НЕДОКУМЕНТИРОВАННАЯ СИМВОЛЬНАЯ
МАТЕМАТИКА Mathcad/Maple
(Коробов В., Сясев А.
– приложение 2 к пятому тому справочника >>>>>>>)
П2.3. Недокументированная матричная алгебра
в Mathcad
П2.4. Интерпретатор команд Maple
Оговоримся
сразу, что материал этой главы предназначен для пользователей, уже имеющих
определенный опыт работы с пакетом. Остальных просят не беспокоиться, во всяком
случае, не следует начинать работать с книгой именно с этой главы. Речь пойдет
о недокументированных возможностях пакета Mathcad.
Как
уже говорилось, символьные вычисления в среде Mathcad стали
возможными после того, как разработчики внедрили в нее символьное ядро системы Maple и цивилизованно узаконили это внедрение, о чем можно
узнать из закладки командного меню Help|About Mathcad (рис. П2.1).
Кроме этого, на рис. П2.1
приведена несколько необычная символьная конструкция kernelopts(version),
возвращающая сообщение о том, из какой именно версии пакета Maple был
заимствован символьный процессор. Никаких сведений о функции kernelopts в руководстве
пользователя не содержится, однако, как видим, она с успехом работает в среде Mathcad. Естественное любопытство подсказывает, не
попробовать ли в среде Mathcad применить
другие «чисто мэйпловские» команды и функции. Современные версии Maple насчитывают,
как известно, более трех тысяч встроенных функций, в то время как количество
встроенных функций Mathcad не превышает полутора сотен. Вот
и возникает соблазн расширить диапазон применимости системы Mathcad.

Рис. П2.1. Информация о встроенном в Mathcad символьном
ядре Maple
Нужно
сказать, что вопрос о допустимости использования недокументированных приемов
весьма спорный. Сторонники концепции так называемого «культурного
программирования» считают, что недокументированными приемами пользоваться
нельзя категорически - ни в каких-либо пакетах, ни в программировании вообще.
Например, такого мнения придерживаются многие авторы книг компьютерной
тематики. Другие занимают несколько более мягкую позицию. К ним относятся, в
том числе и разработчики системы Mathcad. Пользоваться недокументированными приемами они не запрещают,
но и не рекомендуют их, объясняя отсутствие рекомендаций тем, что гарантий
правильной работы той или иной недокументированной команды, процедуры или
функции они не дают, поскольку их работа не тестировалась. Некоторые функции,
родившиеся в системе Maple, при переходе к новым версиям становятся документированными. Например,
в Mathcad 12 обрела официальный статус функция time(), находившаяся до этого на полулегальном положении. Между прочим, прием
использования тандема операторов `:=` и `→` до сих пор остается недокументированным, несмотря на
то, что он приобрел внушительную популярность у пользователей. Этот «тандем» операторов
в 13-й версии Mathcad стал давать сбои. Многие недокументированные функции,
успешно работавшие в предыдущих версиях, частично «глушатся» разработчиками в
версиях последующих. Возможно, это делается из соображений оптимизации объема
ядра, но не исключены и какие-то другие причины: «Фирма Mathsoft купила
у фирмы Waterloo Maple (http://www.waterloomaple.com)уздечку.
Пришла домой, глядь – а к уздечке привязана лошадь». В
12-й и 13-й версиях лошадь вернули хозяину с извинениями. А вот версия Mathcad 11 осталась этаким симбиозом лошади в виде
символьного ядра Maple с трепетной ланью в лице Mathcad. И хотя известная поговорка гласит, что запрячь этих
представителей фауны в одну упряжку весьма проблематично, тем не менее, Mathcad 11 можно назвать на сегодняшний день версией с потенциально наиболее
обширным арсеналом для проведения аналитических вычислений среди всех других
версий.
Недокументированные
приемы не рекомендуется применять и потому, что последствия такого применения
могут быть непредсказуемыми. Прежде всего, это относится к правильности
получаемых результатов расчета. Возможно также и «зависание» компьютера, и
внезапное без всякого предупреждения закрытие программы без сохранения
информации.
Итак,
следует помнить, что попытка применить недокументированную функцию или прием
может быть чревата неприятностями. Конечно, эти неприятности не такие уж
серьезные, как те, что согласно мифологии
принесла миру когда-то Пандора, открывшая ящик (по другим источникам -
сосуд), который открывать не следовало, но определенные аналогии напрашиваются.
Те,
кто работал с системой Maple, хорошо знают, что она предназначена главным образом
для проведения аналитических (символьных, символических) вычислений. Если пользователю
необходимы исключительно вычисления
этого рода, то ему, естественно, лучше работать с этой системой. На сегодняшний
день Maple считается одной из лучших систем компьютерной
алгебры. Но как быть пользователю Mathcad, если в его
работе наряду с численными расчетами все же значительное место занимают
символьные преобразования? Особенно это касается случаев, когда создаются
документы Mathcad образовательного характера. Одно дело, когда ведется
расчет по какой-либо готовой формуле. Совсем другое – когда нужно показать,
каким образом это уравнение выводится, исходя из физической картины изучаемого
процесса или явления. Ясно, что иметь на компьютере две системы – роскошь,
которая большинству пользователей, мягко говоря, не по карману. Это одна из
причин, пробуждающая интерес к расширенному использованию символьного ядра Maple в среде пакета Mathcad.
Кстати,
проявлять любопытство к недокументированным приемам подталкивают пользователя
сами разработчики. На рис. П2.1a приведены
некоторые примеры символьных вычислений, проведенных в среде Mathcad 11. Исходные конструкции для всех примеров на рис.П2.2 заданы вполне корректно,
в полном соответствии с принятыми в Mathcad правилами. Результат же вычислений является в
достаточной степени неожиданным для пользователя: как видим, в ответах
содержатся конструкции Beta, EllipticF, EllipticPi, StruveL, Sum, RootOf, &where, о смысле
которых можно только догадываться, поскольку никаких сведений на этот счет
справочная система Mathcad не
дает. Зато исчерпывающий ответ относительно происхождения этих конструкций
находится в help’е пакета Maple.
Простейшие
недокументированные приемы работы в режиме символьных вычислений показаны на
рис. П2.3. Как видим, к
операциям дифференцирования и взятия неопределенного интеграла вполне применим
синтаксис, принятый в Maple. Кроме того, на рис. П2.3
можно увидеть и некоторые абсолютно чуждые в Mathcad команды, тем не менее, успешно работающие в среде
пакета. Оказывается, можно работать отдельно с числителем и знаменателем
выражения (команды denom,
numer),
обращаться к конкретному операнду выражения (команда op), узнать число операндов в выражении (nops).
Кстати,
на рис. П2.3 скрыта первая
неприятность, которую даже опытный пользователь заметит не сразу. Обратим
внимание, что в результате работы команды op(f’(x)) был сгенерирован вектор из трех элементов,
следовательно, верхняя двойка в этом векторе с позиций языка Mathcad является
нулевым элементом, поскольку по умолчанию установлено нулевое значение
системной переменной ORIGIN. Чужеродная же команда op(1,f’(x)) считает эту двойку не нулевым, а первым операндом
исходного выражения, ведь в Maple по умолчанию
нумерация элементов массивов начинается с единицы, а не с нуля. Это обстоятельство
обязательно следует учитывать, если по каким-либо причинам потребуется
недокументированная обработка массивов.
Популярная
среди пользователей символьная команда simplify далеко не всегда выдает результат в желаемой
пользователю форме. Казалось бы, логарифм произведения на экране выглядел бы
более компактно, нежели сумма логарифмов, тем не менее, символьный редактор Mathcad/Maple именно
последний вариант записи рассматривает как максимально упрощенный. По каким-то
причинам разработчики символьного ядра сделали так (а, может быть, что-то
сделали не так), что применение команды simplify далеко
не во всех случаях приводит к наиболее короткой и лаконичной форме выражения.
Иногда приходится искусственно подправлять результат, производя «ручные»
упрощения так, как это подсказывают навыки, приобретенные на школьных уроках
алгебры. Особенно явно это проявляется при создании различных документов
образовательного характера: хочешь получить уравнение, которое по форме
совпадает с приведенным в учебнике, но не тут-то было.
Оказывается, очень хорошим помощником в этом деле может выступить
недокументированная функция combine. На рис. П2.4
проведено сравнение результатов работы этой функции с документированным приемом
упрощения через simplify. Нужно признать, что такое сравнение явно не в пользу simplify: получаемые с помощью combine конструкции имеют более компактный и законченный вид.
При работе с combine
пользователю необходимо указывать
дополнительные опции в зависимости от типа исходного выражения: опции atan, trig позволяют символьному ядру в полной мере проявить свои
знания тригонометрии, опция power
позволяет быстро разобраться с
показателями степеней для одной переменной. А вот для того, чтобы «собрать» все
логарифмы выражения под единый логарифм, необходимо указать вместе с опцией ln дополнительную характеристику symbolic.
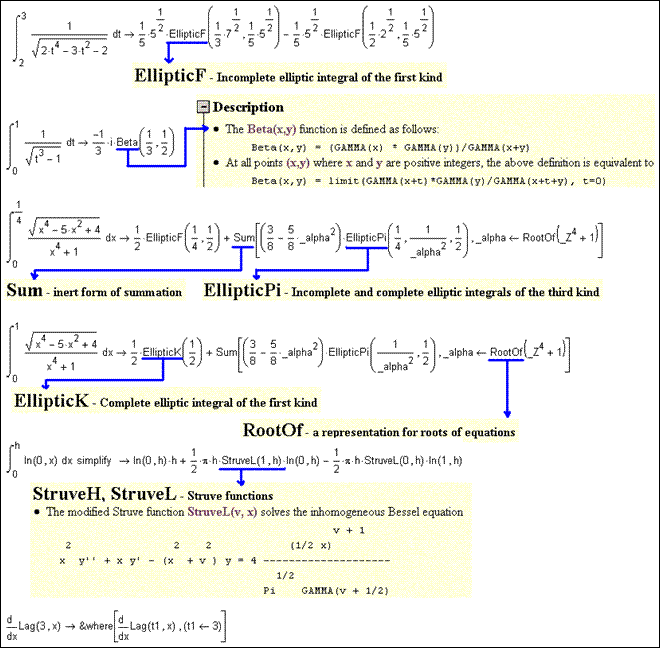
Рис. П2.2. Примеры необычных результатов работы символьного
редактора Mathcad

Рис. П2.3. Простейшие примеры недокументированных приемов
работы в режиме символьных вычислений
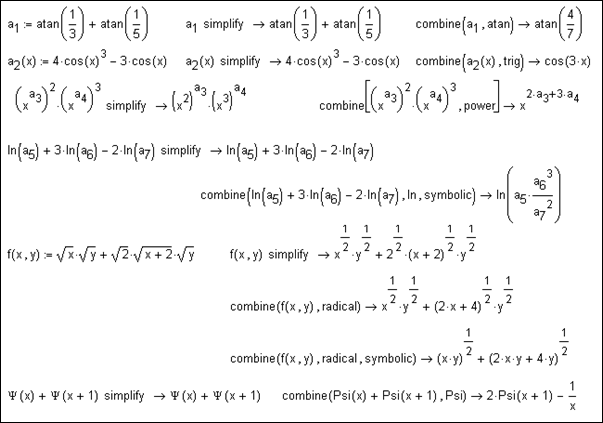
Рис. П2.4. Недокументированная команда combine
Конкретная
польза команды combine видна из рис. П2.5, который содержит решение
двух задач из области химической кинетики. В первой части документа средствами
символьного редактора выводится кинетическое уравнение для автокаталитической
реакции на основе ее математической модели, представленной в виде довольно
простого дифференциального уравнения с разделяющимися переменными при заданных
начальных условиях. Традиционное решение дает правильный, но слишком уж
громоздкий результат. Двукратное применение команды combine позволяет
существенным образом «причесать» интегральную форму кинетического уравнения.
Второй фрагмент документа на рис. П2.5
вообще может показаться странным. С точки зрения синтаксиса Mathcad такое
безалаберное применение операторов локального присваивания недопустимо, и
система реагирует на такой произвол пользователя тем, что «зажигает» красный
цвет в соответствующих конструкциях. Но цель такого подхода состоит в том, что,
как ни странно, именно операторы присваивания численного значения помогают
«запомнить» результаты промежуточных символьных расчетов и использовать их в
последующих конструкциях. В данном случае недокументированный
Mathcad позволяет понять, что обобщенное кинетическое
уравнение для реакции порядка n справедливо и
для реакции первого порядка. Для этого необходимо раскрыть неопределенность по
правилу Лопиталя. Раскрытие неопределенности также проведено
недокументированным приемом, основанном на обращении к числителю и знаменателю
дроби. До сих пор остается непонятным, почему функциям denom и numer разработчики
не придали статус документированных.
Пожалуй,
в наибольшем разнообразии проявляет себя Maple-функция convert, предназначенная для
конвертирования символьных выражений в ту или иную форму, выбранную
пользователем. Кстати, англо-русский политехнический словарь
переводит слово convert как: а) преобразовывать;
превращать; переводить (единицы, меры); 2) переоборудовать, перерабатывать.
В «традиционном» Mathcad функция эта
вроде бы находится на вполне легальном положении, о чем говорит, например, рис.П2.6. На самом деле в Mathcad узаконено только применение этой функции лишь с
единственной опцией – parfrac. Maple, тем не менее, предоставляет целый сонм опций для функции convert, и недокументированное
использование этой функции в полной мере дает представление о ее мощи.
Начнем
с размерностей. Пользователь системы Mаthcad даже
не подозревает о том, что кроме встроенных единиц измерения она имеет и скрытые
размерности, проявляющие себя только в том случае, если пытаться достучаться до
символьного ядра недокументированными средствами. Одной из многих опций функции convert является
опция metric,
позволяющая преобразовывать многие единицы измерений в точном соответствии с
переводом, который дает англо-русский словарь (рис. П2.7). В метрическую систему функция convert переводит более 50 единиц измерения, среди которых, в
основном, единицы массы, длины и объема. Пользователь Mathcad,
не прибегая к услугам Maple, может, в
частности, получить представление о том, что собой представляет бушель (bu, bushel, bushels) и чем, например, американская (US) пинта (pint, pints) отличается от пинты британской (imp). Также можно выяснить, какое
расстояние проходит свет за год (light_year) и т.д. Обратим внимание, что все приведенные имена
единиц размерностей, указанные в теле функции convert первыми, не зарезервированы в Mathcad. При численных расчетах система Mathcad диагностирует
их как переменные, которые не определены.
В версиях Mathcad 2000, 2001, 2001i, 11 вполне доступны операции представления выражения expr в форме form с помощью символьной конструкции
(option –
дополнительные опции)
convert(expr,form,option)→
Рис. П2.8 в полной мере дает представление о возможностях
символьной функции convert: пользователь может заранее для себя выбрать именно
ту форму представления символьной конструкции, которая для него более удобна и привычна,
а не полагаться целиком только на разрешенные документацией возможности редактора символьных преобразований. Здесь и
различные формы представления одних специальных функций через другие, и
представление чисел в различных системах счисления, а также множество других
способов конвертирования выражений, недоступных в традиционном
документированном Mathcad.
На
форуме пользователей Mathcad (http://forum.exponenta.ru/viewforum.php?f=1) однажды был задан вопрос о том, каким образом можно
преобразовать матрицу в вектор. Было предложено несколько вариантов ответа,
каждый из которых предусматривал формирование программного блока. Подобный
пример можно найти и в центре ресурсов пакета Mathcad (соответствующая программа приведена на рис. П2.9), хотя операцию
преобразования матрицы М в вектор-столбец гораздо проще провести с помощью
недокументированной функции convert(M, vector).
Считается,
что Mathcad
не имеет средств символьного решения
дифференциальных уравнений и систем дифференциальных уравнений. Это
действительно так, если не брать во внимание возможность аналитического решения
уравнений с разделяющимися переменными (только пользователь обязан
предварительно разделить эти переменные). Кроме того, можно решать линейные
дифференциальные уравнения, а также системы линейных ОДУ с помощью
документированных символьных функций laplace, invlaplace. Эти функции реализуют специальный математический
аппарат преобразования Лапласа, позволяющий с применением определенных приемов
свести дифференциальное уравнение или систему ОДУ к алгебраическому уравнению
или системе алгебраических уравнений. Далее модифицированное уравнение или
система решается традиционными средствами (функция solve или
с помощью решающего блока GIVEN…FIND). При этом приходят к так называемому операторному
решению. Операторное решение играет сугубо вспомогательную роль и подлежит
последующему конвертированию в решение настоящее, окончательное, согласно
правилам обратной Лаплас-трансформации. Именно эти
положения реализует документ, приведенный на рис. П2.10. По большому счету, его уже трудно назвать
документом Mathcad,
поскольку в нем наряду с традиционными приемами реализованы и
недокументированные возможности интегральных преобразований. Задача,
приведенная на рис П2.10,
также относится к области химической кинетики и посвящена аналитическому
решению системы обыкновенных дифференциальных уравнений, которая является
математической моделью последовательности двух необратимых реакций первого
порядка. Обратим внимание, что в приведенном документе функция laplace, на первый взгляд,
применена вообще вне соответствия синтаксису Mathcad. Тем не менее, документ вполне работоспособен в
версии Mathcad 11.
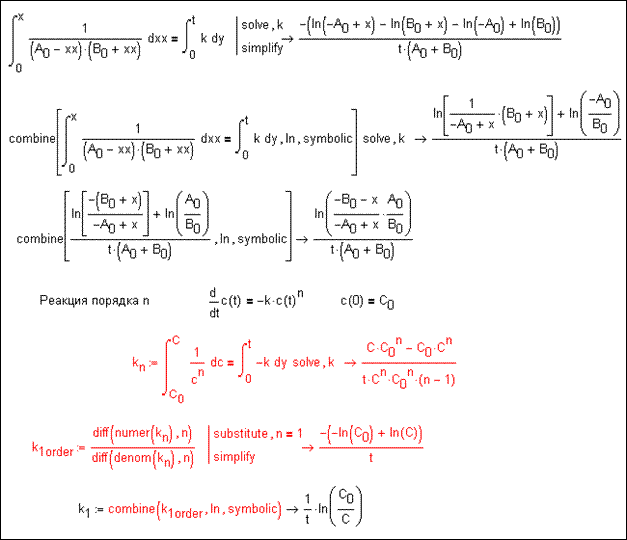
Рис. П2.5. Недокументированное решение двух задач
химической кинетики

Рис.П2.6. Ключевое
слово parfrac как одна из опций функции convert

Рис. П2.7. Работа функции convert с опцией metric

Рис. П2.П2. Недокументированное использование функции convert

Рис. П2.8а (продолжение)

Рис. П2.8. (продолжение)

Рис. П2.9. Недокументированное конвертирование матрицы в
вектор
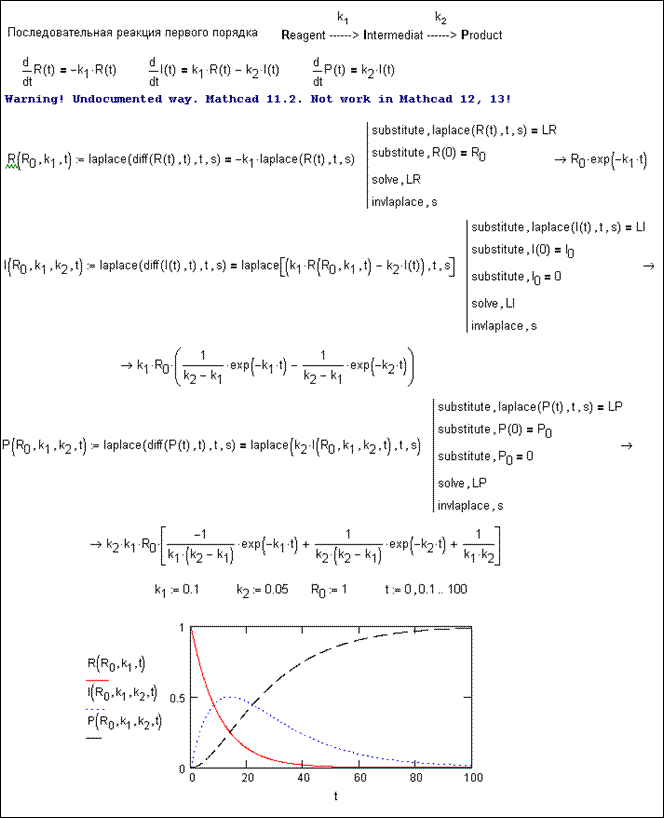
Рис. П2.10. Недокументированное символьное решение системы
дифференциальных уравнений
Противники
недокументированных приемов будут активно возражать против такого варварского в
определенном смысле документа, который помещен на рис. П2.10. Во многом они будут правы, хотя бы потому, что
приведенный в таком варианте документ какой-то мере утратил свою
универсальность: он будет корректно работать только в версиях Mathcad 2000 – 11. По этой причине нелишне подобные документы
сопровождать остерегающим комментарием типа «Минздрав
предупреждает, что злоупотребление недокументированными средствами… и т.д.».
Конечно, правильнее было бы искать в любой задаче документированные пути
решения. Нет подходящей встроенной функции – пишем соответствующий программный
блок. Но в том-то и дело, что основным притягательным признаком системы Mathcad является
ее демократичность в том смысле, что Mathcad изначально
не требует от пользователя каких-либо глубоких знаний в области
программирования. Многие пользователи не имеют таких знаний и навыков и, строго
говоря, не обязаны их иметь в силу своей основной профессиональной
деятельности. Не секрет, что основная масса пользователей – это не
программисты. Профессиональные программисты вряд ли будут использовать в своей
деятельности Mathcad, когда
есть куда более мощные программные среды. Те же, кто использует пакет Mathcad на
промежуточном этапе решения конкретной прикладной задачи, могут столкнуться с
ситуацией, когда именно на этой стадии исходная задача переходит из плоскости
конкретной отрасли знаний в область программирования, да так, что пользователь
на достаточно долгое время отвлекается от конечной цели. В конце концов,
назначение любого математического пакета – облегчить жизнь пользователю. Пусть,
например, в ходе решения какой-либо задачи, будь то из области физики, химии,
геологии или другой дисциплины возникла эпизодическая проблема – а является ли
число, ну, скажем, 12371, простым? Подчеркнем, что проблема именно
эпизодическая, но без ее разрешения невозможны дальнейшие рассуждения. Как
быть? Начать заниматься написанием специальной вспомогательной программы, целью
которой будет выяснение мелкой детали в цепи решения более глобальной задачи?
Можно, конечно, потратить некоторое время на составление такой программы, а
потом сожалеть о том, что это время было потрачено зря, узнав, что в символьном
ядре уже давно дремлет готовая процедура, предназначенная для диагностики
простых чисел. Следующий недокументированный прием показывает, что число 12371
не является простым:
isprime(12371) → false
Кстати, многие
недокументированные функции успешно работают и на Mathcad Application Server. На рис. П2.11
показан WebSheet (http://twt.mpei.ac.ru/MAS/Worksheets/prime.mcd), демонстрирующий работу недокументированных функций isprime, prevprime, nextprime.

Рис. П2.11. Недокументированные функции
на сервере MAS
П2.3.
Недокументированная матричная алгебра в Mathcad
Система
Maple имеет
мощнейший арсенал процедур и функций для работы с векторами и матрицами,
Возможность использования этих функций появляется при загрузке библиотеки linalg (рис. П2.12). Пользователь легко может убедиться в том, что
подавляющее большинство из приведенного на рис. П2.12 списка функций вполне комфортно чувствуют себя в
среде Mathcad 11. Но одновременно
он должен решить для себя, нужны ли они ему в таком количестве. Некоторые из
них уже имеют законную прописку в Mathcad (augment, cholesky, diag, rank, eigenvals, rref, matrix и
т.д.), некоторые имеют своих Mathcad-аналогов и оформлены в виде специальных элементов
интерфейса (det, inverse, transpose). Некоторые функции имеют различные имена в обеих
средах, но работающие при символьных вычислениях абсолютно одинаково (например,
вряд ли есть необходимость при решении систем линейных уравнений функцию lsolve заменять недокументированной linsolve). Свыше полусотни функций не имеют аналогов в Mathcad, но работают в этой среде, около двух десятков –
вроде бы на первый взгляд неработоспособны, но дополнительными ухищрениями им
можно придать работоспособность (см. раздел П2.5).
Не
будем утомлять читателя полным списком примеров работы недокументированных
«векторно-матричных» функций. Такой список можно посмотреть на сайте http://twt.mpei.ac.ru/ochkov/Sovet_MC/086/Tip_86_eng.htm.
Заметим при этом, что многие из этих функций могут быть весьма полезными при
будничной работе с массивами (рис. П2.13).
Предположим, что имеется матрица A, в которой все элементы первого столбца (с1) нужно умножить на некоторое число m, затем поэлементно просуммировать столбцы c1 и c2 и, наконец, в столбец c2 поместить полученные суммы. Конечно, все сказанное
можно без особого труда реализовать разрешенным, документированным
инструментарием, но оказывается, что все эти операции одним махом может
проделать недокументированная функция addcol(A,c1,c2,m). Примерно такую же модификацию матрицы А, но уже в
отношении строк, выполняет функция addrow(A,c1,c2,m). Иногда пользователю может понадобиться создание
различных типов блочных матриц (BlockMatrix, JordanBlock), различного рода вставки одной матрицы в другую (copyinto), изменение основной
матрицы путем одновременного добавления в нее определенного количества новых
строк и столбцов (extend), генерирование матриц и векторов, элементами в которых являются
случайные целые числа (randmatrix, randvector) и т.д. Действительно, стоит ли отвлекаться каждый
раз на формирование специальных матричных конструкций документированными
средствами, если таковые уже «дремлют» в недрах символьного ядра, и их можно
заставить работать? Проще иметь отдельный документ с примерами работы недокументированных
функций и обращаться к тем или иным из них по мере надобности. Здесь, правда,
может проявить себя уже упоминавшийся эффект пандориного ящика: из символьного
ядра-ящика вылезают все новые и новые функции, от них уже рябит в глазах. Более
того, одна и та же функция может применяться с различными дополнительными
опциями – вспомним, хотя бы уже рассмотренную функцию convert. «Функции начинают расползаться, как тараканы», если
перефразировать известного литературного героя, активно гонявшегося за стульями
воробьяниновской тещи.
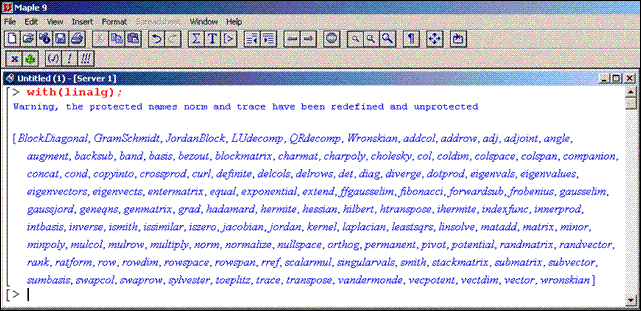
Рис. П2.12. Команды и функции Maple-библиотеки linalg
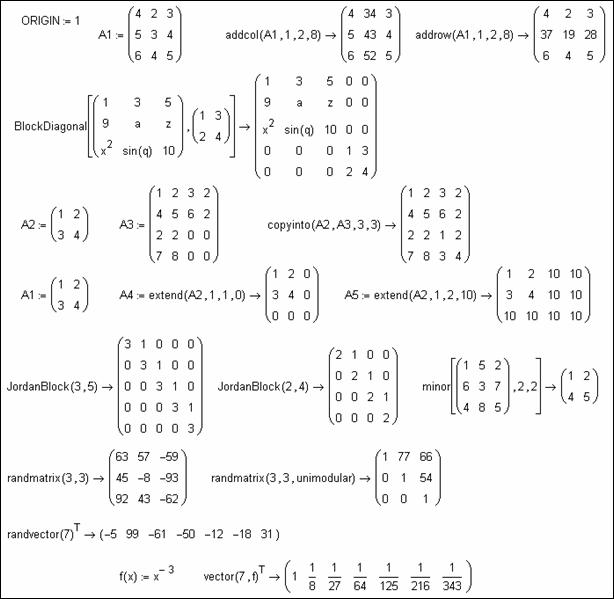
Рис. П2.13. Недокументированная работа с векторами и
матрицами
П2.4.
Интерпретатор команд Maple
Так
какие же функции символьного ядра Maple «работают» в среде Mathcad 11? Вряд ли можно ответить на этот вопрос. Ответа на
него, наверное, не дадут и сами разработчики Mathcad. Одно можно сказать точно: коль в Mathcad встроено
ядро Maple V Release 4, то бесполезно
пытаться обращаться к тем функциям, которые появились в более поздних версиях
пакета Maple. Но даже ядро Maple V содержит сотни функций и команд. В основном это
команды и функции стандартной библиотеки, а также библиотек линейной алгебры (linalg) и интегральных
преобразований (inttrans).
Команда
addressof(имя функции)
позволяет узнать, отведено ли в памяти компьютера определенное место для
конкретной функции. Если в результате выполнения этой команды возвращается
какое-либо численное значение, то данная функция присутствует в символьном
ядре. В противном случае выдается ошибка «No symbolic result
found», т.е. искомой функции в
символьном ядре просто-напросто нет, а, значит, пытаться ее применять не имеет
смысла. Пользователя, почувствовавшего вкус к недокументированным приемам, ждет
большое разочарование, когда он узнает об отсутствии в недрах Mathcad/Maple мощнейшего
инструментария для аналитического решения дифференциальных уравнений и систем в
лице функции dsolve (рис. П2.14). Надо признать, что наличие
именно этой функции весьма существенным образом расширило бы возможности пакета
Mathcad 11. Впрочем, если команда addressof и возвращает какое-либо число, то это отнюдь не
обозначает, что указанная в ее теле функция будет выполняться (см., например,
безуспешную попытку применения недокументированной функции piecewise на рис. П2.14).
Причин этому две: либо функция «заглушена» разработчиками, либо доступ к ней
противоречит синтаксису Mathcad. Так, при формировании вычислительных конструкций Mathcad нельзя
пользоваться клавишей пробела, поскольку такая конструкция тут же превратится в
текстовый комментарий. Нельзя также при недокументированной работе вводить
символы точки, «обычного равно», квадратных и фигурных
скобок и т.п. Все эти символы, являющиеся неотъемлемым элементом многих
конструкций языка Maple, в Mathcad выполняют
совершенно иную роль. По этой причине, например, недокументированными
средствами нельзя провести аналитические вычисления определенных интегралов,
пределов, т.е. нельзя применить функции, задание параметров
в теле которых находится в противоречии с синтаксисом системы Mathcad. Эту проблему частично решает программный блок,
предложенный В.Н.Мезенцевым (рис. П2.15).
Эта вспомогательная программа, по сути, является интерпретатором команд Maple. Если ее загрузить в начале документа Mathcad, то диапазон применимости недокументированных функций
существенным образом расширяется. Главный «фокус» программы в том, что
символьная вычислительная конструкция представляется в виде переменной типа string, чем обеспечивается относительное «примирение»
синтаксисов Mathcad
и Maple. Далее благодаря функции parse (также недокументированной) такая конструкция
становится «понятной» для выполнения символьным редактором.

Рис. П2.14. Команда addressof

Рис. П2.15. Программный блок - интерпретатор команд Maple
Уже говорилось о том, что
документы Mathcad
могут с успехом использоваться сферой
образования. Посмотрим, например, как с помощью вспомогательной программы,
показанной на рис. П2.15,
можно наглядно продемонстрировать, что из собой представляет сплайн-функция как
совокупность специальным образом построенных многочленов. В документе на рис. П2.16 использованы возможности
недокументированной функции spline c
различными возможными опциями (linear, quadratic, cubic, quartic), указывающими на выбранную степень многочленов при
интерполяции сплайном. Результатом символьных вычислений являются конкретные
выражения для различных полиномов для всех интервалов между узлами
интерполяции.
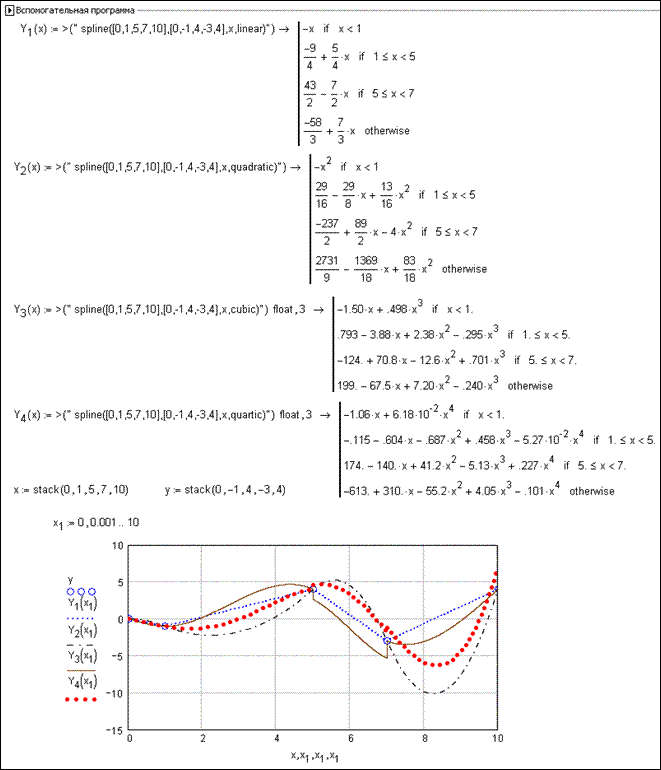
Рис.П2.16.
Проведение сплайн-аппроксимации через
недокументированную функцию spline
В
наборе встроенных средств Mathcad для численного
решения жестких дифференциальных уравнений и систем имеются функции Stiffb, Stiffr (см. главу 5). Определенные неудобства, а то и серьезные трудности
при работе с этими функциями возникают из-за необходимости формирования матрицы
Якоби J(t,x) для функции-вектора f(t,x)
правой части (частей) дифференциального уравнения (системы дифференциальных
уравнений). Причина в том, что аргументы t и x неравнозначны, если так можно выразиться, по своему
смыслу и синтаксису: t – имя
независимой переменной, а x – это имя вектора искомых функций, каждая из которых
обозначается соответствующим индексом этого вектора. Символьное или численное
вычисление матрицы Якоби (якобиана) сопровождается операцией дифференцирования
как по независимой переменной t, так и по переменным x0, x1 …xn в зависимости от общего числа интегрируемых функций. Пакет Mathcad же весьма
болезненно реагирует на попытку пользователя применить эту операцию к индексной
переменной. Неопытный пользователь очень часто наталкивается на диагностическую
ошибку «The
expression to the left on the equal sign cannot be defined» и… прекращает
возиться с непонятным интегратором типа Stiffb.
Возможно, именно из-за этого или в том числе из-за этого версия Mathcad 2001i была пополнена новой функцией для решения жестких
систем Radau, отличительной особенностью которой стало то, что в
списке ее параметров отсутствовал якобиан. Все же прежние интеграторы были
оставлены, поскольку в некоторых случаях они дают более точные результаты
расчета, чем Radau (плата за простоту).
На
рис. П2.17 показан способ
формирования якобиана для функции вектора правых частей жесткой системы ДУ.
Документированное определение, как видим, сопровождается необходимостью
промежуточной модификации этого вектора, хотя он определен в полном
соответствии с синтаксисом системы Mathcad. Для этого
ранжированные индексы у переменных убираются. Далее пакету фактически
приходится растолковывать, что именно представляет собой якобиан системы ДУ и
только после этого искомым переменным снова даются их исконно родные имена.
Такой порядок действий громоздок и неуниверсален, поскольку стоит изменить
число элементов исходного вектора правых частей СДУ, как снова приходится
начинать все сначала. С этой точки зрения более лаконичным и выигрышным
смотрится недокументированный прием и использованием Maple-функции jacobian из библиотеки linalg.
Символьный процессор в данном случае совершенно спокойно реагирует на попытку
дифференцирования функции по переменной, являющейся элементом массива.
Единственный элемент дискомфорта доставляет необходимость контроля числа
открытых и закрытых скобок, поскольку в этой ситуации Mathcad отреагирует на
скобочный дисбаланс не своим обычным «This expression hase a “(” without “)”», а просто отмахнется от пользователя уведомлением «No symbolic result was
found», мол, все вопросы к Maple и
его символьному ядру.

Рис.П2.17. Расчет
матрицы Якоби для жесткой системы ОДУ: сравнение недокументированного и
документированного приемов
В
заключение приведем еще один пример эффективности применения
недокументированных приемов. В задаче о гусях (см. раздел 2.4) уже применялась
недокументированная функция isolve для
поиска целочисленных корней (нулей) уравнения. В то же время существуют задачи,
требующие целочисленного решения систем алгебраических уравнений. Значительную
часть таких задач составляют задачи подбора коэффициентов в уравнениях
химических реакций. Каждый изучавший химию в школе или вузе сталкивался с такой
ситуацией. Химики-профессионалы, конечно, никогда не прибегают к услугам
компьютера для того, чтобы «уравнять» реакцию. Считается, что каждый уважающий
себя химик должен уметь это делать и без ПК. Для этого существует масса
приемов, базирующихся на составлении электронного или электронно-ионного
баланса. Более того, важным показателем «химической» квалификации является
умение писать реакционную схему, исходя только из совокупности реагирующих
веществ, т.е. умение определить, какие именно продукты могут образовываться в
ходе того или иного взаимодействия. Тем не менее, существуют схемы превращений,
подбор коэффициентов для которых превращается в весьма рутинное мероприятие с
большой вероятностью ошибки при ручных вычислениях. Одним из наиболее
экзотических примеров является окисление комплексного соединения хрома
перманганатом калия, которое в кислой среде протекает по схеме:
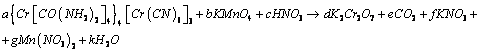
Оставим в покое представления
о балансе ионов и электронов и попробуем подобрать коэффициенты к этой реакции,
исходя лишь из балансовых соотношений химических элементов, входящих в состав
веществ-участников процесса. Нетрудно увидеть (рис. П2.18), что такие балансовые соотношения образуют
систему уравнений, количество неизвестных в которой в данном случае ровно на
единицу больше, чем количество самих уравнений. Следовательно, система имеет
бесконечное множество решений. Химическому смыслу соответствует набор ненулевых
целочисленных значений a, b, c, d, e, f, g, k, и при этом их сумма должна быть минимальной. Как
видим, традиционное документированное применение символьных вычислений с
использованием блока GIVEN/FIND, в общем-то,
решает задачу, но нужное решение получено несколько искусственно: результат
умножается на 10 и делится на a. Попытка же численного решения вообще терпит фиаско: Mathcad пытается
либо подсунуть нулевые значения коэффициентов (что, между прочим, не лишено
смысла: если исходных веществ не брать, то никаких продуктов, разумеется, не получим),
либо выдает нецелочисленные решения, да и то только после того, как в решающий
блок вставлены соответствующие неравенства-ограничения. Зато
недокументированный прием с использованием функции isolve проявляет себя с наилучшей стороны. Ситуация значительно
усложняется, если пытаться решать документировано систему уравнений, в которой
количество неизвестных превышает количество уравнений на 2. В этом случае имеем
«бесконечное число бесконечных наборов» целочисленных коэффициентов и
разобраться с нужными решениями становится проблематично. Между тем в химии и
такая ситуация отнюдь не редкость. Примером может быть окисление перекиси
водорода тем же перманганатом. Заинтересовавшемуся читателю предлагается самому
убедиться в том, что для этой реакции справедливы, например, следующие наборы
коэффициентов:
2 KMnO4 + H2O2 + 3 H2SO4
→ 2 MnSO4 + 3 O2 + K2SO4 + 4
H2O,
2 KMnO4 + 1443 H2O2 + 3
H2SO4 → 2 MnSO4 + 724 O2 + K2SO4
+ 1446 H2O;
2 KMnO4 + 200003 H2O2 +
3 H2SO4 → 2 MnSO4 + 100004 O2
+ K2SO4 + 200006 H2O и т.д.

Рис. П2.18. Применение недокументированных средств для расстановки коэффициентов
в уравнении
окислительно-восстановительной реакции