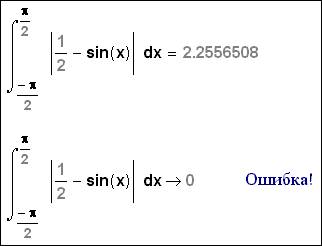V.Ochkov – http://twt.mpei.ac.ru/ochkov
5.1. Coordinate system the diagram
The foreword
This article – collateral product of work of the author above two books of a series «Mathcad for the professionals»: «Tips fore Mathcad users» and «Dimensions in Mathcad ». In heat of work above the books the new version Mathcad – Mathcad 2001 has appeared. But not a final (commercial) product, and beta-version. It has required to bring in corrective amendments in described above of the book. Previously author had to study novelties Mathcad 2001, as has joined given article.
So, what new!
1. Panels (Palette) of tools and menu
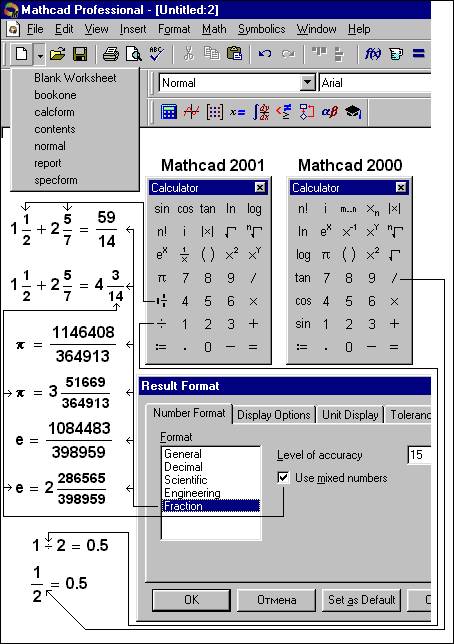
The acquaintance with Mathcad 2001 begins, naturally, with the menu and from panels of buttons – “dubbing actors” of the most popular commands of the menu, which occur on the screen of the display after start of a package, after an input (entrance) on Mathcad 2001 – see fig. 1:
Fig 1. Panels of buttons Mathcad 2001
Here is only one novelty – one change: to the right of the button of creation of the new Mathcad-document the button of opening the list of patterns has appeared. Earlier (Mathcad 7, 8 and 2000) this list could be open on the screen only through a command New … from the menu File.
As to panels of tools, the changes
have touched only panel Calculator: in a fig. 1 this
panel is showed in «two editions» – in edition Mathcad 2000 and in edition Mathcad 2001.
That it is possible to note new in
the panel Calculator:
·
The button of input in account of mixed fraction has
appeared. Now in Mathcad it is possible to work not only with decimal, but also
with simple fractions and not only with an invisible symbol of multiplication (2×a and/or 2a), but also with
an invisible symbol of addition: between the whole and fractional parts of
expression entered into account by the new operator, there is an invisible mark
of addition (see the
article “Invisible Variable” – http://twt.mpei.ac.ru/ochkov/Invisible/Eng/Index.htm).
In pair with the new operator of mixed fraction the new option of formatting of
the numerical answer – see
dialogue box «Result Format» in a fig. 1 works: now fractional answer can be
output not only as decimal fraction with a floating point, but also as simple
Fraction, allocating or not allocating thus a fractional part (see tick at the
signature Use mixed number – to use mixed number). As simple fraction it is
possible to output meaning (importance) of two basic mathematical constants:
numbers π and e (basis of the natural logarithm) – see fig. 1. But this
opportunity rather disputable: Here it is better to receive not the answer as
simple or mixed fraction, and message on a mistake. And that at the user can
develop impression, that the developers Mathcad have solved a problem, above
which the
best minds (wits) of mankind during several a thousand years – representation of
number ð as simple fraction (problem similar to a problem “quadrature of a
circle”) were beaten. Decimal fraction at us, as a
rule, associates with the limited accuracy, and simple – with absolute (compare
0.333 … and 1/3). In a fig.
1 number π and å the numerators and which denominators of integers
are output as fraction: nevertheless answer is limited in accuracy to 15 marks
in a mantissa. If this number to reduce (see field with this number in a
dialogue window in a fig.
1), and the output numerical value π and å will vary in appropriate
way.
·
The alternative operator of division ¸,
allowing to conduct this arithmetic action in one line, has appeared still in
Mathcad 2000. In Mathcad 2001 these operators can be entered not only through a
chord [Ctrl + /], but also through the appropriate button on the panel
Calculator. To two built-in operators of division («two and the one-storeyed
division») if necessary is possible to add and two user. In a fig.
1à is shown, as it can be made:
Fig 1a. User’s operators of division
Symbols "/" and ":" it is possible to enter into account as symbols of the operators of division, having muffled a chord [Shift+Alt+k] work of the same keys as macro of input of the operator of division and operator of giving. After that the cursor will change the colour with dark blue on red, that will be an attribute of a textual mode of input of special symbols. Repeated pressing this chord returns dark blue colour to the cursor.
·
On the panel Calculator the button 1/x has appeared.
It, as well as button ¸, does
not enter in Mathcad the new operator, and simply duplicates, accelerates input
in account of the old operator returning return value of an operand.
·
On the panel Calculator Mathcad 2001 after input of
three new buttons there were same 25 buttons: from the panel have removed
buttons m … n (Range Variable –
"undervector"), Xn (an
n-st element of a vector) and X-1
(return matrix or scalar). Now these buttons have remained only on the panel of
work with matrixes.
2. New machine arithmetics
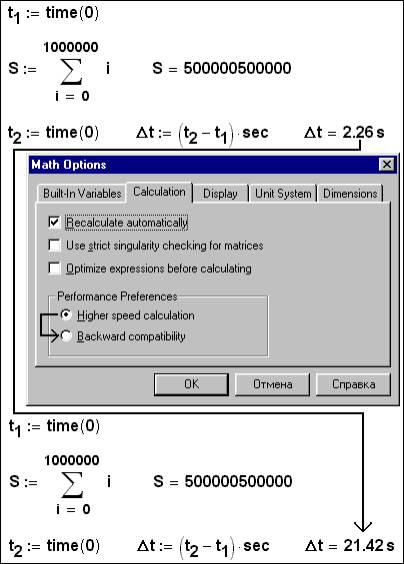
This key novelty Mathcad is not displayed in any way externally in the menu or on panels of tools (see fig. 1), but it can very essentially affect work in Mathcad. The point is that Mathcad is a program interpreting, instead of compiling class. Because of it the account even under the not so big sheet (on the separate "advanced" functions – odesolve, for example, the decision of a boundary task in the field of the differential equations) can last rather long. In Mathcad 2001 by default the account is "forced" – see radiobutton in the frame Performance Preference of a dialogue box Math Options, caused by a command Options … in the menu Math (fig. 2):
Fig. 2. New opportunities of calculations in Mathcad 2001
In a fig. 2 the comparison usual and accelerated ("forced") arithmetics Mathcad on the elementary task – summation of numbers of a natural number in a range from one up to one million is carried out. The answers of usual and accelerated arithmetics (higher speed calculation), as well as it is necessary to expect, it have turned out identical (500000500000), but the difference in time of the account has appeared essential: accelerated arithmetics Mathcad works almost on the order faster (2.26 against 21.42 seconds). The not documentary Mathcad-function returning an operating time of system in seconds is involved in tests displayed in a fig. 2. In itself this time does not interest us, but the difference of times (Dt) can essentially help to carry out high-speed tests of the programs.
In a fig. 2 it is possible to see the old opportunity of acceleration of the account. It is «Optimize expression before calculating »: in this case account is anticipated by the analysis and simplification of expression by means of symbolical mathematics Mathcad, more correctly, Maple. In our case the simplification of the sum gives expression, account on which to last shares of second – see fig. 2à:
Fig 2a. Optimization of the account through symbolical transformation
To the right of the optimized formula there is a red
six-coal asterisk. In Russia speak, that it is a hint that the best mathematics
are the Soviet Jews (joke: What is a American university? It is a place, where
the former Soviet Jews teach mathematics Chinese).
But farly from being all tasks can
be solved by means of symbolical mathematics. Moreover, analytical answer all
the same to have to finish by numerical methods (calculation under the
formulas, construction of the diagrams, search of roots of the equations etc.
etc.). Here "forced" arithmetics Mathcad very much to be useful. To
be useful as well such advice: before a series of calculations with attraction
of "forced" arithmetics one of points should be counted «on a silent
course» and to compare results with «by a fast course».
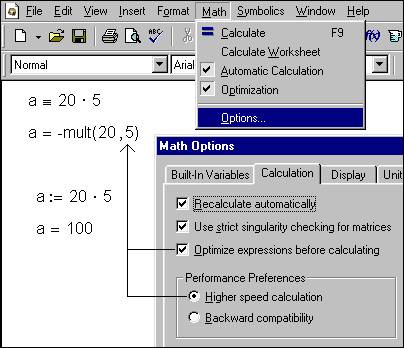
Fig. 2b. Mistake of “fast" mathematics by optimization of numerical accounts
Accelerated arithmetics Mathcad can be disconnected –
see button Backward compatibility (compatibility with the old versions). This
opportunity (« returning to old ») realizes a known principle « Not up to fat –
to be I would live! »: the developers Mathcad have left and
"cruising" (not "forced") speed of the account for those to
whom result, instead of speed is important. Besides the new tool frequently
contains mistakes. One such mistake is shown in a fig. 2b: variable entered by
global assignment operator inadequately behaves at multiplication, when the
modes Optimize and High speed calculation are simultaneously included.
3. Check on singularity
In slangy of speech such check frequently name,
pardon, «check on lousiness». The experienced users not only Mathcad, but also
other computing systems have set of examples « putting these computing systems
on a place ». A pier, as that system is clever and quickly does not
consider(count), but at me in a stock is example, which once again show, that
the man (that is, me) all the same remains by king not only alive, but also
lifeless nature. If to return to optimization of calculations through
analytical transformation illustrated in a fig. 2a, it
is possible to show, that such optimization can not accelerate, and slow down
accounts. A concrete example – certain integral, where the top and bottom
limits are equal. The man and calculus mathematics Mathcad at once «will
"think", that such integral is equal to zero. The symbolical
mathematics Mathcad at first « will be long and persistently » to search
antiderivative intergrand of expression and only then (at substitution of
limits) "will think", that for any antiderivative to search would not
follow. This example allows to depict features of the "human" and
machine account: skilled mathematics frequently it happens of enough fluent
sight to solve a task – to understand, for example, that this equation has no
roots, and given matrix singular etc. etc. by Such examples the users of
mathematical packages «to thrust nose» of the developers, reproaching them in
faults.
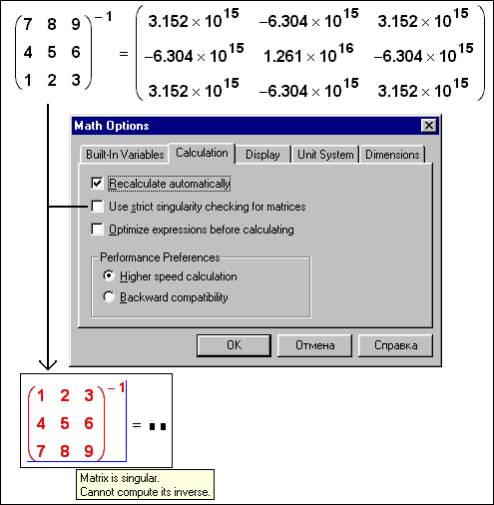
The Singular matrix lays at the users of computers under a hand in a literal sense are buttons on numerical ("small") keyboard of the computer. This matrix the users Mathcad frequently "palm off" on a package, asking it to calculate a return matrix – see first operator in a fig. 3:
Fig. 3.
Work with singular matrix
Usual Mathcad to "shame" will calculate a matrix, opposite singular. In environment(Wednesday) Mathcad 2001 these operations can be anticipated « by check on singularity – Use strict singularity checking for matrices» (see. a fig. 3). In this case calculation of a return matrix will interrupt by the message on a mistake (see last operator in a fig. 3). The similar message, by the way, occurs and in "old" Mathcad at attempt of calculation of a return matrix by means of symbolical mathematics. The symbolical mathematics Mathcad, more correctly, Maple too makes mistakes – see fig. 3a.
Fig. 3a. Error in Symbolic Math
Analytical «check on lousiness» (once again, I ask to forgive for slangy expression) is applied now and to scalar calculations. An example – x • lg(x) at x = 0. Earlier Mathcad gave out here zero (erroneous) answer, and now (Mathcad 2001) – message on a mistake (“This Function is undefined at one or more of points you specified”).
But concerning all these "mistakes" of the developers of computing systems it is possible, well if not to justify then to understand. In Mathcad 2001, for example, there was such mistake: sin (0)/0 gives a zero in the answer, instead of message on a mistake («Division by zero»). The point is that with the purposes of the same acceleration of accounts (see item 2) is considered, that the product is equal to zero, if first is equal to zero efficient.
The developers Mathcad, creating computer arithmetics, are "pressed" between the requirements of accuracy, faultlessness both speed and requirements rationality of system from the point of view of its cost and terms of creation. Yes, it is possible to let out on the market faultless software, which "faultlessness" will be achieved at the expense of its very high price and low speed. Such product can not find the buyer.
Example with the singular a matrix "highlights" to us the very interesting tendency in development of computing systems: the computing systems should be able not only solve the put tasks with acceptable accuracy and with acceptable speed, but also to be able to do the preliminary analysis of a soluble task.
In three above mentioned examples three directions of development Mathcad are illustrated:
1.
Qualitative changes: the operator was not, and in the
new version it has appeared (fig. 1).
2.
Quantitative changes: the speed of the account has
increased (fig. 2).
3.
Correction of mistakes or removal of some
restrictions. The third direction concerns and to the fourth novelty Mathcad
2001.
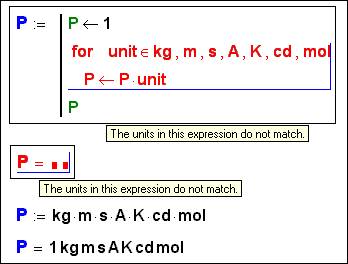
4. Units in Program
In Mathcad 2001, as the
developers assure, the problem of units in cycles, alternatives and other
designs varying the natural order of performance of the operators is solved.
In Mathcad 6-2000 Pro in shoulders of alternative was admitted to have values of one type – or dimensionless, or one dimension. The deviation (rejection) from this rule interrupted by the message on a mistake – see first half of fig. 4, where the work of function if is shown and operator if. In Mathcad 2001 these restrictions are taken off (see second half of fig. 4).

Fig. 4. Alternative with Units
Business with the operator return,
preschedully interrupting performance of the program was more difficultly.
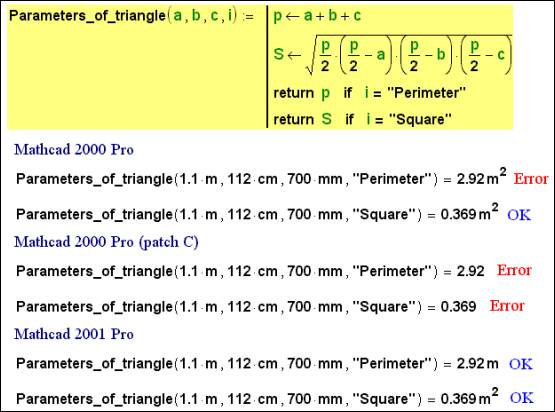
Fig. 5. Corrections in work of function return
In a fig. 5 the creation and work of function returning or perimeter, or area of a triangle is shown depending on value of the fourth argument (first three arguments – length of the parties of a triangle). Mathcad 2000 Pro is confused in these three parties of a triangle «as in three pains». Originally in Mathcad 2000 Pro the program-created function returned the correct numerical answer (2.92 and 0.369 if to speak about conditions of a task shown in a fig. 5), but incorrect units of perimeter (m2 instead of m). In July, 1999 has appeared the patch C (second patch for Mathcad 2000 Pro), which has resulted that the function in a fig. 5 in general has ceased to give values without units at the initial data with units. In Mathcad 2001 the given mistake is eliminated. But all the same defects remain. So still parameter of a cycle cannot accept values of various physical sizes – see fig. 6.
Fig. 6. Mistake or restrictions at work with dimensions in a cycle Mathcad
It is connected that is considered
(is conceived so), that the cycle with parameter in Mathcad chooses value for
parameter of a cycle from a vector. And the vector (array) is an assembly
especially “same dimensions” of elements. In a fig. 6 is
not present any physical sedition (revolt – there is a
product all of seven basic units SI), but, nevertheless, performance of the
program interrupts by the message on a mistake. Use of units the programs is
braked also by that the programs very much frequently work with vectors and
matrixes, which still can store only dimensionless or "same
dimensions" values.
In a fig. 6 the not documentary method – task of parameters of a cycle for as the list is used. The documentation Mathcad permits here to use only Range Variable or Vector. In a fig. 6a is shown, what consequences can take place at a support on the not documentary method.

Fig. 6a. Features of a cycle for in Mathcad
2001
In a fig. 6a
by a program way the product of first seven simple numbers is calculated off. A
variable cycle for accepts values from the list (2, 3, 5, 7, 11, 13,17) – from
a number of numbers shared by points. In
Mathcad 2000 this not documentary reception passed, and in Mathcad 2001 – already is not present. It is
necessary to replace the list with a row vector. But the row vector is not a
vector, and matrix with one row. Leaves so, that we again use the not
documentary reception: the vector (2 3 5 7 11
13 17) needs to be unwrapped on 90 degrees (to transpose).
5. New Functions
5.1. Coordinate system the diagram
In Mathcad 2000 the opportunity has appeared to change system of coordinates of the three-dimensional diagram with rectangular (Cartesian) on cylindrical and spherical. This change of coordinates was conducted and is conducted through radiobuttons (Options) of a bookmark General of a dialogue box of formatting of the three-dimensional diagram. The author used this opportunity for drawing complex volumetric figures ("apple" and "vase") under the simple formulas – see gallery the three-dimensional diagrams Mathcad – http://www.mathsoft.com/mathcad/library/3Dplots.
In
Mathcad 2001 it is possible to make transformations of coordinates of the
diagrams not only visually, but also "mathematically" with the help
of new functions returning coordinate of points in new system of coordinates:
sph2xyz(v), sph2xyz(r, q, f), cyl2xyz(v), cyl2xyz(r, q, f), xyz2sph(v), xyz2sph(r, q, f), xyz2cyl(v), xyz2cyl(r, q, f), pol2xy(v), pol2xy(r, q, f), xy2pol(v) & xy2pol(r, q, f)
5.2. New smoothing function
In Mathcad (since 7-th version, if the author is not mistaken) there is a function genfit, allowing to solve a task "«general" smoothing (fitting). General in the sense that smoothing (approximating) the equation theoretically can be the equation of any kind with any number of required factors.
But for many users Mathcad this function remains some
«by the Chinese letter» with not clear sense and way of a call. The function genfit requires (demands) as
argument not only smoothing function with arguments – elements of a vector, but
also partial derivative of this function on various required factors. In Mathcad 2000 function genfit has
"scattered" on a number of functions deciding approximate a task on
separate functions: expfit(vx, vy, vg),
lgsfit(vx, vy, vg),
logfit(vx, vy, vg),
pwrfit(vx, vy, vg)
and sinfit(vx, vy,
vg), where the smoothing function looks like: a*e^(b*x)+c, a/(1+b*e^(-c*x)), a*ln(x+b)+c, a*x^b+c
è a*sin(x+b)+c accordingly. In Mathcad 2001 these lines
is complemented new by function lnfit (x, y)
(smoothing function –
a*ln (x) +b). The work of function lnfit
(x, y) is shown in a fig. 7:
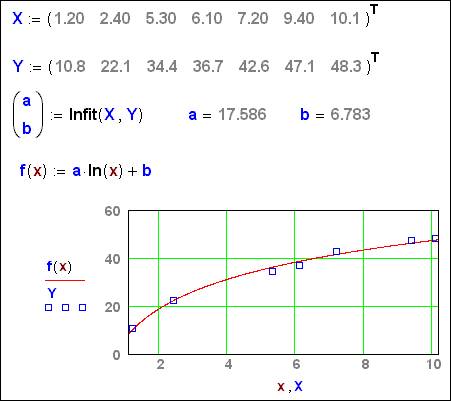
Fig. 7. Call new function lifit
It is possible to think up very much “Smoothing
functions”. The author cannot remember, what from them are built-in in Mathcad,
and what is not present. He acts easier – see fig. 7a, where the mechanism of
approximation by function of any kind with any number of factors is realized.
It is possible to advise to firm MathSoft to not enter new individual functions
of approximation, and to develop and to build in Mathcad the universal tool of
approximation. For example, such, with what is shown in a fig. 7a.

Fig. 7a. Universal method of Smoothing by Minimize