УДК
621.1.36.7 (035.5)
Справочники-решебники
по теплоэнергетике: проблемы и решения
Очков В.Ф.1, 2,
доктор техн. наук, Лоскутова Т.М.1, инж., Чжо Ко Ко1,
студ.
Журнал Теплоэнергетика, №3,
2010 г., С. 65-69
Излагаются
проблемы создания и наполнения сетевых, интерактивных, открытых справочников
для специалистов-теплоэнергетиков. Рассматривается частная проблема — создание
«живых» расчетов с использованием технологии «облачных» вычислений.
1111250,
Москва, Красноказарменная ул., д. 14. МЭИ.
2111250,
Москва, Красноказарменная ул., д. 17, ООО «Триеру».
В
настоящее время бурно развиваются технологии публикации в
Интернете расчетных документов3, созданных
в средах математических программ [1—4]. Такие документы публикуются не только
для просмотра (это делалось и раньше), но и для полноценного расчета по ним.
Они дают возможность изменять исходные данные и получать ответ в численном и
графическом виде, а также все промежуточные результаты расчета с представлением
соответствующих формул и численных значений задействованных в формулах
переменных.
3Это происходит в
рамках общей тенденции развития технологии так называемых “облачных” вычислений
(cloud computing) —
предоставления пользователям компьютеров удаленных вычислительных мощностей и
дискового пространства («облаков»), а также каналов связи. Пользователю не
нужно будет ставить на свой персональный компьютер какие-либо прикладные
программы — все можно будет найти в Интернете за умеренную абонентскую
плату или даже бесплатно.
С
помощью таких сетевых, интерактивных, открытых расчетных документов можно не
только изучать те или иные методы решения конкретных задач (это можно делать и
без компьютера, открыв обычный, напечатанный на бумаге учебник, задачник или
решебник4),
но и добиваться практической цели — производить расчеты и получать новые
ответы при новых исходных данных.
4В
задачнике собраны описания задач и ответов по ним,
которые, как правило, размещаются в конце книги. Решебник дополнен
подробным описанием процесса решения задачи — формулами с подставленными в
них конкретными численными значениями.
Самый
популярный математический пакет для инженерно-технических расчетов и расчетов
учебной направленности — это Mathcad [4]. Так сложилось благодаря низкому порогу
вхождения в эту программную среду, наличию русскоязычной версии и обширной
русскоязычной литературы, а также сайтов поддержки (например, www.mathcad.ru). Кроме того, созданные в среде Mathcad расчеты содержат
формулы, которые по внешнему виду ничем не отличаются от формул в печатных
учебниках, задачниках и решебниках, а написание имен переменных полностью
совпадает с тем, какое закрепилось в той или иной научной дисциплине задолго до
появления компьютеров. Все это способствует максимальной открытости
Mathcad-расчетов. Также после минимальной доработки эти расчеты можно опубликовать
(“оживить”) в локальной или глобальной компьютерной сети по технологии Mathcad Application Server — MAS [4].
Авторы
настоящей статьи в течение последних лет, используя технологию MAS, опубликовали в Интернете большое
количество расчетных документов, связанных в первую очередь с энергетикой (www.vpu.ru/mas).
В этом авторам помогают преподаватели и студенты Московского
энергетического института (www.mpei.ru) и других
учебных заведений. Для студентов такая работа — отличный способ изучить ту
или иную учебную дисциплину и одновременно получить навык в создании (или
проведении) открытых,
интерактивных, сетевых расчетов. Для преподавателей и научных
сотрудников — хорошая это возможность изучить современные информационные
технологии и быстро опубликовать свои наработки в области расчета
теплоэнергетических установок.
Операция «оживления» задачников
и решебников по технологии MAS или по другой подобной IT-технологии позволяет
подвергнуть эти методические и справочные материалы серьезному научному
редактированию и тщательной корректуре. При этом решебник превращается в очень
удобный научно-технический справочник: справочник-решебник.
Необходимо
также отметить следующий момент. Использование калькуляторов и компьютеров привело
к тому, что из расчетов были выдавлены единицы измерения. Пакет Mathcad,
оборудованный инструментарием для работы не просто с числами, а с физическими
величинами (длина, масса, время, давление, мощность и т.д. [1, 4]), намного
упрощает расчеты, осуществляет дополнительный контроль их правильности и
устраняет указанную проблему. С появлением математических пакетов «на плечи»
компьютеров легла дополнительная рутинная работа по пересчету небазовых единиц измерения (час, миллиметр, лошадиная сила
и т.п.) в базовые единицы СИ (секунда, метр, ватт и др.), ведь, хорошо
известно, что часто в научной литературе используются внесистемные и даже
вспомогательные единицы измерения.
Однако
самым важным при “оживлении” методических материалов является аспект, который
рассматривается далее. Решение задач часто сводится к решению систем алгебраических,
дифференциальных, интегро-дифференциальных и прочих уравнений. Составителям
задач для решебников приходится идти на разные допущения, упрощения и другие “хитрости”,
чтобы свести решение задач к последовательному счету по набору несложных
формул. Ищется и приводится, например, точное аналитическое решение какой-либо системы
уравнений. Но чаще помещается упрощенное решение с оговорками и допущениями.
Если при этом не дается и не анализируется сама система исходных уравнений
(математическая модель), а только предлагается набор готовых формул, то студент
не до конца будет понимать суть задачи и методы ее решения. Математические
пакеты, оборудованные мощными численными и аналитическими (символьными) средствами
решения систем уравнений, позволяют по-новому формулировать задачу, обращая при
этом основное внимание на ее постановку в виде системы уравнений (создание
математической модели), а не на конкретные методы ее решения.
Для
примера рассмотрим задачу расчета термического КПД (ηt)
идеальной газотурбинной установки (ГТУ), работающей по термодинамическому циклу
Брайтона [5]. Во всех справочниках и учебниках можно найти формулу для расчета
этой величины:
|
|
|
где
π — степень повышения давления в компрессоре ГТУ (отношение давления
за компрессором к давлению перед компрессором); k
—
показатель адиабаты рабочего тела цикла (отношение изобарной теплоемкости к изохорной).
Во
всех справочниках по термодинамике задача о термическом КПД идеальной ГТУ
решается простейшим способом: задаются значения k
и π и по этой (упрощенной) формуле рассчитывается
требуемое значение ηt. При этом, как
правило, не объясняется, как была получена эта формула, что нужно сделать,
чтобы учесть зависимость показателя адиабаты k
от температуры и давления рабочего тела, как учесть неидеальность
процессов сжатия рабочего тела в компрессоре и его расширения (полезную работу)
в газовой турбине и т.д. На рис. 1 показан иной, открытый подход к решению
данной задачи.
Исходными
данными для расчета КПД ГТУ (рис. 1) являются: давление рабочего тела на входе
в компрессор Р1,
степень повышения давления в компрессоре π, температура рабочего тела на
входе в компрессор Т1 и на входе в
газовую турбину Т3, а также значения
удельных изобарной Cp
и изохорной Cv теплоемкостей рабочего
тела (для идеального воздуха: Ср = ![]() R и Сv =
R и Сv = ![]() R, где R — универсальная газовая
постоянная).
R, где R — универсальная газовая
постоянная).
Для
определения термического КПД ГТУ рассчитываются значения удельной энтальпии
рабочего тела Н во всех четырех
точках цикла посредством нахождения определенного интеграла по температуре от
значения Cp.
Определенный интеграл используется и при вычислении значений удельной энтропии S
во всех точках цикла. Конечно, в расчете, показанном на
рис. 1, интегралы можно
убрать, приняв во внимание, что переменная Cp
является константой и может быть выведена из-под знака интеграла. Но в реальных ГТУ используется реальное рабочее тело, теплоемкость
которого зависит от температуры. Подход к решению задачи о КПД ГТУ, показанной
на
рис. 1, позволяет учесть такую зависимость Cp = f(T).
Кроме того, можно также учесть другую «неидеальность» — рост энтропии рабочего тела при его сжатии
в компрессоре (т.е. не S2
= S1,
а S2
> S1)
и расширении в газовой турбине (не S4
= S3,
а S4
> S3).
Несложно также учесть потери давления в камере сгорания (Р3 ≠ Р2) или в атмосфере (Р4
≠ Р1). Вышеприведенная формула
является “закрытой”, ничего не
дающей ни сфере образования, ни промышленности. Расчет же, показанный на
рис. 1,
“открыт” и для изучения, и для привязки
его к реальным схемам ГТУ. На сайте
http://twt.mpei.ac.ru/TTHB/2/ThermCycleMCS.html выложены открытые интерактивные
расчеты по реальным термодинамическим циклам, используемым в отечественной и
мировой энергетике.
Следует
обратить особое внимание на расчеты термодинамического цикла в точках 2 и 4
(см.
рис. 1), где определение значений температуры осуществляется не по
готовым формулам, а в процессе решения интегрального уравнения блоком Given (дано) — Find (найти) пакета Mathcad.
Технология
MAS позволяет студентам не только считать по готовым формулам, меняя исходные
данные, но и самим вводить в расчет нужные зависимости. Причем не только выбирать
их из предложенного списка, что обычно используется, а вводить в расчет ту
зависимость, которая необходима. На рис. 2 показан пример такой работы — расчет
термического КПД термодинамического цикла Отто в
процессе интерактивного экзамена.
Опрашиваемый,
открыв в Интернете страницу, показанную на
рис. 2, должен ввести в текстовые
окна формулы, по которым рассчитываются те или иные величины в точках 1, 2,
3 и 4 цикла Отто. Если уравнения составлены и
введены правильно (именно это и отображено на
рис. 2; сразу после открытия
данной страницы Интернета текстовые окна были пустыми), то после нажатия
клавиши Recalculate итоговый ответ, найденный по
открытому алгоритму расчета термодинамического цикла, должен совпадать с тем,
какой получен по упрощенной формуле (1). В данном Интернет-тесте по термодинамике при расчете параметров
цикла Отто в точках 2 и 4 приходится
составлять и решать уже не одиночное интегральное уравнение (см. рис. 1 с
расчетом ГТУ), а систему интегроалгебраических
уравнений: уравнение Клапейрона—Менделеева и
уравнение, правая часть которого — это определенный интеграл (int),
по которому вычисляется энтропия рабочего тела в конкретной точке.
Два первых автора
данной статьи со своими студентами (один из них является третьим автором) взялись
за труд перевести некоторые задачники и решебники (связанные в первую очередь с
энергетикой) в сетевой, интерактивный, открытый формат. В процессе
такой работы выявляется множество опечаток и ошибок и не только классических, но
и таких, как недостаточность информации (нет объяснения всех переменных и
констант, записанных в формуле, например). Математические пакеты в этом случае прерывают
счет сообщениями об ошибке или выдают ответ, не совпадающий с приведенным в книгах.
К особому типу
решебников можно отнести различного рода нормативные документы (строительные
нормы и правила — СНиПы, например), в которых также
много формул и которые можно и нужно «оживлять» в Интернете. Так, на сайте
http://twt.mpei.ac.ru/MCS/Worksheets/Thermal/Izol-Trub-Teploset.xmcd читатель
может увидеть пример одного из таких «живых» нормативных документов — СНиП по расчету толщины теплоизоляции теплосети.
Недостаточная толщина изоляции приводит к недопустимым тепловым потерям, а
избыточная — к перерасходу теплоизоляционного материала. Эту типичную
технико-экономическую задачу (минимизация общей стоимости проектирования,
сооружения, эксплуатации и последующей утилизации промышленного объекта при
полном выполнении им своих функций) можно каждый раз решать индивидуально, а
можно воспользоваться обобщенными СНиПами,
что в конечном итоге приведет к удешевлению проектирования.
Затрагивая тему
нормативных документов, нельзя не коснуться проблемы сертификации расчетов.
Достоверность информации в «бумажных» справочниках в какой-то мере
подтверждается солидностью соответствующих издательств с их штатом научных
консультантов, редакторов и корректоров. Страницы же Интернета, как правило,
отданы на откуп случайным создателям и не подвергаются жесткому редактированию
и тщательной корректуре. В то же время, и в справочниках весьма солидных
издательств встречается большое число опечаток.
Сертификацию
расчетных документов, опубликованных в Сети, можно проводить двумя способами.
Во-первых, можно пометить в Сети письмо авторитетной организации с подтверждением
правильности расчетов. Во-вторых, можно из сайтов таких организаций делать
ссылки на соответствующие расчетные сайты и упоминать об этом на самом
расчетном сайте.
Справочники-решебники, открытые
в Интернете на сайте МЭИ (ТУ) для интерактивного использовании:
•
по
высшей математике http://twt.mpei.ac.ru/math;
•
по
физическим величинам http://twt.mpei.ac.ru/pvhb;
•
по
теплотехнике и теплоэнергетике http://twt.mpei.ac.ru/tthb;
•
по
основам гидравлики, теплотехники и аэродинамики http://twt.mpei.ac.ru/GDHB/OGTA.html;
•
по
теплофизическим свойствам рабочих тел энергетики http://twt.mpei.ac.ru/ochkov/WSPHB/index.html;
•
по
термодинамическим циклам http://twt.mpei.ac.ru/TTHB/2/ThermCycleMCS.html;
·
по
гидрогазодинамике http://twt.mpei.ac.ru/gdhb;
·
по
трубопроводам ТЭС http://twtmas.mpei.ac.ru/mas/Worksheets/HBPipePP;
·
по
химической кинетике http://twtmas.mpei.ac.ru/mas/Worksheets/Chem/ChimKin.html;
·
по
химической термодинамике http://twt.mpei.ac.ru/TTHB/1/HBThermValues.html;
·
по
электробезопасности http://twt.mpei.ac.ru/TTHB/EB;
·
по
тепломассообмену http://twt.mpei.ac.ru/ochkov/Diff_MC/web_HMT/index_HMT_E-Book.htm;
·
по
ионообменным смолам http://twt.mpei.ac.ru/TTHB/1/Dow;
·
по
теории автоматического регулирования http://twtmas.mpei.ac.ru/mas/Worksheets/Rotach;
·
по
снижению шума от энергетического оборудования http://twt.mpei.ac.ru/TTHB/1/Tupov.html
и др.
Таким образом «оживление»
учебников, задачников и решебников в Интернете позволяет:
· провести ревизию
правильности постановки и решения задач в печатных учебниках и задачниках;
· поместить в Интернете
задачи практической направленности;
· организовать контроль
знаний посредством решения задач не через вычисления, а непосредственно через ввод
формул.
Список литературы5
1. Очков В.Ф. Физические и
экономические величины в Mathcad и Maple (Серия
«Диалог с компьютером»). М.: Финансы и статистика, 2002. –192 с.
2. Очков В.Ф., Яньков Г.Г. Комплекс "справочник+сайт
интернета" и проблема передачи знаний // Труды Академэнерго,
№ 1, 2009 С. 35-43
3. Очков В.Ф. MA и MAS: проблемы
и решения при создании Web-ресурсов
сферы образования // Вопросы Интернет-образования.
2005. № 29. С. 29-32
4. Очков В.Ф. Mathcad 14 для
студентов и инженеров: русская официальная версия. Издательство BHV-Петербург,
2009. – 512 с.
6.
Интернет-расчеты
термодинамических циклов / В.Ф. Очков, А.А. Александров, В.А. Волощук и др. //
Теплоэнергетика. 2009. № 1. С. 77—80.
5Литература, где одним из
авторов является В.Ф.Очков, открыта на сайте
http://twt.mpei.ru/ochkov/work2.htm. Там же можно найти расширенный вариант
данной статьи со всеми работающими Интернет-ссылками.
Рисунки
Рис.
1. Открытый интерактивный сетевой расчет КПД ГТУ
Рис.
2. Сетевой интерактивный экзамен по термодинамике
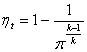 ,
,
