Cloud computing processes and cycles of heat power plants
Ochkov V.F., Alexandrov A., Orlov K., Voloschuk V., Ochkov A.
MPEI (TU) ‑ LLC Trieru - National university of water management and nature resources
Recently publications were made concerning the Internet sites for the calculation of thermophysical properties of water, steam, gases, gas mixtures and materials used in power engineering and other industries (see at http://twt.mpei.ac.ru/ochkov/WSPHB) and the sites for calculation and graphing of diagrams and cycles of heat and power plants (see at http://twt.mpei.ac.ru/TTHB/2/ThermCycleMCS.html). The readers of the magazines or the site surfers bring up the questions: how to work with calculations and how to avoid typical errors. This article is aimed at answering these questions.
First, let us consider the possible methods of work with the site pages.
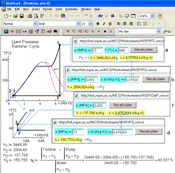
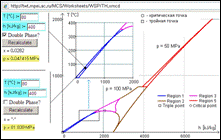
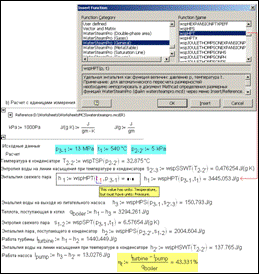
Figure 1 shows the solution of the classical thermodynamic problem: defining thermal efficiency of the Rankine cycle at superheated steam[1] if the parameters of steam (13 MPa[2], 540°Ñ) and pressure in a condenser(5 kPa) are given.
Figure 1. Step-by-step calculation of a Rankine cycle in Mathcad (http://twt.mpei.ac.ru/MCS/Worksheets/WSP/PT.xmcd, PS.xmcd è SatP.xmcd)
The problem is solved online with the engineering calculator Mathcad [6]. As can be seen, there are three WaterSteamPro pages opened in the worksheet.
The page that has address WSP/PT[3] (see the box a in Fig. 1) enables us to define thermophysical properties of water and steam[4] as a function of pressure (p) and temperature (T[5]). Pressure and temperature is a traditional pair of initial values set up in all published tables for one-phase regions for water and steam [for example, 7,8]. As distinct from these handbooks the Internet page WSP/PT enables us to define parameters of water and steam at any value of pressure and temperature, not only at the pre-defined, discrete steps[6].
The site WaterSteamPro is filled with pages that contain different combinations of initial data. In particular, the page WSP/PS (see box b in Figure 1) enables us to calculate thermophysical properties of water and steam as a function of pressure (p) and specific entropy (s – an inverse problem[7] to formulation IAPWS-IF97). This page calculates enthalpy of moist steam at the end of expansion process in a turbine (point 2 in the T –s diagram shown in Figure 1). The process is assumed to be irreversible(s = const) – the value of specific entropy is copied from a-box to the b-box. The point 2’ is water at the saturation line at the condenser pressure. The site page WSP/SatP (box c in Figure 1) helps us to solve this auxiliary problem – to calculate water and steam parameters at the saturation line as a function of pressure[8]. Another call to the page WSP/PS (box d in Figure 1) helps us to define feed pump-exit enthalpy of water (point 3 in T –s diagram). Still, compression process in the pump is considered to be irreversible, constant value of specific entropy is defined in the box c (see Figure 1). After these calls to the site, one has obtained values for the specific enthalpy of water and steam at all four points of the Rankine cycle and can calculate its thermal efficiency, see the bottom part of Figure 1.
The problem shown in Figure 1 is the simplest among those posed to engineers in the heat/ power industry. Although, it is clear, that one can use WaterSteamPro pages to solve complicated problems in any application. As shown in Figure 1, they would supply an engineer with the required data and it is needless to install special software for calculation of water and steam properties. The only thing that is required – to have access to the Internet.
What mistakes could be made in work with pages of WaterSteamPro?
First, a surfer might enter a comma instead of a point as a decimal symbol. The developers of the site (the authors of this article) were going to provide the ability of using a comma together with a point. But it is desirable to follow the world standards and to avoid using the comma as a decimal symbol. There is a difficulty here: all home “paper” monographs, handbooks, guidebooks, articles, published and being prepared for publication continue to use a comma but not a point in decimal numbers. And this tradition is hard to abolish[9]. Another standard imposed by computers is connected with exponent form of a number. Here one should use Roman letter “E”, lowercase or capital, not Cyrillic. For example, if it is required to enter a value of 5 kPa into a box marked with MPa[10], one can type 0.005 (see box b in Figure 1) or 5E-3 (5e-3).
The second mistake, common for the Internet and the “paper” tables, is that a viewer can read the result wrong, alter the number in transfer from the site page into the other application or into the paper sheet. The point is that the numbers given by WaterSteamPro are not texts, divided to separate signs (digits), but pictures, which could be copied into the other document[11]. One can read them using special programs, for example FineReader, or copy them: watching the result in one window and typing it in the other place (in the other box of the Internet page, for example, boxes a and b in Figure 1 in which specific entropy is transferred as a source datum to the box of another page).
“Accurate[12] and complete” reading of the result is possible after installation of the WaterSteamPro package into a user’s computer, which we discuss below.
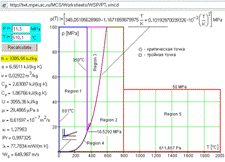
The third mistake can be made when a surfer falls outside the limits of an acceptable region. In this case, as with entering comma, the result would not be represented. Thus we may not consider it as a mistake. The main thing here is to understand what kind of mistake was made. For this reason the site contains links to the figures representing the regions of IAPWS-IF97 formulation. For the pair of initial data pressure-temperature these regions fall on two rectangular areas – see Figure 2. The other combinations of initial data form more complicated configurations.
Figure 2. Calculation of water and steam properties as a function of pressure and temperature (http://twt.mpei.ac.ru/MCS/Worksheets/WSP/PT.xmcd)
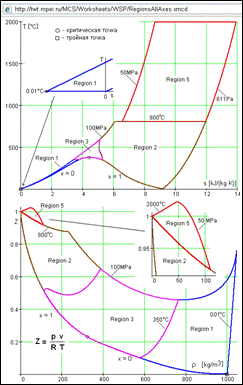
The site page WSP/RegionAllAxes enables us to represent regions of IAPWS-IF97 formulation in various co-ordinates: temperature -entropy (the first diagram in Figure 3), compression index[13] –density (the second diagram), etc. At that, a surfer has the possibility to enlarge any regions, which is also shown in Figure 3 (see regions near the triple point in T –s diagram and in Z –p diagram at high temperatures.
Figure 3. Region boundaries of IAPWS-IF97 formulation in unusual diagrams (http://twt.mpei.ac.ru/MCS/Worksheets/WSP/RegionsAllAxes.xmcd)
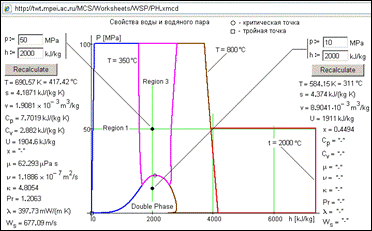
Figure 4 shows that calling page WSP/ÐÍ one can calculate properties of water and steam as functions of pressure (p) and specific enthalpy (h). This combination of initial data shows region of moist vapour, which is possible to access at proper values of p and h: the calculation in one-phase region is shown on the left of p –h diagram (dryness factor õ = ″-″) and two-phase condition – on the right (moist steam, where the x value changes from 0 to 1). In the second case (moist steam) the results are T, s, v, and u. The other properties, ñp, cv, μ, ν, κ, Pr, λ, and Ws are not represented because they are beyond the scope of the posed problem. The similar algorithm is used in the network calculation where initial data are pressure and specific entropy (see box b in Figure 1).
Figure 4. Calculation of water and steam properties as a function of pressure and enthalpy (http://twt.mpei.ac.ru/MCS/Worksheets/WSP/PH.xmcd )
Figure 5 shows more sophisticated combination of initial data: temperature and specific enthalpy.
Figure 5. Calculation of water and steam properties as a function of temperature and enthalpy
(http://twt.mpei.ac.ru/MCS/Worksheets/WSP/TH.xmcd)
Some initial data, for example, T = 80°C and h = 400 kJ/kg, give two possible results. There can be moist steam at ð = 0.047 ÌÐà and water in one-phase region (ð = 81.839 ÌÐà) at these parameters. Additional tick “Double Phase” helps us to avoid this dualism. Thus, we can choose: to make calculation in the two-phase region, where pressure and temperature are connected with each other, or in one-phase region, where the inverse problem is solved by the method if successive approximation – defining pressure as a function of temperature and specific enthalpy.
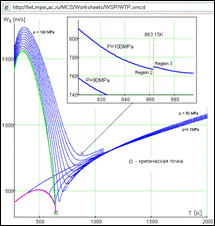
Figures 2, 3, 4, and 5 show not only limits of accessible values for initial data in calculations of water and steam properties[14] but also regions of IAPWS-IF97 formulation: region 1 – water, region 2 –superheated steam, region 3 –near-critical, region 4 –the saturation line, region 5 – steam at high temperature. Such separation is made to optimize working out IAPWS-IF97[15] formulas. A surfer should bear in mind that different formulas are used in different regions and discrepancies can occur on the boundaries. Thus, Figure 6 shows the page WSP/WTP that calculates sound velocity in water and steam as functions of p and T and represents results in a set of isobars. The diagram shows the step between regions 2 and 3 that we should take into consideration while making calculations.
Figure 6. Sound velocity in water and steam (set of isobars http://twt.mpei.ac.ru/MCS/Worksheets/WSP/WTP.xmcd)
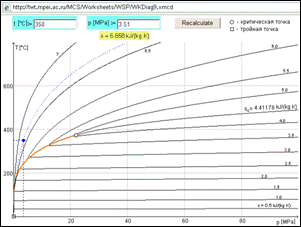
WaterSteamPro site contains pages in which calculation of water and steam properties are visualized by different plots, as shown in Figure 6. Figure 7 shows the similar page WSP/WKDiag9[16] with calculation of specific entropy that represents the point in a set of isentropes in the p –T diagram.
Figure 7. Set of curves s = const in T-p diagram (http://twt.mpei.ac.ru/MCS/Worksheets/WSP/WKDiag9.xmcd)
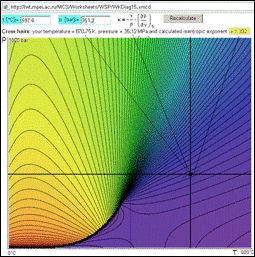
The page WSP/WKDiag15 calculates the isentrope index of water and steam as a function of temperature and pressure. The result is visualized not as values placed in the plot but by the same colour used for the lines (regions) of one level: warm colours show largeness and cold colours ‑ small quantities.
Figure 8. Colored graph of one-level lines at dependence of pressure and temperature on isentrope index (http://twt.mpei.ac.ru/MCS/Worksheets/WSP/WKDiag15.xmcd)
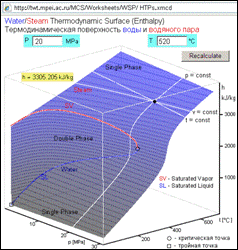
Figure 9 shows calling the site page WSP/ÍÒÐs that calculates specific enthalpy of water or steam and draws the point on the surface h(p, T). The point lies on the isobar, isotherm, and isochor.
Figure 9. Thermodynamic surface of water and steam (h-p-T - http://twt.mpei.ac.ru/MCS/Worksheets/WSP/HTPs.xmcd)
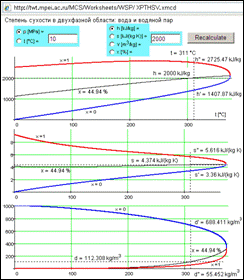
The Internet page WSP/XPTHSV, shown in Figure 10, enables us to calculate parameters of moist vapour (see box b in the Figure 1) one more time. In this case, a viewer has an extended set of input data (p or T; h, s, v or õ), and also a plot of the result, isolines õ = ñonst drawn between boundary curves.
Figure 10 Calculation of moist vapour properties (http://twt.mpei.ac.ru/MCS/Worksheets/WSP/XPTHSV.xmcd)
Visualization of the numerical result allows us, on the one hand, to control whether the values are within the accessible limits and thus to avoid mistakes. And, on the other hand, to see the dynamics of the process, changing the result with altering the initial data. Although, plots make the page voluminous, and enlarge the traffic. For this reason, the “light-weight” Internet pages were created, WSP/ÐÒ, WSP/ÐÍ, WSP/PS, WSP/TH, etc, see above. Moreover, if a user needs only certain parameters of water and steam, for example, enthalpy, he can address to pages WSP/HTP-SI (WSP/HPS-SI and others that calculate corresponding parameters in terms of unit system SI), or WSP/HTP-US (WSP/HTP-US and others in terms of US customary units).
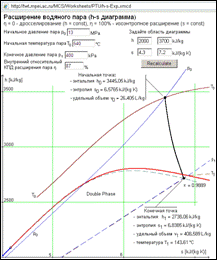
WaterSteamPro contains the sites that calculate not only certain points, as shown in Figures 1, 2, 4, 5 and 7-10 but also the sites that calculates processes, sets of points through which interpolating lines are drawn. Figure 11 shows the site page PTU/h-s-Exp that calculates the expansion process of steam and represents it in the h-s diagram.
Figure 11. h-s diagram of steam expansion (http://twt.mpei.ac.ru/MCS/Worksheets/PTU/h-s-Exp.xmcd)
Figure 1 shows the reversible process of steam expansion in turbine (s=const). Figure 11 shows that a viewer can vary η, efficiency ratio, in the range from 0% (steam throttling at h=const) to 100% (reversible process of steam expansion at s=const) and get corresponding expansion lines in defined region of h-s diagram. Isobars and isotherms are drawn in the initial and the end points of the expansion process. The corresponding site pages were created to represent expansion of steam as other diagrams: T–s diagram (PTU/T-s-Exp), p–s diagram (PTU/p-s-Exp), and p–h diagram (PTU/p-h-Exp).
As was noted in a previous article [1], work with an application on the Internet has its advantages and limitations. The main disadvantage of the network technology is well-known. When it is needed to make a calculation, the connection between a server and a workstation may get discontinued or timed-out. Moreover, many computers have no connection to the Internet and the users get access from the other ones or from special workstations in their offices.
For these reasons the authors provide alternative access to the properties of water and steam. A surfer can download files from the Internet or from distributed CD-ROM, if the network is not accessible.
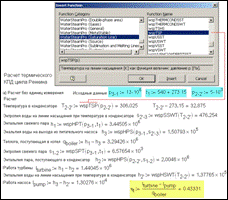
Installing the package WaterSteamPro enables a user to perform calculations described above and also to plug in functions for properties of water, steam, and gas mixtures into widespread applications and programming languages such as Fortran, Pascal, BASIC, C, table processor Excel, and the mathematical package Mathcad (Figure 1).
Figure 12 shows us a Rankine cycle again for the superheated steam (see Figure 1) developed in a Mathcad application with inserted WaterSteamPro functions. At that, all the values are displayed by default in terms of base units of SI system (Pa for pressure, K for temperature, J/kg for specific enthalpy). That is not convenient for those who are accustomed to working with megapascal, bar, atmosphere, centigrade, kilojoule per kilogram, etc.
Figure 12. Calculation of a Rankine cycle in Mathcad using WaterSteamPro functions without dimensions
Moreover, the calculation shown in Figure 12 has no unit control, which can lead to errors. If one clicks the reference to watersteampro.mcd the unit control would work in full force (Figure 13). In particular, it checks if a physical value corresponds with its place as an argument of a WaterSteamPro function (see Figure 13 where we tried to calculate enthalpy of working steam and change positions of the arguments). Also, the numerical value can be displayed in required terms: °Ñ instead of Ê, ÌÐà instead of Ðà, kJ/kg instead of J/kg, etc.
Figure 13. Calculation of a Rankine cycle in Mathcad using WaterSteamPro functions using dimensions
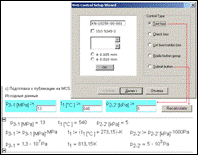
If one wants to publish the calculation shown in Figure 13 on the Internet by Mathcad Calculation Server technology [6] it is sufficient to change the definition symbol (:=) into Text box, Check box, and other web controls. It is also required to insert the “Calculate” button (Submit button – see Figure 14). Click on this button to signal the server that the data have been input.
Figure 14. Publication of a Rankine cycle calculation on the Internet
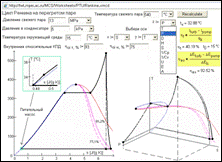
Figure 15. Rankine cycle at superheated steam and plotting of the diagrams (http://twt.mpei.ac.ru/MCS/Worksheets/PTU/Rankine.xmcd)
Figure 15 shows another calculation of a Rankine cycle for superheated steam that differs from those shown in Figures 1, 12, and 13 in the following:
-
It performs not only thermal but also exergy analysis of the cycles. Additionally, it calculates exergy efficiency ηåõ that is less than 100% not “due to the fault of nature” but “through the fault of man”. If the temperature in a condenser had been not 32.88°Ñ but had amounted to 15°Ñ (ambient temperature), exergy efficiency ηåõ would have equaled to 100%
-
Turbine and feed pump losses are taken into consideration in efficiency ratio of steam expansion (see Figure 11, too)
-
A site surfer can choose co-ordinate axes and plot not only conventional diagrams (h-s and T-s) but also custom, even exotic graphs, for example cp-cv, or exergy-anergia.
-
It is possible to draw three-dimensional plots. In particular, Figure 15 shows T-s-p graph that clearly visualizes compression process in a feed pump. On the flat plot it is necessary to zoom this point (more accurately, two points) – see Figure 15 on the left. It is needless to do it in the 3D plot because the points corresponding to the inlet and outlet of the feed pump are divided by additional axis, pressure.
The detailed description of the calculation shown in Figure 15 is given at http://twt.mpei.ac.ru/TTHB/2/ThermCycleMCS-Create.html.
As was noted above, the site page shown in Figure 15 enables us to plot various graphs – conventional, unusual, even exotic ones. Heat engineers have not one opinion which of diagrams are considered as conventional. Surely, h-s and T-s diagrams are set up in all guide books. Although, all good things come in threes. What diagram can be settled as the third traditional? Many a one put forward pressure p, more accurately, log P-s diagram. Although, Figure 16 shows, this is not the case.
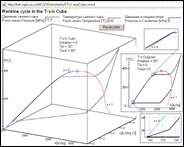
Figure 16. Rankine cycle “within a cube” (T-s, h-s, and T-h diagrams - http://twt.mpei.ac.ru/MCS/Worksheets/WSP/wspCube.xmcd)
Figure 16 shows a virtual object that could be called Rankine cube. It contains three dimensional T-s-h diagram of a cycle. When a viewer turns it to one side he would see h-s diagram, on the second side there would be T-s diagram, on the third side – T-h diagram that seems to be considered as the third conventional one. What is most notable about this diagram is that its compression line covers the region of moist vapour (see right bottom corner in Figure 16) and the line of water heating in a boiler intercross the saturation line. But it is easy to find out that these cover and crossing are false if we turn into three dimensional plot and add one more axis, “pressure”. Besides, we can return to the example shown in Figure 5 in which the same point at T-s diagram has different pressure
Conclusion
WaterSteamPro package, calculating pages of WaterSteamPro sites and Thermal Cycles are useful for those who need to compute properties of working media and heat carriers in power engineering, to make online calculations, to visualize processes and cycles in heat and power plants.
Development of online calculations for thermal engineering is a part of the innovative educational program (http://inedu.mpei.ru) performed by Moscow Power Engineering Institute (www.mpei.ru) within the bounds of development of “Electronic Encyclopedia of Power Engineering” (www.trie.ru).
References
-
Î÷êîâ Â.Ô., Àëåêñàíäðîâ À.À, Îðëîâ Ê.À., Î÷êîâ À.Â. Ñâîéñòâà òåïëîíîñèòåëåé è ðàáî÷èõ òåë ýíåðãåòèêè: èíôîðìàöèÿ â èíòåðíåòå. // Íîâîå â ðîññèéñêîé ýëåêòðîýíåðãåòèêå. ¹1. 2008 (http://twt.mpei.ac.ru/ochkov/WSPHB/NREE-1-2008/index.html)
-
Àëåêñàíäðîâ À.À., Îðëîâ Ê.À., Î÷êîâ Â.Ô. Ìàòåìàòè÷åñêèå ïàêåòû – íîâûå ïîäõîäû ïðè ðàñ÷åòàõ ïðîöåññîâ òåðìîäèíàìèêè è äðóãèõ íàó÷íûõ äèñöèïëèí // Èçâåñòèÿ âûñøèõ ó÷åáíûõ çàâåäåíèé. Ïðîáëåìû ýíåðãåòèêè. – 2005 (http://twt.mpei.ac.ru/ochkov/Mat_h_Therm/index.html)
-
OCHKOV Valeriy, ALEXANDROV Alexey, ORLOV Konstantin, OCHKOV Alexey. Thermodynamic Cycles: Calculations on the Internet // Proceedings of the 7-th Conference «Power System Engineering, Thermodynamics & Fluid Flow», June 26-27, 2008, Pilsen, Czech Republic
-
Àëåêñàíäðîâ À.À., Î÷êîâ Â.Ô., Îðëîâ Ê.À., Î÷êîâ À.Â. Òåïëîôèçè÷åñêèå ñâîéñòâà âîäû è âîäÿíîãî ïàðà â Èíòåðíåòå // Ïðîìûøëåííàÿ ýíåðãåòèêà ¹ 2, 2007 (http://twt.mpei.ac.ru/ochkov/WspIn/index.html)
-
Î÷êîâ Â.Ô., Àëåêñàíäðîâ À.À., Îðëîâ Ê.À. Òåðìîäèíàìè÷åñêèå öèêëû: ðàñ÷åòû â Èíòåðíåòå // Âåñòíèê ÌÝÈ ¹ 1, 2007
-
Î÷êîâ Â.Ô. Mathcad 14 äëÿ ñòóäåíòîâ, èíæåíåðîâ êîíñòðóêòîðîâ. – Ñ-Ïåòåðáóðã: ÁÕÂ-Ïåòåðáóðã, 2007 (http://twt.mpei.ac.ru/ochkov/Mathcad_14/index.html)
-
Àëåêñàíäðîâ À.À., Ãðèãîðüåâ Á.À. Òàáëèöû òåðìîäèíàìè÷åñêèõ ñâîéñòâ âîäû è âîäÿíîãî ïàðà. – Ì.: Èçä. ÌÝÈ, 1999
-
W.Wagner, H.-J. Kretzschmar. International Steam Tables – Properties of Water and Steam based on the Industrial Formulation IAPWS-IF97. // Springer, 2008 (http://www.springer.com/engineering/mechanical+eng/book/978-3-540-21419-9)
-
Î÷êîâ Â.Ô. Ôèçè÷åñêèå è ýêîíîìè÷åñêèå âåëè÷èíû â Mathcad è Maple. Ì.: Ôèíàíñû è ñòàòèñòèêà, 2002 (http://twt.mpei.ac.ru/ochkov/Units/Forword_book.htm)