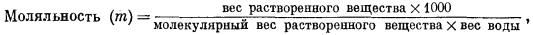
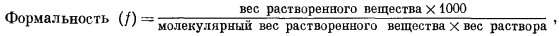
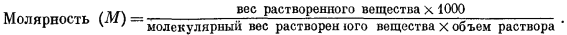
| Р.М. Гаррелс, Ч.Л. Крайст | Растворы, минералы, равновесия |
|
|
|
|
|
|
Настоящая книга посвящена в основном одной простой теме — как одновременно изобразить несколько различных химических реакций. Учитывая важность, которая всегда придается анализу минеральных ассоциаций, представляется по меньшей мере странным, что при графическом изображении равновесных соотношений между минералами используется весьма ограниченное количество методов. Обычно в работах фигурируют такие диаграммы, которые либо выражают зависимость соотношений устойчивости минералов от температуры и давления (эти диаграммы строятся в прямоугольной системе координат), либо характеризуют состав при постоянных температуре и давлении (тогда применяются треугольные и тетраэдрические графики). Кроме того, существуют многочисленные способы комбинации простых диаграмм, например на треугольники состава могут накладываться изотермы или изобары.
Ценность подобных графических построений велика хотя бы потому, что они очень часто применяются на практике. Однако сколько-нибудь полное описание этих способов изображения химических соотношений заняло бы слишком много места. Поскольку всегда можно найти учебники, где излагаются принципы составления и интерпретация таких диаграмм, в настоящей книге они будут рассмотрены только в самом общем виде и в связи с другими типами диаграмм. Поэтому настоящая книга может показаться односторонней тому читателю, который хотел бы ознакомиться со всеми существующими методами графического анализа химических соотношений. Действительно, цель ее заключается прежде всего в том, чтобы вооружить геологов серией очень нужных им диаграмм совершенно иного типа.
Все способы графического изображения прежде всего должны быть основаны на расчете отдельных химических реакции. Указанное положение, казалось бы, совершенно очевидно. Однако для изображения полей устойчивости стремятся прежде всего использовать диаграммы давление — температура — состав и часто забывают о существовании методов расчета соотношений устойчивости. Если вернуться к частным уравнениям и рассматривать их как отдельные «строительные блоки», то хорошо выявляются многочисленные способы составления графиков, с помощью которых можно показать взаимоотношения между отдельными уравнениями. Выбор способа изображения будет зависеть от поставленной задачи.
Поскольку химическая терминология стала весьма сложной и в ней применяются различные системы условных обозначений, представляется целесообразным, прежде чем перейти даже к простейшим химическим уравнениям, посвятить специальный раздел определению терминов и символов.
В настоящей работе принят обычный способ написания формул (H2O CO2 и т. д.). Стехиометрические коэффициенты, как правило, выражаются целыми числами, обозначающими только атомные отношения элементов. В ряде случаев, там, где необходимо отразить структуру соединений, могут быть использованы большие кратные числа. Например, при написании формулы в виде Н4SiO4 имеется в виду только то обстоятельство, что отношение атомов Н, Si и О в соединении равно 4 : 1 : 4, но вопрос, не обладает ли данная молекула составом H8Si2O8 или H16Si4016, остается открытым. Если же формула написана с большими кратными числами, как, например, V303-9, то это означает, что приняты во внимание структурные данные.
Чтобы указать на имеющуюся полимеризацию, степень которой неизвестна, формула с минимальными стехиометрическими коэффициентами заключается в скобки и ставится индекс х, например (Н4SiO4)x. Для обозначений атомных соотношений в соединениях переменного состава используются дробные индексы в части формулы, заключенной в скобки. Так, формула кальцита с определенным содержанием магния будет иметь вид (Ca0,9Mg0,1)C03.
Ниже приводится список сокращений, которые помещаются после формул и указывают на фазовое состояние соответствующего вещества или содержат какие-либо иные дополнительные сведения.
| aморфн | . . . . . | аморфное |
| n атм | . . . . . | при давлении в n атмосфер |
| стекл | . . . . . | стекловатое |
| крист | . . . . . | кристаллическое |
| Т | . . . . . | температура в градусах по шкале Кельвина |
| жидк | . . . . . | жидкое |
| газ | . . . . . | газообразное |
| водн | . . . . . | в водном растворе |
| t | . . . . . | температура в градусах по шкале Цельсия |
По мере необходимости даются дополнительные примечания, указывающие на полиморфную модификацию кристаллического вещества.
Перевод градусов Цельсия в градусы абсолютной шкалы Кельвина производится согласно равенству 0° С = 273,150° К. Таким образом, t = 25° С равнозначно Т = 298,15° К. Если в индексе температура дается в градусах Цельсия, то в этом случае рядом с числовым значением ставится знак С.
Так, например, если написано O2 газ 298,15° 1 атм, то имеется в виду молекулярный газообразный кислород при 298,15° К и 1 атм давления;
данному выражению эквивалентно другое - О2 газ 25° С 1 атмЧSромбич означает кристаллическую ромбическую серу. Чаще всего в тексте будут встречаться условные обозначения, перечисленные выше; случаи использования каких-либо иных обозначений будут оговорены особо.
Полный перечень терминов и их символов наряду с физическими константами, принятыми в данной книге, приведен в приложении 1.
Поскольку многие природные растворы почти нацело состоят из воды, для них удобнее использовать такие единицы концентрации, как моляльность и молярность, которые употребляются химиками специально для сильно разбавленных водных растворов. Можно пользоваться и мольными долями, ибо эта единица концентрации, по-видимому, наиболее подходяща для растворов всех типов.
Моляльность m выражается числом молей растворенного вещества в 1000 г воды; формальность1 f представляет собой число молей в 1000 г раствора, а молярностъ М определяется числом молей растворенного вещества в 1000 мл раствора. В последующих расчетах наиболее часто будет использоваться моляльность. Для разбавленных водных растворов разница между m, f и М столь ничтожна, что во многих случаях ею можно пренебречь. Например, при подсчетах изменения свободной энергии расхождение в результатах, возникающее за счет этой разницы, меньше, чем ошибки в определении самих величин свободной энергии.
Различия и соотношения между тремя перечисленными единицами концентрации определяются следующими выражениями (вес дан в граммах, объем - в миллилитрах):
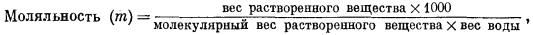 |
(1.1) |
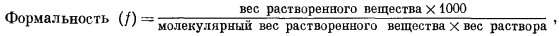 |
(1.2) |
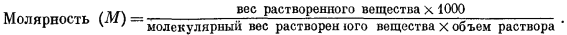 |
(1.3) |
Разделив выражение (1.1) на выражение (1.2), получим
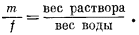 |
(1.4) |
Поскольку
вес воды = вес раствора — суммарный вес растворенных веществ,
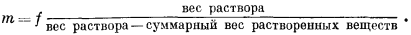 |
(1.5) |
Разделив уравнение (1.3) на уравнение (1.2), получим
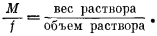 |
(1.6) |
Поскольку
| M = f ґ плотность раствора. | (1.7) |
Из уравнений (1.4) и (1.7) следует
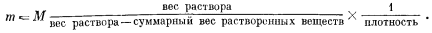 |
(1.8) |
В качестве примера использования перечисленных выще соотношений приведем расчет формальности, моляльности и молярности иона натрия в соляном растворе плотностью 1,008 г/см3. Сумма растворенных твердых веществ в таком растворе составляет 10000 ч. на млн., причем на долю ионов натрия приходится 1000 ч. на млн. Поскольку в анализе дано отношение веса растворенных веществ к весу раствора, то сначала определим формальность, пользуясь уравнением (1.2):

Затем из уравнения (1.5) определим
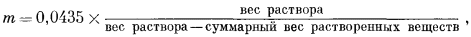
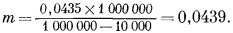
Согласно уравнению (1.7),
M = f ґ плотность раствора = 0,0435 ґ 1,008 = 0,0438
Следовательно, для данного соляного раствора, достаточно характерного для природных подземных вод, f = 0,0435, m = 0,0439 и М = 0,0438. Расхождения в величинах формальности, моляльности и молярности возрастают пропорционально увеличению суммарного веса растворенных веществ. Однако при той степени разбавления, которая свойственна природным водам, это расхождение настолько мало, что им можно пренебречь.
Мольная доля данного компонента в каком-либо растворе (жидком, твердом или газовом) определяется как отношение числа молей данного компонента к суммарному количеству молей всех компонентов.
 |
(1.9) |
При таких расчетах обычно не делают различия между растворенным веществом и растворителем. Так, мольная доля NaCl в 1,0-моляльном растворе составляет
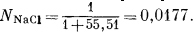
Число 55,51- количество молей воды в 1000 г воды.
Концентрации, выражаемые в виде моляльности, формальности или мольных долей, имеют то преимущество, что их цифровое значение не зависит от температуры и давления. Молярность раствора изменяется с изменением температуры и давления.
В настоящей работе будут использованы почти исключительно такие единицы концентрации, как моляльность, парциальное давление и мольная доля. Моляльность данного компонента обозначается либо буквой m, индекс к которой соответствует химическому символу компонента, например mFe2+, либо при помощи круглых скобок, в которые этот символ заключен (Fe2+). Парциальное давление обозначено буквой Р; в индексе при Р приводится химический символ компонента, например РO2, РCO2. Мольные доли обозначаются буквой N; индекс при N - химический символ данного компонента, например NPbS, NFeO.
В большинстве расчетов, приводимых в данной книге, участвует активность, или термодинамическая концентрация, вещества. Активность характеризует эффективную концентрацию реагента или продукта химической реакции. Огромные усилия исследователей химических реакций затрачены на выявление соотношений между концентрациями реагирующих веществ или продуктов реакций, определяемыми на основании состава системы, и активностями, устанавливаемыми по термодинамическим свойствам этой системы.
Стандартное состояние любого вещества определяется эталонными условиями, причем активность любого чистого вещества в его стандартном состоянии считается равной единице. В зависимости от поставленной задачи выбирается различное стандартное состояние.
За стандартное состояние твердого элемента или соединения обычно принимают чистое вещество при стандартных условиях - 1 атм давления и определенной температуре. Так, активность бывает равной единице и для Sромбич 298,15° и для Fe2О3 гематит 400°. Если величина давления при этом не указывается, то подразумевается, что оно равно 1 атм.
Стандартным состоянием жидкого элемента или соединения считают чистую жидкость при стандартных условиях - 1 атм давления и определенной температуре. Так, чистая жидкая вода при данной температуре и 1 атм общего давления находится в стандартном состоянии и обладает активностью, равной единице. Поскольку обычно выбирают температуру 298,15° К, т. е. 25° С, то такую температуру иногда называют табличной.
Стандартное состояние для газообразного элемента или соединения определяется не так просто, как для твердого вещества или жидкости. За стандартное состояние идеального газа (который удовлетворяет соотношению PV = nRT) принимают рассматриваемый газ при данной температуре и давлении 1 атм. Стандартным состоянием реального газа с активностью, равной единице, считают этот газ при данной температуре и таком давлении, которое соответствовало бы 1 атм, если бы газ вел себя как идеальный.
Стандартное состояние растворенных компонентов, например Fe2+водн или Н4SiO4 водн, определяют, как и для газов, путем экстраполяции до активности, равной единице, исходя из поведения бесконечно разбавленных растворов (в последнем случае поведение растворенного компонента идеально, т. е. его активность и концентрация численно равны). Определения стандартного состояния растворенных веществ и газов мы рассмотрим подробнее в гл. 2.
Активность обозначается буквой а; в индексе при ней приводится химический символ данного компонента, например aFе2+, аFe2О3. Кроме того, на активность будут указывать квадратные скобки, заключающие химический символ компонента [Fe2+], [Fe2О3]. Активность веществ в стандартном состоянии (активность, равная единице) обозначается символом а°. Активность представляет собой безразмерную величину.
Одним из краеугольных камней учения о равновесных соотношениях между минералами является закон действия масс. Уже давно установлено, что направление реакции зависит от концентрации реагирующих веществ и продуктов реакции. Система считается равновесной, если скорости протекания реакции вправо и влево равны. После любого временного нарушения системы, например небольшого изменения температуры или давления, система возвратится в свое первоначальное состояние, если температура и давление станут прежними. В случае равновесной системы соотношение концентраций реагентов и продуктов реакции определяется следующим образом: произведение активностей продуктов реакции, каждая из которых возведена в степень, соответствующую числовому коэффициенту компонента, деленное на произведение активностей реагентов, каждая из которых возведена в соответствующую степень, при данной температуре есть величина постоянная. Эта термодинамическая константа равновесия меняется в зависимости от температуры, но при любой данной температуре она не зависит от общего давления.
К сожалению, этот простой, по сути дела, закон выражается в виде очень громоздких уравнений. Проще говоря, если в результате реакции между b молями вещества В и с молями вещества С наступает равновесие с продуктами реакции, представленными d молями вещества D и е молями вещества Е, т. е. если
bB + cC = dD + eE,
то
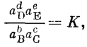 |
(1.10) |
где К - термодинамическая константа равновесия.
Если рассматривать химические реакции с точки зрения изменения энергии, то можно дать новое определение равновесия. Любая система, не находящаяся в равновесии, будет самопроизвольно претерпевать изменение с освобождением энергии. На этом основании равновесное состояние определяется отношением
есвободная энергия продуктов реакции - есвободная энергия реагентов = 0,
если реагенты и продукты реакции находятся при одинаковых температуре и давлении.
Далее нужно выявить соотношение между изменением свободной энергии реакций и константами равновесия тех же реакций, для чего необходимо знать величины свободной энергии различных веществ. При этом достаточно знать лишь величину стандартной свободной энергии образования, т. е. свободную энергию реакции, приводящей к образованию 1 моль веществ в их стандартном состоянии из стабильных элементов, также находившихся при стандартных условиях.
Принято считать, что стандартная свободная энергия образования стабильной модификации элемента в стандартном состоянии равна нулю. Так, например, равна нулю стандартная свободная энергия образования Sромбич 298, 15°. Заметим, что активность Sмонокл 298,15° в стандартном состоянии равна единице, но стандартная свободная энергия образования этого вещества не равна нулю, поскольку оно не отвечает стабильной модификации серы при данной температуре.
Точно так же удобно приравнять нулю стандартную свободную энергию образования водородного иона в водном растворе.
Стандартная свободная энергия образования обозначается символом DF°обр. Температура приводится в качестве дополнительного индекса, например DF°обр T или DF°обр t. Обычно температура дается в градусах Кельвина; если же указана температура в градусах Цельсия, то вводится добавочное обозначение, например DF°обр 298,15° или DF°обр25° C. Величины DF°обр веществ, представляющих интерес для геологов, приведены в приложении 2. Значительно более полный список значений можно найти в работах перечень которых помещен в конце приложения 2.
Стандартная свободная энергия реакции есть сумма свободных энергий образования продуктов реакции в их стандартном состоянии за вычетом суммы свободных энергий образования исходных реагирующих веществ в их стандартном состоянии:
DF°реакции = E DF°обр продуктов реакции - E DF°обр реагентов.
Стандартная свободная энергия реакции связана с константой равновесия следующим равенством:
| DF°реакции = —RT ln K, | (1.11) |
в котором
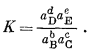
R - (универсальная) газовая постоянная, а Т - абсолютная температура. При 298,15°
DF°реакции(ккал) = —0,001987 ккал/град ґ 298,15° ґ 2,303 lg K,
| DF°реакции = —1,364 lg K. | (1.12) |
Данное соотношение между DF°реакции и константой равновесия представляет собой частный случай соотношения между изменением стандартной свободной энергии реакции и активностями участвующих в реакции веществ для равновесной системы.
В более общем виде, характеризующем любую химическую реакцию,
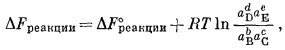 |
(1.13) |
где активности реагентов и продуктов реакции (измеренные при одинаковой температуре) теперь относятся к начальной и конечной активностям веществ, участвующих в данном химическом превращении. Так как в соответствии с первоначальным определением DF°реакции, где аB = аC = aD = aE = 1, считаем, что DFреакции = DF°реакции + RT ln 1, то DFреакции = DF°реакции.
Если для данной реакции DFреакции № 0, то частное
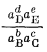
называется квотантом реакции2 Q в отличие от константы равновесия К. Для равновесной системы DFреакции = 0 и DF°реакции = - RТ ln К.
Равновесие достигается лишь в том случае, когда изменение свободной энергии реакции равно нулю. Если в реакции участвуют только чистые твердые вещества при данной температуре и давлении 1 атм, то эти твердые вещества находятся в стандартном состоянии и обладают активностями, равными единице. При таких условиях для реакции
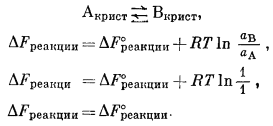
Эти два чистых твердых вещества будут находиться в равновесии, когда DFреакции = DF°реакции = 0. Лишь случайно может оказаться, что при произвольно выбранной температуре е DFобр продуктов реакции будет равно е DFобр реагирующих веществ. Соотношение DFреакции = DF°реакции удобно потому, что благодаря ему реакции между твердыми веществами попадают в категорию "либо идущих - либо неидущих" (go-no-go) 3. Исследуя любую реакцию, можно быстро выяснить, является ли предложенный реагент(ы) или продукт(ы) реакции устойчивым(и) веществом(ами) при данной температуре и атмосферном давлении (в случае если эти твердые вещества находятся в стандартном состоянии). Если DF°реакции отрицательна, т. е. если происходит выделение энергии, то продукт(ы) реакции устойчив(ы) относительно реагента(ов); если же DF°реакции положительна, то устойчив(ы) реагент(ы).
Например, имеются два моноокисла свинца - красная и желтая разновидности. Для такой реакции
PbOкрист красн 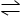 PbOкрист желт (25°С, 1 атм),
PbOкрист желт (25°С, 1 атм),
DF°обр PbOжелт — DF°обр PbOкрасн = DF°реакции,
—45,05 — (—45,25) = +0,20 ккал.
Следовательно, устойчивой оказывается фаза РbOкрасн. Этот метод удобен для определения относительной устойчивости любых полиморфных веществ при стандартных условиях.
В качестве примера реакции, включающей два реагирующих вещества и два продукта реакции, приведем следующую реакцию, представляющую интерес для геологов:
PbCO3 крист + CaSO4 крист 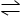 PbSO4 крист + CaCO3 крист кальцит (25°C, 1 атм),
PbSO4 крист + CaCO3 крист кальцит (25°C, 1 атм),
DF°обр PbSO4 + DF°обр CaSO4 = DF°реакции,
(—193,89) + (—269,78) — (—149,7) — (—315,56) = +1,59 ккал.
Таким образом, ассоциация церрусита с ангидритом устойчива, а ассоциация англезита и кальцита неустойчива. Иными словами, если бы природные реакции шли до конца, то ассоциация англезита с кальцитом в стандартных условиях была бы запрещенной. Только изменяя температуру или давление (или и температуру, и давление), все эти четыре вещества можно привести в равновесие.
Для случая реакций только между чистыми твердыми веществами легко определить влияние подобных изменений давления и температуры, переписав общее уравнение изменения свободной энергии:
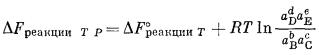 |
(1.14) |
Здесь учитывается тот факт, что величина DF°реакции зависит от температуры и что относительные активности твердых веществ, участвующих в реакции, зависят от общего давления. Следовательно, DFреакции ТР может стремиться к нулю, т. е. система может прийти к равновесию, если температура и давление изменятся таким образом, что окажется справедливым уравнение
DF°реакции T = —RT ln QP.
При точном соблюдении перечисленных соотношений данный процесс в принципе всегда может доходить до конца. Однако для некоторых химических систем создать такие условия практически чрезвычайно трудно.
Реакции, в которых принимают участие только твердые вещества и чистая или почти чистая вода в жидком состоянии, могут рассматриваться как реакции между твердыми веществами, поскольку активность чистой воды также постоянна. Это позволяет исследовать такие соотношения, как устойчивость окислов по отношению к гидроокислам или окислов по отношению к гидратам в сильно разбавленных водных растворах. Например,
Al2O3 Ч H2Oжидк = Al2O3 Ч 3H2Oгиббсит (25°C, 1 атм),
DF°обр гиббсит — DF°обр бемит — 2DF°обр H2O = DF°реакции,
(—554,6) — (—435,0) — (—113,4) = —6,2 ккал.
Таким образом, в разбавленном водном растворе при 25° С и 1 атм общего давления гиббсит по отношению к бёмиту представляет собой устойчивую фазу.
Если в реакции участвует газовая фаза, то в стандартных условиях равновесие всегда может быть достигнуто путем изменения парциального давления4 этого газа. Например, если в реакции принимает участие один газ
FeOкрист + CO2 газ = FeCO3 крист,
то константа равновесия будет равна
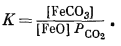
Поскольку активности твердых веществ при 1 атм общего давления равны единице, это выражение упрощается:
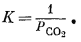
Таким образом, реакция с участием чистых твердых веществ и одного газа при стандартных условиях оказывается равновесной лишь при одном определенном парциальном давлении этого газа. В рассматриваемом случае
DF°обр FeCO3 — DF°обр FeO — DF°обр CO2 = DF°реакции,
(—161,06) — (—58,4) — (—94,26) = —8,40 ккал.
Тогда
—1,364 lg K = —8,40,
lg K = 6,1.
и
PCO2 = 10—6,1 атм.
Это означает, что в условиях земной поверхности соединение FeO по отношению к сидериту неустойчиво, так как парциальное давление СО2 в атмосфере равно примерно 10—3,5 атм. Вместе с тем FeO может быть неустойчиво и по отношению к другим соединениям, поскольку в приведенной реакции исследована только пара FeO — FеСО3. Все же на основании этой частной реакции получен определенный ответ на частный вопрос.
Многие реакции могут быть выражены через значения давлений двух или даже большего количества газов. Константа равновесия при этом определяется таким же путем, как и в случае одного газа:
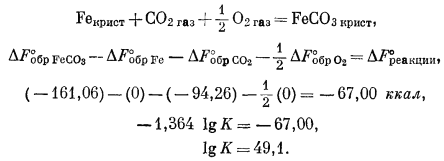
Отсюда
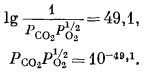
Реакции с участием растворенных компонентов, как и реакции с участием газовой фазы, можно выразить через активности растворенных компонентов. Вероятно, в скором времени в нашем распоряжении окажутся термохимические данные для широкого диапазона температур и давлений, но имеющиеся в настоящее время сведения позволяют рассматривать реакции с участием растворенных компонентов лишь при 298,15° К и 1 атм. Поэтому последующее описание реакций подобного типа будет относиться только к стандартным условиям температуры и давления. Своеобразие этой книги заключается в широком привлечении данных для растворенных компонентов. Трудно понять, чем объясняется слабое использование термохимических данных исследователями, интересующимися геохимическими превращениями в области низких температур и давлений.
Что произойдет, если гематит поместить в воду? Какова активность иона окисного железа? На вопросы подобного рода можно ответить, хотя бы частично, рассмотрев реакцию
Fe2O3 крист + 3H2Oжидк = 2Fe3+водн + 6OH—водн.
Константа равновесия для этой реакции определяется выражением
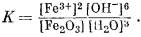
Активности Fe2О3 крист и H2O равны единице, а поэтому
K = [Fe3+]2[OH—]6.
Стандартная свободная энергия реакции равна
2DF°обр Fe3+ + 6DF°обр OH— — DF°обр Fe2O3 — 3DF°обр H2O = DF°реакции,
2 ґ (—2,53) + 6 ґ (—37,6) — (—177,1) - 3 ґ (—56,69) = 116,51 ккал;
тогда
—1,364 lg K = 116,51,
lg K = —85,4 = lg [Fe3+]2 [OH—]6.
После преобразования и упрощения получаем
lg [Fe3+] = —42,7 — 3 lg [OH—].
Следовательно, активность иона окисного железа является функцией активности гидроксила в растворе, возведенной в куб. Устойчивость Fе2О3 в воде можно изобразить графически в виде линейного уравнения, приняв за оси координат lg [Fe3+] и lg [ОН—].
Подобно диаграммам парциального давления, назовем такие графики диаграммами активность - активность. Несомненно, диаграммы активность - активность, у которых за оси приняты активности растворенных компонентов, удобно использовать для изображения соотношений устойчивости. Поскольку во многих реакциях, представляющих интерес для геологов, участвует активность водородных ионов (либо эти реакции можно выразить через активность водородных ионов), особое внимание уделяется такому способу составления уравнений реакций, при котором активность водородных ионов является одной из характеристических переменных.
Роль рН. Активность водородных ионов либо входит в уравнение реакций с участием растворенных компонентов, либо при желании ее можно туда ввести. Поскольку экспериментальные методы позволяют измерить активность водородных ионов, то существует тенденция использовать там, где это возможно, aH+ в качестве характеристической переменной, с тем чтобы при сравнении различных реакций иметь общую контрольную величину активности. Так как в большинстве случаев активности выражаются в виде логарифмических функций, уже давно был предложен термин рН:
| pH = —lg aH+ | (1.15) |
Если мы обратимся к реакции, рассмотренной в предыдущем разделе,
Fe2O3 крист + 3H2Oжидк = 2Fe3+водн + 6OH—водн, то увидим, что ее можно преобразовать, дополнив реакцией диссоциации воды:
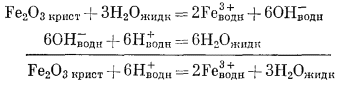
Единственные переменные величины представлены активностями Fе3+водн и H+водн. Константа равновесия равна
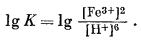
После преобразования получаем
lg K = 2 lg [Fe3+] - 6 lg [H+].
Подставляя
pH = —lg [H+],
находим
lg K = 2 lg [Fe3+] + 6pH.
Число реакций, которые могут быть выражены через рН в качестве переменной величины, весьма велико. Сюда относятся реакции с участием не только окислов, гидроокислов и основных солей, но также реакции с участием карбонатов, силикатов, сульфидов и фосфатов.
Р о л ь Eh. Если для огромного числа реакций в качестве переменной величины можно использовать рН, то окислительный потенциал Eh применим для сравнения условий равновесия между различными веществами. Теперь после определения понятий рН и парциального давления газов нетрудно перейти и к изложению представлений о Eh.
При рассмотрении Eh прежде всего следует разделить окислительно-восстановительные реакции на полуэлементы, или полуреакции. Так, реакцию окисления иона закисного железа в ион окнсного железа можно выразить через взаимодействие с ионом водорода. Уравнение реакции будет иметь следующий вид:
| Fe2+водн + H+водн = Fe3+водн + 1/2 H2 газ. | (1.16) |
Ионы закисного железа окисляются до ионов окисного железа, а водородные ионы восстанавливаются до водорода. Всю эту реакцию можно рассматривать как сумму двух процессов - окисления иона закисного железа до окисного с потерей электрона
| Fe2+водн = Fe3+водн + e | (1.17) |
и восстановления иона H+ до водорода, которое сопровождается приобретением электрона,
| H+водн + e = 1/2 H2 газ. | (1.18) |
Каждая из этих двух реакций называется полуэлементной реакцией или. полуреакцией. Рассмотрим соотношение свободных энергий:
DF°обр
Fe3+ + DF°обр
e — DF°обр
Fe2+ = DF°реакции (1.17),
1/2 DF°обр H2 — DF°обр H+ — DF°обр e = DF°реакции (1.18)
После сложения этих двух уравнений обнаруживается, что
DF°реакции (1.17) + DF°реакции (1.18) = DF°реакции (1.16).
Таким образом, сумма изменений свободной энергии реакции полуэлементов равна изменению свободной энергии всей реакции. Заметим, в частности, что величина DF°обр e при сложении полуреакций сокращается.
Вследствие этого действительная величина DF°обр e не имеет значения, поскольку при сложении свободных энергий двух любых полуэлементных реакций она сокращается. Следовательно, мы можем считать, что DF°обр e равна нулю. А поскольку DF°обр H+ также равна нулю согласно условию
H+водн + e = 1/2 H2 газ,
то
1/2 DF°обр
H2 — DF°обр
H+ = DF°реакции,
0 — 0 = 0.
Стандартная свободная энергия водородного полу элемента равна нулю. Таким образом, любую окислительно-восстановительную реакцию можно выразить в виде двух полуреакций, из которых водородная полуреакция выступает как восстанавливаемая или окисляемая часть этих двух составляющих; изменение же стандартной свободной энергии целиком отвечает либо окислительному, либо восстановительному полуэлементу без учета DF°обр электрона. Данное утверждение можно пояснить на следующем примере. Для реакции
| Fe2+водн + Cu2+водн = Fe3+водн + Cu+водн. | (1.19) |
мы можем написать
| Fe2+водн =
Fe3+водн +
e, Cu2+водн + e = Cu+водн, |
(1.20) (1.21) |
| DF°обр Fe3+ — DF°обр Fe2+ = DF°реакции (1.20), | |
| DF°обр Cu+ — DF°обр Cu2+ = DF°реакции (1.21), | |
| DF°реакции (1.20) + DF°реакции (1.21) = DF°реакции (1.19), | |
где DF°реакции (1.20) и DF°реакции (1.21) - изменения стандартных свободных энергий соответствующих полуреакций. Таким образом, зная ряд изменений стандартных свободных энергий для некоторых полуреакций, мы можем взять любую из выбранных нами пар и получить общее изменение свободной энергии окислительно-восстановительной реакции.
Этот вывод позволяет установить соотношение между свободной энергией реакции и измеренным напряжением гальванического элемента. Предположим, что у нас имеется электрод из чистой меди, погруженный в раствор, который содержит ионы окисной меди с активностью, равной единице, а также водородный электрод, состоящий из инертного платинового электрода, погруженного в раствор с активностью водородного иона, равной единице, и насыщенный по отношению к газообразному водороду с давлением 1 атм (активность также равна единице).
Если электроды соединить, то по цепи потекут электроны. На медном электроде благодаря разрядке ионов окисной меди будет отлагаться медь:
Cu2+водн + 2e = Cuкрист,
а на водородном электроде водород будет терять электроны и превращаться в ионы Н+:
H2 газ = 2H+водн + 2e.
Таким образом, полная реакция примет вид
Cu2+водн + H2 газ = Cuкрист + 2H+водн.
Напряжение между электродами может быть измерено в самом начале реакции, до того как в ходе реакции произойдет сколько-нибудь заметное изменение активностей; оно составит примерно 0,337 в. По мере прохождения реакции напряжение будет снижаться, а при достижении равновесия - станет равным нулю.
Таким образом, в начале реакции напряжение соответствует напряжению реакции, протекающей в стандартных условиях при активности всех веществ, равной единице; в конце реакции, когда изменение свободной энергии равно нулю, напряжение исчезает. Это предполагает наличие связи между напряжением и изменением стандартной свободной энергии, которая может быть выражена соотношением
| DF°реакции = nE°Б | (1.22) |
Здесь Е° - величина напряжения реакции при активности всех веществ, равной единице, n - число участвующих в реакции электронов (в приведенном случае для медно-водородного элемента оно равно двум), а Б - константа (число Фарадея). Число Фарадея равно 23,06 ккал/вЧгЧэкв. Выражение числа Фарадея в таких единицах соответствует другим используемым единицам измерения.
Ниже приведено уравнение, связывающее Е° непосредственно с константой равновесия в стандартных условиях:
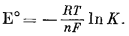 |
(1.23) |
Стандартная свободная энергия реакции водородного полуэлемента равна нулю; соответственно и напряжение этой реакции тоже условно принимается за нуль. Напряжение в любой цепи, когда данный стандартный полуэлемент измеряется относительно стандартного водородного полуэлемента, может быть целиком отнесено за счет данного стандартного полуэлемента и использовано для определения стандартной свободной энергии реакции.
Рассмотрим стандартный электрод металлическая медь - ион окисной меди. Его напряжение, измеренное относительно стандартного водородного электрода, при 298,15° равно 0,337 в; в реакции участвуют два электрона. Из уравнения (1.22)
DF°реакции =
nE°Б,
DF°реакции = 2 ґ 0,337 ґ 23,06 =
15,54 ккал.
Написав реакцию и используя значения DF°обр при 298,15°, получим
Cuкрист = Cu2+водн +
2e,
DF°обр
Cu2+ — DF°обр
Cu = DF°реакции,
15,53
— 0 = 15,53 ккал.
В более общем случае если в уравнение
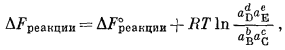 |
(1.13) |
подставим равенства DFреакции = nEБ и DF°реакции = nE°Б, то получим соотношение
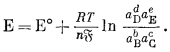 |
(1.24) |
В этом уравнении Е отвечает э. д. с. (электродвижущей силе), или потенциалу. Другими словами, напряжение любого обратимого элемента, характеризуемого химической реакцией
bB + cC = dD + eE,
согласно предыдущему определению Е°, есть э. д. с. элемента в таких условиях, когда активности всех участвующих в реакции веществ равны единице; для системы, находящейся в равновесии, Е = 0.
Для удобства проведения расчетов реакции полуэлементов всегда пишутся так, чтобы продукты окисления и освобожденные электроны помещались в правой части химического уравнения, например
V2O3 крист + H2Oжидк = V2O4 крист + 2H+водн + 2e,
или в общем виде
bВ + cC = dD + eE + ne.
Для реакции, написанной таким образом, потенциал полуэлемента, измеренный относительно стандартного водородного полуэлемента, называется окислительным потенциалом Eh. Один и тот-же символ Е° принято использовать и для реакции стандартного полуэлемента, и для реакции стандартного полного элемента. Таким образом, для полуэлементной реакции
bВ + cC = dD + eE + ne
мы пишем
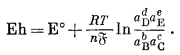 |
(1.24a) |
Для реакций при 25 °С
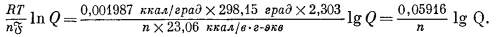
Для примера рассчитаем случай, когда потенциал медного электрода, погруженного в раствор ионов окисной меди, измерен относительно стандартного водородного электрода, но активность ионов окисной меди не равна единице. Здесь мы можем написать
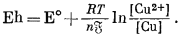 |
(1.25) |
При 25 °С это выражение принимает вид
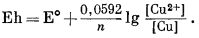 |
(1.26) |
Если измеренный потенциал составляет 0,100 в, активность Сu равна единице, а число участвующих в реакции электронов - двум, то
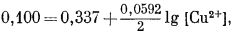 |
(1.27) |
| [Cu2+] = 10—8,03. | |
Выше было приведено определение различных терминов и символов, используемых в последующих главах. В качестве единицы аналитической концентрации компонентов, растворенных в водных растворах, избрана моляльность m; мольная доля N принята в качестве единицы концентрации для твердых растворов, а парциальное давление - за единицу концентрации газов. Активность а - термодинамическая концентрация, определяемая путем термохимических расчетов.
В качестве основы для
дальнейшего рассмотрения равновесных соотношений предложены следующие
немногочисленные уравнения:
1)
Соотношение между константой равновесия и изменением стандартной свободной
энергией реакции
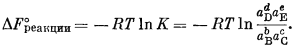
2) Соотношение между квотантом реакции, изменением свободной энергии реакции и изменением стандартной свободной энергии реакции
DF°реакции = DF°реакции + RT ln Q.
3) Соотношение между
изменением стандартной свободной энергии реакции и потенциалом
соответствующего элемента DF°реакции = nЕ°Б.
4) Соотношение
между квотантом реакции, изменением стандартной свободной энергии реакции
и потенциалом соответствующего элемента
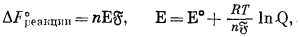
где Е измерено для полуэлемента относительно стандартного водородного полуэлемента и равно окислительному потенциалу Eh.
Применение перечисленных соотношений продемонстрировано на примере реакций различного типа. Избранные примеры относились к реакциям при 25° С и 1 атм, но указанные выше уравнения приложимы и к другим условиям. В последующих главах будут даны расчеты для иных температур и давлений.
1.1. Соляной раствор с
плотностью 1,030 г/см3 содержит 5,03 г
K+ и 15,00 г других твердых веществ, растворенных в 500
г воды. Рассчитайте моляльность, формальность и молярность иона
К+ в этом растворе.
Ответ:
m = 0,257; М = 0,255; f =
0,247.
1.2. Какое из двух веществ — МnО
или Мn(ОН)2 — стабильно при 298,15° и 1 атм общего
давления в присутствии почти чистой
воды?
Ответ: Mn(OH)2 (—3,4
ккал).
1.3. Определите К
при 25° С для реакции СО2 газ + Н2 газ =
С0газ +
Н2Огаз.
Ответ:
К = 10—4,99.
1.4.
Рассмотрим реакцию (при 25° С)
Чему равняется [Н+], если [Sn4+] =
10—10? Какова величина рН этого раствора? Что вы можете сказать
о растворимости касситерита в обычных поверхностных
водах?
Ответ: [Н+] =
10—0,40, рН = 0,40.
1.5.
Подсчитайте э. д. с. элемента, составленного из металлического цинкового
электрода в растворе с [Zn2+] = 10—2,0 и
металлического медного электрода в растворе с [Сu2+] =
10—3,0.
Ответ: Е = 1,07
в.
1.6. Если идет реакция в
элементе из упражнения 1.5, то что происходит с [Cu2+] -
увеличивается или уменьшается?
1По-видимому, точное определение понятия "формальность" (formality) в химической литературе отсутствует. Здесь принято наиболее широко распространенное определение.
2В советской литературе по химической термодинамике специальный термин для обозначения величины Q отсутствует. В работах, написанных на английском языке, нередко употребляется термин quotient (дословно -"частное"), который мы предлагаем переводить словом "квотант".- Прим. ред.
3В том смысле, что реакции между твердыми фазами постоянного состава либо протекают до конца (если DF°реакции < 0), либо не идут совсем (если DF°реакции Ј 0). — Прим. ред.
4Во всех последующих расчетах при 1 атм общего давления мы будем использовать термины "парциальное давление" и "активность" как синонимы; для систем с повышенным общим давлением между этими понятиями будет проводиться различие.
|
|
|