| Р.М. Гаррелс, Ч.Л. Крайст | Растворы, минералы, равновесия |
|
|
|
|
[Содержание] [Глава 1] [Глава 3] |
|
|
|
|
Геохимики в основном имеют дело с такими материалами, как горные породы и природные воды. За немногими исключениями, химическая информация, касающаяся этих объектов, дается в единицах концентрации. В литературе опубликованы десятки тысяч анализов горных пород и минералов и по меньшей мере столько же анализов природных вод.
Однако при расчетах равновесии между минералами или между минералами и природными водами в уравнениях используются (или по ним определяются) величины активности. Таким образом, изучение соотношений между минералами с помощью термохимических расчетов требует перехода от концентраций к активностям и обратно. В общем можно сказать, что соотношения между активностями, найденными путем расчетов, столь же надежны, как надежны и величины концентраций, полученные различными аналитическими методами. Основные ошибки при исследовании природных систем возникают в процессе перехода от концентраций к активностям и обратно.
При анализе соотношений между активностью и концентрацией удобно рассмотреть в определенной последовательности несколько различных типов растворов, встречающихся в практике. Так мы и поступим - начнем с газов, затем перейдем к жидким растворам неэлектролитов, твердым растворам, расплавам и, наконец, обратимся к водным растворам электролитов.
Единственный общий вывод, который можно сделать относительно всех типов растворов, заключается в том, что "подобное растворяет подобное". Так, жидкости, состоящие из нейтральных, неполяризованных молекул типа бензола или толуола, свободно растворяются одна в другой, Вr— — легко замещает часть С1— в кераргирите (AgCl) с образованием твердого раствора и, наконец, все газы смешиваются в любых пропорциях. Вещества, обладающие в твердом состоянии ионным строением, такие, как NaCl, легко растворяются в воде, т. е. в жидкости, характеризующейся высокой диэлектрической константой. Вместе с тем в воде бензол растворим чрезвычайно слабо (как и вода в бензоле); органические соединения не образуют твердых растворов с неорганическими и т. д.
Прежде чем перейти к выводу соотношений между активностью и концентрацией в реальных системах, обычно рассматривают определенные модельные системы. Этот прием использован и в настоящей книге: в качестве моделей избраны идеальный газ, идеальная газовая смесь и идеальный раствор - газообразный, жидкий или твердый. Для перечисленных модельных систем можно вывести четкие и простые соотношения. Тем же закономерностям при различных условиях приблизительно подчиняются и реальные системы, но, что весьма существенно, более близкое соответствие идеальным системам достигается лишь в точно определенных условиях.
Активность идеального газа. Многочисленными экспериментами доказано, что поведение реальных газов при обычных давлениях и температурах может быть приблизительно описано одним предельным законом - уравнением идеального газа, математическое выражение которого имеет следующий вид:
| pV = nRT. | (2.1) |
В частности, при комнатной температуре большинство газов, представляющих интерес для геологов, ведет себя почти идеально до давления по меньшей мере 1 атм. Кроме того, экспериментально доказано, что по мере снижения давления или повышения температуры (если не наблюдаются явления разложения1 (стр.30) ) газ становится более идеальным и в пределе при нулевом давлении поведение газа будет в точности соответствовать уравнению идеального газа. Эта закономерность схематически изображена на Рис. 2.1. Здесь предполагается, что данная масса газа в n молей, занимающая общий объем V t, имеет возможность постепенно расширяться при постоянной температуре. В ходе этого процесса время от времени измеряется мольный объем Vизм = V tизм/n и одновременно регистрируется давление Ризм. Затем находится соответствующая расчетная величина Ррасч, для чего используется выражение
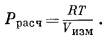 |
(2.2) |
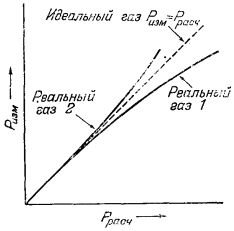 |
| Рис. 2.1. Поведение двух различных реальных газов и поведение идеального газа при постоянной температуре. |
На Рис. 2.1 графически показано соотношение величин Ррасч и Ризм для реальных газов двух различных типов. Штриховая линия с наклоном 45° отражает случай, когда Ррасч = Ризм, и соответствует идеальному газу. Кривая соотношения Ризм и Ррасч для реального газа может лежать выше или ниже этой прямой (или, что также возможно, пересекать прямую идеального газа при повышенных давлениях), но в любом случае с приближением к нулевому давлению наклон кривой будет приближаться к наклону прямой идеального газа.
Принято считать, что активность идеального газа в стандартном состоянии, т. е. при 1 атм и некоторой температуре, равна единице. Вообще же для идеального газа активность (безразмерная величина) считается численно равной давлению, выраженному в атмосферах, вне зависимости от величины самого давления. Итак, для идеального газа
| a = |P(атм)|. | (2.3) |
А к т и в н о
с т ь р е а л ь н ы х г а з о в; к о
э ф ф и ц и е н т а к т и в н о с т и. Как и следует ожидать, в
случае реальных газов урав-
|
1 (стр.30) Если молекулы газа при повышенной температуре диссоциируют на молекулы меньшего размера или на отдельные атомы, но при этом увеличение количества частиц, в системе учтено и отражено величиной n, то уравнение идеального газа PV = nRT для этого случая останется справедливым. Данная газовая система будет представлять собой идеальную газовую смесь, описанную ниже. |
нение (2.3) в общем оказывается несправедливым. В соответствии с этим мы будем использовать другое соотношение:
| a = cP(атм). | (2.4) |
Величина c называется коэффициентом активности газа; для любого данного газа она зависит от температуры и давления. Поскольку реальный газ приближается к идеальному при пониженном давлении, c любого газа при низких давлениях близок к единице. Эта особенность отражена на Рис. 2.2, где приведены коэффициенты активности некоторых газов при
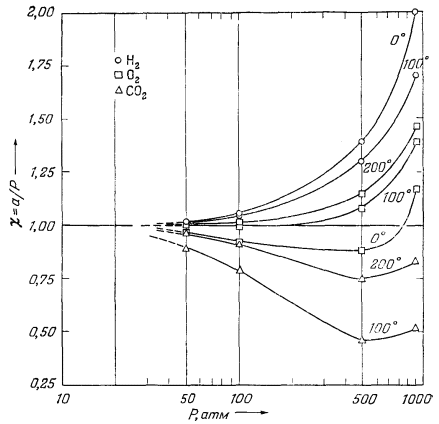 |
| Рис. 2.2. Зависимость коэффициентов
активности некоторых важных газов от температуры и
давления. Давление выражено в атмосферах и дано в логарифмической шкале [3, стр. 210]. |
разных температурах и при давлениях до 1000 атм. Анализ Рис. 2.2 показывает, что при давлениях, не превышающих примерно 10 атм, c для всех рассматриваемых газов существенно не отличается от единицы. Эта особенность представляет значительный практический интерес, так как она позволяет нам при термохимических расчетах с газами при умеренно высоких давлениях подставлять численные величины давления вместо активностей.
Давление, рассчитанное на основании уравнения идеального газе по уравнению (2.2):
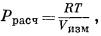
не следует путать с активностью, как это часто делают. Фактически для умеренных давлений соотношение между Ррасч и а довольно точно определяется выражением
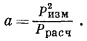 |
(2.5) |
Из уравнения (2.5) следует, что а и Ррасч отклоняются от Ризм в противоположные стороны. Например, если для некоторого газа Ризм равно 10 атм, а Ррасч равно 10,5 атм, то
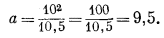
В итоге, по мере того как Ризм приближается к нулю, а и Ррасч с двух сторон приближаются к Ризм.
Для газов типа кислорода зависимость, выражаемая уравнением (2.5), достаточно точно выдерживается до давлений порядка 100 атм; в случае таких неидеальных газов, как СО2, расхождение не превышает 4% до давления 50 атм (Рис. 2.2). Таким образом, если для какого-либо газа известны давление и мольный объем, то нетрудно подсчитать и его активность.
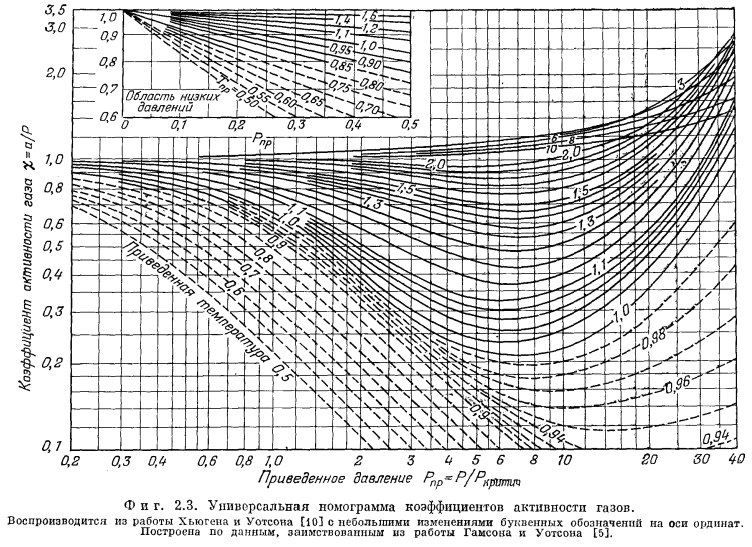
Для коэффициентов активности газов как функции температуры и давления можно построить универсальную номограмму, воспользовавшись "приведенными" температурами и давлениями. Такая номограмма изображена на Рис. 2.3. "Приведенная" температура - это отношение интересующей нас . температуры к критической температуре газа в градусах Кельвина. "Приведенное" давление определяется отношением интересующего нас давления к критическому давлению газа. Необходимые величины критических констант для ряда веществ приведены в табл. 2.1.
В качестве примера пользования номограммой (Рис. 2.3) рассчитаем активность газообразного кислорода при температуре 473° К и давлении
Таблица 2.1
| Газ | Критическая температура, °С | Критическая температура, °К | Критическое давление, атм | Плотность, г/cм3 |
| СОз | 31,1 | 304,3 | 73,0 | 0,460 |
| CS2 | 273 | 546 | 76 | — |
| СО | —139 | 134 | 35 | 0,311 |
| COS | 105 | 378 | 61 | — |
| Сl2 | 144,0 | 417,2 | 76,1 | 0,573 |
| Не | —267,9 | 5,3 | 2,26 | 0,0693 |
| Н2 | —239,9 | 33,3 | 12,8 | 0,0310 |
| НВr | 90 | 363 | 84 | — |
| НСl | 51,4 | 324,6 | 81,6 | 9,42 |
| HI | 151 | 424 | 82 | — |
| H2Se | 138 | 411 | 88 | — |
| H2S | 100,4 | 373,6 | 88,9 | — |
| Hg | >1550 | >1823 | >200 | 4—5 |
| CH4 | —82,5 | 190,7 | 45,8 | 0,162 |
| N2 | —147,1 | 126,1 | 33,5 | 0,311 |
| O2 | —118,8 | 154,4 | 49,7 | 0,430 |
| SiF4 | —1,5 | 271,7 | 50 | — |
| SiH4 | —3,5 | 269,7 | 48 | — |
| SnCl4 | 318,7 | 591,9 | 37,0 | 0,742 |
| S | 1040 | 1313 | — | — |
| SO2 | 157,2 | 430,4 | 77,7 | 0,52 |
| SO3 | 218,3 | 491,5 | 83,6 | 0,630 |
| Н2О | 374,0 | 647,2 | 217,7 | 0,4 |
1000 атм. Для этого случая приведенная температура равна
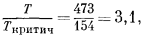
а "приведенное" давление
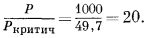
Согласно полученным величинам, по номограмме находим, что величина c приблизительно равна 1,5. Это значение прекрасно соответствует более точно определенному c для O2 по Рис. 2.2 (1,4б).
Точность нахождения величин c по универсальной номограмме коэффициентов активности (Рис. 2.3) будет зависеть от величины приведенных температуры и давления; она будет различной для разных газов.
Подразумевается, что однокомпонентный идеальный газ, подчиняющийся уравнению PV = nRТ, обладает молекулярной структурой, т. е. состоит из свободно движущихся молекул бесконечно малого объема, не обнаруживающих сколько-нибудь заметного взаимодействия. Такое представление находится в соответствии с наблюдаемым фактом: с понижением давления реальные газы по своему поведению приближаются к идеальным. Поскольку по мере снижения давления число молекул газа в данном его объеме уменьшается, то и суммарный объем самих молекул, приходящийся на данный объем газа, становится все менее существенным. А так как среднее расстояние между молекулами газа при понижении давления увеличивается, то и силы взаимодействия между ними уменьшаются.
А к т и в н о с т ь и д е а л ь н о й г а з о в о й с м е с и. Рассмотрим идеальную газовую смесь, для которой справедливы приведенные выше рассуждения относительно молекулярной структуры однокомпонентного идеального газа. Идеальной газовой смесью называется смесь газов, подчиняющаяся уравнению состояния идеального газа, PV = nRT, в котором в качестве множителя n теперь выступает суммарное число молей всех газов, входящих в состав данной смеси. Уравнение состояния идеальной газовой смеси определяется выражением
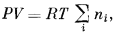 |
(2.6) |
где
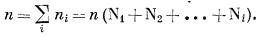 |
(2.7) |
Активность каждого компонента идеальной газовой смеси зависит только от относительного количества молекул данного компонента, присутствующих в смеси, т. е. от его мольной доли. Поэтому, согласно уравнению (2.3),
| ai = |PNi|, | (2.8) |
т. е. активность компонента i идеальной газовой смеси численно определяется величиной общего давления (в атмосферах), умноженной на мольную долю компонента i.
Следующее выражение, применимое для любых газов, связывает парциальное давление каждого компонента с общим давлением:
| Pi = PNi, | (2.9) |
а так как, согласно уравнению (2.9),
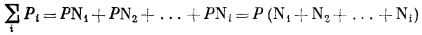
и
N1 + N2 + ... + Ni = 1,
то
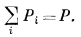 |
(2.10) |
Другими словами, сумма парциальных давлений всех газов, участвующих в смеси, равна общему давлению.
Сопоставление уравнений (2.8) и (2.9) показывает, что для идеальной газовой смеси
| ai = |Pi|. | (2.11) |
Для реальных газовых смесей уравнение (2.11) неприменимо.
А к т и в н о с т ь и д е а л ь н о г о г а з о в о г о р а с т в о р а. Насколько известно, все газы образуют друг с другом однородные смеси в любых пропорциях. По своему поведению смеси реальных газов, как и однокомпонентные реальные газы, отличаются от идеального газа. Однако для большинства газов еще мало известно о влиянии одного компонента смеси на активность другого компонента, входящего в состав газового раствора. И поэтому реальные газовые растворы обычно рассматриваются как идеальные растворы. Такое допущение прежде всего означает, что каждый газ, присутствующий в газовом растворе, ведет себя независимо от прочих газовых составляющих раствора и что каждый газ входит в газовую смесь с такими же отклонениями от идеального состояния, какими он характеризовался, будучи чистым газом1 (стр.35) . Соответственно для идеального газового раствора активность газообразного компонента i определяется выражением
| ai = ciPNi, | (2.12) |
где Р - общее давление (в атмосферах), ci - коэффициент активности данного газового компонента при общем давлении Р (и при данной температуре), a Ni - мольная доля компонента.
В качестве частного примера рассчитаем активность кислорода в смеси 2 моль кислорода и 6 моль азота при общем давлении 500 атм и температуре 120° С. Мольная доля кислорода равна
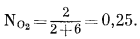
Величина коэффициента активности кислорода определяется коэффициентом активности чистого кислорода при общем давлении данной смеси. Пользуясь табл. 2.1, находим приведенную температуру
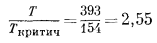
и приведенное давление
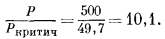
|
1 (стр.35) Без многократной проверки такого допущения мы не можем с уверенностью говорить о правильности расчетов, сделанных па его основании. Однако для большинства газов, интересующих геологов, имеющиеся к настоящему времени данные указывают на то, что наиболее серьезные ошибки, связанные с этим допущением, возникают в тех случаях, когда плотность газа близка к критической плотности какого-либо компонента, т. е. примерно равна 0,4 г/см3. При плотности, более высокой или более низкой, чем критическая, поведение газового раствора может ближе соответствовать идеальному. |
По Рис. 2.3 определяем, что cO2 равен 1,1. Подставив это значение в уравнение (2.12), получаем
aO2 = 1,1 ґ 500 ґ 0,25 = 138.
Только знание химии газовой смеси позволит решить, можно ли рассматривать такую смесь как идеальный раствор. С одной стороны, имеются смеси, например кислорода и аргона, к которым можно с уверенностью подходить как к идеальным. Совсем иначе ведет себя газовая смесь серы и кислорода. Дело не только в том, что газообразная сера состоит из нескольких различных молекул серы, относительное содержание которых меняется в зависимости от температуры, но еще и в том, что эти молекулы взаимодействуют с кислородом с образованием таких молекул, как SO, SO2 или SO3.
При обычных температурах и давлениях, не превышающих по меньшей мере 1 атм, поведение чистых газов примерно подчиняется уравнению состояния идеального газа, PV = nRT. В таких условиях активность газа может численно приравниваться давлению, выраженному в атмосферах. Газовые смеси в интересующем нас температурном диапазоне и при давлении от 0 до 1 атм ведут себя как идеальные газовые смеси. Для таких смесей активность каждого участвующего в смеси газа принимается численно равной его парциальному давлению.
При повышенных давлениях газовые растворы рассматриваются как идеальные, если известно, что между газовыми компонентами раствора химическое взаимодействие отсутствует. Для таких растворов активность каждого компонента может определяться аналитически и графически. В тексте приведена номограмма (Рис. 2.3), которая позволяет находить коэффициенты активности по приведенным температурам и давлениям газов. Активность данного компонента в идеальном газовом растворе определяется произведением трех величин: коэффициента активности соответствующего чистого газа при общем давлении смеси, общего давления в атмосферах и мольной доли этого компонента.
Растворами неэлектролитов называются такие растворы, которые состоят из незаряженных частиц. Типичные бинарные растворы неэлектролитов могут быть образованы различными парами органических жидкостей, например бензолом и толуолом. Изучение поведения растворов неэлектролитов, в общем несложного и наглядного из-за простоты кинетических явлений, непосредственно подводит к некоторым фундаментальным представлениям, в том числе и к ясному определению понятия "активность". Теория растворов неэлектролитов сначала была распространена на молекулярные растворы, а теперь нашла применение и при изучении растворов металлов. Более того, та же теория описывает поведение твердых растворов и растворов расплавленных солей даже в тех случаях, когда в растворах присутствуют ионы. Следовательно, теория растворов неэлектролитов применима ко всем растворам, с которыми имеет дело геолог, за исключением водных растворов электролитов. Эта теория справедлива для твердых растворов в минералах, явлений катионного обмена, магматических процессов л для органических веществ, как твердых, так и жидких.
З а к о н Р а у л я. Установлено, что многие бинарные жидкие растворы неэлектролитов характеризуются (с различной степенью точности) простым соотношением между давлением пара каждого компонента раствора и мольной долей этого компонента в растворе. Это соотношение, называемое законом Рауля, определяется следующим уравнением:
| Pi = P*iNi. | (2.13) |
Здесь Рi - равновесное давление пара1 (стр.37) компонента i раствора, Ni - мольная доля этого компонента в растворе, а Р*i - равновесное давление пара
 |
 |
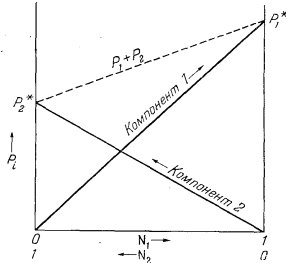
| Ф и г. 2.4. Зависимость
давления пара Pi от мольных долей
Ni для бинарной системы, подчиняющейся закону
Рауля. P*1 и P*2 отвечают давлениям паров двух рассматриваемых веществ в чистом состоянии. Штриховой линией показано общее давление над раствором, создаваемое парами обоих веществ и зависящее от состава раствора. |
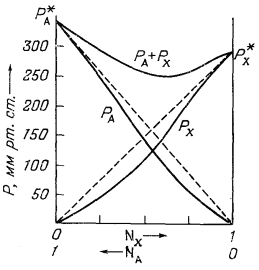
Ф и г. 2.5. Зависимость
парциальных давлений от состава в системе хлороформ - ацетон при
35,2° С. Сплошные линии, обозначенные буквами РA и РX - это кривые давления пара для ацетона и хлороформа соответственно; штриховыми линиями показано поведение, отвечающее закону Рауля [30]. |
чистого вещества i. Поскольку величина давления пара зависит от изменения температуры и общего давления, закон Рауля приложим только к условиям постоянной температуры и постоянного общего давления.
Уравнение (2.13) применимо к раствору с любым числом компонентов. Для бинарного раствора мы можем составить систему из двух уравнений:
| P1 = P*1N1, | (2.14a) |
| P2 = P*2N2. | (2.14б) |
Графически эта система уравнений изображена на Рис. 2.4.
Чем ближе компоненты
раствора друг к другу по своим физическим свойствам, тем лучше этот
раствор подчиняется закону Рауля. Так, растворы жидких органических
оптических изомеров и растворы изотопов ведут себя почти в точном
соответствии с законом Рауля. Однако для большинства растворов
обнаруживаются отклонения и иногда довольно значительные. В качестве
примера на Рис. 2.5 приведена диаграмма, показывающая соотношения между
давлением пара и составом для системы ацетон - хлороформ. Нетрудно видеть,
что для этой системы установлено отрицательное
|
1 (стр.37) Давление насыщенного (насыщающего) пара. — Прим. ред. |
отклонение от закона Рауля. Заметим, что в различных системах наблюдаются как положительные, так и отрицательные отклонения от этого закона.
Если раствор подчиняется закону Рауля, а пары компонентов раствора ведут себя как идеальный газ, то такой раствор принято считать идеальным. Следовательно, для идеального раствора
| P'i = P*'iNi; | (2.15) |
штрихи у символов давления указывают, что пары данного компонента ведут себя в соответствии с законом идеального газа.
Ф у г и т и в н о с т ь (л е т у ч е с т ь). Давление идеального газа играет важнейшую роль в химической термодинамике и имеет специальное название - фугитивность (буквенный символ fi). На основании этого определения
| P'i = f'i. | (2.16) |
Сочетание уравнений (2.15) и (2.16) дает выражение
| fi = f*iNi, | (2.17) |
справедливое для идеального раствора.
Большая часть растворов при обычных температуре и общем давлении характеризуется относительно низким давлением паров. При столь низких давлениях пары по своему поведению приближаются к идеальному газу. В таких условиях фугитивность и измеряемое давление пара практически равны между собой, т. е.
Pi 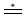 fi (символ fi (символ 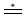 означает примерное равенство). означает примерное равенство). |
(2.17а) |
Для таких температур и давлений, когда данный пар ведет себя отлично от идеального газа, величина фугитивности будет отличаться от измеряемого давления пара. Однако всегда есть возможность вывести одну величину из другой; фугитивность в таких случаях можно рассматривать как корректированное давление.
Следует отчетливо себе представить, что фугитивность компонента, растворенного в любой конденсированной фазе (жидкой или твердой), равна фугитивности этого компонента в газовой фазе, находящейся в равновесии с данной конденсированной фазой. Хотя понятие фугитивности выведено здесь при рассмотрении идеального раствора и идеального газа, фугитивность растворенного компонента в любом растворе, даже неидеальном, представляет собой определенную и обычно измеряемую величину.
С о о т н о ш е н и я м е ж д у а к т и в н о с т ь ю и ф у г и т и в н о с т ь ю. Имея в виду вышесказанное, можно перейти к выводу фундаментального определения активности растворенного компонента в любом растворе. Активность ai определяется выражением
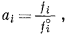 |
(2.18) |
где fi - фугитивность растворенного компонента i, a f°i - фугитивность того же компонента в стандартном состоянии. За стандартное состояние жидкого или твердого вещества обычно принимается чистая жидкость или твердое вещество при 1 атм общего давления и определенной температуре. Для таких стандартных условий фугитивность компонента в стандартном состоянии (стандартная фугитивность) равна фугитивности чистого вещества, т. е.
| f°i = f*, | (2.19) |
а поэтому уравнение (2.18) принимает вид
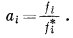 |
(2.20) |
В этих последних уравнениях (если учесть, что звездочкой обозначают чистое вещество, что фугитивность измеряется в единицах давления - атмосферах, барах, миллиметрах ртутного столба и т. д.- и что размерности давления сокращаются, поскольку активность есть отношение давлений) активность выражается безразмерной величиной. Кроме того, следует обратить внимание на то, что для чистого вещества
fi = f*i
а, исходя из уравнения (2.20),
a*i = l.
Другими словами, активность чистого вещества в стандартном состоянии при отмеченных выше условиях равна единице.
Уравнение (2.20) справедливо для любого раствора. В случае идеального раствора на основании уравнений (2.20) и (2.17) мы можем получить следующее важное отношение:
| ai = Ni. | (2.21) |
Для идеального бинарного раствора справедлива такая система сопряженных уравнений:
| a1 = N1, | (2.22a) |
| a2 = N2, | (2.22б) |
Графическое изображение уравнений (2.22а) и (2.22б) приведено на Рис. 2.6.
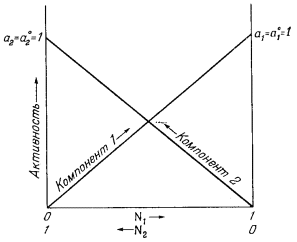 |
| Ф и г. 2.6. Диаграмма активность - состав для идеального бинарного раствора при 1 атм общего давления и данной температуре (состав выражен в мольных долях). |
Из уравнения (2.20) следует, что активность любого растворенного компонента можно установить путем определения равновесного давления пара данного компонента над раствором. Если пар ведет себя как идеальный газ, то его фугитивность будет равна парциальному давлению; если же пар не подчиняется закону идеального газа, то фугитивность можно рассчитать по давлению пара, о чем речь пойдет ниже. Следовательно, практически путь определения активности веществ, характеризующихся значительным давлением пара (таких, как ранее упоминавшаяся система хлороформ - ацетон или вода в самых различных водных растворах), лежит через определение давления пара. Для менее летучих компонентов, вроде МgСО3, растворенного в СаСО3 при комнатной температуре, т. е. такой системы, оба компонента которой характеризуются ничтожно малым давлением пара, уравнение (2.20) использовать нельзя. В этом случае для определения активностей нужно обратиться к другим косвенным методам.
Уравнение (2.18) имеет более общую форму и применимо ко всем состояниям вещества - твердому, жидкому или газообразному. Для газа, за стандартное состояние которого принят чистый газ при фугитивности, равной единице, из уравнения (2.18) получаем
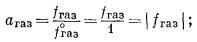 |
(2.23) |
это означает, что активность газа численно равна его фугитивности (размерности давления у фугитивностей сокращаются).
В предыдущем разделе, где рассматривались соотношения между активностью и концентрацией газов, было описано несколько методов определения активности по давлению и составу. Согласно уравнению (2.23), активность и фугитивность для газа численно равны между собой. Следовательно, в ранее выведенных для газов уравнениях (2.3), (2.5), (2.8), (2.11), (2.12) вместо активности мы всюду можем подставить величину фугитивности. При этом надо лишь помнить, что в каждом уравнении фугитивность необходимо выражать в тех же единицах, что и давление (в атмосферах). Следует обратить внимание на то, что активность и фугитивность численно равны между собой только для газов. Согласно уравнениям (2.18) и (2.20), активность жидких и твердых веществ всегда определяется отношением фугитивностей, а знаменатель в этом отношении не равен единице (за редким исключением). Итак, всегда существует возможность вывести фугитивность пара по его давлению; на этом мы закончим разбор практического определения понятия "активность", данного уравнением (2.18).
Обратимся к Рис. 2.5, чтобы продемонстрировать важность только что введенных величин. Измеренное давление пара чистого ацетона Р*A (при 35,2° С) равно 344 мм рт. ст.; та же величина для чистого хлороформа, РХ, равна 293 мм рт. ст.1 (стр.40). Разумно предположить, что при столь низких давлениях эти чистые пари ведут себя как идеальный газ. Следовательно, в данном случае давление равно фугитивности. Согласно уравнению (2.17а), для чистого хлороформа
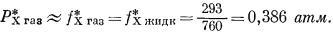
Активность пара хлороформа, находящегося в равновесии с чистым жидким хлороформом, определяется по уравнению (2.23)
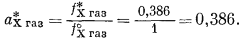
Согласно уравнению (2.18), активность чистого жидкого хлороформа равна
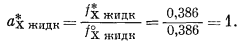
При мольной доле ацетона в растворе, равной 0,419, общее измеренное давление составляет 248 мм рт. ст. Если бы раствор ацетона и хлороформа подчинялся закону Рауля (а парциальные давления паров были аддитивными), то для данного Состава по уравнению (2.13) общее давление пара было бы равно
Робщее = РA + РX = P*A NA + Р*Х NХ = 344 ґ 0,419 + 293 ґ 0,581 = 314 мм рт. cт.
Отсюда ясно, что данный раствор характеризуется
отрицательным отклонением от закона Рауля.
|
1 (стр.40) Цифровые данные для системы ацетон - хлороформ взяты из работы Завидски [30]. |
Рассчитаем фугитивность и активность ацетона на том же примере раствора ацетона и хлороформа с составом NA = 0,419 и NX = 0,581. Вновь начнем с уравнения (2.17а):
PA 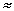 fA
fA
Измеренное давление пара ацетона над раствором данного состава равно 108 мм. Фугитивность его составит
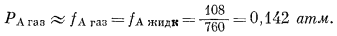
Активность ацетона в газовой фазе, согласно уравнению (2.23), равна
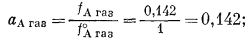
активность ацетона в жидкой фазе, определяемая по уравнению (2.18), составляет
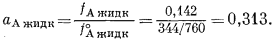
Если бы система ацетон-хлороформ давала идеальный раствор, то активность ацетона в растворе, согласно уравнению (2.21), была бы равна
aА жидн = NА жидк = 0,419.
В л и я н и е д а в л е н и я н а ф у г и т и в н о с т ь и а к т и в н о с т ь. Поскольку многочисленные физические и химические превращения, интересующие геологов, происходят при давлениях, значительно превышающих 1 атм, мы должны обсудить и такой вопрос: как меняется активность с изменением общего давления1 (стр.41) . Для чистых газов и газовых растворов такой проблемы не существует, ибо в этом случае уравнения активности учитывают общее давление. Однако в отношении жидких и твердых растворов данная проблема весьма настоятельна.
В нашем фундаментальном определении активности соотношение (2.18)
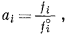
относилось ко всем температурам и давлениям. В этом выражении величина fi° представляет собой фугитивность компонента i в его стандартном состоянии. За стандартное состояние принято чистое жидкое или твердое вещество при определенной температуре и 1 атм общего давления. Отсюда следует, что fi° не меняется с изменением общего давления. Однако fi, а соответственно и аi; меняются в зависимости от давления; эта зависимость определяется уравнением (2.24)
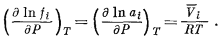 |
(2.24) |
Согласно уравнению (2.24),
скорость изменения ln аi (или ln fi) с
изменением общего давления (при постоянной температуре) равна парциальному
мольному объему компонента i, деленному на RT.
|
1 (стр.41) Жидкость или твердое вещество, находящиеся в открытом сосуде, испытывают давление, равное приблизительно 1 атм (в зависимости от барометрического давления в данный момент). Повышенное давление может сообщаться жидкости или твердому веществу посредством поршня; в таком случае газовая фаза будет отсутствовать. Однако и здесь можно рассчитать мнимое давление пара, измеряемое силой бомбардировки поршня молекулами. С другой стороны, повышенное давление на жидкость или твердое вещество можно создать с помощью какого-либо инертного газа, сжимаемого до заданного давления в замкнутом пространстве над жидкостью или твердым веществом. |
Использование уравнения (2.24) можно продемонстрировать на примере воды. Для этого случая можно написать
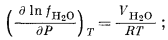 |
(2.25) |
здесь VH2O — объем 1 моль чистой воды при данной температуре Т и при любом из рассматриваемых давлений. Частное интегрирование уравнения (2.25) дает следующий результат:
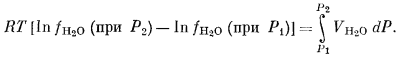 |
(2.26) |
Попросту говоря, правая часть уравнения (2.26) представляет собой поле ниже кривой зависимости VH2O от Р. Поскольку величины VH2O при различных давлениях определены экспериментально, мы можем решить уравнение (2.26) и тем самым получить значения фугитивности и активности воды при любой данной температуре. В табл. 2.2 приводятся значения активности и фугитивности при температуре 298° К. Следует обратить внимание на то, что в табл. 2.2 для каждого давления активность определяется путем
Таблица 2.2
| Давление, атм |
Фугитивность, атм |
Активность | Давление, атм |
Фугитивность, атм |
Активность |
| 1 | 0,03125 | 1 | 600 | 0,04838 | 1,5481 |
| 100 | 0,03362 | 1,0757 | 700 | 0,05199 | 1,6637 |
| 200 | 0,03618 | 1,1576 | 800 | 0,05586 | 1,7874 |
| 300 | 0,03892 | 1,2454 | 900 | 0,06000 | 1,9200 |
| 400 | 0,04186 | 1,3394 | 1000 | 0,06443 | 2,0618 |
| 500 | 0,04501 | 1,4402 |
деления фугитивности при данном давлении на фугитивность при 1 атм, т. е. в соответствии с уравнением (2.18). Так, при 500 атм общего давления
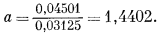
Подобные расчеты можно проделать для любой системы, если
только имеются данные по значениям 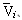
Как было показано выше, f*i меняется в зависимости от давления, a f°i не меняется; поэтому зависимость, определяемая уравнением (2.19), справедлива только для давления в 1 атм. Следовательно, уравнения (2.20) и (2.21) также справедливы только для 1 атм. При давлениях, отличных от 1 атм, для определения идеального раствора мы имеем право пользоваться лишь уравнением (2.17):
fi = f*i Ni.
Чтобы получить выражение активности идеального раствора при давлениях, отличающихся от 1 атм, подставим равенство (2.17) в уравнение (2.18):
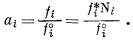 |
(2.27) |
С помощью выведенного уравнения (2.27) в качестве примера рассчитаем активность гипотетического идеального водного раствора при давлении 1000 атм и температуре 298° К. Согласно данным табл. 2.2, при NH2O = 1 f*H2O будет равно 0,06443, а поскольку f°H2O = 0,03125, для нашего идеального раствора из уравнения (2.27) получаем
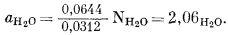 |
(2.27a) |
Графически величина aH2О для разных NH2O в данной системе изображена на Рис. 2.7.
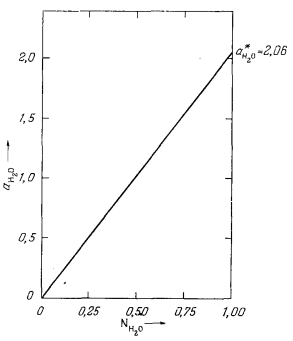 |
| Ф и г. 2.7. Зависимость активности воды от состава гипотетического идеального водного раствора неэлектролита при давлении 1000 атм и 298° К. |
Следует обратить внимание на то, что мы не учитываем изменения фугитивности или активности в зависимости от температуры. Хотя можно вывести уравнение, описывающее зависимость подобного рода, но участвующие в нем переменные в общем измерить труднее, чем саму фугитивность или активность. Итак, мы будем считать, что фугитивность или активность известны или что они могут быть измерены для каждой данной температуры.
Р а ц и о н а л ь н ы
й к о э ф ф и ц и е н т а к т и в н о с
т и. Большая часть реальных растворов ведет себя неидеально. Тем не менее
положения, выведенные для идеальных растворов, могут быть полезны при
исследовании свойств реальных растворов.
 |
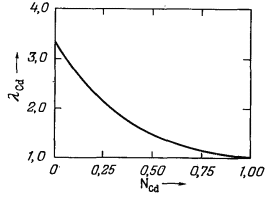 |
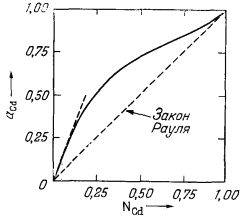
| Рис. 2.8. Активность кадмия в системе Cd - Рb при 500° С и 1 атм [4]. | Рис. 2.9. Коэффициенты активности кадмия в системе Cd - Рb при 500° С и 1 атм давления. |
В качестве примера рассмотрим соотношение активности и состава в реальном растворе, показанное на Рис. 2.8. Этот график построен для жидкого раствора кадмия и свинца при 500° С и 1 атм. Следует отметить, что активность Cd при низких концентрациях значительно превышает соответствующие мольные доли; другими словами, в этом случае мы встречаемся с большим положительным отклонением от закона Рауля. Если же мольная доля Cd становится равной единице, активность этого элемента также будет равна единице.
Чтобы законы, выведенные для идеальных растворов, могли быть использованы и для неидеальных систем, необходимо вновь обратиться к коэффициенту активности. Для растворов неэлектролитов предлагается ввести понятие рационального коэффициента активности, значение которого при всех температурах и давлениях определяется выражением
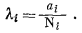 |
(2.28) |
Значения коэффициента активности в зависимости от мольной доли Cd в системе Cd - Рb получить нетрудно - нужно лишь разделить каждую величину активности на соответствующую величину мольной доли. Так, исходя из Рис. 2.8, при NCd = 0,50 aCd = 0,72; поэтому
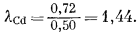
График зависимости значений lCd от NCd приведен на Рис. 2.9. Необходимо обратить внимание на следующее: поскольку aCd приближается к единице с приближением к единице NCd (Рис. 2.8), то и lCd тоже становится равным единице.
Для идеального раствора при давлении 1 атм и данной температуре li = 1. Однако при давлениях, отличных от 1 атм, в случае идеального раствора li № 1. Согласно уравнению (2.27),
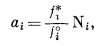
а поскольку из уравнения (2.28) в общем следует, что
ai = liNi,
то получаем
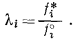 |
(2.29) |
Так как величина f°i не зависит от давления, a f*i постоянна для рассматриваемого давления, в случае идеального раствора li будет иметь различное, но постоянное значение для каждого давления. Это значение будет равно единице при давлении 1 атм и отличаться от единицы при давлениях выше или ниже 1 атм.
Таким образом, для ранее рассмотренного примера с гипотетическим водным раствором при 298° К и 1000 атм давления [уравнение (2.27а) lН2О будет постоянной величиной, равной 2,06.
З а к о н Г е н р и. Чем дальше мы углубляемся в существо вопроса, тем настоятельней становится необходимость разграничить понятия "растворенное вещество" и "растворитель" (растворяющее вещество, сольвент). Это разграничение приобретает смысл лишь в том случае, когда компонент, называемый растворенным, присутствует в растворе в относительно небольшой пропорции по отношению к растворителю, т. е. когда мы имеем дело с разбавленными растворами.
Установлено, что для реальных растворов неэлектролитов во всех случаях без исключения степень пропорциональности изменения фугитивности растворенного компонента f2 относительно изменения мольной доли N2 возрастает по мере разбавления раствора, т. е. с приближением N2 к нулю (при постоянных температуре и общем давлении). Математически это правило выражается следующим уравнением:
| f2 = k"N2 при N2 ® 0. | (2.30) |
Уравнение (2.30) известно как закон Генри.
Различие между выражениями закона идеального раствора и закона Генри заключается в разной величине коэффициента пропорциональности, вводимого в эти выражения, что хорошо видно при сравнении уравнений (2.17) и (2.30):
| идеальный раствор | f2 = f*2N2, | (2.17) |
| закон Генри | f2 = k"N2. | (2.30) |
Причину расхождения между этими двумя формулами объясняет диаграмма, приведенная на Рис. 2.10. Величина коэффициента пропорциональности k" и пределы применимости закона Генри зависят от особенностей растворенного вещества и растворителя, а также от температуры и общего давления.
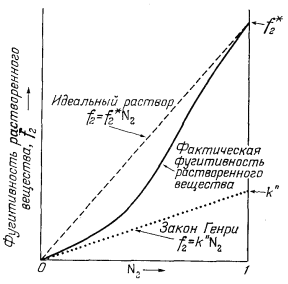 |
| Ф и г. 2.10. Схематическая диаграмма, показывающая различие между законом Генри и законом идеального газа для реального бинарного раствора. |
Если обе части уравнения (2.30) разделить на f°2 - фугитивность растворенного вещества в его стандартном состоянии, получим выражение
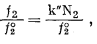 |
(2.31) |
или
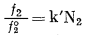 |
(2.32) |
Так как активность любого компонента раствора, согласно определению, всегда равна
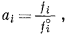 |
(2.18) |
уравнение (2.32) можно переписать следующим образом:
| a2 = k' N2, | (2.33) |
что будет справедливо для бесконечно разбавленного
раствора. Кроме того, поскольку
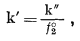 |
(2.34) |
очевидно, что величина k' будет определяться выбранным стандартным состоянием растворенного вещества. Такой выбор зависит от частной задачи, которую следует решить, и в дальнейшем он будет рассматриваться в связи с каждой решаемой проблемой.
Согласно уравнению (2.28), коэффициент активности растворенного вещества определяется выражением
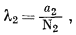 |
(2.28) |
а так как, согласно закону Генри,
| a2 = k' N2 при N2 ® 0, | (2.33) |
то
| l2 = k' при N2 ® 0. | (2.35) |
Из уравнения (2.35) следует, что в бесконечно разбавленном растворе величина l2 не будет отличаться от k'. Этот вывод иллюстрируют Рис. 2.8 и 2.9. Штриховая линия на Рис. 2.8 отражает поведение раствора по закону Генри; степень наклона этой линии, т. е. величина k', равна примерно 3,3. На Рис. 2.9 видно, что lCd при NCd = 0 имеет предельную величину 3,3. При анализе этих фигур следует обратить внимание на то, что по мере приближения NCd к единице поведение раствора все ближе отвечает закону идеального раствора и соответственно lCd также приближается к единице. Можно показать, что для любого раствора, в котором все растворенные вещества подчиняются закону Генри, сам растворитель ведет себя в соответствии с законом идеального раствора.
Практический коэффициент активности. При описании состава раствора в пределах приложимости закона Генри к разбавленным растворам возможно еще одно упрощение. Поскольку для бинарного раствора мольная доля растворенного вещества определяется выражением
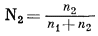
и поскольку при малых значениях n2 справедливо приближенное равенство n1 + n2 @ n1, для разбавленных растворов можно написать выражение
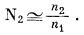 |
(2.36) |
Согласно определению, моляльность раствора m равна числу молей растворенного вещества, приходящихся на 1000 г растворителя,
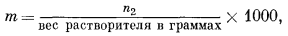
или
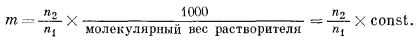 |
(2.37) |
Сопоставив уравнения (2.36) и (2.37), мы увидим, что
| m @ const ґ N2. | (2.28) |
Подставив этот результат в уравнение (2.33), получим
| a2 = km. | (2.39) |
Если закон Генри справедлив при конечных концентрациях растворенного вещества, уравнение (2.39) будет приближенным; в бесконечно разбавленном растворе расчет активностей по уравнениям (2.33) и (2.39) даст одну и ту же величину. Для раствора, содержащего два и более растворенных компонента, приближения, определяемые уравнением (2.39), будут справедливы, и для каждого растворенного компонента i мы можем написать равенство
| ai = kimi. | (2.40) |
Имеет смысл ввести такой коэффициент активности, который относился бы к моляльным концентрациям. Это так называемый практический коэффициент активности gi, определяемый из уравнения
| ai = gimi. | (2.41) |
Величина gi меняется с изменением mi (и в зависимости от температуры и общего давления), а потому уравнение (2.41) справедливо для растворов с любыми концентрациями вне зависимости от того, подчиняются они закону Генри или нет. В случае бесконечно разбавленного раствора, когда растворенное вещество ведет себя в соответствии с законом Генри, gi по величине приближается к ki что хорошо видно при сопоставлении уравнений (2.40) и (2.41).
Минералы, как правило, представляют собой твердые растворы: химический анализ минерала почти всегда обнаруживает отклонения от состава, соответствующего чистому веществу. Так, в родохрозите MnCO3 всегда присутствует растворенный кальций; этот же минерал может содержать закисное железо, магний и цинк. Пределы смесимости компонентов и характер твердого раствора различны и зависят от состава и кристаллической структуры минерала, выступающего в качестве растворителя. Большая часть минералов является солями, т. е. кристаллическими соединениями, построенными из катионов (положительно заряженных ионов) и анионов (отрицательно заряженных ионов). Характерным примером могут служить ранее упомянутый родохрозит, состоящий из ионов Mn2+ и СO2—3, и оливин, состоящий из ионов Mg2+ и SiO4—4. Твердый раствор образуется в результате замещения одного иона в решетке минерала-хозяина другим, подобным ему ионом. Так, Мn2+ в родохрозите может замещаться ионами Са2+ или Fe2+. Если, например, ж грамм-атомов Fe2+ заместили соответствующее количество Мn2+, то формула получившегося твердого раствора будет иметь вид (Fex, Мn1 — x)СО3. Анионы также могут замещать друг друга. Например, молибдат-ион МоO2—4 в некоторых соединениях легко замещает хромат-ион СrO2—4. Возможны и другие, более сложные виды замещения.
Пределы растворимости и устойчивость твердого раствора, образованного вследствие катионного замещения, зависят от того, насколько эти два катиона близки по своим свойствам. Если замещающий катион имеет такой же заряд, как и замещаемый катион, и близкий радиус иона, раствор будет достаточно устойчивым. Так, Fe2+ с ионным радиусом 0,75 А (приложение 3) и Мn2+ с радиусом иона 0,80 А легко замещают друг друга во многих минералах, тогда как Ва2+, например, с радиусом иона 1,35 А не способен замещать Fe2+ и Мn2+.
При повышенных температурах взаимная растворимость минералов значительно возрастает. Это вполне закономерно, если исходить из представлений о кристаллической структуре минералов. С повышением температуры возрастает термальная подвижность каждого иона в решетке и таким образом увеличивается эффективный радиус иона. Поскольку более легкие ионы, обладающие меньшими ионными радиусами, оказываются относительно более подвижными, величины эффективных ионных радиусов всех элементов с повышением температуры все более сближаются. Например, ион К+ (rK+ = 1,33 А), замещает Na+ (rNa+ = 0,95 А) в NaCI при 25° С лишь в незначительной степени, но при температуре свыше 500° КС1 и NaCI образуют гомогенный твердый раствор в любых пропорциях.
Важно отметить, что опубликованные данные химических анализов многих минералов соответствуют твердым растворам, термодинамически неустойчивым при комнатной температуре. Как указывалось выше, растворимость сильно увеличивается с повышением температуры; когда же минеральный раствор, образованный при повышенных температурах, остывает, низкая скорость реакции распада раствора зачастую приводит к тому, что система не достигает равновесия. Итак, при термохимических построениях следует учитывать, что минералы обычно представляют собой неустойчивые системы.
Согласно определению, активность чистого твердого вещества при давлении 1 атм и при данной температуре равна единице. Однако в случае твердого раствора при тех же условиях активность кристаллического растворителя, как правило, отличается от единицы. Таким образом, aMnCo3 в (Fе0,2Мn0,8)СО3 не равна единице. Если твердый раствор идеален, для него справедливо уравнение (2.21), т. е.
ai = Ni.
Так, для приведенного выше случая при условии, что МnСО3 ведет себя идеально в пределах состава, близкого к (Fе0,2Мn0,8)СО3 (точно мы этого не знаем), активность МnСО3 определяется следующим уравнением:
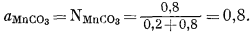
Во всех случаях справедливо уравнение (2.28), согласно которому
ai = li Ni.
Р е г у л я р н ы й р а с т в о р. В достаточно приближенном виде поведение многих бинарных растворов неэлектролитов описывается уравнением
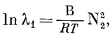 |
(2.42) |
в котором В-константа, не зависящая от состава. Уравнение (2.42) можно написать следующим образом:
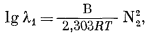 |
(2.43a) |
или
| ln l1 = B' N22 = B' ( l - N1 )2. | (2.43б) |
Растворы, для которых справедливо уравнение (2.42), называются регулярными1 (стр.48).
Уравнение (2.43б) показывает, что с приближением Ni к единице li приближается к единице, а следовательно, и аi также стремится к единице. Такой вывод соответствует условию, согласно которому за стандартное состояние компонента i принят этот компонент в виде чистого вещества. Поэтому подразумевается, что уравнение регулярного раствора относится к тем случаям, когда стандартным состоянием компонентов бинарного раствора являются чистые вещества.
Величины ln l и N в уравнении (2.43а) безразмерные; следовательно, В будет иметь ту же размерность, что и RТ. Если R выразить в ккал/градґмоль, то В будет выражаться в ккал/градґмольґград = ккал/моль. При 298,15° К (25° С) уравнение (2.43а) примет вид
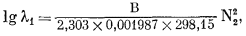 |
(2.43в) |
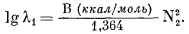 | |
О поведении твердых
растворов и расплавов, представляющих геологический интерес, известно еще
сравнительно мало, но скорее всего они
|
1 (стр.48) Используемый здесь термин "регулярный раствор" имеет лишь то значение, которое вкладывается в него в настоящей работе, и не является универсальным понятием. Вместо этого термина некоторые авторы применяют выражение "симметричный раствор" (см., например, [9]). |
близки к регулярным растворам. Установлено, что для большинства систем, важных для геологов, значение константы В' колеблется в пределах от нуля (идеальный раствор) до ±5 (Стефенсон, Массачусетский технологический институт, личное сообщение).
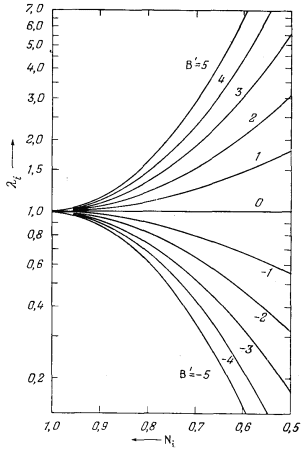 |
| Рис. 2.11. Зависимость коэффициента активности li (в логарифмической шкале) от мольной доли Ni; дана в виде фiункции lg li = В' (1 - Ni)2 при значениях В' от -5 до +5. |
На Рис. 2.11 приведен пучок кривых, иллюстрирующих зависимость коэффициента активности li от мольной доли Ni для компонента i бинарного раствора при значениях В' от -5 до +5. Анализ Рис. 2.11 позволяет сделать важный вывод: при любых учтенных значениях В' коэффициент активности стремится к единице по мере того, как мольная доля приближается к единице. Следовательно, можно считать, что даже для растворов, поведение которых в широком диапазоне концентраций значительно отличается от идеального, растворитель ведет себя идеально, как только раствор становится разбавленным. В частности, без большой ошибки можно полагать, что минерал, содержащий небольшую примесь другого компонента, ведет себя идеально.
Наши представления о поведении растворенного вещества, т. е. подчиненного компонента раствора, значительно менее определенны. Из Рис. 2.11 явствует, что с уменьшением Ni значения li при данном Ni все больше и больше зависят от принятой величины В'. Суммируя все изложенное, можно с достаточной осторожностью предположить, что компонент раствора, мольная доля которого Ni і 0,9, будет вести себя идеально. Поскольку мы не знаем точной величины В' (входящей в определение регулярного раствора), мы не можем прийти к каким-либо выводам, касающимся поведения компонента i при Ni < 0,9.
Н е к о т о р ы е э к с п е р и м е н т а л ь н ы е д а н н ы е о т н о с и т е л ь н о р е г у л я р н ы х р а с т в о р о в. Солстром и Хилдебранд [26—28] на основании данных, полученных при исследовании активности бромида серебра в растворе расплавленных бромидов лития, натрия, калия и рубидия при 500-600° С, показали, что каждая такая система в общем близка к регулярному раствору. На Рис. 2.12 приведены результаты, полученные этими авторами для AgBr, растворенного в LiBr, и AgBr, растворенного в КВr, при 550° С. На этом графике нанесены значения lg lAgBr в зависимости от (1 — NAgBr)2 в соответствии с уравнением (2.43б). Поскольку для каждого из двух растворов точки лежат на прямой с наклоном, отвечающим В', можно считать эти растворы регулярными. Приведенные данные свидетельствуют о том, что эти растворы действительно близки к регулярным. Для AgBr, растворенного в LiBr, константа В' из уравнения (2.43б) приблизительно равна 0,50, а для AgBr, растворенного в КВr, В' составляет примерно — 0,38.
Экспериментально исследованы и некоторые другие пары солей и сплавы; при этом также установлено, что они ведут себя как регулярные растворы, по крайней мере приблизительно. Полученные результаты, в частности, рассмотрены в гл. 10 работы Даркена и Гэрри [З].
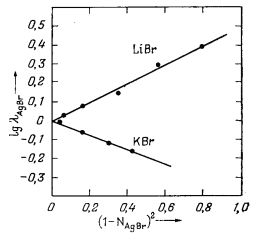 |
| Рис. 2.12. Зависимость lg lAgBr от величины (1 — NAgBr)2 для AgBr, растворенного в LiBr и КВг; температура 550° С [28]. |
П о п р а в к и к в е л и ч и н е а к т и в н о с т и т в е р д ы х в е щ е с т в, в в о д и м ы е в с в я з и с к о л е б а н и я м и с о с т а в а. Минералы обычно не представляют собой чистых веществ, и это следует принимать во внимание при термохимических расчетах, касающихся активности минералов. В настоящее время в связи с невозможностью оценки отклонения поведения твердых растворов от идеального методика таких расчетов основывается на предположении об идеальном поведении и оценке того предела концентрации, до которого подобное предположение будет справедливо.
При проведении расчетов возникает следующий вопрос. Имеются, скажем, необходимые термохимические данные для вычисления равновесного произведения активностей кальция и карбонат-ионов в водном растворе, находящемся в равновесии с чистым кальцитом. Насколько изменится это произведение, если кальцит содержит 5 мол. % MgCO3? Чтобы ответить на этот вопрос, прежде всего необходимо определить константу равновесия для случая диссоциации кальцита при 25° С и 1 атм общего давления. В таких условиях для реакции
CaCO3 кальцит = Ca2+водн
+ CO2—3 водн,
DF°реакции = DF°обр Ca2+ + DF°обр CO2—3 —
DF°обр
CaCO3,
11,38 ккал = — 132,18 + (—126,22) —
(—269,78).
Поскольку из уравнения (1.12) следует, что
DF°реакции = —1,364 lg K
то
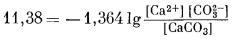
и
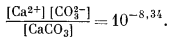 |
(2.44) |
Для чистого кальцита [СаСО3] равна единице, а поэтому произведение активностей ионов равно 10—8,34. Но какова же будет активность СаСО3 в соединении (Са0,95Мn0,05)СО3? Исходя из предположения об идеальном поведении раствора,
[СаСО3] = NCaCO3 = 0,95.
Подставив этот результат в уравнение (2.44), находим
[Са2+] [СО2—3] = 10—8,34 ґ 0,95 = 10—8,36.
Если (Са,Мn)СО3 не представляет собой идеальный раствор, но предположительно является регулярным раствором, то, согласно Рис. 2.11, lCaCO3 лежит в пределах от 0,98 до 1,02 (при всех возможных значениях В' от максимального до минимального). Следовательно, активность СаСО3, рассчитанная по уравнению (2.28), будет находиться где-то между следующими двумя значениями:
[СаСО3] = lСаСО3
NСаCО3,
0,93 = 0,98 ґ
0,95,
0,97 = 1,02 ґ 0,95.
В табл. 2.3 приведены произведения активностей ионов кальция и карбонат-ионов, равновесных по отношению к (СаМn)СО3; эти результаты основаны на трех различных предположениях.
Таблица 2.3
| Твердая фаза | СаСО3 | [Са2+] [СO2—3] |
| Чистый кальцит | 1 | 10—8,34 |
| (Са0,95Мn0,05)СО3 | 0,95 (идеальный раствор) |
10—8,36 |
| (Са0,95Мn0,05)СО3 | 0,97 (В' = +5) | 10—8,35 |
| (Са0,95Мn0,05)СО3 | 0,93 (В' = —5) | 10—8,37 |
Что касается растворенного компонента, то никаких выводов относительно его активности сделать нельзя. Для рассмотренного случая активность МnСО3 в соединении (Са0,95Мn0,05)СО3 необходимо установить экспериментально.
Изучение фазовых равновесии показывает, что во многих природных системах растворимость веществ в твердом состоянии ограничена. Состав тех соединений, с которыми нам приходится иметь дело, никогда значительно не отклоняется от состава чистого вещества, что позволяет, как было показано выше, достаточно точно оценить активность главных компонентов (растворителей). При более широкой или даже полной взаимной растворимости единственная возможность опять-таки заключается в предположении (разумеется, при отсутствии доказательств обратного) идеального поведения главного компонента для состава, близкого к чистому веществу. Пример тому можно видеть в ранее рассмотренных расплавленных парах солей AgBr — LiBr и AgBr — КВr, характеризующихся неограниченной смесимостью. Было показано, что в этих системах (Рис. 2.12) lAgBr близок к единице только тогда, когда NAgBr приближается к единице, а при всех прочих вариациях состава растворы ведут себя согласно теории регулярных растворов с В', существенно отличающимся от нуля.
Величину коэффициентов активности можно получить, используя данные по равновесным составам. Так, например, известно [25], что при 25° С равновесный состав кальцита и сидерита соответственно определяется соединениями примерного состава (Сa0,95Fe0,05)СО3 и (Fe0,95Ca0,05)CO3. Когда эти две фазы находятся в равновесии, активность СаСО3 в кальците должна быть равна активности СаСО3 в сидерите (за стандартное состояние принят чистый кальцит при 1 атм общего давления и температуре, реальной для обеих фаз). Итак,
aCaCO3(кальцит) = aCaCO3(сидерит).
Поскольку кальцит представляет собой почти чистое вещество,
aCaCO3(кальцит) = a' = l' N' @ 1 ґ 1 @ 1.
Следовательно,
aCaCO3(сидерит) = a" = l" N" @ 1.
а так как
N" = 0,05,
то
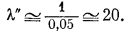
Если для других веществ будут получены такие же данные, как для кальцита и сидерита, то путем подобных вычислений для них также можно будет определить коэффициенты активности.
Для геологов весьма полезны соотношения, выведенные химиками для растворов неэлектролитов; с их помощью можно описать широкий круг явлений растворения в природных системах, в том числе процессы, происходящие в магмах, твердые растворы в минералах, явления катионного обмена и поведение природных органических веществ. Среди ключевых закономерностей отметим закон Рауля Рi = P*iNi, который можно непосредственно применять к системам, содержащим летучий компонент, и который, что очень важно, подводит к понятиям фугитивности fi и активности ai. Вывод соотношения между фугитивностью и активностью компонента позволяет рассчитать активность летучего компонента в водных и других средах, исходя из результатов измерения его фугитивности. Закон Генри f2 = k"N2 описывает поведение растворенного вещества во всех растворах неэлектролитов с конечной степенью разбавления. Для неидеального раствора при любой концентрации веществ вводится понятие коэффициента активности li, который связывает активность с мольной долей (аi = liNi). Установлено, что многие бинарные системы, в том числе минералы, представляют собой "регулярные" растворы; другими словами, коэффициент активности каждого компонента определяется уравнением типа lg l1 = В(1 — N1)2. Расчеты, приведенные в качестве примера, демонстрируют целесообразность применения теории неэлектролитов при решении ряда типичных проблем
Раствором электролита называется такой раствор, в котором растворенное вещество частично или полностью находится в виде ионов. При дальнейшем изложении в качестве растворителя будет рассматриваться жидкая вода1 (стр.52) , но с соответствующими поправками все выводы можно отнести к любому другому растворителю.
Действительная природа
растворенного вещества в водном растворе с точки зрения кинетики
чрезвычайно сложна; она зависит от особенностей
|
1 (стр.52) В глубинных геологических процессах существенную роль, вероятно, играют и другие растворители, например флюиды, состоящие из углекислоты, аммония или сероводорода; однако данные относительно их ионизирующей способности явно недостаточны. |
растворенного вещества, концентрации раствора, а также от наличия или отсутствия других химических компонентов. Для удобства изложения материала разделим электролиты на два класса: неассоциированные (диссоциированные) электролиты и ассоциированные электролиты1 (стр.53) .
Под неассоциированным электролитом подразумевается такое растворенное вещество, которое находится в растворе исключительно в форме простых катионов и анионов (возможно, лишь гидратированных). Неассоциированными, или сильными, электролитами считаются такие соли, как NaCl и КСl. Однако, как указывают Робинсон и Стокс 124], "главным критерием, определяющим отнесение электролита к данному классу, служит отсутствие убедительных доказательств какой-либо формы ассоциации".
Ассоциированные электролиты делятся на два класса: слабые электролиты и ионные пары. Слабым электролитом считается такое растворенное вещество, которое может существовать как в виде недиссоциированных ковалентных молекул, так и в форме ионов. В этот класс попадают кислоты, некоторые основания и совсем немногие неорганические соли. В растворе углекислоты, например, наряду с ионами НСО—3 и СO2—3 содержатся недиссоциированные молекулы Н2СО3; в концентрированных растворах соляной кислоты вместе с ионами Н+ и С1— находится значительная доля молекул НСl.
Термин "образование ионных пар" относится к формированию ассоциации противоположно заряженных ионов в результате одного лишь электростатического взаимодействия, причем в ходе этого процесса не образуются ковалентные связи (электронные пары), как это имеет место в случае слабых электролитов. Например, в растворах сульфата кальция, как и в растворах сульфата других двухвалентных металлов, основная масса ионов Са2+ и SO2—4 ассоциирует с образованием нейтральных частиц CaSO°4; в растворах гидроокиси кальция некоторая часть растворенного вещества также находится в форме ионной пары Са(ОН)+.
Не всегда можно решить, как следует называть данный растворенный компонент, безусловно относящийся к ассоциированным электролитам: слабым электролитом или ионной парой. Поэтому такое разграничение скорее проводится для удобства.
Термин "комплексные ионы" используется для обозначения всех ионов, состоящих более чем из одного атома. Так, Са(ОН)+, СO2—3, HCO—3, HS—, ZnCl2—4 и B3О3(ОН)—4 - все это комплексные ионы; здесь нет нужды останавливаться на природе межатомных сил связи.
Следует подчеркнуть, что конкретное состояние растворенного вещества в значительной степени зависит от концентрации раствора. С увеличением концентрации частицы растворенного вещества в среднем сближаются и все сильнее взаимодействуют друг с другом, образуя ковалентные или электростатические связи. Так, повышенные концентрации благоприятны для формирования нейтральных молекул или комплексных ионов. При разбавлении раствора, напротив, происходит разъединение сложных частиц на простые гидратированные ионы.
Установлено, что активность
растворенного электролита подчиняется закону Генри, если при этом
учитывается степень диссоциации электролита. Для одно-одновалентных
растворенных веществ типа соляной кислоты НСl, которая диссоциирует на
ионы Н+ и Сl—, в формулу закона Генри вво-
|
1 (стр.53) Данные о неассоциированных и ассоциированных электролитах изложены в соответствии с работой Робинсона и Стокса [24, гл. З]. |
дится квадрат моляльности. В области бесконечных разбавлении закон Генри приобретает следующую форму:
| a2 = km22. | (2.45) |
Выражение (2.45) справедливо для всех одно-одновалентных растворенных электролитов, таких, как NaCl и LiF, а также для всех симметричных солей, в которых анион и катион обладают одинаковой валентностью,
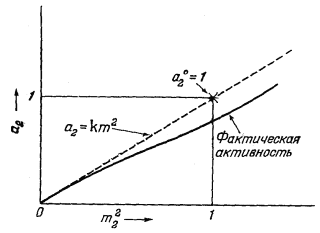 |
| Рис. 2.13. Диаграмма активность — моляльность для раствора
симметричного электролита при данных температуре, и
давлении. Диаграмма построена следующим образом: измеренные величины активности наносились в произвольном числовом масштабе относительно m22; они показаны сплошной линией. Таким путем установлен предельный наклон этой пинии при m22, стремящейся к нулю, который обозначен штриховой линией и соответствует уравнению а2 = km22. Звездочка, проставленная на штриховой линии при m22 = 1, отвечает стандартному состоянию растворенного вещества, когда а2 = a°2 = 1. Тем самым определен численный масштаб активности. В зависимости от выбранного стандартного состояния мы имеем k = 1 и, следовательно, а2 = m22 как предельное соотношение. |
например MgSO4 и CaCO3. В случае тройной соли типа BaCl2, каждый моль которой диссоциирует на 3 моль ионов, закон Генри выражается по-иному:
| a2 = km32. | (2.46) |
В общем для электролита, диссоциирующего на ионы по схеме n = n+ + n—, согласно уравнению
Cn+An— = n+ C + n—A,
в котором С — катион (с соответствующим зарядом), а А — анион, закон Генри выражается следующим образом:
| a2 = kmn2. | (2.47) |
С и м м е т р и ч н ы е э л е к т р о л и т ы. Величина константы пропорциональности k зависит от выбранного стандартного состояния растворенного вещества. Для электролита за стандартное состояние чистое твердое вещество или жидкость не принимаются. В случае симметричного соединения, для которого справедливо уравнение (2.45), стандартное состояние подбирается таким образом, как это иллюстрирует Рис. 2.13. Как будет показано, стандартное состояние - это некоторое гипотетическое состояние, определяемое поведением раствора при бесконечном разбавлении; согласно такому выбору, стандартное состояние симметричного электролита выражается следующим образом:
| a2 = m22 при m ® 0. | (2.48) |
Как только раствор становится бесконечно разбавленным, взаимодействие между катионами и анионами прекращается. В случае симметричного электролита мы вправе предположить, что моляльность катионов и анионов будет одинакова и равна моляльности растворенного вещества, т. е.
| m2 = m+ = m—. | (2.49) |
Подставляя это равенство в уравнение (2.48), получим
| a2 = (m2)(m—). | (2.50) |
Активности индивидуального иона для катионов и анионов обозначаются соответственно как а+ и а—; определяются они следующим образом:
| a+ = m+ при m2 ® 0, | (2.51a) |
| a— = m— при m2 ® 0. | (2.51б) |
Поскольку в бесконечно разбавленном растворе m+ = m—, то в этих условиях a+ = а—.
Подставив равенства (2.51а) и (2.51б) в уравнение (2.50), получим
| a2 = (a+)(a—). | (2.52) |
Несмотря на то что уравнение (2.52) выведено для бесконечно разбавленного раствора, оно отражает важные соотношения для всех концентраций и, таким образом, принимается за определяющее для всех концентраций.
Средняя ионная активность симметричного электролита a+ равна
| a+ = (a+a—)1/2 = a1/2. | (2.53) |
Коэффициенты, активности индивидуального иона определяются выражениями
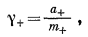 |
(2.54a) |
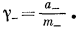 |
(2.54б) |
Поскольку при бесконечном разбавлении с приближением m+ и m— к нулю отношения а+/m+ и a—/m— становятся равными единице, то g+ и g— при бесконечном разбавлении тоже приближаются к единице.
Коэффициент средней ионной активности определяется как
| g± = (g+g— )1/2. | (2.55) |
Согласно уравнениям (2.54а) и (2.54б),
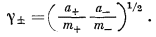 |
(2.56) |
Как следует из уравнения (2.53), (а+а—)1/2 = а+ = а1/22. Если за среднюю ионную моляльность симметричного электролита мы примем
| m± = (m+m— )1/2. | (2.57) |
и сохраним формальное соотношение m2 = m+ = m— для всех концентраций, то получим
m± = m2;
таким образом, уравнение (2.56) сводится к выражению
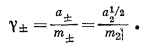 |
(2.58) |
Так как, согласно уравнению (2.48), отношение а1/22/m2 приближается к единице по мере приближения m2 к нулю, то g+ при бесконечном разбавлении также будет стремиться к единице.
Н е с и м м е т р и ч н ы е э л е к т р о л и т ы. Соотношения между активностью и концентрацией несимметричного электролита можно вывести таким же путем, как и для симметричного электролита. Для электролита Сn+Аn—, который диссоциирует на n+ положительных ионов и n— отрицательных, закон Генри выражается следующим образом:
| a2 = km2(n+ + n— ) = kmn2. | (2.59) |
Активность индивидуального иона связана с активностью растворенного вещества а2 соотношением
| a2 = (a+)n+ (a— )n—. | (2.60) |
Средняя активность а+ равна
| a± = [(a+)n+ (a— )n—]1/n, | (2.61) |
средняя ионная моляльность m± составляет
| m± = m2[(n+)n+ (n— )n—]1/n, | (2.62) |
а средний коэффициент активности g± равен
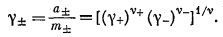 |
(2.63) |
Таким образом, для общего случая коэффициент активности g+ в бесконечно разбавленном растворе близок к единице. Уравнения (2.54а) и (2.54б), характеризующие коэффициенты активности индивидуального иона для симметричного электролита, справедливы и для общего случая.
Хотя коэффициенты
активности индивидуального иона нельзя измерить непосредственно,
коэффициенты средней ионной активности можно определить с достаточной
степенью точности. Для этих целей разработаны многие методы; в учебной
химической литературе приведен необходимый справочный материал для
широкого диапазона концентрации [12, гл. 21; 13, стр. 349-358; 8; 24,
приложения; 20; I]. Исходя из измеренных коэффициентов средней ионной
активности, с помощью различных методов можно вывести полуэмпирические
значения коэффициентов активности индивидуальных ионов,
Прежде чем изложить методику определения коэффициентов активности индивидуального иона, необходимо рассмотреть важнейшую часть такого определения, а именно расчет растворимости.
Геологу нужно научиться рассчитывать растворимость веществ в различных водных средах. Для этого необходимо знать зависимость между активностью растворенных частиц (компонентов) данного элемента и общей концентрацией элемента, определяемой путем химического анализа.
Прежде всего следует отметить, что расчет растворимости до сих пор представляет собой скорее искусство, чем научный метод, и что сомнительно всякое значение растворимости, определенное лишь теоретически. Растворимость данного элемента - это сумма стехиометрических концентраций всех находящихся в растворе компонентов, которые содержат данный элемент. Таким образом, точный подсчет растворимости требует выявления всех комнонентов раствора, определяющих результат химического анализа, а также соотношения между концентрацией данных компонентов и их активностью.
Поэтому при расчете растворимости геохимик должен обстоятельно знать химию рассматриваемого им элемента; однако и при таком условии достоверность полученного результата должна быть подтверждена экспериментальным путем. Все же в ряде случаев имеется возможность вычислить минимальную растворимость, знание которой при решении геохимических вопросов почти столь же полезно, как и истинной растворимости.
Концентрация данного элемента в водном растворе, определенная с помощью количественного анализа, может быть выражена следующим равенством:
| mA = еms, | (2.64) |
где mA - валовая моляльность, определяемая соотношением
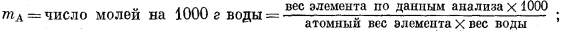
ms - сумма моляльностей всех компонентов раствора, содержащих данный элемент; в этом случае моляльность каждого данного компонента устанавливается с помощью того же выражения, что и величина mA, однако допускается, что этот компонент может быть выделен и определен количественно.
Чтобы ввести значение mA в подсчеты активности индивидуального компонента, необходимо установить зависимость между активностью и моляльностью. Итак,
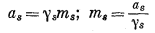 |
(2.65) |
и
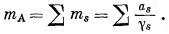 |
(2.66) |
Допустим, например, что вода насыщена углекислотой при данном парциальном давлении и что количество растворенного вещества определено по потере веса углекислого газа в питающем резервуаре. Тогда
mA(CO2) = еms.
В нашем случае, как известно из химии, главные растворенные компоненты представлены H2CO3, НСО—3 и СO2—3. Поэтому
mA(CO2) = mCO2 водн + mH2CO3 + mHCO—3 + mCO3 + mx + my + ...
Члены mx, my и т. д. использованы для обозначения тех компонентов, присутствие которых в подобном растворе к настоящему времени с достоверностью не установлено. Таким образом, если рассматривать только СO2 водн, H2CO3, HCO—3 и СO2—3, то величина mA (CO2) полученная путем их сложения, будет меньше величины, определенной аналитически, на сумму моляльностей этих неизвестных. Когда такая сумма незначительна или близка к ошибке анализа, приближенное выражение
| mA(CO2) = mCO2 водн + mH2CO3 + mHCO—3 + mCO2—3 | (2.67) |
удовлетворительно; во всяком случае, величина mA (CO2) не будет меньше суммы моляльностей неизвестных компонентов.
Если мы захотим рассчитать mA(CO2) на основании термохимических соотношений, то, зная данное парциальное давление СО2, вычислим значение аCO2 водн, аH2СО3, aHCO—3 и aCO2—3. Если к тому же нам известны значения gCO2 водн, gH2СО3, gHCO—3 и gCO2—3, то мы вправе написать
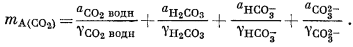 |
(2.68) |
Это приближенное равенство так же ограничено, как и уравнение (2.67). Кроме того, при определении ряда входящих в него параметров, в частности активностей и коэффициентов активности, может возникнуть ряд неточностей. Итак, приближенное значение растворимости данного элемента может быть получено посредством термохимических расчетов, но только в том случае, если имеются подробные сведения относительно всех растворенных компонентов, определяющих растворимость данного элемента, и если могут быть получены точные значения их коэффициентов активности. Если же какая-то часть перечисленных величин остается неизвестной, рассчитанные значения растворимости будут меньше тех, которые определяются из опыта1 (стр. 58); иногда разница весьма значительна.
Понятие об ионной силе, которое предложено Люисом и Рендаллом [14; 15, гл. 28], вскрывает чрезвычайно полезную закономерность, позволяющую оценить влияние активности нескольких электролитов на данный электролит в общем растворе. Выражаясь словами этих авторов, "для случая разбавленных растворов коэффициент активности данного сильного электролита равен коэффициенту активности этого электролита во всех растворах с той же ионной силой" [15]. Ионная сила I равна
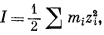 |
(2.69) |
в котором mi - моляльность, a zi - заряд иона i в данном растворе; суммируются все ионы, положительные и отрицательные. Например, ионная сила 1-моляльного раствора CaCl2 равна
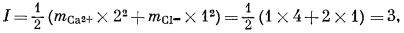
а тот же показатель для 1-моляльного раствора NaCl составит
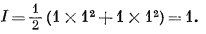
Ионную силу природных вод можно рассчитывать на основании данных химического анализа, поскольку эти данные выражаются в концентрации либо главных ионов, либо растворенных солей.
В табл. 2.4 приводятся результаты анализа вод, взятых в районе нефтеносного поля Кат-Бэнк в Монтане из так называемого медисонского песчаника миссисипского (нижнекаменноугольного. — Ред.) возраста [2, стр. 193].
Таблица 2.4
| Na+ | Са+ | Mg+ | SO2—4 | Cl— | СO2—3 | HCO—3 |
| 2187 | 39 | 57 | 232 | 1680 | 84 | 2850 |
|
1 (стр.58) В сильно концентрированных растворах величина as иногда превышает величину ms и подсчитанная растворимость может превышать наблюдаемую. Это явление редко встречается в растворах с концентрацией, меньшей 1 моль на 1 л. |
Прежде всего следует перевести результаты анализа, выраженные в миллионных долях, в моляльность (табл. 2.5), пользуясь уравнением1 (стр. 59);
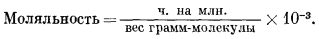
Таблица 2.5
| Nа+ | Са+ | Мg+ | SO2—4 | Сl— | СO2—3 | НСО—3 |
| 0,0951 | 0,00097 | 0,0023 | 0,00242 | 0,0474 | 0,0014 | 0,0467 |
Взяв значения моляльности для ионов в том порядке, как они помещены в таблицах, получим
I = 1/2 (0,0951 ґ
12 + 0,00097 ґ 22 + 0,0023
ґ 22 + 0,0024 ґ 22 +
+ 0,0474 ґ 12 + 0,0014 ґ
22 + 0,0467 ґ 12) = 0,109.
Вычисленное значение близко к средней величине ионной силы для вод, циркулирующих в горных породах. В речных и озерных водах эта величина уменьшается примерно в 10 раз, а в океане, напротив, она приблизительно в 10 раз выше.
Понятие ионной силы полезно при сравнении растворов различного состава, так как позволяет учесть электростатическое взаимодействие разноименных ионов. Поскольку электростатическое взаимодействие ионов представляет собой функцию квадрата их заряда, ионная сила является более полезным критерием поведения раствора, чем его концентрация. Хотя ионную силу нельзя рассматривать как панацею от всех бед, однако с ее помощью можно избежать ошибок, связанных с игнорированием частного взаимодействия между составными частями раствора. При определении ионной силы, так же как и при определении растворимости, приходится прибегать к ряду допущений. При расчете ионной силы мы должны знать главные ионы, присутствующие в растворе. Как и в предыдущем примере, прежде всего следует учесть главные растворенные компоненты. Если путем теоретических или экспериментальных исследований установлено присутствие и других компонентов, их также нужно ввести в расчет значения ионной силы. В общем главные компоненты природных вод достаточно хорошо известны, так что значения ионной силы, вычисленные по тому составу ионов, который дается обычными химическими анализами, мало чем отличается от значения ионной силы, получаемого при более детальных исследованиях.
Несомненно, например, что вода из медисонского песчаника содержит следы бора и йода, а также небольшие количества калия. Но если и учесть сумму этих компонентов, то значение ионной силы изменится не больше чем на 1—2%.
На Рис. 2.14 представлены
типичные кривые, отражающие зависимость между экспериментально измеряемыми
средними коэффициентами активности и ионной силой. Эта диаграмма
показывает влияние валентности
|
1 (стр.59) Здесь следовало бы ввести поправку, поскольку данные анализа выражены в граммах па 106 г раствора, а не в граммах на 106 г H2О. Однако получающаяся ошибка очень мала. |
на величину коэффициента активности. Так, одно-одновалентная соль КСl имеет наибольшую величину коэффициента активности; для солей Nа2SO4
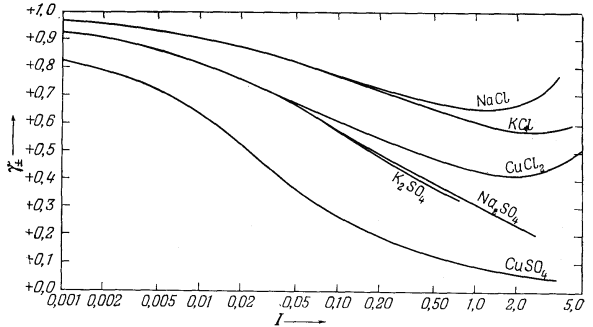 |
| Рис. 2.14. Зависимость средних коэффициентов
активности некоторых типичных солей от ионной силы раствора (шкала
логарифмическая). Обратите внимание на поведение солей одинакового типа валентности при ионной силе, меньшей 0,1 [13]. |
и СuСl2, представляющих собой соединения двухвалентного иона с двумя одновалентными, кривые совпадают до значения ионной силы 0,1; двух-двухвалентная соль СuSO4 характеризуется наименьшим коэффициентом активности.
Как мы уже упоминали, существует возможность точного экспериментального определения коэффициентов средней ионной активности, однако коэффициент активности индивидуального иона непосредственно измерить нельзя. Это затруднение можно обойти, допустив, что для стандартного одно-одновалентного электролита g+ = g— в условиях интересующих нас значений ионной силы. Основой расчета коэффициентов активности индивидуального иона служит поведение КСl в растворе [15]. Различными способами доказано, что в этом случае gK+ и gCl— имеют одинаковые значения1 (стр. 60); . Отсюда мы можем вывести приближенное равенство
| g±КСl = [(gК+) (gCl-)]1/2 = gK+ = gСl- | (2.70) |
Используя это соотношение, по имеющимся коэффициентам средней ионной активности можно составить таблицу значений коэффициентов активности индивидуальных ионов.
Так, для одновалентного хлорида
| g±MСl = [(gM+) (gCl-)]1/2 = [(gM+) (g±KСl)]1/2, | |
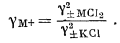 |
(2.71) |
|
1 (стр.60) Допущение о равенстве gK+ и gCl— в чистом растворе КСl было предложено Макиннесом [17], поэтому оно часто называется допущением Макиннеса. |
| g±MСl2 = [(gM2+) (gCl-)2]1/3 = [(gM2+) (g±KСl)2]1/3, | |
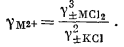 |
(2.72) |
Для прочих солей калия можно использовать обратную зависимость и получить коэффициенты активности анионов. Например,
| g±K2SO4 = [(gK+)2 (gSO2—4)]1/3 = [(g±KCl)2 (gSO2—4)]1/3, | |
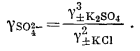 |
(2.72) |
Чтобы определить gCu2+ для солей типа СuSO4, необходим более сложный расчет. Сначала составим уравнение
| g±СuSO4 = [(gСu2+) (gSO2—4)]1/2, | (2.74) |
а затем, подставив значение gSO2—4 полученное из уравнения (2.73), и сделав соответствующие преобразования, найдем
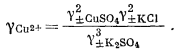 |
(2.75) |
В дальнейшем мы будем называть этот способ вычисления коэффициентов активности индивидуального иона по коэффициентам средней активности среднесолевым методом (mean salt method).
Ошибки, связанные с применением этого метода, трудно поддаются оценке; во всяком случае, они становятся больше при увеличении числа вспомогательных уравнений. Наилучшая проверка всегда заключается в эксперименте. Так, серия коэффициентов активности индивидуального нона будет иметь ценность в том случае, если каждый из них в комбинации с коэффициентами активности других ионов будет соответствовать среднему коэффициенту активности, согласующемуся с экспериментальным определением. Поскольку средний коэффициент активности электролита находится в функциональной зависимости от ионной силы, коэффициент активности индивидуального иона также будет зависеть от ионной силы. Рассматривая разбавленные растворы смешанных электролитов, мы исходим из допущения, что коэффициент активности данного иона зависит только от ионной силы.
Даже в самых разбавленных растворах электролитов заряженные ионы испытывают электростатическое взаимодействие, что сказывается на понижении величины коэффициента активности. Это явление с количественной стороны объясняется теорией Дебая - Хюккеля и несколькими следующими из нее уравнениями, что имеет огромное значение для обработки экспериментальных данных [12, стр. 328-336; 16, гл. 23]. Два таких уравнения мы рассмотрим ниже.
Уравнение Дебая - Хюккеля, определяющее коэффициент активности индивидуального иона в разбавленных растворах, выглядит следующим образом:
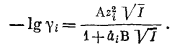 |
(2.76) |
Значения zi и I этого уравнения только что были указаны при определении понятия ионной силы; А и В - характеристические константы растворителя (в данной работе рассматривается только вода) при данных температуре и давлении. В табл. 2.6 приведены значения А и В как функции температуры
Таблица 2.6
| Температура, °С | А | В (ґ I0—8) | Температура, °С | А | В (ґ I0—8) |
| 0 | 0,4883 | 0,3241 | 35 | 0,5175 | 0,3297 |
| 5 | 0,4921 | 0,3249 | 40 | 0,5221 | 0,3305 |
| 10 | 0,4960 | 0,3258 | 45 | 0,5271 | 0,3314 |
| 15 | 0,5000 | 0,3262 | 50 | 0,5319 | 0,3321 |
| 20 | 0,5042 | 0,3273 | 55 | 0,5371 | 0,3329 |
| 25 | 0,5085 | 0,3281 | 60 | 0,5425 | 0,3338 |
| 30 | 0,5130 | 0,3290 |
(при давлении 1 атм). Величина множителя а°i зависит от "эффективного диаметра" данного иона в растворе и преимущественно определяется экспериментальным путем. Список значений а°i (для разных ионов) приведен в табл. 2.7. Физический смысл величины а°i которая обычно связывается
Таблица 2.7
| а°i ґ 108 | Ионы |
| 2,5 | Rb+, Cs+, NH+4 T1+, Ag+ |
| 3,0 | K+, Cl—, Br—, I—, NO—3 |
| 3,5 | OH—, F—, HS—, ВrО—3, IO—4 МnО—4 |
| 4,0—4,5 | Na+, НСО—3, H2PO—4, НSO—3, Hg2+2, SO2—4, SeO2—4, CrO2—4, HPO2—4, PO3—4 |
| 4,5 | Pb2+, CO2—3, SO2—3, MoO2—4 |
| 5,0 | Sr2+, Ba2+, Ra2+, Cd2+, Hg2+, S2—, WO2—4 |
| 6 | Li+, Ca2+, Cu2+, Zn2+, Sn2+, Mn2+, Fe2+, Ni2+, Co2+ |
| 8 | Mg2+, Be2+, |
| 9 | H+, Al3+, Сr3+, трехвалентные редкие земли |
| 11 | Th4+, Zr4+, Ce4+, Sn4+ |
с диаметром данного иона в растворе, заслуживает краткого разъяснения. Значения как правило, превышают а°i величину ионных диаметров, установленную для ионов в кристаллах. Вероятно, эта разница возникает за счет оболочки из молекул воды, которые окружают данный ион в растворе. Были предприняты попытки структурной интерпретации величины а°i, однако четкого представления относительно координации молекул воды вокруг заряженных ионов до сих пор не выработано. Подробно о проблеме гидратации см. в работе Робинсона и Стокса [23].
Наилучшим методом определения активности индивидуального иона в растворах с ионной силой, превышающей 0,05, считается среднесолевой метод. В растворах с меньшей ионной силой среднесолевой метод и расчеты по уравнению (2.76) обычно дают сходные результаты; с помощью уравнения Дебая - Хюккеля, кроме того, можно проводить экстраполяцию в область бесконечного разбавления. Если величина ионной силы становится очень низкой, уравнение (2.76) сокращается до следующего предельного выражения:
| —lg gi = Az2iЦ`I. | (2.77) |
То же выражение для среднего коэффициента активности электролита, образованного лишь двумя различными ионами, в предельном случае бесконечно разбавленного раствора выглядит следующим образом:
| —lg g± = A|z+z—|Ц`I. | (2.78) |
(символ | | обозначает абсолютную величину).
На Рис. 2.15 приведены значения коэффициентов активности индивидуального иона для некоторых обычных ионов, определенные среднесолевым методом и вычисленные по уравнению Дебая—Хюккеля. Здесь использована та методика расчета среднесолевым методом, которая кратко была
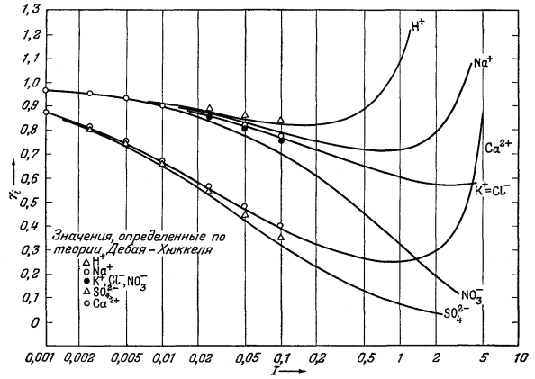 |
| Рис. 2.15. Зависимость коэффициентов активности индивидуальных
ионов от ионной силы раствора для некоторых обычных ионов. Сплошными линиями показаны значения, рассчитанные среднесолевым методом. Значения, определенные методом Дебая-Хюккеля по уравнению (2.76), вычислены при 108/a°i, = 9 для Н+; 4 для Na+; 3 для К+, С1—, NO—3; 6 для Са2+; 4 для SO2—4. При I < 0,01 значения gi, рассчитанные по методу Дебая—Хюккеля, для всех рассматриваемых одновалентных ионов одинаковы (в пределах ошибки эксперимента). |
рассмотрена выше. В этом случае мы исходили из допущения, что gK+ = gCl— = g±KCl. Затем по уравнениям (2.71) или (2.72) были рассчитаны значения gH+, gNa+ и gCa2+; при этом использовались величины средних коэффициентов активности соответствующих хлоридов. Значения gNO—3 рассчитывались исходя из соотношения
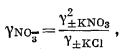 |
(2.79) |
а значения gSO2—4 - по уравнению (2.73).
Вычисление коэффициентов активности по теории Дебая - Хюккеля проводилось с помощью уравнения (2.76); при этом использовались соответствующие значения констант А, В и a°i, приведенные в качестве примера в табл. 2.6 и 2.7. Подобные расчеты для ионов в водном растворе при 25° С (и давлении 1 атм) проделаны Клотцем и в удобной табличной форме сведены в его книге [12, стр. 332].
При анализе Рис. 2.15 следует обратить внимание на то, что значения gi, для всех одновалентных ионов быстро сближаются как друг с другом, так и с предельными величинами, вычисленными по теории Дебая - Хюккеля; это сближение происходит при значениях ионной силы, меньших примерно 0,02. За исключением нитрат-иона, значения коэффициентов активности, рассчитанные по теории Дебая - Хюккеля и по среднесолевому методу, достаточно близко совпадают вплоть до ионной силы I = 0,1. Значения коэффициентов активности для двух двухвалентных ионов SO2—4 и Са2+ больше различаются между собой и более далеки от значений по Дебаю - Хюккелю. Однако практически можно считать, что величины коэффициентов активности индивидуального иона, рассчитанные этими двумя методами, достаточно близко совпадают при ионной силе раствора, не превышающей примерно 0,05.
Вспомним, что активность чистой жидкости при 1 атм общего давления и при данной температуре считается равной единице. Таким образом, активность чистой воды при тех же условиях также будет равна единице. Кроме того, активность любого вещества связана с его фугитивностью уравнением (2.18), которое в случае воды принимает вид
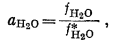
где f*H2O - фугитивность чистой воды. При умеренных давлениях водяной пар по своему поведению приближается к идеальному газу, а поэтому его фугитивность можно заменить парциальным давлением:
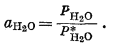 |
(2.80) |
Отсюда следует, что активность воды в растворе любого электролита определить нетрудно: для этого нужно лишь измерить давление водяного пара над раствором при постоянной известной температуре и разделить полученное значение на величину давления пара чистой воды при той же температуре. Величины давления водяных паров при различных температурах приведены в приложении 4.
Таблицы значений активности воды в растворах некоторых электролитов имеются в работе Робинсона и Стокса [24, приложения 8.3, 8.5]. По данным, заимствованным из этих таблиц, для NaCl, KC1 и CaCl2 при 25° С построены кривые (Рис. 2.16). Диаграмма Рис. 2.16 иллюстрирует зависимость активности воды от концентрации раствора; при расчете концентрации учтено общее число всех растворённых частиц. Так, 1-моляльный раствор NaCl или КСl рассматривается как 2-моляльный (моляльность растворенных частиц суммируется); 1-моляльный раствор CaCl2 - как 3-моляльный и т. д. Анализ диаграммы показывает, что построенные таким образом кривые активностей воды для растворов этих трех солей в области разбавленных растворов сливаются в одну прямую.
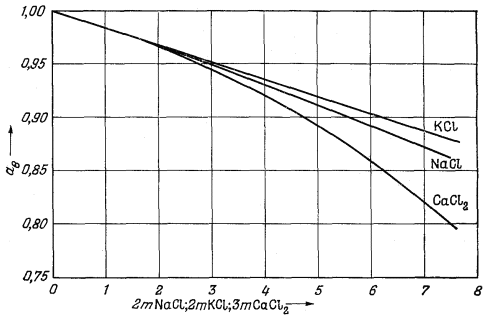 |
| Рис. 2.16. Соотношение между активностью воды aB и величиной nm для растворов некоторых электролитов при 25° С [24, приложения 8.3, 8.5]. |
Это явление можно объяснить следующим образом. Допуская, что в данном случае приложим закон Рауля в виде уравнения (2.13), имеем
| P1 = P*1N1 = P*1(1 — N2), | (2.81) |
где P1 - давление водяного пара над раствором электролита, Р*1 - давление пара чистой воды, N1 - мольная доля воды, a N2 - мольная доля суммы растворенных частиц. Для разбавленных растворов, согласно уравнению (2.38),
| N2 = knm, | (2.82) |
где n - число ионов, на которые диссоциирует электролит. Подставив выражение (2.82) в уравнение (2.81) и сделав соответствующие преобразования находим, что
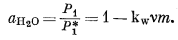 |
(2.83) |
Согласно определению множителя k [уравнение (2.38)], значение kw составляет
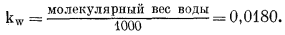
Предельный наклон кривых на диаграмме Рис. 2.16 соответствует значению 0,017.
Соотношение, определяемое уравнением (2.83), является предельным; его можно считать справедливым лишь для разбавленных растворов. Чтобы точно определить активность воды для более высококонцентрированных растворов, следует обратиться к экспериментальным данным. Соответствующие сведения о давлении водяного пара или о снижении давления пара — воды над растворами различных электролитов в зависимости от температуры и концентрации опубликованы в нескольких работах [11; 7, стр. 2467-2468]
При сочетании уравнений (2.81) и (2.82) мы получаем
| DP1 = P*1 — P1 = P*1kwnm. | (2.84) |
Другими словами, в случае разбавленных растворов в условиях постоянной температуры снижение давления водяного пара DP1 над раствором электролита происходит только при изменении произведения nm. Таким образом, все электролиты с одинаковым строением молекулы при условии полной диссоциации характеризуются одинаковым понижением давления пара при данной (низкой) концентрации. Это следует из того, что для солей типа KCl, BaSO4 и вообще для всех солей, молекула которых построена по типу АВ, величина n будет равна 2, для соединений типа CaCl2 n = 3, для АlСl3 n = 4 и т. д. Внимательный анализ значений DP1 для различных электролитов показывает, что уравнение (2.84) для многих веществ является достаточно близким приближением. Установлены, однако, и существенные исключения. Например, хотя для КСl DP1 = 12,2 мм рт. ст. при 0,5-моляльном растворе, для MgSO4 также при 0,5-моляльном растворе DP1 = 6,5 мм рт. ст., причем в обоих случаях величина DP1 измерялась при одинаковой температуре 100° С. Этот факт свидетельствует о том, что MgSO4 в умеренно концентрированных растворах в значительной степени находится в виде ионной пары MgSO°4. Подобные отклонения DP1 установлены при образовании комплексных ионов или при взаимодействии ионов с растворителем. Вопрос о поведении комплексных ионов в водных растворах будет подробно рассмотрен в гл. 4.
Скорость изменения активности воды с повышением температуры в пределах от 0 до 100° С ничтожно мала, если концентрация растворенного электролита невысокая. С увеличением концентрации зависимость активности воды от температуры становится более заметной. Это подтверждается данными для растворов H2SO4, приведенными в работе Харнеда и Оуэна 18, стр. 574-575]. Имеющаяся там диаграмма зависимости aH2О от mH2SO4 при 0, 25 и 60° С хорошо иллюстрирует высказанное нами положение.
Итак, при повышенных концентрациях значение активности воды справедливо лишь для той температуры, при которой проводились измерения; при малых концентрациях влияние температуры менее существенно. В частности, величины DP1, приведенные в Handbook of Chemistry and Physics [7], измерялись при 100° С. Строго говоря, отсюда следует, что значения активности, полученные на основании этих данных, справедливы лишь для данной температуры. Однако, как уже указывалось выше, в случае низких концентраций можно считать, что полученные таким образом величины активности отвечают 25° С без сколько-нибудь существенных отклонений.
Уравнение реакции для газа, находящегося в равновесии с водным раствором электролита при постоянной температуре, можно написать следующим образом (используем в качестве примера кислород):
| O2 газ = O2 водн. | (2.85) |
Константа равновесия К определяется соотношением активностей кислорода в жидкой и газовой фазах
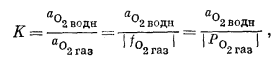 |
(2.86) |
где fO2 газ - фугитивность газообразного кислорода (в атмосферах), причем предполагается, что парциальное давление РO2 (также в атмосферах) достаточно низко, чтобы его можно было считать равным фугитивности.
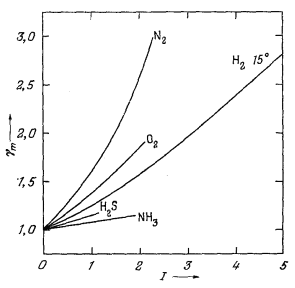 |
| Рис. 2.17. Коэффициенты активности gm для различных газов, растворенных в растворе NaCl при 25° С (Н2 при 15° С) [21]. |
Переписав уравнение (2.86) для любого газа с активностью из и отбросив символ || (при этом необходимо помнить, что Р2 имеет лишь численное значение), получим
| a2 водн = KP2 газ. | (2.87) |
поскольку A2 = g2m2, то
| g2m2 = KP2 газ. | (2.88) |
Принято, что коэффициент активности газа, растворенного в воде, не содержащей каких-либо иных растворенных веществ, равен единице. Обозначив моляльность такого раствора m0, а предельную концентрацию электролита в растворе символом ms, напишем
| gsms = KPs. | (2.89a) |
| m0 = KP0. | (2.89б) |
Из уравнений (2.89а) и (2.89б) выводится соотношение между коэффициентом активности газа, растворенного в растворе электролита, растворимостью газа в воде и в растворе этого электролита, а также равновесным парциальным давлением
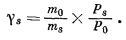 |
(2.90) |
Уравнение (2.90) и другие подобные соотношения создают основу для экспериментального определения величины g s. При постоянной величине Ps уравнение (2.89а) примет следующий вид:
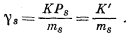 |
(2.91) |
Экспериментально установлено, что с повышением концентрации электролита в растворе при постоянном Ps величина ms обычно уменьшается. Следовательно, gs как правило, будет изменяться от единицы при нулевой концентрации растворенного электролита до величины, значительно превышающей единицу, при повышении ионной силы. Влияние концентрации электролита в растворе на уменьшение растворимости газов называется эффектом высаливания.
На Рис. 2.17 в виде функции ионной силы раствора электролита приведены значения коэффициентов активности gs для некоторых газов, присутствующих в растворе NaCl. Анализ диаграммы показывает, что скорость изменения коэффициента активности с повышением концентрации электролита в значительной мере зависит от конкретного газа. Данные, использованные при построении этой диаграммы, заимствованы из работы Рендалла и Фейли [21], где приведена большая таблица значений gs для нескольких газов, растворенных в растворах самых различных электролитов. Экспериментальная проверка этих данных показала, что для каждого газа величина gs значительно меняется в зависимости от вида электролита.
На Рис. 2.18 приведены значения коэффициента активности CO2, растворенного в растворах КСl или NaCl при 25° С. Исходные данные для построения диаграммы рассчитаны по уравнению (2.90). За основу взяты значения растворимости, определенные Маркамом и Кобе [19]. В работе этих авторов имеются данные по растворимости CO2 в растворах КСl, NaCl, KNO3, NaNO3, Mg(NO3)2, MgSO4 и Na2SC4 при температурах 0, 2, 25 и 40° С. Там же помещены аналогичные сведения по растворимости окиси азота.
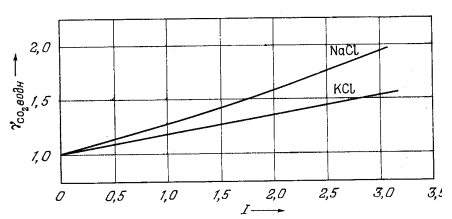 |
| Рис. 2.18. Коэффициенты активности CO2, растворенного в растворах NaCl и КСl при 25° С [18]. |
Осуществлены определения коэффициента активности недиссоцииро-ванной части слабых кислот, таких, как уксусная, растворенных в растворах различных электролитов [21, стр. 291]. Такой коэффициент определяет зависимость активности недиссоциированных, нейтральных молекул от концентрации тех же молекул: aнедисс = gнедиссmнедисс; индекс недисс обозначает недиссоциированную часть молекул. Коэффициент gнедисс является как бы антагонистом обычному среднему коэффициенту активности g±, для которого a1/22 = g±m2, где а1/22 и m2 относятся к сумме растворенного вещества.
Линейная зависимость, которую можно рассматривать как первое достаточно точное приближение при обработке экспериментальных данных, выражается следующим эмпирическим уравнением:
| lg gs = kmI. | (2.92) |
В этом выражении множитель кm называется коэффициентом солености (salting coefficient) (при моляльных единицах концентрации); I - ионная сила раствора. Сведения о величинах km для различных газов, нейтральных органических молекул и недиссоциированной части некоторых слабых органических кислот в самых разнообразных растворах электролитов имеются в работах Рендалла и Фейли [21, стр. 271, 285, 291], а также Харнеда и Оуэна [8, стр. 532-536, 736, 737].
Весьма желательно научиться точно рассчитывать коэффициенты активности различных нейтральных ионных пар в водном растворе типа МgSO°4 водн по величинам концентрации. Однако современный уровень наших знаний о ионных парах не позволяет осуществить такой расчет. Обычно когда такие ионные пары рассматриваются в области разбавленных или весьма умеренно концентрированных растворов, коэффициент активности ионной пары принимается равным единице. Если учесть различные допущения, принятые при вычислении констант диссоциации для ионных пар, это допущение вряд ли значительно снизит точность конечных результатов; данный вопрос будет рассмотрен ниже, в гл. 4.
Одна из наиболее важных реакций, которые нам необходимо рассмотреть,- реакция ионизации воды. Константа равновесия Кw для реакции
| H2Oжидк = H+водн + OH—водн, | (2.93) |
когда
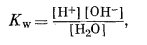 |
(2.94) |
точно измеряется несколькими различными методами. Значения Кw для температур от 0 до 60° С приведены в табл. 2.8. Эти значения получены путем измерения э. д. с. элементов без жидкого соединения.
Таблица 2.8
| t, °С | Kw ґ lO14 | t, °С | Kw ґ lO14 | t, °С | Kw ґ lO14 |
| 0 | 0,1139 | 25 | 1,008 | 45 | 4,018 |
| 5 | 0,1846 | 30 | 1,469 | 50 | 5,474 |
| 10 | 0,2920 | 35 | 2,089 | 55 | 7,297 |
| 15 | 0,4505 | 40 | 2,919 | 60 | 9,614 |
| 20 | 0,6809 |
Следует обратить внимание на то, что активность воды в уравнении (2.94) выступает в качестве знаменателя. Поэтому в ряде случаев в данное уравнение вообще не вводят значение [H2O], подразумевая тем самым, что активность воды равна единице. Из наших предыдущих рассуждений относительно снижения активности воды под влиянием растворенных в ней веществ должно быть ясно, что подобное допущение приложимо лишь к разбавленным растворам и не является справедливым для более концентрированных. Если нам нужно, например, рассчитать [ОН—] в умеренно концентрированном растворе по уравнению (2.94), то для этого мы должны знать точные значения и [Н+] и [H2O] в растворе.
В растворах электролитов взаимодействие между растворителем и растворенным веществом становится настолько сильным, что растворенное вещество в значительной мере диссоциирует на заряженные частицы. Природа взаимодействия ионов в растворе между собой и с растворителем сложным образом меняется с изменением концентрации. Установлено, что растворы электролитов подчиняются закону Генри, если учитывать диссоциацию растворенного вещества. Это положение создает хорошую основу для вывода основных соотношений между активностями и моляльными коэффициентами активности g, с одной стороны, и стандартными состояниями — с другой, для любого полиэлектролита. В области разбавленных растворов коэффициенты активности определяются по уравнению Дебая - Хюккеля
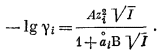
В случае более концентрированных растворов используется среднесолевой метод. Этот метод основан на предположении о полной диссоциации КС1 и равенстве коэффициентов активности ионов К+ и С1—; кроме того, при его применении учитывается понятие об ионной силе. С помощью среднесолевого метода коэффициенты активности индивидуальных ионов (катионов и анионов) рассчитываются по измеряемой величине среднего коэффициента активности соли. Все большее значение придается нейтральным и заряженным ионным парам, даже в умеренно концентрированных природных водах. Ионные пары усложняют расчет химических соотношений в природных водах, но все же помогают лучше понять поведение этих вод. В качестве примера приведены расчеты ионной силы, коэффициентов активности индивидуального иона для различных ионных частиц, а также влияния электролитов на растворение газов. Рассмотрено также влияние растворенных электролитов на активность воды как растворителя.
2.1. В резервуаре объемом
1000 мл содержится 0,05 моль газа при 25° С. Измеренное
давление газа составляет 1,02
атм.
а. Каково будет рассчитанное
давление, если принять, что данный газ подчиняется закону идеального
газа?
б. Каков коэффициент активности
(c) этого
газа?
Ответ: (а) Ррасч
= 1,22 атм; (б) c =
0,83.
2.2. Определить величину
коэффициента активности СО2 газ при давлении 500 атм и
температуре 500° К. Какова активность этого газа в данных условиях?
(Используйте Рис. 2.3 и табл.
2.1.)
Ответ: cCO2 = 0,78;
aCO2 =
390.
2.3. Какова активность СО2
газ в смеси 3 моль СО2 и 3 моль
O2 при общем давлении 700 атм и температуре 300°
С?
Ответ:
аCO2 =
329.
2.4. Рассчитайте фугитивность и
активность хлороформа в его растворе с ацетоном, если мольная доля
хлороформа составляет 0,25 (Рис.
2.5).
Ответ:
fCHCl3 @ 0,06
атм; аCHCl3 @
0,16.
2.5. Установлено, что стронций
замещает кальций в арагоните. Частный химический анализ дал следующие
значения:
| СаО | 0,05 моль; |
| SrO | 0,005 моль; |
| CO2 | 0,055 моль. |
| С1 | 18980 | Са | 400 |
| Na | 10561 | К | 380 |
| Mg | 1272 | Br | 65 |
| S | 884 | С | 28 |
1. C o n w a y В. Е. Eleotrochemical Data, New York, Elsevier, 1952.
2.C r a w f o r d J. G. Water analysis, Subsurface Geologic Methods, Colorado School of Mines, 193, 1951.
3. D a r k e n L. S., G u r г у R. W. Physical Chemistry of Metals, New York, McGraw-Hill, 210, 1953. (Есть русский перевод: Д а р к е н Л. С., Г у р р и Р. В. Физическая химия металлов, М., Металлургиздат, 1960.)
4. Е 11 i о t t J. F., С h i р m a n J. Trans. Faraday Soc., 47, 138, 1951.
5. G a m s о n В. W., W a t s o n К. M. National Petroleum News, Tech. Section, 36, R623, Sept. 1944.
6. Handbook of Chemistry and Physics, 41st edition. Cleveland, Ohio, Chemical Rubber Publishing Co., 2303-2305, 1959.
7. Handbook of Chemistry and Physics, 43rd. ed., Cleveland, Ohio, Chemical Rubber, 2467-2468, 1961.
8. H a r n e d H. S., O w e n В. В. The Physical Chemistry of Electrolytic Solutions, 3rd ed. (ACS Monograph 137), New York, Reinhold, 532-536, 574-575, 638, 736, 737, 1958.
9. H i l d e b r a n d J. H., S c o t t R. L. Regular Solutions, Englewood Cliffs, N.J., Prentice-Hall, 1962.
10. Н о u g e n 0. A., W a t s o n К. M. Chemical Process Principles, Part II, Thermody- namics, copyring 1947 by John Wiley and Sons, Inc.
11. International Critical Tables, III, New York, McGraw-Hill, 1928.
12. К l o t z I. M. Chemical Thermodynamics, Englewood Cliffs, N.J., Prentice-Hall, 331, 1950.
13. L a t i m e r W. M. Oxidation Potentials, New York, Prentice-Hall, 354, 349-358, 1952. (Есть русский перевод: Л а т и м е р В. Окислительные состояния элементов и их потенциалы в водных растворах, М., ИЛ, 1954.)
14. L e w i s G. N., R a n d a 11 M. Journ. Am. Chem. Soc., 43, 1112, 1921.
15. L e w i s G. N., R a n d a l l M. Thermodynamics, New York, McGraw-Hill, chap. 28, 381, 1923. (Есть русский перевод: Л ь ю и с Г., Р е н д а л л М. Химическая термодинамика, ОНТИ, 1936.)
16. L e w i s G. N., R a n d a l l M. Thermodynamics, 2nd ed., revised by Pitzer K. S., Brewer L., New York, McGraw-Hill, chap. 23, 1961.
17. M а с I n n e s D. A. Journ. Chem. Soc., 41, 1086, 1919.
18. M a n о v G. G., В a t e s R. G., H a m e r W. J., А с r e e S. F. Journ. Am. Chem. Soc., 65, 1765, 1943.
19. M a r k a m А. А., К о b e К. А. Journ. Аш. Chem. Soc., 63, 449, 1941.
20. P a r s o n s R. Handbook of Electrochemical Constants, London, Butterworth, 1959.
21. R a n d a 11 M., F a i 1 e у С. F. Chem. Rev., 4, 271, 285, 291, 1927.
22. R a n d a l l M., S o s n i c k В. Journ. Am. Chem. Soc., 50, 967, 1928.
23. R o b i n s o n R. A., S t o k e s R. H. Molecular Interaction, Ann. N.Y. Acad. Sci., 51, 593, 1949.
24. R o b i n s o n R. A., S t o k e s R. H., Electrolyte Solutions, New York, Academic, chap. 3, appendices 8,3, 8,5, 1959.
25. R o s e n b e r g P. E. Am. Journ. Sci., 261, 689, 1963.
26. S a l s t r o m E.J. Journ. Am. Chem. Soc., 53, 1794, 3385, 1931.
27. S a 1 s t r о m E.J. Journ. Am. Chem. Soc., 54, 4252, 1932.
28. S a 1 s t r о m E. J., H i 1 d e b r a n d J. H. Journ. Am. Chem. Soc., 52, 4650, 1930.
29. S v e r d r u p H. U., J o h n s o n M. W., Fleming R.H. The Oceans, Englewood Cliffs, N. J., Prentice-Hill, Table 36, 176, 1942.
30. Z a w i d s k i J. v. Zeit. fur Phys. Chem., 35, 129, 1900.
D a r k e n L. S., G u r r y R.W. Physical Chemistry of Metals, New York, McGraw-Hill, 1953. (Есть русский перевод: Д а p к e н Л. С., Г у р р и Р. В. Физическая химия металлов, M., Металлургиздат, 1960.)
D e n b i g h K.G. The Principles of Chemical Equilibrium, New York, Cambridge, 1957.
H a r n e d H. S., 0 w e n B. B. The Physical Chemistry of Electrolytic Solutions, 3rd ed. (ACS Monograph 137), New York, Reinhold, 1958.
K 1 о t z I. M. Chemical Thermodynamics, Englewood Cliffs, N. J., Prentice-Hall, 1950.
L a t i m e r W. M. Oxidation Potentials, New York, Prenfice-Hall, 1952. (Есть русский перевод: Л а т и м е р В. Окислительные состояния элементов и их потенциалы вводных растворах, M., ИЛ, 1954.)
L e w i s G. N., R a n d a l l M. Thermodynamics, New York, McGraw-Hill, 1923. (Есть русский перевод: Л ь ю и с Г., Р е н д а л л M. Химическая термодинамика, ОНТИ, 1936.)
L e w i s G. N., R a n d a l l M., Thermodynamics, 2nd ed., revised by Pitzer K. S., Brewer L., New York, McGraw-Hill, 1961.
R o b i n s o n R. A., S t о k e s R. H. Electrolyte Solutions, New York, Academic, 1959.
|
|
|
|
[Содержание] [Глава 1] [Глава 3] |