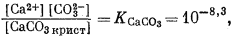
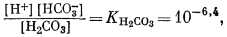
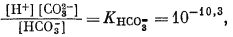
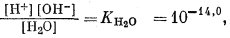
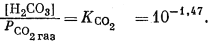
| Р.М. Гаррелс, Ч.Л. Крайст | Растворы, минералы, равновесия |
|
|
|
|
[Содержание] [Глава 2] [Глава 4] |
|
|
|
|
В карбонатных горных породах обычно сохраняются обильные остатки фауны и флоры, изучение которых дает ценные сведения о геологическом прошлом Земли. Но этим не ограничивается интерес геологов к карбонатным породам. Раз эти породы образовались в результате химического осаждения из когда-то существовавшей водной среды, то по составу слагающих их минералов мы можем судить об условиях отложения и последующего изменения таких пород, конечно располагая достаточным количеством данных. Этому вопросу посвящено множество работ, одно лишь перечисление которых заняло бы очень много места. В настоящей книге разбирается всего несколько характерных случаев, которые могут встретиться в геологической практике. Для этих случаев ряссматривается методика определения равновесных условий карбонатов и дается техника вычисления активности ионов металлов, находящихся в равновесии с твердыми карбонатами. Кроме того, рассмотрен вопрос об определении фактической растворимости металлов в виде катионов.
Значения растворимости карбонатных минералов, опубликованные в литературе, многочисленны, но разноречивы. Одна из причин таких расхождений - отсутствие достаточно высокой степени точности подобных исследований. Так, например, среди значений растворимости наиболее удовлетворительные данные получены для минералов, подобных повеллиту, СаМоO4. Для определения же разницы в величинах растворимости таких двух минералов, как кальцит и арагонит (свободные энергии образования которых различаются всего на 0,2-0,5 ккал), требуется проделать огромную работу. Другая причина (на ней мы остановимся ниже) заключается в том, что при использовании большого числа переменных, необходимых для определения растворимости карбонатных минералов, у исследователей появляется тенденция сравнивать значения растворимости, полученные в условиях, лишь кажущихся одинаковыми, но в действительности различных. Помимо всего прочего, карбонатные минералы обладают в высшей степени непостоянным составом. Прежде чем перейти к рассмотрению возможного влияния колебаний состава этих минералов на условия равновесия, рассмотрим растворимость предельно чистого кальцита как функцию других переменных.
Итак, рассмотрим пять
случаев. Здесь выбраны такие группы условий, которые охватывают
значительную часть возможных геологических ситуаций, а большая часть
других может быть получена путем комбинации и перестановки рассмотренных.
Для удобства наши вычисления будут относиться только к кальциту, но
аналогичные выкладки могут быть произведены и при определении
растворимости любых других карбонатов. Вот эти пять характерных групп
условий:
1. Реакции, происходящие при
погружении чистого карбоната в чистую воду с ничтожным участием газовой
фазы.
2. Реакции кальцита в чистой воде,
но в системе, открытой в отношении СО2 (например, в контакте с
атмосферой) с определенным парциальным давлением
СО2.
3. Равновесные
соотношения в системе с данным количеством растворенных карбонатных
компонентов и при произвольно выбранном значении рН, т. е. когда
равновесия в системе контролируются другими
реакциями.
4. Равновесие в системе с
произвольным значением рН, соединенной с внешним резервуаром,
характеризующимся данным парциальным давлением
СО2.
5. Равновесие,
возникающее в результате добавления СаСО3 к системе,
первоначально открытой в отношении CO2, но затем, перед
добавлением СаСО3, закрытой.
Первый случай может рассматриваться применительно к определению растворимости кальцита - это закрытая система СаСО3- Н2О. Так как столь простая система практически никогда не встречается, она мало интересна в геологическом отношении.
Второй случай представляет значительный интерес для геологов, так как отражает соотношения, существующие в озерах, реках и других природных разбавленных растворах, которые находятся в непосредственном контакте с атмосферой и рН которых полностью контролируется равновесиями карбонатов.
Третий случай затрагивает круг вопросов, связанных с анализами подземных вод. Подобные анализы обычно дают общую сумму растворенных карбонатов (НСО—3 + СО2—3 + Н2СО3), концентрацию кальция и рН. Но находится ли такой раствор в равновесии с кальцитом? И находится ли он в равновесии с атмосферой? И если отсутствует анализ на кальций, но известно, что система находится в равновесии с кальцитом, то можно ли рассчитать концентрацию иона кальция?
Четвертый случай также имеет большое значение для геологии. Если известно, что система находится в равновесии с СО2 при данном парциальном давлении и что она характеризуется данным значением рН, какими бы факторами это значение не контролировалось, то какова активность иона кальция в равновесии с кальцитом? Что необходимо знать, чтобы приблизительно вычислить растворимость кальцита в такой системе?
Пятый случай можно проиллюстрировать на примере дождевой воды, которая находится в равновесии с атмосферой и, просачиваясь в землю через нереакционноспособную почву, приходит в соприкосновение с кальцитом. Каковы будут активность и концентрация иона кальция в растворе, когда тот достигнет равновесия? Каков равновесный рН воды?
Расчеты, приводимые в настоящей главе, непосредственно приложимы к водам с малой ионной силой (Ј 0,1), т. е. справедливы для озерных и речных вод, а также для питьевых грунтовых вод, в которых образование комплексных ионов незначительно. О роли комплексообразования в более концентрированных растворах см. в гл. 4.
Для всех пяти перечисленных случаев принципиальная схема решения остается одной и той же. Здесь принимает участие самое большее семь переменных величин при постоянной температуре и неизменном общем давлении, причем предполагается, что коэффициенты активности всех компонентов известны. К этим переменным относятся РCO2, aН2СО3, aHCO—3, aCO2—3, aH+, aOH—, aCa2+. Для каждого случая используются произведение растворимости CaCO3, первая и вторая константы диссоциации угольной кислоты и константа равновесия для воды, так как всегда ставится условием равновесие системы с СаСО3 и предполагается равновесие всех ионов в растворе между собой. Итак, использованы следующие пять уравнений (числовые значения констант равновесия рассчитаны для 25° С):
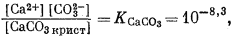 |
(3.1) |
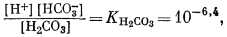 |
(3.2)1 (стр.75) ) |
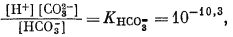 |
(3.3) |
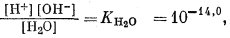 |
(3.4) |
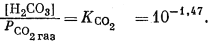 |
(3.5) |
В перечисленных выше уравнениях все компоненты считаются растворенными в воде, за исключением двух, помеченных соответствующими подстрочными индексами СаСО3 крист и СО2 газ. Точные значения констант равновесия для температур от 0 до 80° приведены в табл. 3.2; вопрос о величине KH2O рассмотрен в гл. 2. Поскольку при решении уравнений для наших пяти случаев используются различные допущения, степень точности численных значений констант равновесия для уравнений (3.1) - (3.5) вполне достаточна.
Уравнения (3.1) - (3.5) дают основу для расчетов любых услoвий в пределах пяти рассматриваемых случаев. Необходимость дополнительных уравнений диктуется специально выбранными условиями.
Итак, избыток чистого СаСО3 помещен в чистую воду (используемая в опытах вода осовобождается от реакционноспособных газов, например CO2, путем пропускания через нее инертных газов - азота или гелия). Последующий процесс можно представить себе следующим образом: ионы кальция и карбонат-ионы диссоциируют в воде. При этом происходит частичная гидратация ионов Са2+, что существенной роли не играет; вместе с тем взаимодействие карбонат-ионов с водой выражается такой последовательностью реакций:
| CO2—3 водн + H2Oжидк = HCO—3 водн + OH—водн, | (3.6a) |
| HCO—3 водн + H2Oжидк = H2CO3 водн + OH—водн. | (3.6б) |
Раствор становится щелочным, поскольку освобождаются ионы ОН—. Существенное значение имеет и третья реакция:
| Н2СО3 водн = СО2 газ + Н2Ожидк. | (3.7) |
|
1 (стр.75) Водные растворы двуокиси углерода наряду с молекулами СО2 содержат молекулы угольной кислоты H2CO3. Насколько известно, проводилось изучение равновесии с участием этих двух компонентов, причем константы равновесия, определенные из отношения [СО2]/[Н2СО3], равны приблизительно 386. Не обращая внимание на допущения, сделанные относительно коэффициентов активности, свойственных этим двум различным компонентам - СО2 и Н2СО3, отметим, что отношение числа молекул СО2 к числу молекул Н2СО3 в растворе двуокиси углерода в чистой воде значительно превышает единицу. Несмотря па эти данные, всю растворенную двуокись углерода обычно связывают с Н2СО3 и для определения первой константы диссоциации используют уравнение (3.2); здесь мы будем следовать той же практике. Наши выводы от этого нисколько не пострадают, ибо в термодинамике гидратированное состояние растворенных компонентов не учитывается. Все эти вопросы подробно рассмотрены Керном [4]. |
Однако, согласно принятым нами условиям, для первого случая присутствие газовой фазы ничтожно1 (стр.76) ; следовательно, уравнение (3.7) к разбираемому нами случаю отношения не имеет.
Итак, для данной системы основное значение имеют такие компоненты, как Сa2+водн, CO2—3 водн, HCО—3 водн, Н2СО3 водн, ОН—водн, Н+водн, CaСO3 крист и Н2Ожидк. При этом активность СаСО3 крист равна единице, а для Н2Ожидк она также может считаться равной единице, так как по условию раствор является разбавленным. Таким образом, остается только шесть переменных величин. Для расчета этой системы можно использовать уравнения (3.1) - (3.4), но, чтобы получить решение для шести переменных, нужно составить еще два уравнения.
Так как первоначально карбонатные компоненты в воде отсутствовали, то теперь каждому компоненту раствора, содержащему атом углерода, должен соответствовать ион кальция. Это обусловлено тем, что источником и тех и других служит кальцит, который не может диссоциировать таким образом, чтобы свободного кальция в растворе оказалось больше, чем углерода, или наоборот, без возникновения электрического заряда. Тогда мы вправе написать
| mCa2+ = mCO2—3 + mHCO—3 + mH2CO3 | (3.8) |
Кроме того, раствор должен оставаться нейтральным, так чтобы сумма положительных зарядов на катионах была равна сумме отрицательных зарядов на анионах. Памятуя, что и ион кальция, и карбонат-ион несут двойной заряд, мы можем составить следующее уравнение для электрически нейтральной системы:
| 2mCa2+ + mH+ = 2mCO2—3 + mHCO—3 + mOH—. | (3.9) |
Уравнения (3.8) и (3.9) в сочетании с уравнениями (3.1)- (3.4) составляют те шесть уравнений, которые необходимы для решения нашей задачи с шестью неизвестными, но при одном условии: поскольку уравнения (3.1) - (3.4) составлены в выражениях активности, а уравнения (3.8) и (3.9) - в выражениях молялъности, решение задачи окажется верным только в том случае, если mi @ ai или gi = 1.
В большей части известных в литературе примеров решения подобной задачи такую оговорку не учитывают. Поэтому прежде всего необходимо разобраться в предпосылках для данного допущения, а также продумать методику, необходимую для строгого решения. На первый взгляд дилемма представляется безнадежной, поскольку значения gi не могут быть определены прежде, чем будет установлена ионная сила, а ионная сила не может быть вычислена прежде, чем будет решена сама задача. Но эту трудность можно обойти, используя серию последовательных приближений. Сначала задача решается, исходя из предположения о том, что коэффициенты активности равны единице, и таким образом определяется ионная сила. Затем вычисляются коэффициенты активности и задача решается заново до получения нового значения ионной силы. Так поступают до тех пор, пока разница между величинами, полученными при двух последовательных приближениях, не станет незначительной.
Итак, теперь необходимо
решить задачу при допущении, что mi =
аi, ибо вначале сделать такое решение более строгим
невозможно. Поскольку обратная подстановка в шесть уравнений дело
несложное, следует также уже в первом приближении выяснить, нет ли Других
способов упрощения. На основании уравнений (3.5) и (3.6) делаем
заключение, что раствор будет более щелочным, чем исходная вода, т. е.
окончательное значение рН будет
|
1 (стр.76) В экспериментальном отношении это соответствует раствору, насыщенному СаСО3 и находящемуся в контакте е избытком СаСО3, который полностью погружен в сосуд. |
выше 7. Если величина рН будет, например, равна 8, то из уравнения (3.2) получим
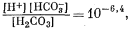
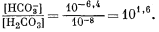
Таким образом, величина [Н2СО3] оказывается много меньше значения [НСО—3], и в первом приближении ею можно пренебречь. Если рН і 8, то величина [Н+] Ј 10—8 и ее также можно временно не учитывать. Поэтому остаются следующие равенства:
| [Ca2+] [CO2—3] = 10—8,3, | (3.1a) |
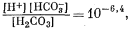 |
(3.2) |
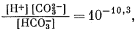 |
(3.3) |
| [H+] [OH—] = 10—14,0, | (3.4a) |
| [Ca2+] = [CO2—3] + [HCO—3], | (3.8, видоизмененное) |
| 2[Ca2+] = 2[CO2—3] + [HCO—3] + [OH—]. | (3.9, видоизмененное) |
Умножая уравнение (3.8, видоизмененное) на 2 и вычитая его из уравнения (3.9, видоизмененное), получаем
| [HCO—3] = [OH—]. | (3.10) |
Простейший путь решения, вероятно, заключается в том, чтобы выразить все,уравнения равновесия через [Н+] и подставить их в уравнение (3.8, видоизмененное). Из уравнения (3.4а) находим, что
[H+] [OH—] = 10—14,
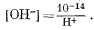
Подставляя из уравнения (3.10), получаем
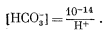 |
(3.11) |
Подставляя уравнение (3.11) в уравнение (3.3), имеем
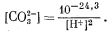 |
(3.12) |
Подставляя уравнение (3.12) в уравнение (3.1а), получаем
| [Ca2+] = 1016[H+]2. | (3.13) |
И наконец, используя равенства (3.11), (3.12) и (3.13) в уравнении (3.8, видоизмененное), получаем
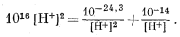 |
(3.14) |
Умножив все члены этого уравнения на [Н+]2 и преобразовав его, получим
| 1016[H+]4 — 10—14[H+] = 10—24,3. | (3.15) |
Этот простейший способ "проб и ошибок" приводит нас к следующему результату: [Н+] = 10—9,95.
Обратная подстановка в уравнения (3.13), (3.12), (3.11) и (3.10) дает следующие величины:
[Ca2+] =
10—3,9,
[CO2—3] =
10—4,4,
[HCO—3] =
10—4,05,
[OH—] = 10—4,05.
Ясно, что пренебрежение величиной [Н+] в уравнении электрического равновесия (3.9) не приводит к ощутимой ошибке и что равным образом оправдано пренебрежение величиной [Н2СО3] в уравнении (3.8) (согласно уравнению (3.2), [Н2СО3] равна 10—7,6).
Теперь рассмотрим ошибку, которая возникает при допущении, что gi = 1. Вычислим ионную силу нашего раствора1 (стр.78):
I = 1/2 ([Ca2+] ґ 22 + [H+] ґ 12 + [CO2—3] ґ 22 + [HCO—3] ґ 12 + [OH—] ґ 12),
I = 1/2 (5,0 ґ 10—4 + 1,1 ґ
10—10 + 1,6 ґ 10—4 + 8,9
ґ 10—5 + 8,9 ґ 10—5),
I = 4,2 ґ 10—4.
Очевидно также, что подобное значение ионной силы допускает применение уравнения Дебая-Хюккеля (2.76). Взяв для gCa2+ соответствующие значения констант из табл. 2.6 и 2.7, находим, что
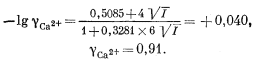
Сходным образом определяем, что gCO2—3 = 0,91, gHCO—3 = 0,98, gOH— = 0,98, gH+ = 0,98, gH2CO3 = 1.0 (молекулярные частицы). Все эти коэффициенты весьма близки к единице, так что ошибка, возникающая при пренебрежении ими, несущественна. Но для полноты картины разберем наш первый случай с использованием этих коэффициентов.
Выразив все уравнения через значения моляльности и коэффициенты активности, получаем
| mCa2+gCa2+mCO2—3gCO2—3 = 10—8,3, | (3.1a) |
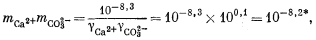 | |
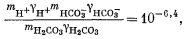 | |
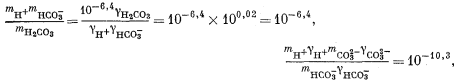 |
(3.3) |
|
1 (стр.78) Как было отмечено выше, на данной стадии ионную силу необходимо рассчитывать по активностям, а не по моляльностям. После определения величины gi, как показывают последующие расчеты, можно вычислить величину mi, затем, используя эту величину mi, определяется новое значение I, а затем весь этот процесс повторяется. Однако при низком значении ионной силы величина gi меняется незначительно, и, таким образом, подобные вычисления целиком можно и не проводить. |
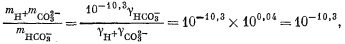 | |
| mH+gH+mOH— = 10—14,0, | (3.4a) |
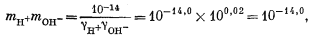 | |
| mCa2+ = mHCO—3 + mCO2—3, | (3.8a) |
| 2mCa2+ = 2mCO2—3 + mHCO—3 + mOH—. | (3.9a) |
Следовательно, единственное заметное изменение результата (в пределах точности наших вычислений) устанавливается лишь в величине константы по уравнению (3.1а), отмеченному звездочкой. Таким образом, подстановка новых значений в каждое уравнение равновесия дала бы изменение только в одном из них, а уравнение, аналогичное уравнению (3.15), приняло бы следующий вид:
1016,1[H+]4 — 10—14[H+] = 10—24,3.
Такое изменение вызывает некоторое понижение равновесного значения рН примерно до 9,9, но в целом расхождение, установленное в результате пересчета, не выходит за пределы точности учитываемых констант. Однако использованная методика расчета отражает все моменты, необходимые для правильных вычислений равновесных условий других карбонатов, если коэффициенты активности слишком малы, чтобы их учитывать.
Подводя итоги разбора первого случая, можно сказать, что равновесное значение рН лежит между 9,9 и 10 и что mCa2+ @ 10—3,9, mCO2—3 @ 10—4,4, mHCO—3 @ 10—4,05, mH2CO3 @ 10—7,6. Эти теоретические значения хорошо совпадают с экспериментальными данными. При измерении равновесного значения рН по отношению к измельченному кальциту в дистиллированно и деаэрированной воде в трех опытах Гаррелс и Сивер получили результаты, равные 9,88; 9,92 и 9,96. Как указывалось ранее, эта система мало интересна для геологов, поскольку она слишком проста. Это положение иллюстрируется "характеристическими уравнениями"; лишь для немногих природных систем можно допустить образование растворенных карбонатных компонентов, происходящих лишь ИЗ одного твердого карбоната, а также принять что соотношения ионов в них могут быть выражены через одни только активности ионов кальция, водорода, карбоната, бикарбоната и гидроксила.
Второй случай, когда кальцит находится в равновесии с водой при данном парциальном давлении CO2, можно экспериментально получить из первого случая, если открыть резервуар с кальцитом и водой и непрерывно пропускать через него воздух или какой-нибудь другой газ с постоянным содержанием CO2. Уравнения (3.1) — (3.5) подойдут и для этого случая.
Однако уравнение (3.8) теперь не имеет силы, поскольку карбонатные компоненты привносятся в раствор не только из кальцита, но и из внешнего источника CO2. Уравнение (3.9), отражающее электрическую нейтральность системы, остается справедливым, так как в растворе присутствуют все те же ионы Са2+, H+, СО2—3, НСО—3 и ОН—. Отсюда
| 2mCa2+ + mH+ = 2mCO2—3 + mHCO—3 + mOH—. | (3.9) |
Вместо уравнения (3.8) можно ввести новые уравнения, отражающие конкретное условие — постоянство давления СО2:
| PCO2 = K. | (3.16) |
Из уравнения (3.5) следует, что
| [H2CO3] = 10—1,5 PCO2. | (3.17) |
Теперь уравнения (3.1) - (3.4), (3.9) и (3.17) будут характеризовать систему при данном РCO2. Для примера рассчитаем равновесные соотношения с атмосферой, в которой РCO2 @ 10—3,6. Из уравнения (3.17) находим, что
| [H2CO3] = 10—1,5 ґ 10—3,5 = 10—5,0. | (3.18) |
Далее необходимо выразить уравнение (3.9) через [Н+]. Для этого в качестве первого приближения допускаем, что gi @ 1 и ai @ mi. Тогда из уравнения (3.2) получаем
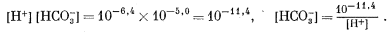 |
(3.19) |
Из уравнения (3.3) имеем
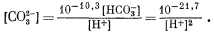 |
(3.20) |
Из уравнения (3.4а)
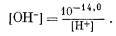 |
(3.21) |
Из уравнения (3.1а)
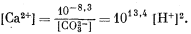 |
(3.22) |
Подставив полученные значения, т. е. уравнения (3.19)-(3.22), в уравнение (3.9), найдем
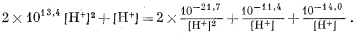
Теперь умножим все члены уравнения на [Н+]2 и выразим цифровые величины соответствующей степенью десяти:
1013,7 [H+]4 + [H+]3 = 10—21,4 + 10—11,4[H+] + 10—14[H+].
Приведем подобные члены уравнения
| 1013,7 [H+]4 + [H+]3 — 10—11,4[H+] = 10—21,4 | (3.23) |
и решим его методом "проб и ошибок":
[Н+] = 10—8,4.
Отсюда
[Ca2+] = 10—3,4,
[CO2—3] = 10—4,9,
[HCO—3] = 10—3,0;
[OH—] =
10—5,6, [H2CO3] = 10—5,0.
Итак, рН системы, состоящей из CaCO3 в воде и находящейся в равновесии с атмосферой, равен 8,4. Ионная сила для данного случая так мала, что вносимые коррективы на разницу величин моляльности и активности не поддаются учету. Моляльность Са2+ равна примерно 10—3,4, т. е. в 3,2 раза выше, чем в первом случае (в отсутствие контакта с атмосферой). Обращает на себя внимание существенное понижение величины рН, обусловленное влиянием атмосферного СО2. Это означает, что определения рН природных вод, не имеющих контакта с атмосферой, могут оказаться неточными, если перед замером рН взятая проба придет в соприкосновение с воздухом. Эксперименты, проведенные Гаррелсом совместно с Сивером, показали прекрасное соответствие рассчитанного значения рН воды, находящейся в равновесии с кальцитом и атмосферой, и величины рН, полученной экспериментальным путем.
Вероятно, именно с третьим случаем геологи и геохимики встречаются наиболее часто. В нашем распоряжении имеются данные химического анализа природной воды, на основании которых можно определить величину рН, валовую концентрацию кальция и валовую концентрацию карбонатных компонентов, а также значение ионной силы. Но находится ли вода в равновесии с карбонатом кальция или же она им пересыщена или недосыщена? Приближенно эту задачу можно решить, но в частном случае, касающемся морской воды, при ее решении возникали длительные, а иногда и ожесточенные споры. На этом вопросе мы подробно остановимся в гл. 4.
Методика расчета для третьего случая заключается в составлении необходимых уравнений в выражениях моляльности и коэффициентов активности:
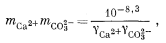 |
(3.1a) |
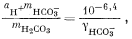 |
(3.2a)1 (стр.81) |
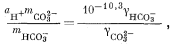 |
(3.3) |
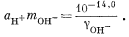 |
(3.4) |
Валовая концентрация карбоната определяется по данным анализа:
| mH2CO3 + mHCO—3 + mCO2—3 = kанал, | (3.24) |
аналитически установлена и величина рН:
| aH+ = kH+. | (3.25) |
Теперь наша система охарактеризована шестью уравнениями: (3.1) — (3.4), (3.24) и (3.25), а также известной по результатам анализа величиной ионной силы. Все это позволяет нам рассчитать приблизительные значения всех коэффициентов активности.
В качестве примера частного решения данной задачи возьмем какой-нибудь анализ природной воды и попытаемся определить, не находится ли эта вода в равновесии с кальцитом. Выбранный нами анализ (табл. 3.1) характеризует состав воды из озера Эри в Калифорнии [1, стр. 70].
Пересчет этих данных без
учета F, NО3 и В показывает, что ионная сила раствора равняется
0,140; mCа2+ равна 0,002 (10—2,7),
а mHCO—3 составляет 0,0014
(10—2,85).
|
1 (стр.81) Поскольку дана величина рН, известна и aH+; величина же mH+ почти никогда не используется в характеристических уравнениях. Кроме того, значение gH2CO3 в природных водах столь близко к единице, что его не следует принимать во внимание, за исключением отдельных особо точных исследований. |
Таблица 3.1
| PН | Са | Mg | Na | К | НСО3 | СО3 | SO4 | Cl | F | NO3 | B |
| 7,5 | 79 | 261 | 2110 | 4,0 | 84 | 0 | 508 | 3790 | 0,1 | 1,2 | 1,1 |
В анализах подобного типа концентрации СО2—3 и H2CO3 могут и не определяться; как мы убедимся позднее, их расчетная концентрация окажется ниже разрешающей способности химического анализа. Индивидуальные ионы характеризуются следующими коэффициентами активности1 (стр.82) : gCa2+ = 0,35, gHCO—3 = 0,77, gCO2—3 = 0,35.
Подставив значения аH+, mHCO—3, gHCO—3 и gCO2—3 в уравнение (3.3), получим
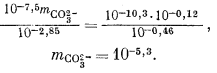
Используем полученную величину, а также значения gCa2+ и gCO2—3 в уравнении (3.1а):
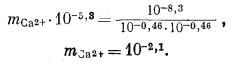
Таким образом, согласно нашим расчетам, равновесная концентрация кальция составляет 10—2,1, тогда как аналитическая концентрация кальция равна 10—2,7. Отсюда следует, что наша вода несколько недосыщена по отношению к карбонату кальция.
Подобные вычисления можно продолжить и показать, что величина mHCO—3, полученная при химическом анализе, значительно превышает величину mHCO—3, которую можно было бы ожидать для раствора, находящегося в равновесии с атмосферой при указанном значении рН = 7,5. Расчетная величина mHCO—3 оказывается равной 10—3,8 в отличие от аналитической, которая составляет 10—2,9. Если считать, что данная концентрация бикарбоната отражает равновесное состояние воды по отношению к атмосфере, то равновесное значение рН было бы выше 8. А раз так, то при подобном более высоком значении рН наша вода была бы близка к насыщенной по отношению к карбонату кальция. Отсюда мы вправе предположить, что измерение рН производилось в низкой точке цикла его суточной вариации.
Четвертый случай, вероятно,
ближе всего отвечает расчетам, целью которых является определение
активности и моляльности иона кальция в состоянии равновесия с кальцитом
при любых возможных условиях. Например, каковы будут значения активности и
моляльности иона кальция в растворе с ионной силой, равной 0,10, при рН,
достигающем 10 вследствие взаимодействия с вулканическим стеклом, если
этот раствор контактирует с атмосферой и содержит твердый карбонат
кальция?
|
1 (стр.82) Величина gCa2+ определена по фиг. 2.15; значения gHCO—3 и gCO2—3 получены соответственно с кривых А и D на фиг. 4.5. |
Здесь можно использовать уравнения (3.1а), (3.2а), (3.3) и (3.4а), а также характеристические уравнения, отражающие постоянство РCO2 и известные величины рН. Вот эти выражения:
| mCa2+gCa2+mCO2—3gCO2—3 = 10—8,3, | (3.1a) |
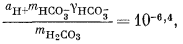 |
(3.2a) |
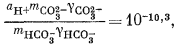 |
(3.3) |
| aH+mOH—gOH— = 10—14,0, | (3.4a) |
| aH+ = kH+, | (3.25) |
| mH2CO3 = 10—1,5PCO2, gH2CO3 = 1. | (3.17a) |
Прежде всего следует определить коэффициенты активности индивидуальных ионов. При ионной силе, равной 0,1, для этого можно воспользоваться как методом Дебая - Хюккеля, так и среднесолевым методом (гл. 2).
Если мы решим использовать теорию Дебая - Хюккеля, то найдем в табл. 2.6 и 2.7 соответствующие значения коэффициентов А и В, а также значение ai и после расчета по уравнению (2.76) получим, что gCa2+ = 0,40, gCO2—3 = 0,36, gHCO— = 0,78, gOH— = 0,76. Как и ранее, gH2CO3 без серьезной ошибки можно приравнять единице. Подставим найденные значения коэффициентов активности в составленные нами уравнения, а в уравнения (3.25) и (3.17а) - соответственно конкретные значения рН = 10 и РCO2 = 10—3,5 (наша система находится в равновесии с атмосферой). Далее переведем все выражения в единицы моляльности, за исключением аH+ которая известна из непосредственных измерений раствора:
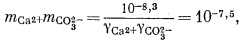 |
(3.1a) |
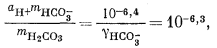 |
(3.2a) |
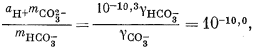 |
(3.3) |
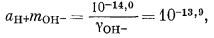 |
(3.4a) |
| aH+ = 10—10,0, | |
| mH2CO3 = 10—1,5PCO2 = 10—5,0. | (3.17a) |
Дальнейшие расчеты уже несложны. Перенесем значения mH2CO3 = 10—5,0 и аH+ = 10—10 из уравнений (3.17а) и (3.25) в уравнение (3.2а):
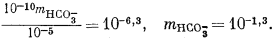
Подставим полученное значение в уравнение (3.3):
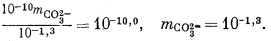
Тогда из уравнения (3.1) получаем
10—1,3mCa2+ = 10—7,5, mCa2+ = 10—6,2.
И наконец,
gCa2+
mCa2+ =
aCa2+,
10—0,4 Ч 10—6,2 = 10—6,6 =
aCa2+.
Для данного рассмотренного случая моляльность иона кальция в грунтовой воде оказалась исчезающе малой - всего несколько сотых частей на миллион. Такой порядок значений mCa2+, конечно, вполне правдоподобен. Если же фактический анализ воды покажет высокую концентрацию растворенного кальция, то это заставит предположить наличие каких-либо иных ионных или молекулярных компонентов раствора, содержащих кальций.
В сущности пятый случай - это комбинация первого и второго случаев, но вместе с тем он представляет и самостоятельный геологический интерес. Действительно, здесь отражается такое положение, когда дождевая вода - грубое подобие чистой воды, находящейся в равновесии с атмосферой,- просачивается вниз через пласт инертной почвы или горной породы и приходит в соприкосновение с породой, содержащей кальцит. Какое количество кар-боната будет выщелочено на единицу объема просочившегося раствора? Именно такой вопрос и встает при необходимости количественного определения выщелачивающей способности дождевых вод.
Здесь сохраняются те же основные уравнения равновесия, что и в предыдущих случаях, но несколько меняются характеристические уравнения. Сначала, при рассмотрении равновесия дождевой воды с атмосферой необходимы только те уравнения, которые отражают взаимоотношения растворенных карбонатных компонентов плюс уже известное значение атмосферного РCO2, и уравнение электрической нейтральности среды:
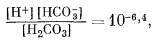 |
(3.2) |
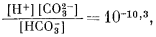 |
(3.3) |
| [H2CO3] = 10—1,5PCO2, | (3.17) |
| PCO2 = 10—3,5, | (3.26) |
| [H+] = [HCO—3] + 2[CO2—3] | (3.27) |
[расхождением значений mi и ai в уравнении (3.27) и в нижеследующем уравнении электронейтральности пренебрегаем].
Согласно уравнениям (3.26) и (3.17), [Н2СО3] = 10-5,0. Так как ионы Н+ образуются лишь в результате реакции СО2 с водой, концентрация карбонат-иона будет столь ничтожной (КHCO—3 = 10—10,3), что ею можно пренебречь. В связи с этим из уравнений (3.27) и (3.2) получаем
| [H+] = [HCO—3] | (3.27, видоизмененное) |
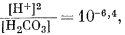 |
( подстановка в 3.2) |
| [H+]2 = 10—6,4 Ч 10—5,0 = 10—11,4, | |
| [H+] = 10—5,7, | |
| [HCO—3] = 10—5,7. | (3.27, видоизмененное) |
Отсюда определяем валовое содержание карбоната, растворенного в дождевой воде: [H2CO3] + [HCO—3] = 10—5,0 + 10—5,7 = 10—4,8. И в данном случае расхождение между активностями и моляльностями можно не учитывать, поскольку ионная сила такого раствора очень низка.
Когда дождевая вода приходит в контакт с кальцитом и вступает с ним во взаимодействие, первоначальная концентрация растворенных карбонатных компонентов увеличивается благодаря растворению кальцита. При этом каждый образующийся за счет кальцита карбонатный или бикарбонатный ион, как и молекулярная частица Н2СО3, образует один ион кальция:
| [Ca2+] + 10—4,8 = [H2CO3] + [HCO—3] + [CO2—3]. | (3.28) |
Согласно уравнению электрической нейтральности среды,
2[Ca2+] + [H+] = [HCO—3] + [OH+] + 2[CO2—3].
Для решения задачи необходимы и прочие соотношения:
| [Ca2+][CO2—3] = 10—8,3, | (3.1a) |
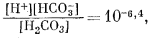 |
(3.2) |
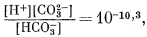 |
(3.3) |
| [H+][OH—] = 10—14,0. | (3.4a) |
Последующие расчеты аналогичны тем, которые были проведены при решении первого случая; они дают следующие результаты:
[Ca2+] = 10—3,85,
[H+]
= 10—9,9,
[H2CO3] =
10—7,5,
[HCO—3] =
10—4,0,
[CO2—3] = 10—4,4.
Любопытно, что эти величины лишь немного отличаются от соответствующих величин, вычисленных для первого случая, когда рассматривалось взаимодействие только между СаСО3 и Н2О, причем едва ли такое расхождение превышает возможную ошибку самого расчета. Действительно, растворимость кальцита увеличилась лишь на 10% по сравнению с его растворимостью в чистой воде. Как мы уже отмечали, валовое содержание карбоната в дождевой воде составляет всего 10—4,8 моль/л. Это обусловливает низкую реакционную способность дождевой воды и служит причиной близости значений концентрации для первого и пятого случаев. Однако, если в почве, через которую просачиваются дождевые воды, присутствуют корни растений или же имеются дополнительные источники CO2, растворимость кальцита увеличится, а равновесное значение рН станет ниже. Вместе с тем тот факт, что при взаимодействии дождевой воды с кальцитом создается довольно высокий рН, очевидно, не всегда должным образом учитывается при рассмотрении реакций в зоне выветривания.
И все-таки в заключение можно сказать, что роль растворенного CO2 в подземных водах, возможно, переоценивается и в то же время недооценивается влияние гидролиза и наличия CO2 в почвенной атмосфере.
Величина констант равновесия КH2CO3, KHCO—3 и КCaCo3 для рaзличных температур приведена в табл. 3.2. При расчетах карбонатных равновесии в системах с температурой, отличной от 25° С, безусловно, следует пользоваться значениями констант равновесия, соответствующими измеренной температуре. Изменение растворимости, происходящее в связи с изменением общего давления, становится существенным при давлении выше 25 атм; эта сторона проблемы будет рассмотрена в гл. 9.
Таблица 3.2
| Температура, °С | pK1a | pK2б | pKsв | pKCO2г |
| 0 | 6,58 | 10,62 | 8,02 | 1,12 (0,2°) |
| 5 | 6,52 | 10,56 | 8,09 | |
| 10 | 6,47 | 10,49 | 8,15 | |
| 15 | 6,42 | 10,43 | 8,22 | |
| 20 | 6,38 | 10,38 | 8,28 | |
| 25 | 6,35 | 10,33 | 8,34 | 1,47 |
| 30 | 6,33 | 10,29 | 8,40 | |
| 40 | 6,30 | 10,22 | 8,52 | 1,64 |
| 50 | 6,29 | 10,17 | 8,63 | |
| 80 | (6,32) | (10,12) | 8,98 | |
pK1
= -lgKН2СО3;
pK2 = -lgKHCO3;
pKs =
-lgKСаСО3;
pKCO2 =
-lgKCO2. | ||||
В природе карбонатные фазы редко встречаются в виде чистых соединений: для них характерно замещение одних элементов в катионной позиции другими. В какой степени следует учитывать подобные замещения при проведении расчетов равновесия с участием карбонатных минералов? Основа для решения этой проблемы была изложена в гл. 2; ниже для примера мы разберем конкретную систему с участием арагонита, в котором часть кальция замещена стронцием. В эти расчеты внесено лишь одно изменение, касающееся уравнения (3.1). Если соединение чистое, а активность твердого вещества равна единице, то при всех расчетах вводится упрощение, согласно которому [СаСО3] = 1. Но в случае катионных замещений активность твердого вещества меняется и в уравнение (3.1) вводится поправка на активность твердого вещества.
Стронциевый арагонит представляет собой двухкомпонентную систему. Следовательно, при описании соотношений между растворенными компонентами и твердыми веществами нам понадобятся два уравнения, соответствующих уравнению (3.1). Эти уравнения таковы:
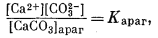 |
(3.29) |
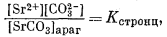 |
(3.30) |
где [CaCO3]арaг и [SrСО3]араг означают относительную активность СаСО3 и SrСО3 в "нечистом" арагоните. Если в простом случае с чистым карбонатом нас удовлетворяло уравнение (3.8), то теперь мы должны написать следующее равенство:
mCa2+ + mSr2+ = mCO2-3 + mHCO-3 + mH2CO3.
В связи с электрической нейтральностью системы уравнение (3.9) изменяем до выражения
2mCa2+ + 2mSr2+ + mH+ = 2mCO2-3 + mHCO-3 + mOH-.
Разделим уравнение (3.29) на уравнение (3.30) и после замены активностей на произведение коэффициентов активности и концентрации получаем
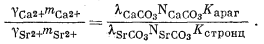 |
(3.31) |
Итак, для стронциевого арагонита известного состава расчет отношения концентраций Са2+ и Sr2+ в водном растворе возможен, если в распоряжении исследователя будут величины коэффициентов активности, участвующие в уравнении (3.31). Для таких разбавленных растворов, с которыми мы имеем дело, предположение о существовании приближенного равенства gCa2+ @ gSr2+ будет в достаточной степени осторожным. Воспользовавшись этим допущением и подставив численные значения констант равновесия для арагонита состава (Са0,95Sr0,05)CO3, по уравнению (3.31) находим
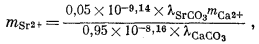 | |
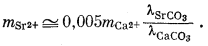 |
(3.32) |
Как было показано в гл. 2, величина коэффициента активности главного компонента, как правило, не отличается сколько-нибудь существенно от мольной доли главного компонента, так что в нашем примере можно предположить, что lCаСО3 @ 0,95. Величина же lSrСО3 в уравнении (3.32) нам остается неизвестной, однако, даже если допустить весьма значительное отклонение ее от единицы, все-таки можно полагать, что доля Sr2+ в общей растворимости арагонита будет небольшой. О соотношениях между l и N для случаев катионного замещения имеется мало данных, однако исследования в этом направлении быстро развиваются.
Итак, мы рассмотрели пять случаев, с которыми чаще всего сталкиваются геохимики при исследовании взаимоотношений карбонатов в природных водах, и остановились на методике решения подобных задач. В разобранных примерах использованы значения констант для 25° С. Все расчеты касались кальцита, но была сделана оговорка, что эта же методика применима в отношении карбонатов любых других металлов. Последний разобранный нами случай представлял собой комбинацию двух более простых случаев. На его примере мы показали, как огромное большинство сложных задач можно решить с помощью комбинации простых случаев. Для удобства приведены значения констант равновесия для температур, отличных от 25° С. Рассмотрена также методика решения задач с участием твердых растворов.
3.1. Какова растворимость
стронцианита (т. е. mSr2+) в природной воде в
равновесии с атмосферой (РCO2 =
10—3,5) при 25° С, если рН раствора равен 10, а ионная сила
0,10?
Ответ:
mSr2+ =
10—7,1.
3.2. Имеется карбонат
состава (Sr0,90Ca0,10) СО3 при 25° С в
природной воде, равновесной по отношению к атмосфере
(PCO2 = 10—3,5 атм);
допускается существование твердого раствора CaCO3 в
SrCO3.
а) Какова величина
ионного произведения [Са2+][СО2—3]?
Ответ: 10—9,35.
б) Какова
величина ионного произведения
[Sr2+][CO2—3]? Ответ:
10—9,20.
в) Определите
значение рН. Ответ: 8,1.
г) Какова
величина [Sr2+]? Ответ:
10—3,75.
д) Какова величина
[Са2+]? Ответ:
10—3,90.
3.3. Определите
растворимость кальцита при 50° С в растворе, рН которого равен 8, ионная
сила 0,10, а сумма растворенного CO2
(mH2СО3 +
mHCO—3 +
mCO2—3) составляет
10—3,0. (Следует допустить, что величина g не меняется с температурой.). Ответ:
mCa2+ =
10—2,9.
3.4. Какова
растворимость витерита в дождевой воде, открытой по отношению к атмосфере?
Определите равновесное значение
рН.
Ответ:
mBa2+ = 10—3,3; рН =
8,1.
3.5. Установлено, что проба морского
ила в ампуле равновесна по отношению к кальциту при рН = 7,5 (25° С).
Каково внутреннее давление СО2 в этой пробе? (Считайте, что
раствор в ампуле по составу первоначально соответствовал средней
приповерхностной морской воде.)
Ответ:
10—2,6 атм.
1. B a c k W. Geology and ground water features of the Smith River Plain, Del Norte County, California, U. S. Geol. Surv. Water-Supply Paper, 1254, 70, 1957.
2. H a r n e d H. S., В о n n e r P. T. Journ. Am. Chem. Soc., 67, 1026, 1945.
3. H a r n e d H. S., S с h о 1 e s S. R. Journ. Am. Chem. Soc., 63, 1706, 1941.
4. К e r n D. В. The hydration of carbon dioxide, Journ. Chem. Ed., 37, 14, 1960.
5. L a r s о n Т. Е., В u s w е 1 1 А. М. Journ. Аш. Water Works Assoc., 34, 1667, 1942.
6. M a r k a m А. А., К о b е К. А. Journ. Am. Chem. Soc., 63, 449, 1941.
С h a v е К. Е., D е f f е у е s К. S., W е у 1 Р. К., G а г г е 1 s R. М., Thompson М. Е. Observations on the solubility of skeletal carbonates in aqueous solutions, Science, 137, 33, 1962.
G a r r e l s R.M., T h o m p s o n M.E., S i e v e r R. Stability of some carbonates at 25° С and one atmosphere total pressure, Am. Journ. Sci., 258, 402, 1960.
H a r n e d H. S., В о n n e r F. T. The first ionization constant of carbonic acid in aqueous solutions of sodium chloride, Journ. Am. Chem. Soc., 67, 1026, 1945.
H a r n e d H. S., S с h о 1 e s S. R. The ionization constant of HCO—3 from 0-50°, Journ. Am. Chem. Soc., 63, 1706, 1941.
K e r n D. В. The hydration of carbon dioxide, Journ. Chem. Ed., 37, 14, 1960.
R e v е 1 1 e R., F a i r b r i d g e R. Carbonates and carbon dioxide, in Treatise on Marine-Ecology and Paleoecology, 1, Ecology, Gcol. Soc. Am. Memoir, 67, 239-295, 1957.
S c h o e l l e r H. Geochemie des eaux souterraines, Revue de 1'Institut Franc.ais du Petrole et Annales des Combustibles Liquides, Paris, 21-28, 1956.
S v e r d r u p H. U., M a r t i n W. J о h n s о n, F 1 e ш i n g R. H. The Oceans, New York, Prentice-Hall, 192-211, 1946.
T u r n e r R.C.A theoretical treatment of the рН of calcareous soils. Soil Sci., 86, 32, 1958.
|
|
|
|
[Содержание] [Глава 2] [Глава 4] |