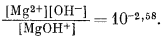
| Р.М. Гаррелс, Ч.Л. Крайст | Растворы, минералы, равновесия |
|
|
|
|
[Содержание] [Глава 3] [Глава 5] |
|
|
|
|
В настоящей главе мы детально рассмотрим одну из важнейших геохимических проблем - вопрос о действительной природе растворенных веществ в различных природных водах. Ранее, в гл. 2, в разделе о водных растворах электролитов, мы охарактеризовали различия, существующие между некоторыми классами электролитов, и дали определение ряду термодинамических параметров. Здесь будет продолжена эта тема, и поэтому мы советуем читателю прочесть гл. 2 заново.
В сильно разбавленных водных растворах, подобных водам большинства рек и озер, главные растворенные компоненты находятся в виде свободных ионов. Данные химического анализа такой воды, выраженные в концентрациях Na+, К+, Са2+, Mg2+, Cl-, S02-4, HСO-3 и т. д., представляют собой вполне удовлетворительную модель баланса компонентов раствора. По значениям концентраций таких компонентов и коэффициентам активности индивидуальных ионов, вычисленным на основе теории Дебая - Хюккеля или среднесолевым методом, o можно рассчитать активности этих компонентов с точностью до нескольких процентов.
По мере того как ионная сила раствора какой-либо одной соли приближается к 0,1 или становится еще выше, возрастают расхождения между значениями коэффициентов активности, рассчитанными по Дебаю - Хюккелю и среднесолевым методом. На фиг. 2.15 подобное расхождение видно, например, по быстрому отклонению кривой gNO-3 рассчитанной по экспериментальным значениям g±KCl и g±KNO3, от кривой, рассчитанной по методу Дебая - Хюккеля. В растворах смешанных электролитов, подобных морской воде (ионная сила 0,7), экспериментально определяемые коэффициенты активности ионов еще заметнее отклоняются от значений, которые следовало бы ожидать, исходя из расчетов по Дебаю - Хюккелю или по среднесолевому методу. Например, анализ фиг. 4.5 показывает, что для раствора КНСО3 при I = 0,7 величина gHCO-3 составляет 0,67, тогда как, согласно расчету, для морской воды она равна 0,47 [8].
Указанные выше расхождения можно объяснить дефицитом свободных ионов в растворе вследствие взаимодействия между тесно сближенными ионами, приводящего обычно к образованию ионных пар. Хотя возможны и иные толкования, здесь мы будем следовать представлению Бьеррума, согласно которому пара противоположно заряженных ионов, т. е. ионная пара, может рассматриваться как реальная термодинамическая единица в том случае, если она находится в равновесии с ионами, оставшимися свободными, и если это равновесие описывается термодинамической константой равновесия. Константа равновесия, выражаемая в виде либо константы ассоциации, либо противоположной ей константы диссоциации, является показателем доли недиссоциированной части растворенной соли в интересующем нас диапазоне концентраций. Ионные пары образованы кулоновским притяжением в отличие от существенно ковалентной связи в слабом электролите, например в слабой кислоте типа уксусной. Как уже указывалось в гл. 2, не всегда можно решить, состоит ли ассоциированный электролит из ионных пар или иных комплексов, но в нашем случае это различие, как правило, не играет существенной роли.
Для определения констант диссоциации ионных пар и комплексов иного типа применяются различные экспериментальные методы.
К ним относятся измерения проводимости, определения активности, измерения рН, спектрофотометрические исследования, кинетические измерения и другие методы. В каждом случае изучается поведение соли, а затем по характеру отклонения от поведения выбранного "стандарта" судят об ассоциации ионов в. виде тех или иных частиц. Один из обычно используемых стандартов - это КСl, который, как предполагают, полностью диссоциирует в растворе на простые ионы. В качестве стандарта используется и уравнение Дебая - Хюккеля в различных формах. Теория и экспериментальные методы определения констант диссоциации ионных пар более подробно изложены в работах Дэвиса [5, б].
Изучение всех возможных ионных пар, которые могут присутствовать в природной воде, содержащей много растворенных элементов, наталкивается на непреодолимые на первый взгляд трудности. Но если ограничить внимание элементами, которые составляют около 99% растворенного вещества в водах рек, озер, подземных вод и океанов, то окажется, что достаточно рассмотреть только десять элементов: Н, Na, К, Mg, Ca, Si, G1, О, S и С. Кроме того, можно полагать, что в растворе эти элементы находятся в виде хорошо известных ионов, радикалов или молекул: Н+, Na+, К+, Са2+ Mg2+, Н2СО3, HCO-3, С02-3, Сl-, S02-4, H4SiO4, H3SiO-4, а также в виде парных их комбинаций. Тогда для объяснения свойств данной природной воды мы, по-видимому, должны учитывать возможность образования в ней частиц, подобных NaCO-3, СаСО°3, MgHCO+3 или MgSO°4. Насколько известно, при низких температурах образование более сложных, чем ионные пары, комплексов с участием главных растворенных веществ не играет существенной роли в природных водах, исключая концентрированные рассолы.
В настоящее время, по существу, невозможно решить проблему определения активностей второстепенных составляющих природных вод, по крайней мере путем расчетов, основанных на анализах воды, ибо отсутствует достаточная информация о константах равновесия многих комплексов.
Коэффициенты активности свободных ионов, находящихся в равновесии с ионными парами, будут в основном зависеть от ионной силы раствора. Если предположить, что мы можем учесть все взаимодействия ближнего порядка, приводящие к образованию ионных пар и других комплексов (включая комплексы растворителя), то для определения коэффициентов активности нам достаточно рассмотреть лишь силы дальнего взаимодействия; следовательно, мы могли бы рассчитать эти коэффициенты с помощью теории Дебая - Хюккеля. Однако, как уже отмечалось выше, мы знаем далеко не все возможные взаимодействия в различных интересующих нас растворах. Как и следовало ожидать, для относительно разбавленных простых растворов расчеты по Дебаю - Хюккелю и по среднесолевому методу приводят к примерно одинаковым значениям коэффициентов активности ионов. В случае более концентрированных растворов для определения коэффициентов активности свободных ионов в основном применяется среднесолевой метод. Для некоторых заряженных ионных пар коэффициенты активности берутся по аналогии с частицами сходного типа, легче поддающимися измерениям. Ниже этот вопрос рассматривается более детально для особого случая, когда в качестве раствора фигурирует морская вода.
В растворе ионные пары могут составлять основную долю комплексов главных растворенных компонентов и значительную долю комплексов второстепенных компонентов. Константы диссоциации этих пар приведены в ряде работ. Из них наиболее полными являются книга Бьеррума, Шварценбаха и Силлена [2] по константам устойчивости комплексов с неорганическими лигандами, а также статья и книга Дэвиса [5, б]. В табл. 4.1 приведены константы диссоциации различных ионных пар и некоторых слабых электролитов типа HCO-3.
Таблица 4.1
| Катионы | Аниоиы | ||||
| ОН- | HCO-3 | CO2-3 | SO2-4 | С1- | |
| Отрицательные логарифмы констант диссоциации | |||||
| H+ | 14,0 | 6,4 | 10,33 | 2 | -a |
| К+ | - | - | - | 0,96 | - |
| Na+ | -0,7 | -0,25 | 1,27 | 0,72 | - |
| Са2+ | 1,30 | 1,26 | 3,2 | 2,31 | - |
| Mg2+ | 2,58 | 1,16 | 3,4 | 2,36 | - |
Индекс "а" обозначает
отсутствие поддающихся измерению ассоциации.
Пример:
MgOH+водн = Mg2+водн +
ОН-водн.
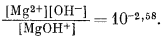
Метод предварительной оценки констант диссоциации некоторых еще детально не изученных растворенных компонентов изложен в работах Клиффорда [3, 4]. Этот автор показал, что графически зависимость pKsp = -lg (произведение активностей) от разности электроотрицательностей аниона и катиона для соединений какого-либо одного типа, например для ряда сульфидов одновалентных катионов Me2S, выражается прямой линией. Клиффорд применил график подобного типа к сульфидам, теллуридам, селенидам, гидроокислам и галогенидам. Следуя его примеру, мы построили график зависимости констант диссоциации от электроотрицательности катиона для различных ионных пар типа металл - гидроксил. Результаты показаны на фиг. 4.1. Их можно сравнить с соотношениями для произведений активности (произведений растворимости) твердых гидроокислов, изображенными на фиг. 4.2.
Электроотрицательность атома или группы атомов (с соответствующим зарядом) может быть определена как относительная энергия удаления электрона. Чем более несходен один вид атомов с другим, тем больше разность электроотрицательностей этих двух атомов. Например, F- приписывается электроотрицательность 4, a Na+ - электроотрицательность 1; разность между ними равна 3. Это означает, что связь Na+ и F- чрезвычайно полярна. В другом крайнем случае у двух атомов одного вида разность электроотрицательностей равна нулю, в связи с чем отсутствует и полярность в их химической связи. Например, в молекуле хлора Cl2 два атома хлора связаны по существу лишь одинарной ковалентной связью. Чем больше разница
 |
| Фиг. 4.1. Зависимость констант диссоциации растворенных
гидроокислов (выраженных в единицах pК = -lg К ) от
электроотрицательности катионов при 25° С. Величины К рассчитаны на основе значений DF°обр соответствующих компонентов; данные по электроотрицательности заимствованы у Гроуди и Томаса [И]. |
|
|
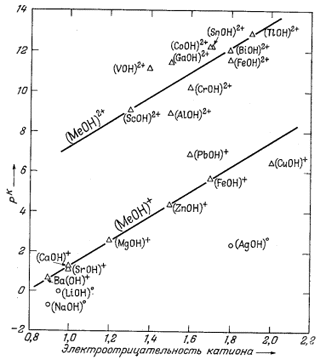
| Фиг. 4.2. Зависимость ионных произведений (произведений растворимости) твердых гидроокислов (выраженных в единицах pK = -lg К ) от электроотрицательности катионов при 25° С. Величины К получены тем же методом, что и для фиг. 4.1. |
в электроотрицательности между взаимодействующими ионами, тем больше доля кулоновского притяжения в химической связи получающегося комплекса. На фиг. 4.1 видно, что связи находящихся в растворе комплексов становятся более полярными, т. е. кулоновскими, при движении справа налево и, наоборот, более ковалентными - слева направо. Основные принципы электроотрицательности подробно рассмотрены Полингом [14].
На фиг. 4.1 заметно сильное рассеяние точек для комплексов с трехвалентными ионами, подобных Fe(OH)2+, но это вполне закономерно, так
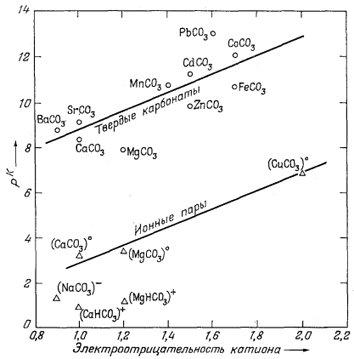 |
| Фиг. 4.3. Зависимость ионных произведении (произведений растворимости) твердых карбонатов (выраженных в единицах pK = -lg К ) и констант диссоциации растворенных ионных пар от электроотрицательности катионов при 25° С. Величины К получены тем же методом, что и для фиг. 4.1. |
как величины KMе(OH)2+ зависят от величин KMe(OH)3, которые с трудом определяются и сами обнаруживают разброс, как это видно на фиг. 4.2.
Фиг. 4.3 представляет собой график зависимости величин рК твердых карбонатов и констант диссоциации растворенных компонентов от электроотрицательности катиона. Для твердых веществ заметна общая тенденция возрастания pК с ростом электроотрицательности катиона. Однако отчетливо обнаруживается также и влияние размера катиона, так как точки карбонатов с меньшими катионами (Mg, Zn, Fe) отклоняются от средней линии в сторону более низких значений. В отношении констант диссоциации ионных пар карбонатов двухвалентных металлов существуют лишь разрозненные данные, и линия на графике проведена по трем точкам, для которых имеются данные.
Две точки - для Са(HCO3)+ и Mg(HCO3)+ - в настоящее время не поддаются интерпретации [10,13], хотя следует отметить, что эти две величины в значительной мере спорны вследствие большой ошибки определения соответствующих констант.
Константы диссоциации растворенных сульфатных комплексов и произведения растворимости твердых сульфатов совершенно отличны от констант диссоциации гидроокислов и карбонатов. График зависимости рК от электроотрицательности катионов не обнаруживает какой-либо закономерности. Однако между размером катиона и рК твердых сульфатов или константой диссоциации растворенных веществ ясно видна закономерная связь. На фиг. 4.4, которая и представляет собой такой график, заметно возрастание pK с увеличением размера катиона. В то же время величины рК ионных
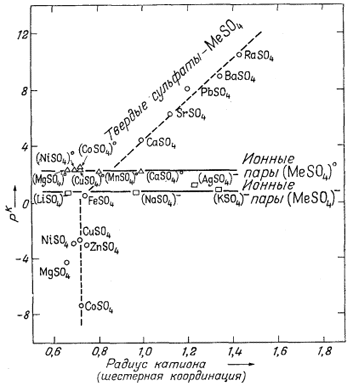 |
| Фиг. 4.4. Зависимость ионных произведении (произведений растворимости) кристаллических сульфатов (выраженных в единицах pК = -lg К) и констант диссоциации растворенных ионных пар от радиусов катионов (для шестерной координации в кристалле) при 25° С. Величины К рассчитаны на основе значений DF°обр; ионные радиусы - по Аренсу [I]. |
пар не зависят от размера катиона. Действительно, все показанные на графике ионные пары двухвалентных металлов типа MeSO°4 в растворе имеют примерно одинаковые рК (= 2,3). Аналогично этому все пары одновалентных металлов MeSO-4 также характеризуются примерно одинаковыми рK (= 0,8). Дело, вероятнее всего, в том, что ионная пара в растворе образуется в результате соединения гидратированного иона металла с сульфат-ионом, а поскольку все радиусы гидратированных ионов близки по размерам, то и силы связи между такими гидратированными катионами и сульфат-ионом могут оказаться близкими по величине.
При температуре земной поверхности с ионом хлора не взаимодействует в сколько-нибудь заметной степени ни один из главных катионов природных вод. Эта особенность может быть весьма полезна для геохимика, так как она означает, что приготовленные в лаборатории растворы, содержащие какой-либо один хлорид металла, можно использовать в качестве эталонных растворов для определения коэффициентов активности катионов даже при высоком значении ионной силы. Мы можем говорить об отсутствии комплексообразования применительно к щелочным и щелочноземельным металлам, однако это не относится ко многим другим элементам. Можно ожидать, что свинец, цинк, железо, марганец и др. взаимодействуют с ионом хлора и другими галогенами. Константы равновесия различных реакций с участием галогенид-ных комплексов металлов приведены в книге Бьеррума, Шварценбаха и Силлена [2].
Приводимые ниже рассуждения основаны на работе Гаррелса и Томпсона о химической модели морской воды [8].
В природных водах, менее концентрированных, чем морская, взаимодействие главных растворенных веществ, очевидно, выражено относительно слабо. Типичная речная вода, содержащая растворенные вещества в количестве нескольких сотен частей на миллион, имеет ионную силу порядка 0,01, а активности индивидуальных ионов в ней меньше 0,01. Например, если какая-либо речная вода содержит 40 ч. на млн. Са2+ и 61 ч. на млн. HCO-3, моляльности обоих ионов равны 0,001, а их активности еще меньше. Согласно табл. 4.1, константа диссоциации CaHCO+3 равна 10-1,26. В первом приближении
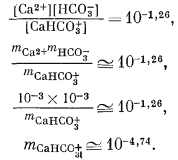
Использование активностей Са2+ и HCO-3 даст даже меньшую величину активности СаНСО; во всяком случае, в виде СаНСО+3 будет связано самое большее несколько процентов ионов кальция и бикарбоната. Подобные расчеты для других возможных взаимодействий между главными растворенными компонентами дают аналогичные результаты.
Ионная сила морской воды равна 0,7, т. е. концентрация растворенных в ней солей достаточно велика, и между присутствующими ионами происходит заметное взаимодействие, существенно изменяющее термодинамические свойства раствора. В табл. 4.2 приведен средний состав приповерхностной морской воды при 25° С. Указанные в ней ионы составляют по меньшей мере 99,7% общего количества растворенных твердых веществ.
Таблица 4.2
| Ион | Моляльность | Ион | Моляльность | Ион | Моляльность |
| Na+ | 0,48 | К+ | 0,010 | НСО-3 | 0,0024 |
| Mg2+ | 0,054 | Cl- | 0,56 | С02-3 | 0,00027 |
| Са2+ | 0,010 | S02-4 | 0,028 |
Анализ таблицы констант диссоциации (табл. 4.1) показывает, что не нужно принимать во внимание комплексов каких-либо катионов с ионом хлора или К+ с ионами НСО-3 или СO2-3. Однако К+ взаимодействует с сульфатом, a Na+, Ca2+ и Mg2+ с SO2-4, HCO-3 и СО2-3 (взаимодействием с ОН- можно пренебречь ввиду низкой концентрации ОН-). Если учесть все эти данные, то к преобладающим компонентам, растворенным в морской воде, можно отнести К+, KSO-4, Na+, NaCO-3, NaHCO°3, NaSO-4, Ca2+, СаНСО+3, СаСО°3, CaSO°4, Mg2+, MgHCO+3, MgCO°3, MgSO°4, HCO-3, CO2-3, SO2-4 и Cl- - всего 18 форм.
Чтобы найти распределение этих форм, требуется 18 независимых уравнений. В нашем распоряжении имеются два вида информации: соотношения баланса масс, т. е.
mK+ + mKSO-4 = mK+общ,
и уравнения констант диссоциации, т. е.
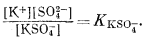
Для совместного использования обоих видов информации требуется знать коэффициенты активности для перевода моляльностей в активности и наоборот. Предположим, что нам известны все виды индивидуальных растворенных частиц в морской воде. Тогда мы еще должны знать величины коэффициентов активности таких нейтральных соединений, как CaSO°4, MgSO°4 и т. д., различных свободных (некомплексированных) ионов, Na+, К+, Сl-, СО2-3 и т. д., и таких ионных пар, как NaCO-3, КSО-4.
Величины индивидуальных коэффициентов активности, приводимые ниже для различных компонентов, соответствуют раствору с ионной силой морской воды, которая принята за 0,71 (стр.96).
Н е з а р я ж е н н ы е к о м п о н е н т ы. Какие-либо данные о коэффициентах активности таких нейтральных ионных пар, как CaSO°4, MgSO°4, CaCO°3 и NaHCO°3, в настоящее время отсутствуют. По-видимому, эти соединения вряд ли ведут себя в водном растворе электролитов подобно растворенным газам; другими словами, очень трудно подыскать им аналоги. Вероятно, проще всего принять, что коэффициенты активности этих соединений равны единице. Такое допущение не должно существенно влиять на конечные результаты, поскольку в расчеты, где используются эти коэффициенты, входят различные неопределенные величины.
З а р я ж е н н ы
е к о м п о н е н т ы. Коэффициенты
активности индивидуальных ионов для К+ и С1-
определяются по среднему коэффициенту активности КСl; при этом
предполагается, что gK+ =
gCl- = g±KCl. Измерение активности К+
стеклянным электродом по методике, описанной в гл. 8, дает величину,
хорошо согласующуюся с расчетным значением по g±KCl. Сходным образом величины gNа+ получаются из g±NaCl и g±KCl. И в этом случае измерения
чувствительным к натрию стеклянным электродом
|
1 (стр.96) Точнее говоря, ионная сила может быть рассчитана только методом последовательных приближений после учета комплексообразования. Но так как общая степень комплексообразования мала и имеются существенные расхождения в величинах различных используемых констант, любые поправки к величине ионной силы, полученные путем таких расчетов, не имеют большого значения. |
контролируют величину, установленную среднесолевым методом, с точностью в пределах 2%.
Коэффициенты активности НСО-3 и СO2-3 берутся из нанесенных на фиг. 4.5 данных для растворов КНСО3 и К2СО3 соответственно. Считается также, что коэффициенты активности NaCO-3, MgHCO+3, CaHCO+3, KSO-4 и NaSO-4 равны коэффициенту активности НСО-3. По-видимому, близкие значения характерны для всех однозарядных частиц примерно такого же размера.
Величины gCa2+ и gMg2+ получаются при использовании значений g± соответствующих хлоридов совместно с величиной g±KCl. В растворах CaCl2 и MgCl2 при 25° С комплексообразования, очевидно, не происходит.
С коэффициентом активности SO2-4 связаны особые трудности. Все соответствующие соли, для которых имеются данные по средним коэффициентам активности, обнаруживают значительное комплексообразование при ионных силах, сравнимых с ионной силой морской воды. Однако, используя упомянутые выше величины gK+ и gKSO-4, константу диссоциации KSO-4 и значения g± для K2SO4, можно рассчитать gSO2-4 как функцию ионной силы.
Таблица 4.3
| Растворенные компоненты |
Коэффициент активности | Метод нахождения |
| NaHCO°3 | 1,13 | Аналогия с H2CO3 |
| MgCO°3 | 1,13 | То же |
| CaCO°3 | 1,13 | " " |
| MgSO°4 | 1,13 | " " |
| CaSO°4 | 1,13 | " " |
| НСО-3 | 0,68 | Фиг. 4.5, кривая А |
| NaCO-3 | 0,68 | Аналогия с НСО-3 |
| NaSO-4 | 0,68 | То же |
| KSO-4 | 0,68 | " " |
| MgHCO+3 | 0,68 | " " |
| CaHCO+3 | 0,68 | " " |
| NA+ | 0,76 | Измерение стеклянным электродом |
| K+ | 0,64 | gK+ = g±KCl |
| Mg2+ | 0,36 | gMg2+ = (g3±MgCl2)/(g2±KCl) |
| Ca2+ | 0,28 | gCa2+ = (g3±CaCl2)/(g2±KCl) |
| Cl- | 0,64 | gCl- = g±KCl |
| C02-3 | 0,20 | Фиг. 4.5, кривая D |
| S02-4 | 0,12 | См. Текст |
|
1 (стр.97) Значения коэффициентов активности, указанные в табл. 4.3, взяты из работы Гаррелса и Томпсона [8]. Однако значения, принятые для нейтральных и заряженных ионных пар, как и для индивидуальных ионов, до некоторой степени спорны, поскольку невозможно указать точные пределы ошибок для этих величин. Чтобы показать степень их надежности, вероятно, лучше всего привести различные максимально отличающиеся друг от друга значения, предполагавшиеся для этих величин. Гаррелс и Томпсон принимали 1,13 для незаряженных частиц, причем допускалось, что истинное значение может быть на один или несколько процентов ниже. Для gMg2+ они приняли 0,36, т. е. значение, полученное на основе определенного ряда опубликованных для 'У+]У["С] данных; другой серии данных соответствует gMg2+ = 0,29. Для gNа+ измерения стеклянным электродом давали 0,76, а расчеты на основе опубликованных данных для g±NаСl дают 0,71. Указанные расхождения соответствуют, по-видимому, максимально допустимым ошибкам. |
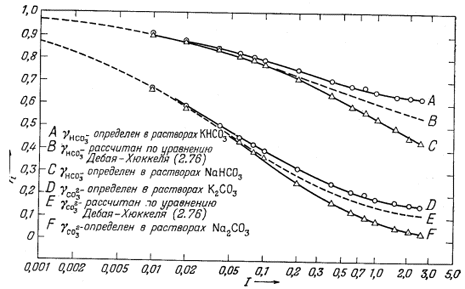 |
| Фиг. 4.5. Коэффициенты активности ионов бикарбоната и
карбоната. Кривые А, С, D и F нанесены по экспериментальным данным Уокера, Брэя и Джонстона [16], кривые В и Е рассчитаны по, уравнению Дебая-Хюккеля (2.76). |
В табл. 4.3 сведены значения коэффициентов активности индивидуальных ионов с указанием методов, использованных для нахождения каждой величины.
Чтобы определить моляльность различных компонентов, предположительно присутствующих в морской воде, нужно составить уравнение баланса масс для одного из анализируемых компонентов и использовать его в сочетании с уравнениями констант диссоциации, учитывающими эти компоненты. Аналитически установленная величина концентрации SO2-4 обозначена символом mSO2-4 o6щ.; она может быть приравнена к сумме концентраций различных компонентов, содержащих сульфат-ион:
| mSO2-4 общ = mNaSO-4 + mKSO-4 + mCaSO°4 + mMgSO°4 + mSO2-4 свободн. | (4.1) |
Вместе с тем должны быть справедливы следующие соотношения равновесной диссоциации различных компонентов:
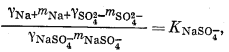 |
(4.2) |
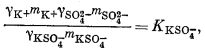 |
(4.3) |
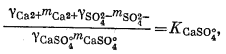 |
(4.4) |
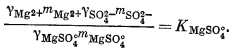 |
(4.5) |
Таким образом, для описания различных сульфатных форм имеется пять уравнений. Однако, даже если известны mSO2-4 o6щ. и все значения К и g, этого еще недостаточно, так как мы имеем еще девять неизвестных (моляльности содержащих SO2-4 компонентов плюс моляльности ионов Na+, К+, Са2+ и Mg2+, поскольку эти последние могут входить в другие комплексы).
Один из путей решения задачи заключается в следующем. Нужно написать уравнение баланса масс для компонентов, содержащих СO2-3, и выражения их констант диссоциации, а также уравнение баланса масс для компонентов, содержащих НСО-3, плюс выражения их констант диссоциации. Тогда возможно совместное решение полученных уравнений с помощью вычислительной машины, как это было продемонстрировано Хелгесоном [12].
Достаточно быстрый способ решения задачи без применения счетного устройства основан на предположении незначительного комплексообразования катионов Na+, К+, Са2+ и Mg2+, т. е. на том, что
mNa + общ = mNa + свободн и т. д.
Это предположение приемлемо, потому что заряд катионов в морской воде балансируется главным образом зарядом иона хлора и общая моляльность катионов намного превышает моляльность комплексообразующих ионов SO2-4, CO2-3 и НСО-3. В таком случае число неизвестных в уравнениях (4.1) - (4.5) уменьшается на четыре и уравнения могут быть решены относительно моляльностей различных сульфатных компонентов. Решение уравнений подтверждает начальное предположение, согласно которому в комплексы связаны лишь небольшая часть Ca2+ и Mg2+ и совершенно незначительные доли Na+ и К2+.
С помощью подобных допущений и таким же методом можно рассчитать моляльности комплексов, содержащих НСО-3 и СО2-3. Наконец, вся задача решается второй раз путем введения поправок к моляльностям Ca2+ и Mg2+ на количества этих ионов, связанные в комплексы с SO2-4, HCO-3 и СO2-3. Достаточно одного такого пересчета, чтобы получить результаты с точностью, лежащей в пределах точности различных других численных величин, используемых в расчетах. (Если предположение о незначительном комплексировании катионов содержало серьезную ошибку, для удовлетворительного решения всех уравнений может потребоваться несколько пересчетов.)
Результаты расчетов показаны в табл. 4.4.
Таблица 4.4
| Ион | Моляльность (общая) |
Свободные ионы, % | Пара Me-S04, % | Пара Ме-НСО3, % | Пара Ме-СО3. % | |
| Na+ | 0,48 | 99 | 1+ | |||
| К+ | 0,010 | 99 | 1 | - | - | |
| Mg2+ | 0,054 | 87 | 11 | 1 | 0,3 | |
| Са2+ | 0,010 | 91 | 8 | 1 | 0,2 | |
| Ион | Моляльность (общая) |
Свободные ионы, % | Пара Ca-анион, % | Пара Mg-анион,% | Пара Na-анион, % | Пара К-анион,% |
| S02-4 | 0,028 | 54 | 3 | 22 | 21 | 0,5 |
| НСО-3 | 0,0024 | 69 | 4 | 19 | 8 | - |
| СО2-3 | 0,00027 | 9 | 7 | 67 | 17 | - |
| С1- | 0,56 | 100 | - | - | - | - |
Пытаясь представить себе свойства проанализированного вещества, мы подсознательно используем ту форму, в которой выражены результаты химического анализа. Это случается даже тогда, когда мы вполне сознаем, что информация обманчива. Результаты анализов изверженных пород представляются в виде содержаний окислов. Почти нет сомнений в том, что, размышляя относительно природы магм, которые являются в значительной мере ионными, исследователи сталкиваются с трудностью мысленного перехода от окислов к ионам. В случае модели морской воды аналитические
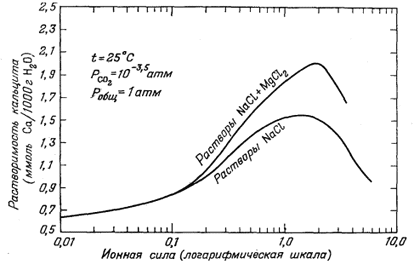 |
| Фиг. 4.6. Рассчитанная зависимость растворимости кальцита от ионной силы в растворах NaCl и NaCl + MgCl2 (для NaCl и MgCl2 принято отношение их количеств, типичное для морской воды) [9]. |
результаты значительно лучше передают природу среды, но связанные с комплексообразованием усложнения, показанные в табл. 4.4, полезны для понимания многочисленных явлений химии морской воды.
Предложенная модель не производит заметных изменений в картине состояния главных катионов. Они, очевидно, присутствуют в растворе в основном в виде индивидуальных свободных ионов. Имеется лишь небольшое количество ионных пар с SO2-4, особенно у Са2+ и Mg2+. Но возрастание концентрации SO2-4 в морской воде (например, при испарении) вызовет возрастание доли этих катионов, связанной в CaSO°4 или MgSO°4. Заметим также, что почти постоянная максимальная величина активности этих ионных пар достигается в том случае, когда раствор находится в равновесии с твердыми сульфатами.
Осаждение гипса в равновесных условиях из концентрированной морской воды можно выразить следующими уравнениями:
| CaSO4 Ч 2H2Oкрист = CaSO°4 водн + 2H2Oжидк, | (4.6) |
| [CaSO°4][H2O]2= Kгипс, | |
| CaSO°4 водн = Ca2+водн + SO2-4 водн, | |
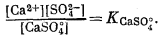 |
(4.7) |
При постоянной активности воды активность СаSО°4 также постоянна.
Основное изменение в наших представлениях, основанное на только что выведенной химической модели морской воды, касается анионов SO2-4, НСО-3 и СO2-3. В комплексы типа ионных пар с катионами связано более 30% ионов SO2-4 и НСОO-3 и 90% всего СОO2-3. Выяснение степени комплексообразования СОO2-3 и природы его комплексов полезно для тех, кто пытается разгадать тайны отложения различных карбонатных минералов, составляющих столь важную часть геологической летописи. Ранее при объяснении причины осаждения СаСО3 обычно рассматривали соотношения только между СОO2-3 и Н+; ныне стало очевидным,что содержание Mg2+ и Na+ в морской воде почти так же важно для осаждения СаСО3, как и содержание Н+. Например, организм, который выделяет Mg2+ из своей клеточной жидкости, способствует отложению СаСО3 в связи с разрушением комплексов Mg2+ с СОO2-3. Бесспорно, что в водах океана краткосрочные вариации концентрации у Н+, как правило, шире, чем у Mg2+ или Nа+, но в течение геологического времени коренные изменения в растворимости СаСО3 могли быть вызваны изменением содержаний Mg2+ и Na+. Это соображение иллюстрируется фиг. 4.6, на которой показана растворимость кальцита при постоянном давлении СО2 и постоянной температуре в растворах NaCl и NaCl + MgCl2.
При изменении температуры,
давления и состава воды распределение компонентов будет меняться по
сравнению с распределением в обычной морской воде при 25° С и общем
давлении, равном 1 атм. Количественная оценка влияния давления и
температуры приводится в одной из последующих глав. Качественно же
рассмотренная выше картина распределения довольно хорошо выдерживается в
пределах тех вариаций температуры и давления, которым подвержены воды
океана.
Обработка данных путем расчетов, основанных на ионных равновесиях, очень трудна в случае природных водных сред, более концентрированных, чем морская вода. Если в морской воде главные растворенные компоненты представлены свободными ионами или ионными парами, то в концентрированном природном рассоле степень взаимодействия между растворенными веществами выше; здесь образуются формы, более сложные, чем ионные пары.
Лишь немногие типы природных вод достаточно просты по составу, чтобы мы могли приблизиться к выявлению форм, присутствующих в растворе. В табл. 4.5а приведен частный химический анализ рассола из озера Дип-Спрингс, Калифорния1 (стр.101) . Распределение компонентов, рассчитанное методами, аналогичными использованным для морской воды, показано в табл. 4.5б, а степени комплексообразования различных веществ - в табл. 4.5в.
В этот расчет необходимо
ввести дополнительную ступень. Как показывает табл. 4.56, в рассоле по
существу не остается двухвалентных анионов; все они расходуются на
взаимодействие с катионами, образуя незаряженные или однозарядные
компоненты. Поэтому в первоначальную величину ионной силы рассола,
рассчитанную по данным химического анализа, следует ввести поправку. Для
морской воды изменение ионной силы вследствие образования ионных пар
несущественно, но для рассола первоначальное значение ионной силы,
вычисленное по данным химических анализов, примерно вдвое больше величины,
получающейся после введения поправки
|
1 (стр.101) Анализ любезно предоставлен Б. Джонесом (Отдел водных ресурсов Геологической службы США). |
| Ион | Частей на 1 млн. | Моляльность2 (стр.102) |
| Na+ | 101000 | 6,48 |
| К+ | 15700 | 0,59 |
| С02-3 | 63300 | 1,56 |
| HCO-3 | 12500 | 0,30 |
| SO2-4 | 40500 | 0,62 |
| С1- | 58100 | 2,42 |
| Сумма 291 100 | 11,97 |
|
1 Сумма растворенных твердых веществ 322 000. 2 (стр.102) Ионная сила, основанная на данных в анализе компонентах, равна 9,26. |
Таблица 4.6б
| Ион | Моляль- ность1 |
Коэффи- циент- активно- сти |
Актив- ность |
Ион | Моляльность | Коэффи- циент- активно- сти |
Актив- ность |
| Na+ | 3,50 | 1,17 | 4,10 | К+ | 0,50 | 0,59 | 0,30 |
| NaCO-3 | 0,69 | 0,60 | 0,41 | KSO-4 | 0,09 | 0,60 | 0,054 |
| NaSO-4 | 0,37 | 0,60 | 0,22 | SO2-4 | 0,15 | 0,11 | 0,016 |
| NaCO03 | 0,84 | 1,88 | 1,58 | Cl- | 2,42 | 0,59 | 1,43 |
| NaHCO° | 0,20 | 1,88 | 0,38 | ||||
| НСО-3 | 0,10 | 0,60 | 0,06 | Сумма | 9,06 | ||
| CO2-3 | 0,20 | 0,11 | 0,02 |
|
1 Ионная сила 4,5. |
Таблица 4.5в
| Ион | Общая моляль- ность/моляль- ность свободного иона |
Комплексообра- зование, % |
Ион | Общая моляль- ность/моляль- ность свободного иона |
Комплексообра- зование, % |
| Na+ | 6,48/3,50 | 46 | НСО-3 | 0,30/0,10 | 67 |
| К+ | 0,59/0,50 | 15 | SO2-4 | 0,62/0,15 | 76 |
| СO2-3 | 1,56/0,20 | 87 | Cl- | 2,42/2,42 | 0 |
на уменьшение количества заряженных частиц, вызванное взаимодействием ионов.
Значительная роль взаимодействия растворенных частиц, наблюдаемая в концентрированных солевых растворах, указывает на столь заметные различия в химизме рассолов и разбавленных поверхностных или грунтовых вод, что, вероятно, правильнее считать эти различия качественными, а не просто количественными.
Попытки рассчитать растворимость минералов в рассолах в настоящее время почти безнадежны из-за того, что на нее влияет растворимость ряда компонентов с неизвестными константами диссоциации. Даже если бы были известны все виды взаимодействий, пришлось бы решать систему с очень большим числом уравнений. Однако результаты, полученные, быть может, после многочасовых расчетов, все равно окажутся далеко не точными из-за суммирования ошибок определения различных констант диссоциации, коэффициентов активности отдельных ионов, ионной силы и тому подобных величин.
Средняя вода открытого океана с ионной силой 0,7 по концентрации растворенных веществ, по-видимому, примерно соответствует верхнему пределу для таких природных вод, применительно к которым детальная обработка данных на основе теоретических расчетов и результатов химических анализов еще имеет какой-то смысл.
Значительно более
перспективный метод решения вопросов, связанных с термодинамическими
свойствами природных водных растворов, заключается в использовании
химических анализов воды и прямых измерений актив-ностей индивидуальных
ионов посредством чувствительных к ионам электродов (гл. 8). Таким путем
можно избежать сложностей расчета активностей ионов с использованием
констант диссоциации, коэффициентов активности индивидуальных ионов и
ионной силы.
До сих пор еще никто не
пытался обобщить все данные о комплексных ионах с участием 90
второстепенных элементов, присутствующих в природных водах. В связи с этим
приводимые ниже сведения отрывочны и неполны, и самое большее, что мы
может сделать на данном этапе, это высказать предположения о некоторых
взаимоотношениях, еще требующих исследования и систематизации.
Трехвалентные катионы, например Fe3+, V3+, Аl3+, Сr3+, Мn3+ и т. п., обычно отмечаются в природных водах в весьма низких концентрациях, за исключением редких вод с высокой кислотностью. Поскольку это небольшие по размерам ионы с высоким зарядом, у них проявляется тенденция не только активно взаимодействовать почти со всеми анионами, давая растворимые комплексы, но и образовывать нерастворимые гидроокислы в значительной части диапазона рН природных вод. Как хорошо видно на фиг. 4.1 и 4.2, твердые гидроокислы имеют высокие значения pК. Поэтому, хотя трехвалентные ионы и являются сильными комплексообразователями, их общая растворимость все же остается низкой из-за появления труднорастворимых окислов и гидроокислов. Можно вообще сказать, что если установлена измеримая концентрация трехвалентного иона, то в растворе имеется какой-то комплекс или группа комплексов. Большие значения рК ионов (МеОН)2+ на фиг. 4.1 указывают на существование сильного взаимодействия трехвалентных ионов с ОН-, приводящего к образованию растворимых форм. Трехвалентные ионы взаимодействуют также с анионами галогенов, сульфата и, вероятно, бикарбоната и карбоната, хотя в двух последних случаях изучение равновесии затрудняется крайне низкой растворимостью других соединений.
В кислой области свободные трехвалентные ионы, как правило, сохраняются лишь в необычных условиях высокой кислотности и низкой ионной силы. При постепенной нейтрализации трехвалентные ионы связываются в комплексы с ОН- и осаждаются в виде нерастворимых гидроокислов. При высоких значениях рН иногда образуются анионные комплексы с ОН- тина FеО-2 [или Fe(OH)-4 без 2Н2О], но величины рН, необходимые для обеспечения измеримой растворимости трехвалентных ионов в форме анионов, обычно выходят за интересующие геологов пределы. Заметным исключением, имеющим геологическое значение, является ион АlO-2, который может обусловить существенную растворимость алюминия в растворе с необычным, но не слишком высоким рН.
Таким образом, аналитически
определяемые трехвалентные ионы при низких рН, вероятно, находятся в
растворе в форме катионных комплексов, в то время как при высоких рН они
входят преимущественно в состав анионных гидроксильных комплексов.
Один лишь тот факт, что для этого раздела использовано заглавие "Двухвалентные катионы" без подзаголовков для щелочных земель, переходных металлов и т. д., говорит о малочисленности имеющихся данных. Поведение Са2+ и Mg2+ в какой-то степени уже было разобрано (рассматривалась их роль как главных катионов природных вод). Как показывает линейная зависимость на фиг. 4.1, у двухвалентных катионов тенденция к ассоциации усиливается с ростом электроотрицательности, т. е. с возрастанием доли ковалентной связи. Следовательно, комплексы с ОН-, S2-, Se2- и галогенами (исключая F-) в общем будут слабыми у щелочноземельных металлов, но более устойчивыми у переходных и следующих за ними металлов.
Большой интерес для специалистов по минеральным месторождениям представляет то обстоятельство, что чем больше величина рК для произведения растворимости ковалентного соединения, например сульфида, тем больше величина рК для константы диссоциации аналогичного ему растворенного комплекса. Это означает, что ионная ассоциация в растворе стремится вызвать большее относительное возрастание растворимости слабо растворимого сульфида, чем умеренно растворимого. Поэтому при возрастании ионной силы наблюдается тенденция не только к увеличению растворимости соединений, подобных сульфидам, но также и к выравниванию их раствори-мостей. Исследователи рудных месторождений давно знают, что концентрации различных металлов в определенных рудоносных растворах должны быть приблизительно равны, даже если их растворимости, выраженные через концентрации одних свободных ионов металлов, различаются на несколько порядков.
В целом по степени
возрастания ассоциации в смешанных природных растворах электролитов
двухвалентные ионы, вероятно, располагаются в такой последовательности: Ва
< Sr < Са (см. фиг. 4.1-4.3). С этим общим правилом, как отмечалось
ранее, не согласуется поведение сульфатных комплексов. При высоком
содержании сульфата в растворе наблюдается тенденция к пропорциональному
увеличению растворимости всех сульфатов металлов в связи с тем, что все
константы диссоциации сульфатов Me2+ близки к
10-2,3.
Катионы с зарядами 4+ и выше в общем ведут себя одинаково; различие в их поведении связано лишь с одной особенностью, имеющей большое геологическое значение. Маленькие ионы с высокими зарядами имеют такое сродство к кислороду, что превращаются в устойчивые анионные комплексы: силикаты, перманганаты, ванадаты, ванадиты, хроматы, молибдаты, вольф-раматы и т. д.
Общие особенности поведения металл-анионных комплексов хорошо иллюстрируются поведением пятивалентного ванадия. В очень кислых растворах (рН < 2) V5+ присутствует в виде катионного комплекса VO+2, а в сильно щелочных (рН @ 14?) - в форме ортованадат-иона VO3-4. При медленном подкислении щелочного раствора происходит ряд превращений посредством реакций с участием Н+ и H2O:
| 2VO3-4 + 2H+
Ортованадат (бесцветный) |
= |
V2O4-7 +
H2O Пированадат (бесцветный) |
(pH @ 13), |
| 5V4O4-12
+ 8H+ |
= |
2V10O6-28 +
4H2O Поливанадат (оранжевый) |
(pH @ 6,5), |
| V10O6-28
+ H+ |
= |
HV10O5-28 Гидрополиванадат (оранжевый) |
(pH @ 6), |
| HV10O5-28 +
H+ |
= |
H2V10O4-28 Дигидрополиванадат (темно-оранжевый) |
(pH @ 4), |
| H2V10O4-28 +
4H+ + 2H2O |
= |
5V2O5 Ч H2O Гидрат пятиокиси ванадия (твердый, темно-коричневый) |
(pH @ 2,5), |
| V2O5 Ч H2O + 2H+ | = |
2VO+2 +
2H2O Перванадил (светло-желтый) |
(pH @ 1,5), |
Таким образом, при изменении среды от щелочной к кислой осуществляется серия последовательных превращений от простого иона (VO3-4) через ряд все более высоко полимеризованных ионов до образования нерастворимого окисла и, наконец, до перехода снова в раствор в виде кислородсодержащего катиона VO+2. Реакции образования полимеров медленны, но обратные реакции еще медленнее. Так что в лабораторных условиях, взяв за основу кислые растворы и нейтрализуя их, по существу невозможно достичь равновесия между различными формами ванадатов.
В целом простые ванадаты щелочных металлов растворимы довольно хорошо, а ванадаты двухвалентных ионов - значительно хуже. Однако, за исключением некоторых соединений типа карнотита (уранилванадата калия) со смешанными катионами, ванадаты лишь в редких случаях устойчивы в природных условиях.
Другие соли кислородных
кислот, такие, как молибдаты, вольфраматы и силикаты, ведут себя в
растворах сходным образом, отличаясь в основном величиной рН, необходимой
для образования простых ортоионов; рН, при котором образуются
нерастворимые окислы или гидроокислы; и диапазоном , рН, в котором
устойчивы эти окислы и гидроокислы. Молибден образует полимолибдаты в
нейтральных, а группу сложных гидроокислов - в более кислых условиях.
Довольно низкий рН, необходимый для растворения этих окислов до катионов,
в природных условиях не достигается. Химия кремнезема в природных
растворах при низких температурах упрощается благодаря тому, что полиионы
образуются только в сильно щелочных растворах (рН і 9), и в большинстве природных вод встречается лишь
простой нейтральный мономер H4SiO4, а величины рН,
достаточно низкие для образования катиона типа
НSiO+2, не наблюдаются.
При 25° С у одновалентных
катионов тенденция к образованию комплексов выражена очень слабо, хотя она
может стать важным фактором в высоко-концентрированных рассолах. Ион
калия, исключая его поведение в сульфатных растворах, удивительно
"благороден", что указывает на практическое отсутствие ассоциаций с
галогенами, бикарбонатом, карбонатом, бисульфидом и сульфидом. Ион натрия,
напротив, более склонен к взаимодействию; при благоприятных условиях он
может участвовать в комплексообразовании, создавая ионные пары с
ОН-, НСО-3 и
СOO2-3, а также с SO2-4. Так,
можно показать, что в крепких растворах Na2CO3,
например в водах некоторых содовых озер, имеется значительная концентрация
недиссоциированного Na2CO°31. В воде, насыщенной
Na2CO3 (общая моляльность около 2,5), около 30% этой
растворенной соли находится в виде Na2CO°3 и столько
же - в форме NaCO3. О поведении других одновалентных ионов
лучше всего судить по неполным данным и намечающимся закономерностям,
показанным на фиг. 4.1-4.4.
Многие рассмотренный выше
положения иллюстрируются фиг. 4.7, на которой изображена зависимость
логарифма отношения количества элемента в морской воде к общему количеству
этого элемента, попадающему в океан в результате выветривания пород, от
отношения заряда катиона элемента к его радиусу (ионного потенциала).
Величина, отложенная по ординате, соответствует выраженной одним из
способов растворимости; значение, отложенное по абсциссе, является грубой
мерой тенденции катиона к связи с анионами. Диаграмма указывает на уже
рассмотренные общие тенденции и многие специфические отклонения от этих
тенденций. Следует обратить внимание на такие особенности: относительно
высокую растворимость соединений типичных одновалентных катионов, например
щелочных металлов; относительно высокую растворимость щелочных земель;
более низкие растворимости меньших по размеру двухзарядных катионов,
образующих ряд слабо растворимых соединений с различными анионами;
исчезающе малую растворимость соединений с трехвалентными ионами, легко
возникающими в различных природных процессах, например с ионами железа,
алюминия и кобальта. Такие трехвалентные ионы, несмотря на склонность к
образованию растворимых комплексов, мало переходят в раствор, так как
осаждаются в виде окислов и гидроокислов. Наконец, у тех элементов,
которые дают небольшие катионы высокой валентности, взаимодействующие с
кислородом с образованием анионов металл - кислород, вновь наблюдается
тенденция роста растворимости. Можно считать в самом общем виде, что
нерас-
|
1 Неопубликованные эксперименты Гаррелса и Томпсона, Гарвардский университет. |
творимые окислы и гидроокислы трехвалентных и некоторых четырехвалентных катионов характеризуются минимумом растворимости при обычно
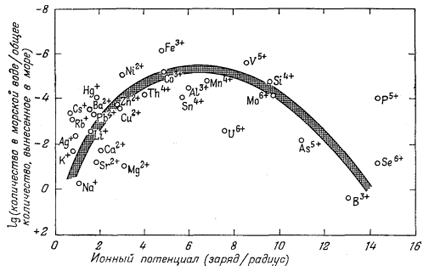 |
| Фиг. 4.7. Диаграмма зависимости между ионными потенциалами катионов и логарифмом отношения общего количества элемента в морской воде к общему количеству того же элемента, вынесенному, согласно расчетам, в океаны в результате выветривания пород. Ионные радиусы по Аренсу [I], данные о распространенности олементов по Ран-каме и Сахаме [15]. |
встречающихся величинах рН, тогда как некоторые четырехвалентные катионы и катионы с более высокой валентностью обнаруживают минимум растворимости в сильно кислых условиях, но проявляют тенденцию переходить в раствор в форме окси-полиионов в нейтральных или щелочных условиях.
Таблица 4.6
| Комплекс | Константа диссоциации | Концентрация аниона в растворе |
Отно- шение комп- лекс/ про- стой кати- он |
Концентрация аниона в растворе |
Отно- шение комп- лекс/ про- стой кати- он |
| Сu(СО3)2-2 водн | 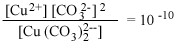 |
[СO2-3] = 10-5 | 100 | [CO2-3] = 10-1 | 108 |
| СuСО03 водн | 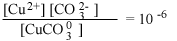 |
[CO2-3] = 10-5 | 101 | [CO2-3] = 10-1 | 105 |
| UO2(СО3)4-3 водн | 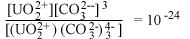 |
[СO2-3] = 10-10 | 10-6 | [СO2-3] = 10-6 | 106 |
| РbСl+водн | 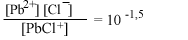 |
[Сl-] = 10-3 | 10-1,5 | [Сl-] =100 | 101,5 |
| СdI2-4 водн | 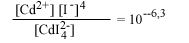 |
[I-] = 10-2 | 10-1,7 | [I-] = 100 | 106,3 |
| CuS-5 водн | 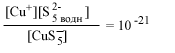 |
[S2-5] = 10-21 | 100 | [S2-5] = 10-10 | 1011 |
В табл. 4.6 авторы
предприняли попытку показать несколько взаимодействий, которые могут иметь
место между второстепенными катионами и обычными анионами природных вод.
Данные таблицы свидетельствуют об огромном влиянии замены
комплексообразующего аниона на активность свободного иона металла,
особенно если комплекс содержит более одного аниона.
Образование комплексов в водных растворах при повышенных температурах детально было рассмотрено Хелгесоном [121. Следующий раздел в значительной степени является кратким изложением части его работы.
Данные по константам диссоциации комплексных ионов при повышенных температурах все еще слишком отрывочны для надежных обобщений, касающихся изменения устойчивости комплексов с температурой. Однако гипотетическое рассмотрение влияния температуры и давления на водные солевые растворы позволяет прийти к полезным выводам относительно условий, при которых образование комплексов будет тормозиться или, наоборот, стимулироваться.
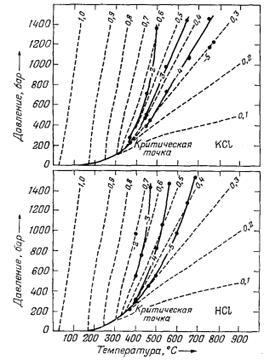 |
| Фиг. 4.8. Диаграммы температура - давление - плотность для воды,
на которые сплошными линиями нанесены изолинии логарифмов констант
диссоциации КСl (верхняя диаграмма) и НСl (нижняя). Штриховые линии - изолинии плотности воды. Заметьте, что у изолиний lg К и плотности наблюдается тенденция к взаимной параллельности и что величины lg К уменьшаются с понижением плотности воды [12] |
Если раствор нагревается при почти постоянной плотности, то кинетическая энергия молекул воды возрастает, но, так как среднее расстояние между ионами растворенных веществ и молекулами воды не изменяется, степень гидратации растворенных компонентов стремится остаться такой же, как при комнатной температуре. Поэтому можно было бы ожидать, что зависящая от гидратации степень ассоциации ион - ион в данном растворе не должна заметно меняться с температурой, если плотность остается постоянной. С другой стороны, если раствор нагревается со значительным расширением, ди-польные молекулы воды больше не собираются так плотно вокруг растворенных ионов, и их полярные эффекты - основная причина высокой степени ионизации солей в воде - заметно уменьшаются. Тогда тенденция ионов типа Na+ и С1- соединяться в таком растворе с образованием NaCl будет усиливаться. На фиг. 4.8 показаны соотношения давление - температура - плотность для воды, а также нанесены изолинии констант диссоциации КСl и НСl. Изолинии констант диссоциации почти параллельны соответствующим изолиниям плотности. По данным Франка [7], подобное поведение наблюдается у LiCl, NaCl, RbCl, CsCl, КОН и HF.
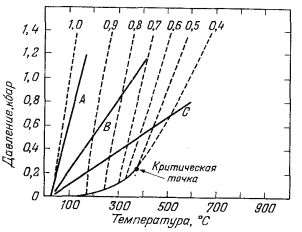 |
| Фиг. 4.9. График соотношений температура - давление - плотность
для воды с нанесенными на него линиями трех соотношений глубины и
температуры, типичных для земной коры. Градиент А соответствует литостатическому давлению и нормальному температурному гра диенту; градиент В - гидростатической нагрузке и нормальному температурному градиенту; градиент С - гидростатическому давлению и аномальному температурному градиенту. Штриховыми линиями показаны изолиния плотности воды. |
На фиг. 4.9 три типичных геотермических градиента нанесены на график давление - температура - плотность для воды. Градиент А соответствует условиям в поровых водах, подвергающихся литостатическому давлению пород с плотностью 2,5 г/см3 при типичном "нормальном" геотермическом градиенте 1° С на 100 футов (~ 30 м). Так как в этом случае плотность поровых вод почти постоянна, трудно ожидать коренных изменений в степени ассоциации электролитов. Градиент В является "нормальным" гидростатическим градиентом при том же геотермическом градиенте 1°С на 100 футов (~ 30 м). В этих условиях на некоторой глубине плотность воды будет несколько меньшей, чем в первом случае, и комплексообразование должно возрастать по сравнению с комплек-сообразованием при градиенте А.
Градиент С отвечает аномально высокому геотермическому градиенту и представляет собой первое приближение к условиям температуры и давления, которые могут встретиться между поверхностью и неглубоко залегающей магмой. Заметьте, что этот резкий градиент пересекает больше изолиний плотности на единицу давления, чем градиенты А или В.
С полным основанием можно предположить, что в условиях геосинклинального осадкообразования геотермический градиент занимает какое-то промежуточное положение между градиентами А и В; плотность поровых вод должна быть очень высока, и распределение растворенных компонентов между свободными ионами и комплексами не должно заметно изменяться. Иными словами, вода в геосинклинальных условиях даже на глубине во многом подобна воде на земной поверхности: она является высоко полярным растворителем. С другой стороны, любое возрастание термического градиента выше нормального, возможно, вызванное интрузивным телом на небольшой глубине, заметно уменьшает плотность воды. Поэтому вода начинает терять свой типично полярный характер, и происходит ассоциация растворенных компонентов. Таким образом, высокотемпературные водные растворы низкой плотности совершенно не похожи на низкотемпературные плотные жидкости, с которыми мы чаще всего имеем дело. Отношение магмы к сосуществующей водной фазе несколько сходно с отношением водного солевого раствора к сосуществующему органическому растворителю при комнатной температуре. Магма растворяет вещества в ионной форме, а сосуществующая вода стремится растворить их в молекулярной. При 600° С и плотности воды 0,4 г/см3 НСl, NaCl и КСl почти полностью ассоциированы в водном растворе (Kдисс = 10-4 - 10-6). Такое поведение поразительно контрастирует с их "полной" диссоциацией при комнатной температуре.
Хотя представленная здесь качественная картина и обрисовывает характер главных изменений, которые следует ожидать с возрастанием тепературы, все же при попытках предсказать поведение конкретных компонентов возникают серьезные затруднения. Не подлежит сомнению, что в случае простой диссоциации соли типа NaCl уменьшение полярных эффектов растворяющей воды будет способствовать усилению ассоциации частиц. Однако что можно сказать о компонентах типа РbСl2-4? Устойчив ли он в сильно полярной среде в большей степени, чем составляющие его индивидуальные ионы? Устойчив ли он более чем PbCl-3? Ответ зависит от тонких различий в отношении таких компонентов и индивидуальных ионов к окружающим их диполям воды.
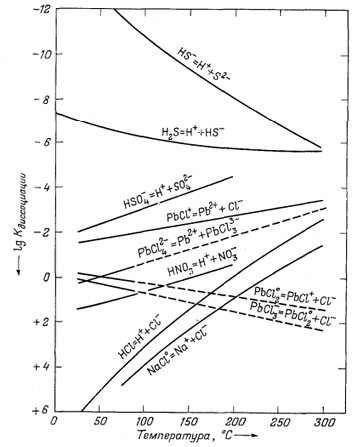 |
| Фиг. 4.10. Зависимость констант диссоциации различных компонентов раствора от температуры. Составлено по данным Хелгесона [12]. |
Фиг. 4.10 показывает
температурную зависимость констант диссоциации ряда компонентов и в общем
демонстрирует разнообразие их поведения. Заметьте, однако, что величины
Кдисс для большинства ионных пар уменьшаются с ростом
температуры.
Природные воды представляют собой многокомпонентные 'растворы электролитов. В настоящее время имеется химическая информация, достаточная для расчета взаимодействий между главными растворенными компонентами при температурах земной поверхности в средах с такой же концентрацией, как у морской воды (ионная сила 0,7). Рассмотрена полезная для расчетов модель, основанная на том предположении, что более концентрированные растворы отличаются от очень разбавленных вод с "полной" ионизацией лишь возникновением новых компонентов, состоящих не более чем из пары тех компонентов, которые существовали при сильном разбавлении. Для решения большинства интересующих нас вопросов концепция "полной" ионизации главных компонентов, растворенных в природных водах, при ионной силе ниже примерно 0,05, по-видимому, не нуждается в усовершенствовании. При более высоких значениях наблюдается усиление взаимодействия, и можно считать, что в морской воде большой процент карбонатов, бикарбонатов и сульфатов образует ионные пары с катионами. В плотных рассолах взаимодействие проявляется достаточно широко и следует принимать во внимание комплексные частицы более высоких порядков, чем ионные пары. Взаимодействие является настолько сильным, что для некоторых рассолов эффективная ионная сила составляет, вероятно, лишь около половины ионной силы, рассчитанной в предположении полной диссоциации.
Если изменения плотности воды с ростом температуры невелики, то влияние температуры на внутреннюю структуру водных растворов, по-видимому, относительно мало. Вообще же уменьшение плотности с возрастанием температуры стремится вызвать ассоциацию индивидуальных ионов, так что при высокой температуре и малой плотности даже галогениды щелочей и неорганические кислоты и основания представляют собой слабые электролиты.
Необходимы дальнейшие
работы, прежде чем мы сможем произвести достаточно обоснованные расчеты
взаимодействий второстепенных составляющих природных вод.
4.1. Если рК
диссоциации MgCO°3 равен 3,4, чему равно отношение активности
СO2-3 к MgCO°3 в растворе, в котором
активность Mg2+ равна 10-2,1? Ответ:
10-1,3.
4.2. Раствор,
содержащий 0,01 моль NaHCO3 в 1000 г
Н2О, имеет рН 8,4 при 25°
С.
а) Чему равно отношение активности
иона карбоната к активности
бикарбоната?
б) Какие растворенные
компоненты нужно учитывать при рассмотрении внутренних равновесии такого
раствора?
в) Чему равна ионная сила
раствора, если считать, что NaHCO3 полностью диссоциирован на
Na+ и HCO-3 и каких-либо иных ионов не
образует?
г) Если предполагать полную
диссоциацию, как в случае (в), то чему равны gNa+ и gHCO-3 по теории Дебая
- Хюккеля?
д) Каково уравнение баланса
масс для содержащих Na+ компонентов в 0,01 М растворе
NaHCO3 при учете различных известных растворенных
компонентов?
Ответ: а)
10-1,93; б) Na+, NaHCO°3,
NaCO°3, HCO-3,
СО2-3, Н+, Н2СО3;
в) I = 0,01; г) gNa+
= 0,90, gHCO-3 =
0,90; д) mNa общ = mNa своб +
mNa HCO°3 +
mNaCO-3 =
0,01.
4.3. Рассчитайте распределение
растворенных компонентов в 0,1 М растворе NaHCO3 при 25°
С, используя уравнения баланса масс, константы диссоциации и коэффициенты
активности; рН раствора равно 8,4.
Ответ:
mNa+своб @ 0,095,
mNaHCO°3 @ 0,003,
mNaCO-3 @
0,002, mH2CO3 @ 0,001, mCO2-3
@ 0,002,
mHCO-3 @
0,092.
1. A h r e n s L. H. Geochim. et Cosmochim. Acta, 2, 155,
1952.
2. B j e r r u m J.,S c h w a r z e n b a c h G., S i l l e n
L.G. Stability Constants, Part II, Inorganic Ligands, London, The Chemical
Society, 1958.
3. C l i f f o r d A. F. Journ. Am. Chem. Soc.,
79, 5404, 1957.
4. C l i f f o r d А. F. Journ. Phys. Chem.,
63, 1227, 1959.
5. D a v i e s C. Incomplete dissociation in
aqueous salt solutions. In The Structure of Electrolytic Solutions, Walter
J. Hamer (ed.), New York, Wiley, 19-34, 1959.
6. D a v i e s C. Ion
Association, Washington, D. C., Butterworth, 1962.
7. F r a n c k E. U.
Angew. Chemie, 73, 309, 1961.
8. G a r г e 1 s R. M., T h о m p
s о n M. E. Am. Journ. Sci., 260, 57, 1962.
9. G a г r e 1 s R.
M., T h о m p s о n M. E., S i e v e r R. Control of carbonate solubi lity
by carbonate complexes, Am. Journ. ScL, 259, 43, 1961.
10. G r e
e n w a l d I. The dissociation of calcium and magnesium with bicarbonate,
Journ. Phys. Chem., 67, 720, 1963.
11. G r о d у W., T h o m a s
W. J. 0. Electronegativities of the elements, Journ. Chem. Phys.,
24, 439, 1956.
12. H e 1 g e s о n H. C. Complexing and
Hydrothermal Ore Deposition, New York, Per-gamon, 38-59, 1964.
13. H о
s t e 11 e r P. B. Complexing of magnesium with bicarbonate, Journ. Phys.
Chem., 67, 720, 1963.
14. P a u l i n g L. The Nature of the
Chemical Bond, 3rd ed., Ithaca, New York, Cornell, 88-107, 1960.
15. R
a n k a m а К., S a h a m a Th. G. Geochemistry, Chicago III, The
University of Chicago Press, 295, 1950.
16. W a 1 k e r А. С., В r а у
U. В., J о h n s t о n J. Journ. Am. Chem. Soc., 49, 1255, 1927.
B j e r r u m J.,S c h w a r z e n b a c h G., S i 11 ё n
L.,G. Stability Constants, Part II, Inorganic Ligands, London, The
Chemical Society, 1958.
D a v i e s C. W. Ion Association, Washington,
D. C., Butterworth, 1962.
H a m e r W. J. (e d.). The Structure of
Electrolytic Solutions, New York, Wiley, 1959.
H e l g e s o n H.C.
Complexing and Hydrothermal Ore Deposition, New York, Pergamon, 1964.
P
a r s o n s R. Handbook of Electrochemical Constants, London, Butterworth,
1959.
|
|
|
|
[Содержание] [Глава 3] [Глава 5] |