Глава 7. Диаграммы Eh-рН

В последнее время отмечается весьма ощутимый прогресс в использовании диаграмм Eh - рН при изображении полей устойчивости минералов. Это и не удивительно, поскольку составляющие, необходимые для их построения, известны уже в течение многих лет. Развитие наших представлений о рН и его широкое использование при интерпретации химических превращений в почвах и природных водах насчитывает несколько десятилетий. Уравнение Нернста, выражающее зависимость Eh от Е°, а также от активности реагирующих веществ и продуктов реакций, выведено еще раньше.

Мы не имеем возможности привести сколько-нибудь полный список интересных для геолога работ, в которых были бы существенным образом использованы Eh, или рН, или оба эти показателя вместе. Несмотря на это, постараемся осветить развитие метода изображения устойчивости минералов, ссылаясь лишь на некоторые основные работы (они даны в хронологическом порядке). Еще в 1923 г. Кларк [1] подробно рассмотрел взаимозависимость Eh и рН, но его интересы ограничивались только областью биохимии. Так как все внимание Кларка было приковано к равновесиям между растворенными компонентами, а не твердыми веществами, то для геохимиков исследования Кларка дали мало полезных сведений.

Одной из первых статей, посвященных соотношениям устойчивости минералов, явилась статья В. В. Щербины [9] о роли окислительного потенциала при образовании минеральных парагенезисов. Однако, рассматривая влияние рН, автор указанной статьи не построил графиков с использованием в качестве переменных Eh и рН. Вместе с тем он выделил группы минералов, которые могут сосуществовать в данных условиях Eh среды.

Следующей вехой был выход в свет классического труда Зобелла о величинах Eh морских осадков [8]. В этой работе, опубликованной в широко распространенном геологическом журнале, даны исчерпывающий разбор теории и практики измерения Eh и рН, а также интерпретация результатов измерений в природных средах. Статья охватывает более широкий круг вопросов, чем указано в ее заглавии, так как содержит критический обзор большинства предыдущих исследований. Единственное, что в ней отсутствует, это изображение полей устойчивости твердых веществ в виде функции Eh и рН. Работа Зобелла, а также статья Старки и Уайта [б], вышедшая годом ранее, стали основным руководством для каждого, кто в своей работе использует величины рН и Eh.

В дальнейшем привлекла к себе внимание работа Мейсона [4], в которой рассматривалась зависимость соотношения устойчивости минералов от Eh и рН среды. Однако и этот автор не привел сколько-нибудь четких диаграмм, отражающих поля устойчивости минералов.

В 1946 г. Пурбэ опубликовал книгу по термодинамике разбавленных растворов [5], которая в 1949 г. была переведена на английский язык. Из-за своего скромного названия эта работа вначале не была замечена геохимиками, хотя излагаемые в ней методы идеально подходили для расчета равновесии между минералами. В 1953 г. авторы написали статью, касающуюся соотношении устойчивости в зависимости от Eh и рН, однако но решились опубликовать ее, не ознакомившись детально с работой Пурбэ. Книга Пурбэ явилась итогом десятилетних исканий в области развития методики графического изображения устойчивости твердых веществ и растворенных компонентов как функции Eh и рН. В дальнейшем почти все исследователи опирались на данные Пурбэ и лишь незначительно изменяли или усовершенствовали предложенные им методы.

Со времени выхода в свет своей книги Пурбэ - директор Бельгийского центра по изучению коррозии - опубликовал в соавторстве со своими сотрудниками большое число технических отчетов, каждый из которых касался равновесных условий для какого-либо элемента в воде, содержащей растворенный кислород. Эти отчеты представляют для нас большой интерес, и в конце данной главы мы приводим их полный список. Поскольку чистые химические вещества близки к минералам, содержащиеся в отчетах данные могут быть без исправлений использованы всеми, кто интересуется соотношениями устойчивости минералов, хотя указанные отчеты прежде всего предназначены для металлургов.

Именно благодаря тому толчку, который дали работы Пурбэ, диаграммы Eh - рН-устойчивости быстро вошли в практику геохимических исследований. Библиографический список некоторых опубликованных Пурбэ работ, представляющих интерес для геологов, будет приведен в гл. 11.

ПОСТРОЕНИЕ ДИАГРАММ Eh - рН

Технику построения диаграмм Eh - рН мы подробно рассмотрим на примере исследования соотношений между минералами железа. Детальность предлагаемых расчетов, которая в применении к одним только соединениям железа не нужна, оправдывается надеждой на то, что читатель сможет при желании использовать подобные расчеты для соединений других элементов. Затруднения, которые при этом могут встретиться, лучше всего будут освещены в том случае, если все стороны расчетов для железа будут проведены с необходимой основательностью.

Определения и методы измерения Eh и рН детально рассматривались в гл. 5. Там было показано, что для любой окислительно-восстановительной системы можно написать уравнение полуреакции:

Восстановленное состояние = окисленное состояние + nе,

(5.23)

в котором множитель п означает число электронов, участвующих в данной полуреакции. Соответствующий потенциал полуэлемента определяется следующим уравнением:

(5.24)

Здесь Eh - потенциал полуэлемента, измеренный относительно стандартного водородного электрода; Е° - стандартный потенциал полуэлемента, т. с. напряжение на полуэлементе, когда активности всех компонентов, участвующих в полуреакции, равны единице.

Для полуреакции, протекающей по схеме

aA + bB = cC + dD + ne,

уравнение (5.24) устанавливает, что при 25° С

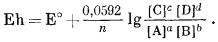
Это уравнение вместе с фундаментальным соотношением, определяемым уравнением (1.22), Е° = DF°_{реакции}/(nБ), дает ту основу, на которой построены последующие наши расчеты.

Все предлагаемые вычисления проделаны для 25° С и 1 атм общего давления; активности чистых твердых веществ и чистых жидкостей приняты равными единице, а активность газовой фазы приравнена к ее давлению. В заключение будет рассмотрено влияние небольших отклонений температуры и давления от 25° С и 1 атм.

УСТОЙЧИВОСТЬ ВОДЫ

В гл. 6 на основании константы равновесия для реакции

2Н₂О_жидк = 2Н_{2 газ} + O_{2 газ}

устойчивость воды была выражена в виде функции парциальных давлений водорода и кислорода.

Верхний предел устойчивости воды определялся равновесием между водой и кислородом при давлении 1 атм. Эти соотношения изображены на фиг. 6.1.

Если мы захотим показать те же пределы в виде функции Eh и (или) рН, то должны написать реакцию между водой и кислородом, выраженную через водородные ионы и (или) электроны, и таким образом получить возможность изображения полученных соотношений на графике, осями координат которого будут служить Eh и рН. , Для верхнего предела устойчивости воды, т. е. при Р_O2 = 1 атм,

2Н20жидк = 02 газ + 4Н+водн + 4е.

(7.1)

Тогда по уравнению (5.24)

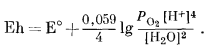(7.2)

При наших условиях Р_O2 = 1 и активность чистой воды в жидком состоянии тоже равна единице; тогда уравнение (7.2) упрощается:

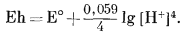Подставляя -рН вместо [Н⁺], получаем

Eh = E° - 0,059pH.

(7.3)

Следовательно, равновесие между водой и кислородом, парциальное давление которого равно 1 атм, выражается на графике Eh - рН прямой линией с наклоном -0,059 в на единицу рН и проходит через точку Е°. Чтобы получить численное значение Е° для данной реакции, определяем стандартную свободную энергию и подставляем ее в уравнение (1.22):

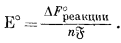(1.22)

Сначала подсчитываем величину DF°_{реакции}:

2Н20жидк = 02 газ + 4Н+водн + 4е.	(7.1)
DF°обр О2 + 4DF°обр H+ - 2DF°обр H2O = DF°реакции,
0 + (4 ґ 0) - 2 ґ (- 56,69) = +113,4 ккал.

Подставив это значение в уравнение (1.22), получим

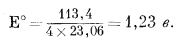Окончательно уравнение примет следующий вид:

Eh = l,23 - 0,059pH.

(7.4)

Линия, отражающая это соотношение, показана на фиг. 7.1. Заметим, что данная линия должна характеризовать постоянное давление кислорода. По существу отличие между изображением рассматриваемого соотношения

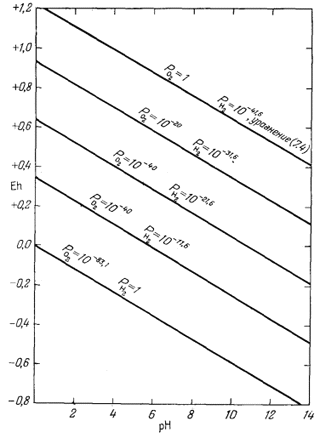Фиг. 7.1. Пределы устойчивости воды, выраженные в виде функции Eh и рН при 25° С и 1 атм общего давления. При промежуточных значениях Eh парциальные давления водорода и кислорода указаны в изолиниях.

в виде функции Р_O2 и в виде функции Eh и рН заключается в том, что вместо одной переменной мы берем две. Вообще говоря, такая практика противоречит правилу, согласно которому в расчетах обычно максимально уменьшают количество переменных величин. Однако Eh и рН легко измеряются; кроме того, во многих наших рассуждениях фигурируют выражения "кислотность и щелочность", "восстановление и окисление". Поэтому такое изображение реакций представляется весьма полезным.

Если мы вновь обратимся к уравнению (7.2), то увидим, что его можно переписать с учетом полученного значения Е°:

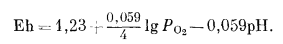(7.5)

При парциальном давлении кислорода, равном 1 аmм, величина Р_O2 сокращается, но очевидно, что с помощью этого уравнения на диаграмме Eh - рН можно построить линию для любого заданного парциального давления кислорода. Отсюда же следует, что изобары кислорода на диаграмме Eh - рН (в равновесии с водой) будут представлены прямыми параллельными линиями с наклоном -0,059 в/рН.

Кроме того, на основании соотношения, вытекающего из уравнения (6.1):

2Н2Ожидк = 2Н2 газ + O2 газ,

парциальное давление водорода при любом заданном Р_O2 также будет постоянной величиной. Отсюда заключаем, что линии Р_H2 должны быть прямыми и иметь тот же наклон, что и линии Р_O2 Вместе с тем значения Р_H2 можно получить и другим путем. Напишем полуреакцию

H2 газ = 2Н+водн + 2е.

(7.6)

В этой полуреакции не участвует жидкая вода, но ее присутствие подразумевается выражением Н⁺_водн. Уравнение для Eh будет иметь следующий вид:

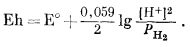Подставив -рН вместо lg [H⁺] и сделав небольшое преобразование, получим

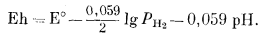(7.7)

Как и ранее, численное значение Е° определяем, рассчитав DF°_{реакции} и подставив полученную величину в уравнение

E°реакции = DF°реакции/nБ : 2DF°обр H+ - 2DF°обр H2 = DF°реакции,

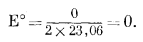Поскольку Е° = 0, окончательное уравнение примет следующий вид:

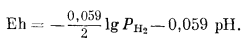(7.8)

Фиг. 7.1 представляет собой графическое изображение уравнений (7.5) и (7.8). Самая верхняя и самая нижняя прямые линии отвечают условиям, при которых или Р_O2 = 1 атм, или Р_H2 = 1 атм. Таким образом, эти линии показывают пределы равновесного существования воды в условиях земной поверхности или в близповерхностных средах.

В лабораторных условиях вода может длительное время существовать при более низких и более высоких значениях Eh. Чтобы вода начала заметно разлагаться, обычно необходимо превышение Eh на 0,5 в. Однако реакция разложения воды может идти и быстрее, чему, в частности, активно способствуют бактерии. Отсюда представляется маловероятным, чтобы природные воды могли долго сохранять Eh, величина которого выходила бы далеко за пределы границ, указанных на фиг. 7.1.

УСТОЙЧИВОСТЬ ОКИСЛОВ ЖЕЛЕЗА

Как следует из гл. 6, к стабильным фазам железа относятся самородное железо, магнетит и гематит. Соотношения устойчивости этих соединений там были определены в виде функции парциального давления кислорода. Полученные соотношения можно преобразовать и выразить в виде функции Eh и рН, для чего к реакциям железа с кислородом следует добавить полуэлементную реакцию разложения воды. Тогда реакция окисления железа до магнетита изменится следующим образом:

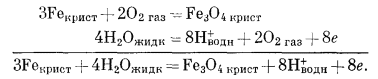(6.10) (7.1) (7.9)

Это сложение позволяет исключить из суммарной реакции газообразный кислород, а вместо него подставить в качестве переменных Н⁺ и электроны.

Стандартная свободная энергия реакции (7.9) равна

DF°обр Fe3O4 + 8DF°обр H+ - 3DF°обр Fe - 4DF°обр H2O = DF°реакции
- 242,4 + (8 ґ 0) - (3 ґ 0) - 4 ґ (-56,69) = -15,6 ккал

На основании уравнения

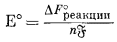Реакцию полуэлемента, соответствующую реакции (7.9), теперь можно выразить уравнением Eh:

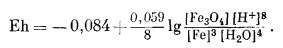(7.10)

Учитывая, что активности Fe₃O_{4 криcт}, Fe_криcт и Н₂О_жидк равны единице (если вода почти чистая!), пишем

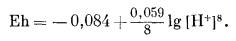Подставив -рН вместо lg [H⁺], найдем

Eh = -0,084 - 0,059 рН.

(7.11)

Следовательно, реакция между железом и магнетитом на диаграмме Eh - рН может быть выражена прямой линией, которая будет иметь тот же наклон, что и линии, характеризующие границы устойчивости воды.

Вывод уравнения Eh - рН для окисления магнетита до гематита аналогичен только что рассмотренному; приведем его без каких-либо пояснений:

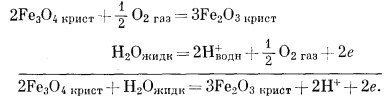	(6.14) (7.1) (7.12)
3DF°обр Fe2O3 + 2DF°обр H+ - 2DF°обр Fe3O4 - DF°обр H2O = DF°реакции,
3 ґ (-177,1) + (2ґ0) - 2 ґ (-242,4) - (-56,69) = +10,2 ккал,
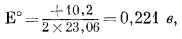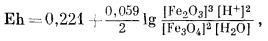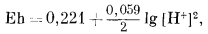Eh = 0,221 - 0,059 pH.	(7.13)

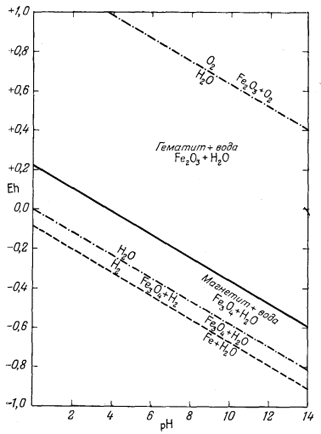
Согласно уравнению (7.13), граница между полями устойчивости магнетита и гематита параллельна линии железо - магнетит. На фиг. 7.2 графически изображены уравнения (7.11) и (7.13); там же показана граница устойчивости воды. Линия, отвечающая реакции Fe - Fe₃O₄, лежит ниже нижней границы устойчивости воды; поэтому в присутствии воды равновесие между Fe и Fe₃O₄ не может сохраняться. Другими словами, рассматривая соотношения между окислами железа с точки зрения их восстановления - отметим, что магнетит будет устойчив вплоть до нижнего предела устойчивости воды, т. е. до того момента, когда вода начнет разлагаться, чтобы прийти в равновесие с водородом, парциальное давление которого равно 1 атм. Поэтому поле устойчивости железа в присутствии воды не может быть достигнуто без нарушения равновесия. Таким образом, проведенная на диаграмме линия отвечает границе устойчивости между железом и магнетитом при том условии, что присутствующая жидкая вода метастабильна.

На фиг. 7.3 подведены итоги описания соотношений устойчивости окислов железа и воды, выраженных в виде функции Eh и рН. В дальнейшем эта диаграмма будет использована как основа для определения характеристических ионных активностей.

СООТНОШЕНИЯ УСТОЙЧИВОСТИ ГИДРООКИСЛОВ ЖЕЛЕЗА

При осаждении железа из растворов его солей путем добавления едкой щелочи прежде всего в осадок выпадает водный окисел железа с неопределенным содержанием воды, который часто относят к гидрату окид трехвалентного железа. Этот первый из выпадающих осадков неустойчивых отношению как к гематиту, так и гётиту.

Соотношения между свежеосажденным "гидратом окиси железа" и гематитом мы можем выразить следующим образом:

2Fe(ОН)3 осажденный = Fe2O3 криcт + ЗН2Ожидк.

(7.14)

Активности реагирующих веществ и продуктов реакции равны единице, в связи с чем эта реакция относится к типу "либо идущей - либо неидущей".

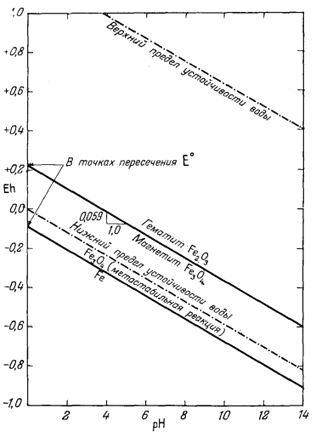Фиг. 7.2 Границы между железом и магнетитом и между магнетитом и гематитом в виде функции Eh и pH при 25° С и 1 атм общего давления. Поскольку граница Fe-Fe3O4 находится под нижним пределом устойчивости воды, то соответствующая реакция метастабильна. Металлическое железо в присутствии воды не может устойчиво существовать при любых значениях pH.

Фиг. 7.3 Поля устойчивости окислов железа, выраженные в виде функции Eh и pH при 25° С и 1 атм общего давления. Штриховая линия - нижний предел устойчивости магнетита в присутствии метастабильной воды.

По данным свободных энергий образования

DF°обр Fe2O3 + 3DF°обр Н2О - 2DF°обр Fe(ОН)3 = DF°реакции
-177,1 + 3 ґ (- 56,69) - 2 ґ (-166,0) = -15,17 ккал.

Таким образом, через некоторое время свежеосажденная гидроокись железа превратится в значительно более устойчивый гематит (или гётит).

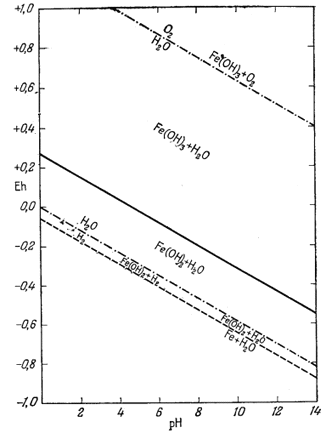Ф и г. 7.4. Диаграмма, показывающая поля устойчивости гидроокиси и гидрозакиси железа при 25° С и 1 атм общего давления. Здесь же проведены границы устойчивости воды. Штриховая линия - метастабильная граница между Fe и Fe(OH)2 в воде.

Точно так же добавление едкой щелочи к раствору соли двухвалентного железа в отсутствие кислорода приведет к образованию гидрозакиси железа - в данном случае вещества отчетливо кристаллического. Но если мы рассмотрим реакцию

3Fe(ОН)2 крист = Fe3O4 крист + Н2 газ + 2Н2Ожидк,

(7.15)

то

DF°обр Fe3O4 + DF°обр H2 газ + 2DF°обр H2O - 3DF°обр Fe(OH)2 = DF°реакции,
-242,4 + 0 + 2 ґ (-56,69) - 3 ґ (-115,57) = - 11,1 ккал,

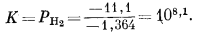Следовательно, Fe(OH)₂ неустойчива и будет разлагаться на магнетит, воду и водород. При общем давлении 1 атм осадок гидрозакиси железа в конце концов разложится с образованием магнетита, причем водород будет пузырьками выделяться из системы до тех пор, пока процесс разложения не закончится.

Тем не менее и гидроокись и гидрозакись железа представляют для нас определенный интерес. Хотя они явно неустойчивы по отношению к гематиту и магнетиту, мы можем изобразить поля их временной устойчивости таким образом, как будто они постоянны. Это необходимо делать в том случае, когда мы хотим исследовать кратковременно существующее равновесие.

Для реакции

Fекрист + 2Н2Oжидк = Fе(ОН)2 крист + 2H+водн + 2e,	(7.16)
Eh = -0,047 - 0,059рН.	(7.17)

Сходным образом

Fе(ОН)2 крист + Н2Oжидк = Fе(ОН)3 крист + Н+водн + е,	(7.18)
Eh = 0,271 - 0,059рН.	(7.19)

Данные уравнения наряду с пределами устойчивости воды графически изображены на фиг. 7.4. Эта диаграмма очень похожа на предыдущую (фиг. 7.3); основное различие между ними заключается в том, что Fe(OH)₂ окисляется до Fe(OH)₃ при более высоком (окислительном) потенциале, чем потенциал, при котором Fe₃O₄ окисляется до Fe₂О₃.

Вышеприведенная диаграмма соотношений между метастабильными соединениями железа лишний раз свидетельствует о том, что все расчеты справедливы только для учитываемых компонентов. Поэтому мы никогда не можем быть полностью уверены в том, что рассматриваемые компоненты действительно устойчивы при данных условиях.

АКТИВНОСТИ ИОНОВ В РАВНОВЕСИИ С ОКИСЛАМИ ЖЕЛЕЗА

После построения диаграммы полей устойчивости для окислов железа можно перейти к рассмотрению основного назначения диаграмм Eh - рН. Поскольку для большого числа ионов значения свободной энергии образования известны, представляется возможным вычислить активности этих ионов в состоянии равновесия с твердыми окислами. Благодаря этому мы облегчаем себе расчеты растворимости различных твердых веществ и можем охарактеризовать условия щелочности - кислотности и окислительного потенциала, в которых данное вещество в разбавленном растворе будет обладать наименьшей растворимостью.

Итак, рассмотрим систему железо - кислород - вода. К растворенным компонентам этой системы, для которых известны данные по их свободной энергии, относятся Fe³⁺_водн, Fе(ОН)²⁺_водн, Fe(OH)⁺_{2 води}, FеО^-_{2 водн}, Fе²⁺_водн, Fе(ОН)⁺_водн и НFеО^-_водн. Первые четыре компонента-ионы трехвалентного железа, а остальные три - двухвалентного. Однако при более или менее полном исследовании соотношений между железом и водой мы не должны были бы ограничиваться только перечисленными компонентами. Например, на растворимость железа может заметно влиять присутствие Fe(OH)⁰₃ води или недиссоциированной растворенной гидрозакиси железа (Винчестер, личное сообщение). И все-таки построение диаграмм, показывающих соотношения одних только изученных компонентов раствора с устойчивыми твердыми веществами, уже представляет собой определенный шаг вперед.

Анализ фиг. 7.3 показывает, что соотношения, определяющие активность растворенных компонентов, выражаются реакциями между устойчивыми в воде твердыми веществами - магнетитом и гематитом, с одной стороны, и растворенными в ней компонентами - с другой. Эти реакции нужно составить таким образом, чтобы выразить их через величины Eh и рН. Большую помощь при расчетах может оказать ряд общих соображений, которые следует учесть прежде, чем написать реакции.

Например, реакции между гематитом и любыми компонентами раствора, содержащими трехвалентное железо, не зависят от Eh, так как здесь не происходит ни окисления, ни восстановления. Напротив, реакции между гематитом и растворенными компонентами, содержащими двухвалентное железо, определенно будут зависеть от величины Eh, но в такой же степени могут определяться величиной рН. Отсюда можно вывести главное правило:
исследование соотношений между растворенными компонентами и твердыми веществами легче начинать с реакций, компоненты которых находятся в одинаковом валентном состоянии.

В общем использованный здесь метод сводится к следующему. Вычисляется активность каждого растворенного компонента, находящегося в равновесии с гематитом и магнетитом; затем на диаграммах Eh - рН в пределах полей устойчивости данных твердых веществ наносятся изолинии этих активностей. После построения частных диаграмм их накладывают друг на друга и получают сводную диаграмму. Последняя дает представление о всех компонентах, для которых известны величины свободных энергий.

Таким образом, если частные диаграммы представляют собой приемлемую неизменяемую черновую запись, то сводные диаграммы можно рассматривать как усовершенствованную запись, поскольку в любой момент она может быть дополнена новыми данными по добавочным компонентам.

И о н   т р е х в а л е н т н о г о   ж е л е з а.   Проведем вначале детальный расчет соотношений между магнетитом, гематитом и активностью иона трехвалентного железа. Учитывая отмеченное выше правило расчетов, прежде всего напишем реакцию между ионом трехвалентного железа и окисью железа и попытаемся выразить ее с учетом воды и водородных ионов:

Fe2О3 крист + 6Н+водн = 2Fе3+водн + 3Н2Oжидк.

(7.20)

Стандартная свободная энергия этой реакции будет равна

2DF°обр Fe3+ + 3DF°обр H2O - DF°обр Fe2O3 - 6DF°обр H+ = DF°реакции,
2 ґ (-2,53) + 3 ґ (-56,69) - (-177,1) - 6 ґ (0) = +2,0 ккал.

Определим константу равновесия

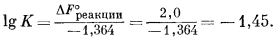Из уравнения константы равновесия исключаем Fе₂О_{3 крист} и Н₂О_жидк, так как их активность равна единице. Тогда

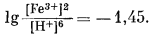Преобразуем полученное выражение, подставив -рН вместо lg [H⁺]:

2lg[Fe3+] = -l,45 - 6pH,
lg[Fe3+] = -0,72 - 3pH.	(7.21)

Как видим, логарифм активности иона трехвалентного железа в равновесии с Fe₂O_{3 крист} представляет собой линейную функцию рН. Если задаться величиной рН, то можно определить [Fe³⁺], и наоборот. Обычно принимают удобные значения [Fe³⁺] и для них находят соответствующие величины рН. Поскольку Eh в этой реакции участия не принимает, изолинии [Fe³⁺] на диаграмме Eh - рН будут параллельны оси Eh.

В табл. 7.1 приведены соответствующие пары значений lg [Fe³⁺] и рН. Величины [Fe³⁺] или активности любых других ионов обычно выбирают в пределах от 10^-1 до 10^-8 или 10^-10. Значения активности, превышающие 10^-1, отвечают уже такой'высокой концентрации, при которой следует ожидать, значительных расхождений между активностью и моляльностью. Кроме того, растворы с активностью данного компонента выше 10^-1 для геолога, как правило, интереса не представляют. Когда же концентрация данного иона меньше 10^-8 (или около одной части Fe³⁺ на 10 млрд.), то активностью или моляльностью этого иона можно пренебречь.

Таблица 7.1

Результаты расчетов по уравнению (7.21); значения рН соответствуют активности Fe³⁺ в равнрвесии с гематитом

lg [Fe3+]	pН	lg [Fe3+]	pН
-1	0,09	-5	1,43
-2	0,43	-6	1,76
-3	0,76	-7	2,09
-4	1,09	-8	2,43

На фиг. 7.5а мы провели изолинии lg [Fe³⁺] по цифровым данным, взятым из приведенной таблицы.

Далее рассмотрим равновесие между ионами трехвалентного железа и магнетитом

Fе3O4 крист + 8Н+водн = ЗFе3+водн + 4H2Oжидк + е.

(7.22)

В данном случае происходит окисление, и поэтому мы вправе составить уравнение реакции полуэлемента, исключив из него вещества с активностью, равной единице:

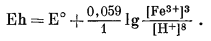Как и прежде, находим DF°_{реакции}, по которой определяем численное значение Е° ; заменив lg[H⁺] на -рН, получаем

Eh = 0,337 + 0,177 lg [Fe3+] + 0,472pH.

(7.23)

Здесь мы сталкиваемся с новым затруднением: теперь недостаточно решать уравнение, задаваясь только значениями [Fe³⁺]; необходимо также выбирать значения для рН или Eh. Однако фактически это дает нам в руки возможность проверить достоверность термодинамических данных. Если мы примем для [Fe³⁺] значение 10^-6 и величину рН, соответствующую равновесию иона с гематитом, то искомая величина Eh для данных [Fe³⁺] и рН должна находиться на границе гематит - магнетит. Действительно, в данной точке оба твердых вещества находятся в равновесии, т. е. все активности ионов, равновесные с одним твердым веществом, будут равновесны и с другим. Если величина Eh в этой точке верна, можно рассчитать наклон изолинии в поле устойчивости магнетита, поскольку при постоянной [Fe³⁺] наклон будет постоянным, и нанести изолинию на диаграмму. Вместе с тем можно произвольно выбирать значения Eh в поле устойчивости магнетита и рассчитывать рН для данной активности иона Fe³⁺.

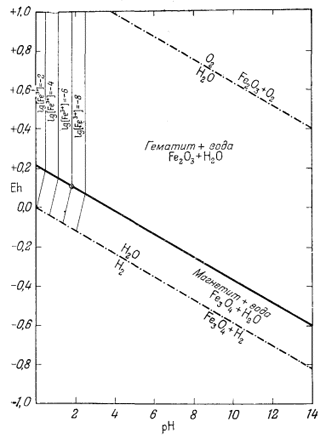Фиг. 7.5а. Активность иона трехвалентного железа в равновесии с гематитом и магнетитом при 25° С и 1 атм общего давления. Проведены изолинии lg[Fe3+]. Обратите внимание, в полях устойчивости обоих твердых веществ активностьFe3+ становиться исчезающе малой в условиях с повышенным значением pH.

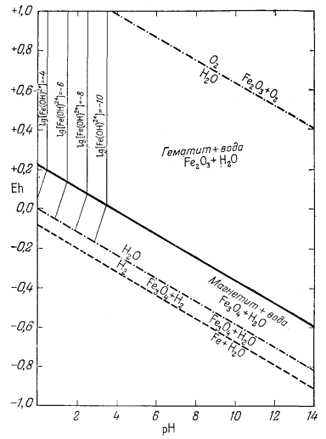Фиг. 7.5б. Активность иона Fe(OH)2+ в равновесии с гематитом и магнетитом при 25° С и 1 атм общего давления в пределах устойчивости воды.

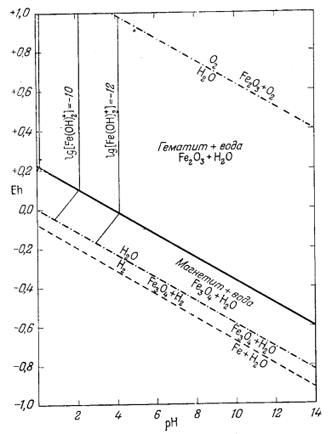Фиг. 7.5в. Активность иона Fe(OH)+2 в равновесии с гематитом и магнетитом при 25° С и 1 атм общего давления в пределах устойчивости воды.

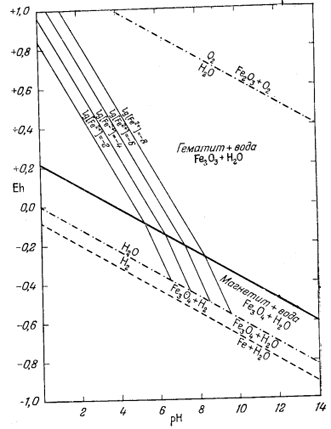Фиг. 7.5г. Активность иона Fe2+ в равновесии с гематитом и магнетитом при 25° С и 1 атм общего давления в пределах устойчивости воды.

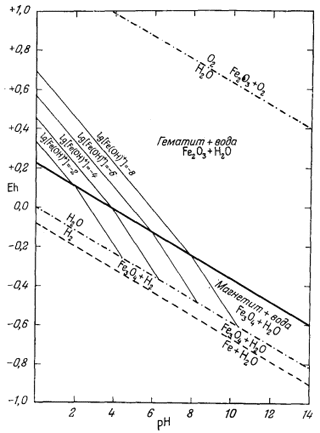Фиг. 7.5д. Активность иона Fe(OH)+ в равновесии с гематитом и магнетитом при 25° С и 1 атм общего давления в пределах устойчивости воды.

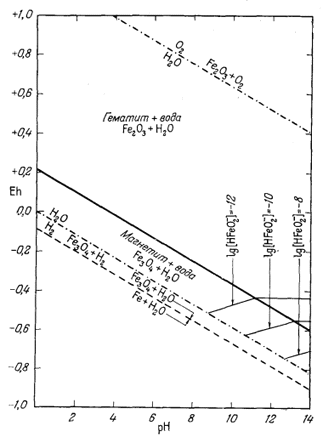Фиг. 7.5е. Активность иона HFeO-2 в равновесии с гематитом и магнетитом при 25° С и 1 атм общего давления в пределах устойчивости воды.

Определим в качестве примера Eh на границе гематит - магнетит для значений lg[Fe³⁺] = -6 и рН = 1,76, взятых из табл. 7.1. Подставив эти цифры в уравнение (7.23), получим

Eh = 0,377 + 0,177 ґ (-6) + (0,472 ґ 1,76) = +0,106.

Рассчитанная точка отмечена на фиг. 7.5а кружочком. Итак, проверка показала, что ошибка находится в пределах точности графика. Изолинии [Fe³⁺] в поле устойчивости магнетита должны проводиться с наклоном 0,472в на единицу рН. Если мы перейдем от активности иона трехвалентного железа к моляльности, то увидим, что m_Fе³⁺ будет совершенно ничтожна при значениях рН, превышающих 2, и довольно низка при рН, равном 1. Между прочим, заметим, что для природных вод роль иона трехвалентного железа часто переоценивается, ибо воды редко обладают рН, равным 2 или меньше.

Проводимые изолинии ограничиваются нижним пределом устойчивости воды, поскольку ниже этого предела Fе³⁺_водн не может находиться в равновесном состоянии. На некоторых последующих диаграммах изолинии активностей будут продолжены в метастабильную область; это мы сделаем для того, чтобы можно было охарактеризовать поведение ионов в тех случаях, когда вода продолжает существовать за пределами своего поля устойчивости.

П р о ч и е  и о н н ы е  к о м п о н е н т ы.  Реакции, выражающие соотношения остальных ионов с гематитом и магнетитом, приводятся в табл. 7.2. Там же даны соответствующие уравнения Eh и рН. Техника расчетов остается такой же, как и для иона трехвалентного железа. Диаграммы, иллюстрирующие положение изолиний активности каждого из этих ионов в полях устойчивости гематита и магнетита, представлены на фиг. 7.5а - 7.5е.

Таблица 7.2

Реакции и уравнения, отражающие соотношения активностей ионов с магнетитом и гематитом

Реакции	Уравнения
А. Fe3+водн
Fe2O3 крист + 6Н+водн = 2Fе3+водн + ЗН2Ожидк Fe3O4 крист + 8Н+водн = 3Fe3+водн + 4Н2Ожидк + е (7.20) (7.22)	lg[Fe3+] = -0,72 - 3pH Eh = 0,337 + 0,177 lg[Fe3+] + 0,472 pH (7.21) (7.23)
В. Fe(OH)2+водн
2Fе(ОН)2+водн + Н2Oжидк = Fе2О3 крист + 4H+водн Fе3O4 крист + 5H+водн = ЗFе(ОН)2+водн + H2Oжидк + e (7.24) (7.26)	lg[FeOH2+] = -3,151 - 2рН Eh = 0,780 + 0,177 lg[FeOH2+] + 0,295 рН (7.25) (7.27)
С. Fe(OH)+2 воодн
Fe2O3 крист + H2Ожидк + 2Н+водн = 2Fe(OH)2+2 водн Fе3O4 крист + 2Н2Ожидк + 2Н+водн = 3Fе(ОН)+2 водн + е (7.28) (7.30)	lg[Fe(OH)+2] = -7,84 - pH Eh = 1,61 + 0,177 lg[Fe(OH)+2] + 0,118 рН (7.29) (7.31)
D. Fe2+2 водн
2Fе2+водн + 3Н2Oжидк = Fe2O3 жидк + 6Н+водн + 2e 3Fе2+водн + 4H2Oжидк = Fe3O4 крист = 8H+водн + 2e (7.32) (7.34)	Eh = 0,728 - 0,059 lg[Fe2+] - 0,177 рН Eh = 0,980 - 0,0885 lg[Fe2+] - 0,236 рН (7.33) (7.35)
E. Fe(OH)+водн
2Fе(ОН)+водн + H2Oжидк = Fe2O3 крист + 4H+водн + 2e 3Fe(OH)+водн + H2Oжидк = Fе3О4 крист + 5Н+водн + 2е (7.36) (7.38)	Eh = 0,217 - 0,059 lg[Fe(OH)+] - 0,118 рН Eh = 0,214 - 0,0885 lg[Fe(OH)+] - 0,148 рН (7.37) (7.39)
F. HfeO-2 водн
2НFеО-2 вoдн = Fe2O3 крист + Н2Oжидк + 2е 3HFeO-2 вoдн + H+вoдн = Fe3O4 крист + 2Н2Oжидк + 2e (7.40) (7.42)	Eh = - 1,139 - 0,059 lg[HFeO-2] Eh = -1,819 - 0,0885 lg[HFO-2] + 0,0295 рН (7.41) (7.43)

СВОДНАЯ ДИАГРАММА

На фиг. 7.6 приведена сводная диаграмма, которая составлена в соответствии с правилами, предложенными Пурбэ. Граница поля устойчивости данного твердого вещества условно проведена через точки, в которых сумма активностей ионов, находящихся в равновесии с данным твердым веществом, превышает некоторую принятую величину. Для геологических целей принята величина 10^-6, основанная на следующей предпосылке. Если сумма активностей известных компонентов раствора, находящихся в равновесии с каким-либо твердым веществом, меньше 10^-6, то это твердое вещество будет вести себя в данной среде как неподвижный компонент. Это правило, выведенное в основном из опытов, по-видимому, хорошо увязывается с данными минералогии. На диаграмме изображена также изолиния суммы активностей ионов, равной 10^-4. Эта изолиния характеризует изменение "растворимости" в зависимости от рН и Eh. Между полями ионов проведены границы, а каждое поле обозначено индексом преобладающего иона. Граница поля какого-либо иона показана там, где активность данного иона становится равной активности иона, преобладающего в смежном поле. Если мы рассмотрим фиг. 7.5а - 7.5е, то увидим, что в полях, обозначенных на фиг. 7.6 индексами Fе²⁺_водн и Fе³⁺_водн, действительно резко преобладают ионы двухвалентного, и трехвалентного железа, а активность других ионов, за исключением отдельных небольших участков, ничтожна.

Поскольку активность ионов, находящихся в равновесии с твердыми веществами, довольно быстро меняется с изменением Eh и рН, то лишь в редких случаях какой-либо участок диаграммы Eh - рН нельзя с уверенностью охарактеризовать через единственный ион, активность которого составляла бы 99% или более суммарной активности всех ионов.

Существует несколько методов построения сводных диаграмм. Один из них мы рекомендуем геологам, имея в виду их опыт в обращении с топографическими картами. Этот метод заключается в следующем. Сначала изготавливают кальки с частными диаграммами Eh - рН для отдельных ионов, а потом такие кальки накладывают друг на друга. Границы полей легко

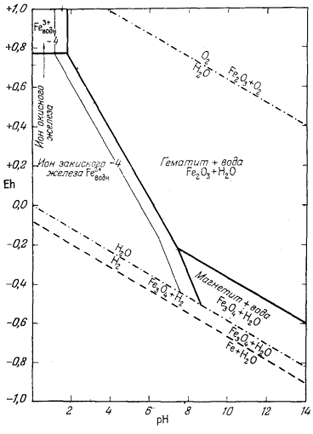Фиг. 7.6. Сводная диаграмма полей устойчивости гематита и магнетита в воде при 25° С и 1 атм общего давления. К полям ионов отнесены такие участки, в которых суммарная активность растворенных компонентов превышает 10-6. Поля ионов обозначены индексами соответствующих компонентов. Изолиния lg[растворенные компоненты] = - 4 проведена для того, чтобы показать характер изменения активности.

определяются путем соединения точек пересечения равных изолиний, что и продемонстрировано на примере ионов Fе²⁺_водн и Fе³⁺_водн на фиг. 7.6.

Сводную диаграмму можно рассчитать и аналитически, если написать реакции между ионами и затем определить Eh и рН условий, при которых активности этих ионов равны. Например, если мы напишем

Fе2+водн = Fе3+водн + е,

(7.44)

то

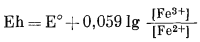(7.45)

А при условии, что Fе²⁺_водн = Fе³⁺_водн, Eh = E°. Следовательно, граница между ионами определяется значением E° для реакции полуэлемента, равным 0,771 в.

Сходным образом определяем границу между ионами Fе²⁺_водн и Fе(ОН)⁺_водн:

Fе2водн + Н2Ожидк = Fе(ОН)+водн + H+водн	(7.46)
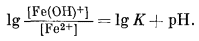	(7.47)

Когда активности рассматриваемых ионов равны, то рН = -lg К. В данном случае равенство активностей ионов Fе²⁺_водн и Fе(ОН)⁺_водн достигается при столь высоких значениях рН, когда ни для одного из этих ионов активность не может быть больше 10^-6. Другими словами, Fe(OH)⁺ не становится преобладающим ионом в пределах поля, которое мы условно обозначили как поле его "растворимости".

Весьма отрадно отметить, что как в разобранном примере с гидроокислами железа, так и во многих последующих диаграммах все нужные нам главные ионы разбавленных растворов - наши старые друзья. Другими словами, в рядовых лабораториях открывают и описывают прежде всего такие ионы, к которым мы привыкли и которые поэтому стремимся обнаружить. И только при все большем и большем усовершенствовании наших методов или в результате их распространения на новые, необычные условия можно обнаружить поля, где привычные нам компоненты уступают место другим, незнакомым.

К одной из любопытных особенностей сводной диаграммы железа относится резкая ограниченность поля иона трехвалентного железа. Только в очень кислых и сильно окислительных условиях активность этого иона превышает 10^-6. Высокая устойчивость гематита с очевидностью доказывается размерами его поля, которое охватывает диапазон от умеренно кислой окислительной среды до сильно восстановительных нейтральных и щелочных условий. В данной системе "растворимость" почти целиком обусловливается концентрацией иона двухвалентного железа, поле которого в восстановительной обстановке глубоко проникает в поля устойчивости твердых веществ. Ни у гематита, ни у магнетита в пределах рН от 0 до 14 не обнаружено заметных амфотерных свойств. Активность иона HFeO^-₂ нигде не превышает 10^-6, так что ему даже не нашлось места на сводной диаграмме.

ВЛИЯДИЕ CO₂ НА СООТНОШЕНИЯ В СИСТЕМЕ ЖЕЛЕЗО
- ВОДА - КИСЛОРОД

В природных средах железо находится как в виде магнетита и гематита, так и в виде карбоната железа - сидерита, а также в форме сульфидов или силикатов железа. Таким образом, следующим нашим шагом должно быть изучение влияния CO₂ на соотношения устойчивости магнетита и гематита. Исходя из ранее составленных диаграмм парциальных давлений, нетрудно вывести зависимость между Eh, рН и Р_CO2 Так как Р_O2 можно рассматривать как функцию двух переменных - Eh и рН, то взаимоотношения сидерита с гематитом и магнетитом можно представить на трехмерной диаграмме, осями координат которой будут служить Eh, рН и Р_CO2.

УСТОЙЧИВОСТЬ КАК ФУНКЦИЯ P_CO2

Чтобы вывести эту зависимость, необходимо написать реакции между магнетитом и сидеритом и между гематитом и сидеритом. Начнем с изучения соотношений сидерита с гематитом

2FеСО3 крист + Н2Oжидк = Fе2O3 крист +2СO2 газ +2H+водн + 2е.

(7.48)

Этой реакции соответствует следующее уравнение Eh:

Eh = E° + 0,059 lg PCO2 - 0,059pH,	(7.49)
Eh = 0,286 + 0,059 lgPCO2 - 0,059pH.

Проделаем то же для реакции между сидеритом и магнетитом:

3FеСО3 крист + Н2Ожидк = F3O4 жидк + 3СО2 газ + 2H+водн + 2е	(7.50)
Eh = 0,319 + 0,0885 lgPCO2 - 0,059pH.	(7.51)

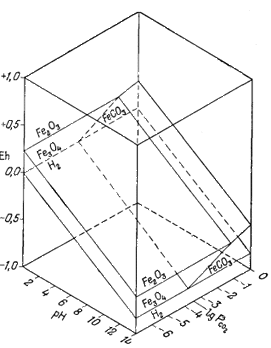Фиг. 7.7. Устойчивость гематита, магнетита и сидерита как функция Eh, pH и PCO2, при 25° С и 1 атм общего давления. Указанные соотношения ограничены нижним пределом устойчивости воды. Двойной стрелкой у оси lgPCO2 отмечена величина парциального давления СО2 в современной земной атмосфере.

Диаграмма, отражающая указанные соотношения, приведена на фиг. 7.7. Передней плоскостью объемной диаграммы служит двумерная диаграмма соотношений гематит - магнетит в координатах Eh - рН, В качестве третьего измерения использовано P_CO2, a поскольку устойчивость гематита и магнетита не зависит от Р_CO2, то границы их полей будут представлять собой плоскости, параллельные оси Р_CO2. Вместе с тем в уравнения (7.49) и (7.51) входят все три переменные величины, а поэтому соответствующие им плоскости будут наклонены ко всем трем осям координат; по наклону этих плоскостей можно видеть, как с увеличением Р_CO2 поля магнетита и гематита замещаются полем сидерита. Двойной стрелкой на диаграмме отмечено значение парциального давления СО₂ в земной: атмосфере, равное 10^-3,5 атм. Интересно, что в этих условиях сидерит характеризуется очень небольшим полем устойчивости. Магнетит полностью замещается сидеритом, если Р_CO2 достигает величины примерно 10^-1,4 атм.

Трехмерная диаграмма пригодна для изображения только самых общих соотношений в системах, но во многих случаях удобнее использовать серию сечений частных диаграмм при постоянных P_CO2. Особенно удобно применять такие сечения в случае, когда нам нужно отразить равновесные активности растворенных ионов.

На фиг. 7.8а представлено сечение трехмерной диаграммы (фиг. 7.7) при Р_CO2 = 10^-2,0 атм. Граница между сидеритом и магнетитом наносится непосредственно по уравнению (7.51), что значительно легче, чем переносить данные с фиг. 7.7. На фиг. 7.86 показана активность растворенных ионных компонентов, теперь уже при наличии в нашей системе сидерита. Поскольку поле устойчивости сидерита по отношению к гематиту и магнетиту определяется из уравнений (7.49) и (7.51), диаграмму активностей гематит - магнетит - ионы, построенную ранее (фиг. 7.6), необходимо изменить только в пределах поля устойчивости новой твердой фазы - сидерита. На первый

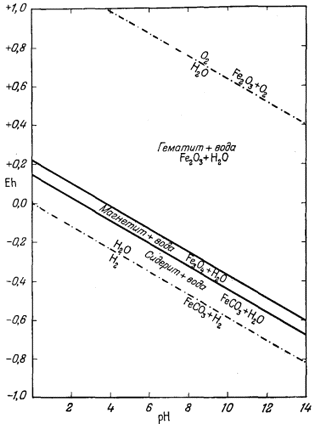Фиг. 7.8а. Устойчивость Fe2O3, Fe3O4 и FeCO3 при 25° С и 1 аmм общего давления и PCO2, равном 10-2,0 атм. Соотношения указаны только в пределах устойчивости воды.

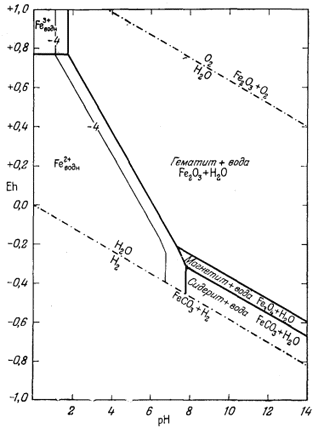Фиг. 7.8б. Устойчивость Fe2O3, Fe3O4 и FeCO3 при 25° С и 1 аmм общего давления и PCO2, равном 10-2,0 атм. Проведена изолиния суммарной активности ионов, равной 10-4. Поля твердых фаз ограничены линией суммарной активности ионов, равной 10-4. Соотношения указаны только в пределах устойчивости воды.

взгляд может показаться, что при этом необходимо рассчитать равновесия между сидеритом и ионами Fe³⁺, Fe(OH)²⁺, Fe(OH)⁺₂, HFeO^-₂, Fe(OH)⁺ и Fe²⁺. Однако поскольку единственным определяющим ионом в поле устойчивости магнетита, теперь занятого сидеритом, является ион Fe²⁺ (>10^-6), а сидерит еще более устойчив, чем магнетит, то естественно, что и активности всех ионов в равновесии с сидеритом будут меньше, чем они были для магнетита. Поэтому, как и прежде, нам необходимо рассмотреть активность одного только иона Fe²⁺. Для этого достаточно написать одну реакцию

FеСО3 крист + 2Н+водн = Fе2+водн + СО2 газ + Н2Ожидк.

(7.52)

Этой реакции соответствует уравнение

lg[Fe2+] = 7,47 - lgPCO2 = 2pH.

(7.53)

По условию Р_СО2 постоянно и равно 10^-2,0; поэтому lg[Fe²⁺] зависит только от рН, а изолинии Fe²⁺ на диаграмме будут параллельны оси Eh, В случае если использованные значения свободных энергий, а также расчеты и графические построения, проведенные нами, верны, изолинии Fe²⁺ в поле FeCO₃ должны сойтись с соответствующими изолиниями, перенесенными из диаграммы полей устойчивости магнетит - гематит.

В условиях земной атмосферы, т.е. при Р_CO2 = 10^-3,5 атм, поле устойчивости FеСО₃ так мало, что почти не поднимается над нижним пределом устойчивости воды. Поэтому мы и были вынуждены, показывая поведение иона Fe²⁺ в растворе, выбрать сечение при несколько большем Р_CO2.

УСТОЙЧИВОСТЬ КАК ФУНКЦИЯ еСО₂

Вышеизложенный ход рассуждений привел нас к выводу, что сидерит неравновесен в присутствии атмосферы. Между тем известно, что он относится к одному из ведущих первичных минералов осадочных железных руд. Отсюда следует, что образование природного сидерита могло происходить лишь в резко восстановительных условиях в присутствии такого количества СО₂, которое намного превышало его содержание в атмосфере. Попытаемся теперь рассмотреть зависимость устойчивости сидерита от суммы растворенных карбонатов. При какой концентрации карбонатного или бикарбонатного иона в растворе, свободном или почти свободном от кислорода, сидерит становится устойчивым по отношению к магнетиту? Можно ли найти эти необходимые концентрации среди известных нам анализов обычных подземных вод? Рассматривая природную воду, где сумма моляльностей растворенных карбонатных ионов (H₂CO₃ + HCO^-₃ + СO^2-₃) равна 10^-2 (примерно 600 ч. на млн.), попытаемся выяснить, будет ли сидерит устойчив, а если будет, то в каких условиях.

Поставленная задача в основном аналогична третьему случаю, разобранному нами в гл. 3. Итак, сумма карбонатов в растворе известна. Каковы будут соотношения в системе при произвольно выбранных значениях Eh - рН?

Один из методов решения заключается в следующем. Определяется положение изолиний [СО^2-₃] в зависимости от рН, а затем на основании соотношения

[Fе2+][СО2-3] = KFeCO3

(7.54)

определяем положение изолинии [Fe²⁺].

Далее, накладывая рассчитанные таким образом изолинии [Fe²⁺] на диаграмму равновесия [Fe²⁺] с Fe₂O₃ и Fе₃O₄ (фиг. 7.5г), находим поле устойчивости FeCO3. Оно представляет собой тот участок диаграммы, для которого [Fe²⁺] оказывается меньшей в равновесии с FеСО₃, чем в равновесии с магнетитом и гематитом.

Проиллюстрируем оба метода. Первый из них, вероятно, полезнее, так как его можно использовать независимо от сложности рассматриваемой системы. Если активность данного иона в равновесии с данным твердым веществом меньше активности того же иона в равновесии с любым другим твердым веществом, то на диаграмме область этого минимума и представит собой поле устойчивости первого твердого вещества.

Поскольку сумма карбонатов в растворе равна 10^-2, мы можем, не совершая серьезной ошибки (гл. 3), написать

[H2CO3] + [HCO-3] + [СО2-3] = 10-2,	(7.55)
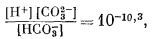	(7.56)
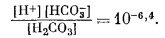	(7.57)

Так как мы знаем, что в природных условиях карбонатные компоненты не восстанавливаются и не окисляются (за исключением, может быть, некоторых особых случаев^{1 (стр.176)}.), то Eh можно не учитывать, и тогда изолинии СО^2-₃ будут параллельны оси Eh. Уравнения (7.55) - (7.57) можно решить в отношении значений [Н⁺] и [СO^2-₃]; для этого сначала выразим [HCO^-₃] через [Н⁺] и [СO^2-₃] по уравнению (7.56), а затем используем полученное значение и выразим [Н₂СО₃] через [Н⁺] и [СO^2-₃] по уравнению (7.57). В заключение подставим эти величины в уравнение (7.55):

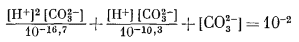и после упрощения получим

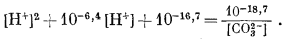(7.58)

Подставляя в это уравнение любое значение [СO^2-₃], мы можем рассчитать соответствующую величину рН. Результаты подобных расчетов представлены на фиг. 7.9.

Теперь подставим численное значение К в уравнение (7.54) и прологарифмируем его:

lg[Fe2+] = -10,67 - lg[CO2-3].

(7.59)

Итак, для каждой изолинии lg[CO^2-₃] можно найти положение соответствующей изолинии lg[Fe²⁺]. На фиг. 7.10 совмещены изолинии [Fe²⁺], равновесные по отношению к FеСО₃ и по отношению к Fe₂O₃ и Fе₃O₄ (взято из данных фиг. 7.5г); здесь же проведена граница между полями устойчивости FеСО₃ и окислов железа. Фиг. 7.11 представляет собой сводную диагпрлшу устойчивости окислов железа и сидерита, полученную путем совмещения фиг. 7.10 и 7.6. Сопоставьте фиг. 7.8б, построенную для постоянного Р_CO2, с фиг. 7.11, построенной для постоянной суммы растворенного карбоната. В последнем случае при рН, равном примерно 10,5, [СO^2-₃] достигает своего максимума и далее остается постоянной. В то же время при постоянном Р_CO2 с повышением рН активность иона СO^2-₃ непрерывно возрастает. На диаграмме, построенной для постоянной суммы растворенных карбонатов, эта зависимость выражается в сокращении поля устойчивости сидерита

1 (стр.176) В действительности некоторые карбонатные компоненты вблизи нижнего предела устойчивости воды неустойчивы по отношению к углероду. Этот факт может иметь значительный геологический смысл, но в настоящей работе мы его не будем принимать во внимание.

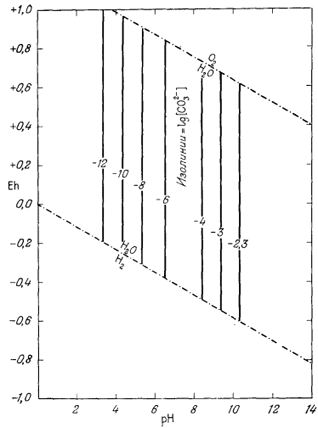Фиг. 7.9. Изолинии lg[CO2-3] на диаграмме справедливы при условии, что [H2CO3] + [HCO-3] + [CO2-3] = 10-2 при температуре 25° С и 1 аmм общего давления.

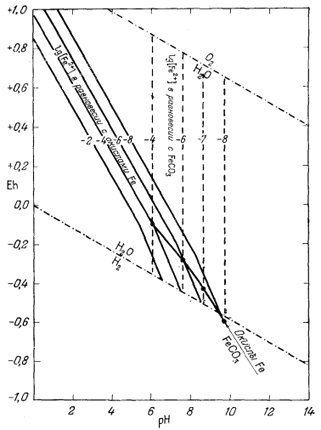Фиг. 7.10. Поле устойчивости FeCO3 по отношению к окислам железа (устанавливается путем выявления участка, в котором [Fe2+], равновесная с FeCO3, меньше, чем [Fe2+], равновесная с окислами железа). В растворе сумма моляльностей H2CO3 + HCO-3 + CO2-3 равна 10-2 моль при 25° С и 1 аmм общего давления. Штриховые линии - положение изолиний lg[Fe2+] в равновесии с FeCO3; сплошные линии - то же в равновесии с окислами железа. Жирные точки - равные значения [Fe2+].

при высоких значениях рН и в увеличении устойчивости окислов железа с увеличением рН (поскольку они осаждаются ионами ОН^-). Устойчивость же сидерита при значениях рН, превышающих 10,5, не изменяется. Другими словами, в системе, закрытой для СО₂, выпадение в осадок сидерита или магнетита зависит только от изменения величины рН и не зависит от окислительно-восстановительных условий. Однако в открытой системе при постоянном Р_CO2 замена сидерита магнетитом (в осадке) не может происходить без изменения Р_O2.

Чтобы найти поле устойчивости сидерита вторым методом, нужно прежде всего определить, в каком участке диаграммы рН - Eh данный карбонатный компонент раствора количественно преобладает над всеми другими компонентами. Из уравнений

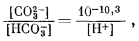	(7.56)
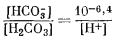	(7.57)

можно видеть, что активность карбонатного дона равна активности бикарбоната при рН 10,3, а активность бикарбоната равна активности угольной кислоты при рН 6,4. Следовательно, при значениях рН ниже 6,4 основным компонентом раствора будет Н₂СО₃; при значениях рН от 6,4 до 10,3 на смену придет ион HCO^-₃, а при рН свыше 10,3 будет преобладать ион СO^2-₃. Поскольку указанные границы определяются отношением активностей, они справедливы для любой суммы растворенных карбонатов. В применении к разбавленным растворам (при ионной силе Ј 0,2) можно также без особой ошибки считать, что все количество растворенного СО₂ обусловливается концентрацией преобладающего компонента в средней части его поля.

Таким образом, если суммарная концентрация CO₂ равна 10^-2 М, а величина рН не превышает 6,4, мы можем написать, что

3FеСО3 крист + 4Н2Oжидк = Fе3O4 жидк +3Н2СО3 водн + 2H+водн + 2е

(7.60)

а результат выразить только через Eh и рН, ибо активность H₂CO_{3 водн} равна 10^-2. Для поля, где преобладающим компонентом служит ион НСО^-₃, соответствующая реакция будет, выглядеть следующим образом:

3FеСО3 крист + 4Н2Oжидк = Fе3O4 крист + 3НСО-3 водн + 5H+водн + 2e,

(7.61)

а в поле иона СО^2-₃

3FеСО3 крист + 4Н2Oжидк = Fe3O4 крист + 3СО2-3 водн + 8Н+водн + 2е

(7.62)

Выразим эти реакции через Eh и рН:

Eh = 0,445 - 0,059рН + 0,0885 lg[H2CO3],	(7.63)
Eh = l,010 - 0,148pH + 0,0885 lg[HCO-3],	(7.64)
Eh = 1,920 - 0,236рН + 0,0885 lg[СО2-3].	(7.65)

Кроме того, мы должны рассмотреть соотношения между FеСО₃ и Fе₂О₃:

2FеСО3 крист + 3Н2Ожидк = Fе2О3 крист + 2Н2СО3 водн + 2Н+водн + 2е,	(7.66)
2FеСО3 крист + 3Н2Ожидк = Fe2О3 крист + 2НСО-3 водн + 4Н+водн + 2e,	(7.67)
2FеСО3 крист + 3Н2Ожидк = Fе2О3 крист + 2СО2-3 водн + 6Н+водн + 2е.	(7.68)

Этим реакциям соответствуют следующие уравнения:

Eh = 0,370 - 0,059рН + 0,059 lg [Н2СО3],	(7.69)
Eh = 0,747 - 0,118рН + 0,059 lg [HCO-3],	(7.70)
Eh = 1,359 - 0,177рН + 0,059 lg[CO2-3].	(7.71)

Все шесть уравнений (7.63) - (7.65) и (7.69) - (7.71) графически изображены на фиг. 7.12; там же проведены границы между полями карбонатных компонентов, рассчитанные по уравнениям (7.56) и (7.57). Заметим, что на графиках все реакции не выходят за пределы поля преобладания рассматриваемого иона; например, реакция перехода FeCO₃ в Fe₂O₃ указана только в пределах значений рН от 0 до 6,4, т. е. в поле, где практически вся сумма растворенных карбонатов определяется концентрацией Н₂СО₃. Стабильность и метастабильность реакций определяются в направлении окисления от нижней части диаграммы к верхней. В поле H₂CO₃ магнетит не может переходить в Fe₂O₃, так как FeCO₃ еще не окислилось до Fe₃O₄, a FeCO₃ переходит в Fe₂O₃ еще раньше, чем оно окисляется до Fe₃O₄. Следовательно, в этой части диаграммы стабильной реакцией будет непосредственный переход от FeCO₃ до Fe₂O₃.

Как показывает анализ фиг. 7.12, при рН 6,4 и 10,3 резко изменяется наклон линий реакций. В действительности эти линии должны иметь плавный перегиб, так как концентрация преобладающего компонента около граничных значений рН не равна 10^-2. Все стабильные границы перенесены с фиг. 7.12 на фиг. 7.13, которая, таким образом, иллюстрирует соотношения между FeCO₃, Fe₂O₃ и Fe₃O₄ при суммарной концентрации карбоната в растворе, равной 10^-2.

Поскольку таким методом мы определили положение полей устойчивости твердых веществ, можно найти и положение изолинии для [Fe²⁺] = 10^-6, воспользовавшись при этом следующим соотношением:

FеСО3 крист + H+водн = Fе2+водн + НСО-3 водн.

(7.72)

В поле преобладания иона HCO^-₃ (при значениях рН от 6,4 до 10,3) активность его считается равной 10^-2, а поэтому равновесные соотношения определятся равенством

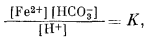или

lg[Fe2+] - 2 + pH = lgK.

(7.73)

Если рассчитать К по данным свободной энергии, то уравнение примет вид

lg[Fe2+] = - 0,33 - pH + 2.

(7.74)

Подставив -6 вместо lg[Fe²⁺], рассчитаем рН, который окажется равным 7,67; эта величина хорошо согласуется с результатом, полученным ранее графическим путем (фиг. 7.11). Изолиния lg[Fe²⁺] = -6 показана на фиг. 7.13 штриховой линией. Поле FeCO₃, ограниченное этой линией, границей между FеСО₃ и Fe₃O₄, а также нижним пределом устойчивости воды, идентично полю, определенному по ранее разобранному методу (фиг. 7.10).

Если увеличить сумму растворенного карбоната, то поле устойчивости сидерита расширится; если эту сумму уменьшить, то поле сократится. Если за поле устойчивости сидерита считать участок диаграммы, в котором активность растворенных железосодержащих компонентов не превышает 10^-6, то при суммарной концентрации растворенного карбоната, меньшей 10^-3, поле сидерита вообще исчезнет.

Вместе с тем при ранее принятой сумме растворенных карбонатов (10^-2) поле устойчивости сидерита окажется значительно большим но отношению к свежеосажденным гидроокислам железа, что и показано на фиг. 7.14. Эту диаграмму можно рассматривать как "экспериментальную", так как изученные экспериментальным путем условия осаждения железа довольно хорошо

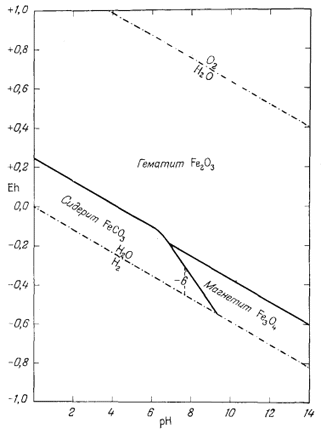Фиг. 7.13. Поля устойчивости гематита, магнетита и сидерита в воде при 25° С и 1 атм общего давления и суммарной концентрации растворенного карбоната, равной 10-2. Штриховая линия проведена для lg [Fe2+] = -6.

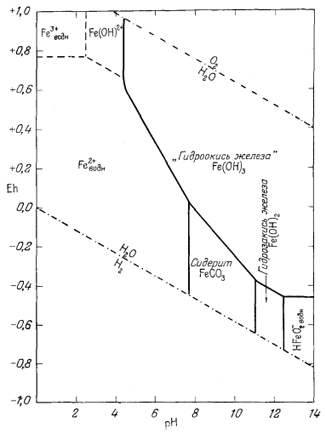Фиг. 7.14. Диаграмма, иллюстрирующая соотношения между неустойчивыми гидроокислами железа и сидеритом при 25° С и 1 атм общего давления. За границу между полями твердых веществ и ионов принята суммарная активность растворенных компонентов, равная 10-4. Сумма растворенных карбонатных компонентов равна 10-2. Штриховые линии - границы между полями преобладания отдельных ионов.

укладываются в рамки указанных в ней соотношений. Заметим, что из-за меньшей устойчивости гидроокислов железа на диаграмме появляются поля Fe(OH)²⁺ и HFeO^-₂.

ВЛИЯНИЕ СЕРЫ НА СООТНОШЕНИЯ В СИСТЕМЕ ЖЕЛЕЗО -
ВОДА - КИСЛОРОД

Добавление CO₂ к системе железо - вода - кислород позволило оценить устойчивость сидерита по отношению к окислам железа; добавление к той же системе серы по аналогии должно дать нам сведения о соотношениях

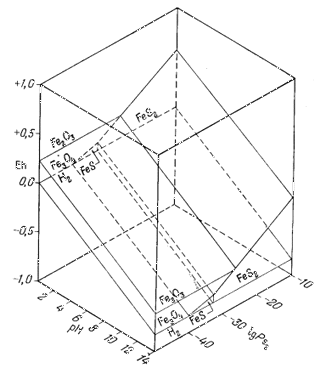Фиг. 7.15. Соотношения устойчивости Fе2О3, Fe3O4, FeS и FeS2 как функция Eh, pH и lgPS2 при 25° С и 1 аmм общего давления в присутствии воды. Обратите внимание на небольшие размеры поля устойчивости FeS и на малые величины PS2 , при которых возможна ассоциация пирита, пирротина и магнетита.

окислов железа с пиритом и пирротином. Для этой цели, как и в случае системы с CO₂, лучше всего построить диаграмму с тремя переменными - Eh, pH и P_S2. Как и ранее, мы можем начать с рассмотрения взаимоотношений магнетита и гематита в воде и написать реакции перехода этих веществ в пирротин и пирит при добавлении к системе серы:

3FеSкрист + 4Н2Ожидк = Fe3O4 крист + 3/2S2 газ + 8Н+водн + 8е,	(7.75)
2FеSкрист + 3Н2Ожидк = Fe2O3 крист + S2 газ + 6H+водн + 6е,	(7.76)
3FеS2 крист + 4Н2Ожидк = Fе3O4 крист + 3S2 газ + 8Н+водн + 8е,	(7.77)
2FeS2 крист + 3Н2Ожидк = Fe2O3 крист + 2S2 газ + 6H+водн + 6е.	(7.78)

Этим реакциям соответствуют уравнения для Eh и рН:

Eh = 0,444 + 0,011 lgPS2 - 0,059pH,	(7.79)
Eh = 0,419 + 0,0098 lgPS2, - 0,059pH,	(7.80)
Eh = 0,811 + 0,0221 lgPS2 - 0,059pH,	(7.81)
Eh = 0,746 + 0,0197 lgPS2 - 0,059pH.	(7.82)

Кроме того, мы должны рассмотреть соотношение между пирротином и пиритом

2FеSкрист + S2 газ = 2FeS2 крист.

(7.83)

Последнее равенство характеризуется определенным P_S2 и независит от Eh и рН. Для этого случая P_S2 равно 10^-33 атм.

Проще всего начать построение диаграммы с сечения Eh - lgP_S2 при рН = 0, нанеся на него все равновесные соотношения. Затем, исключив метастабильные реакции, можно вычертить соответствующие плоскости и получить таким образом трехмерную диаграмму. После исключения метастабильных границ подобное построение не представляет особых затруднений, так как все линии будут иметь один и тот же наклон, кроме той, которая соответствует реакции (7.83). Построенная нами диаграмма приведена на фиг. 7.15. Поражает сходство ее с диаграммой для системы Eh - рН - Р_CO2 (фиг. 7.7).

УСТОЙЧИВОСТЬ КАК ФУНКЦИЯ SS

Как мы убедились на примере диаграмм с участием CO₂, в ряде случаев полезно строить сечения трехмерных диаграмм, параллельные осям Eh и рН при постоянном P_S2. Техника построения таких сечений рассмотрена выше для систем с СО₂, и здесь мы на ней останавливаться не будем. Вместе с тем при изучении систем с постоянным количеством растворенной серы возникают новые осложнения. Если в первом случае в растворе находились только три основных компонента - Н₂СО₃, НСО^-₃ и CO^2-₃ -, устойчивость которых не зависела от Eh, то для серы выделено и изучено уже около 40 ионных и молекулярных компонентов, причем на их устойчивость существенно влияет как Eh, так и рН среды. К счастью, Валенси [7] показал, что в природных условиях обычно встречаются лишь такие компоненты, которые оказываются устойчивыми при комнатной температуре и при наличии достаточно высоких концентраций. Валенси построил диаграммы для таких главных компонентов, к которым отнес только сульфат-ион, бисульфат-ион, самородную серу, сероводород, бисульфид-ион и сульфид-ион. Как и в случае с карбонатами, мы можем составить реакции с участием растворенных компонентов, ограничив их полем, в котором суммарная активность растворенной серы определяется главным образом активностью самой серы.

Диаграмму с полями преобладания серусодержащих компонентов построить нетрудно. Вместо того чтобы делать "формальное" построение с учетом всех возможных равновесии и затем исключать из него метастабильные реакции, мы предлагаем более рациональную методику, которая практически сильно сокращает процедуру построения диаграмм устойчивости для большинства систем.

Построенная диаграмма в ее окончательном виде приведена на фиг. 7.16. Нижеследующие данные необходимо дополнить чтением рекомендуемой литературы. Итак, прежде всего мы можем быть уверены, что в кислой восстановительной среде устойчивым серусодержащим компонентом будет H₂S, который при повышении рН сменится ионами HS^- и S^2-, согласно уравнениям

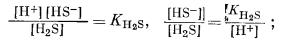	(7.84)
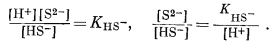	(7.85)

Следовательно, [H₂S] = [HS^-] при K_H2S = [Н⁺], a [HS^-] = [S^2-] при К_HS^- = [Н⁺]. Константы К_H2S и К_HS^- равны соответственно 10^-7

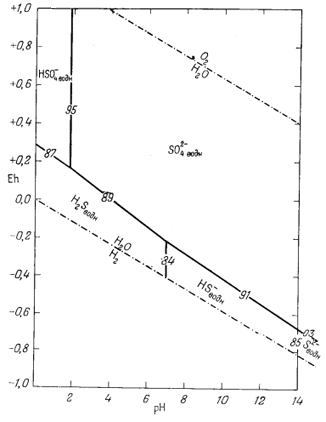Фиг. 7.16. Положение полей преобладания серусодержащих компонентов в воде при 25° С и 1 атм общего давления. Цифры на линиях соответствуют номерам уравнений в тексте.

и 10^-14, а поэтому границы между полями данных трех компонентов будут представлены вертикальными линиями при значениях рН 7 и 14.

Окисление H₂S при постоянном значении рН приведет к образованию ионов HSO^-₄ или SO^2-₄, a HS^- и S^2- будут окисляться до SO^2-₄. Приведем эти реакции и соответствующие им уравнения Eh:

H2Sводн + 4H2Oжидк = HSO-4 водн + 9H+водн + 8e,	(7.86)
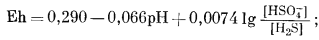	(7.87)
H2Sводн + 4H2Oжидк = SO2-4 водн + 10H+водн +8e,	(7.88)
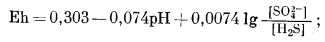	(7.89)
HS-водн + 4H2Oжидк = SO2-4 водн + 9H+водн + 8e,	(7.90)
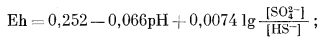	(7.91)
S2-водн + 4H2Oжидк = SO2-4 водн + 8H+водн +8e,	(7.92)
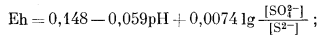	(7.93)

При равенстве активностей двух серусодержащих компонентов, например при [S^2-] = [SO^2-₄], последний член в уравнениях Eh становится равным нулю, а поэтому границы между полями соответствующих ионов определяются только как функции Eh и рН.

Наконец, границу между полями HSO^-₄ и SO^2-₄ определяем на основании реакции

HSO-4 водн = Н+водн + SO2-4 водн,	(7.94)
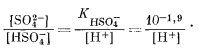	(7.95)

Соотношения, получившие свое отражение на фиг. 7.16, зависят от валового содержания серы в растворе; они характеризуют только те условия, в которых отношения серусодержащих компонентов равны единице.

Рассматривая систему с определенной величиной суммарной активности растворенной серы, равной, например, 10^-1, мы исходим из предположения, что активность какого-либо иона в пределах его поля будет очень близка к 10^-1. Этот момент можно использовать при расчетах содержания прочих серусодержащих ионов в пределах того же поля. Например, в пределах поля активность сульфид-иона определяется следующим образом:

H2Sводн = S2-водн + 2Н+водн,	(7.96)
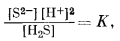lg [S2-] = -22 + 2pH.	(7.97)

Раз уж мы задались суммой растворенной серы SS, то интересно проверить, может ли это количество растворенной серы оставаться в растворе в равновесии с самородной серой как с возможной твердой фазой. Чтобы решить этот вопрос, напишем реакции для различных компонентов при условии равновесия их с серой:

Н2Sводн = Sкрист + 2Н+водн + 2е,	(7.98)
НS-водн = Sкрист + Н+водн + 2е,	(7.99)
S2-водн = Sкрист + 2е,	(7.100)
Sкрист + 4Н2Oжидк = НSО-4 водн + 7Н+водн + 6е,	(7.101)
Sкрист + 4Н2Ожидк = SО2-4 водн + 8Н+водн + 6е.	(7.102)

Поскольку активность кристаллической серы равна единице, каждому из перечисленных уравнений, за исключением уравнения (7.100), на диаграмме Eh - рН соответствует линия, характеризующая соотношение, при котором активность рассматриваемых растворенных компонентов равна заданной величине (10^-1). Таким образом, эти четыре линии и определяют границы поля устойчивости самородной серы. Фиг. 7.17 характеризует устойчивость серусодержащих компонентов при частном значении суммарной активности растворенной серы, равной 10^-1 (величина 10^-1 выбрана в связи с тем, что она приблизительно соответствует активности Н2Sводн в растворе, насыщенном сероводородом при давлении 1 аmм и температуре 25° С).

СООТНОШЕНИЯ УСТОЙЧИВОСТИ ПИРРОТИНА И ПИРИТА

Теперь мы можем определить устойчивость пирротина и пирита по отношению к магнетиту и гематиту в растворах с данной суммарной активностью . растворенной серы. Методики расчета ничем не отличаются от тех, которыми мы пользовались при рассмотрении соотношений сидерита с магнетитом и гематитом. Применяя первый метод, можно рассчитать положение изолиний [Fe²⁺] в равновесии с пиритом и пирротином, а затем определить границы полей устойчивости этих сульфидов по отношению к окислам железа. Последнюю задачу можно решить графически, совмещая две диаграммы с изолиниями [Fе²⁺], рассчитанными одна для равновесия с сульфидами, а другая для равновесия с окислами железа. Вместе с тем для каждого из полей растворенных компонентов можно составить и рассчитать реакции между сульфидами и окислами, а также между самими сульфидами. Этот второй метод мы сейчас и продемонстрируем.

Полагая, что суммарная активность растворенной серы равна 10^-1, рассчитаем границы между полями устойчивости твердых веществ. Результаты вычислений сведены на фиг. 7.18.

Для поля H₂S справедливы следующие равенства:

FеSкрист + Н2Sводн = FеS2 крист + 2Н+водн + 2е,	(7.103)
Eh = -0,133 - 0,059рН - 0,0295 lg 10-1.	(7.104)

По соответствующей линии на диаграмме можно видеть, что в присутствии H₂S пирротин окисляется до пирита ниже границы устойчивости воды. Следовательно, пирротин неустойчив в воде, если активность Н₂S равна 10^-1. Далее

3FеS3 крист + 4Н2Oжидк = Fе3O4 крист + 3Н2Sводн + 2Н+водн + 2е,	(7.105)
Eh = 0,754 - 0,059рН + 0,088 lg 10-1.	(7.106)

Линия, определяемая уравнением (7.106), даже не попадает в поле H₂S, т. е. пирротин в пределах всего поля H₂S более устойчив, чем магнетит. Иначе говоря, активность Н₂S должна быть значительно ниже, чтобы в поле преобладания H₂S появилось поле магнетита.

Теперь рассмотрим реакцию перехода от магнетита к пириту:

3Fе3O4 крист + 6Н2Sводн = 3FеS2 крист + 4Н2Oжидк + 4Н+водн + 4е,	(7.107)
Eh = -0,577 - 0,059рН - 0,088 lg 10-1.	(7.108)

Подобно границе пирротин-пирит (7.104), эта линия располагается значительно ниже границы устойчивости воды, свидетельствуя тем самым о невозможности устойчивого существования магнетита в поле H₂S. Наконец, мы можем написать

Fe2O3 крист + 4Н2Sводн = 2FeS2 крист + 3Н2Ожидк + 2Н+водн + 2е,	(7.109)
Eh = -0,831 - 0,059рН - 0,118 lg10-1.	(7.110)

Если соответствующую линию мы нанесем на диаграмму, то увидим, что реакция (7.109) в поле H₂S также метастабильна. Между прочим, интересно заметить, что реакции H₂S с гематитом и магнетитом, приводящие к образованию пирита, относятся к окислительным; в этом случае восстановление

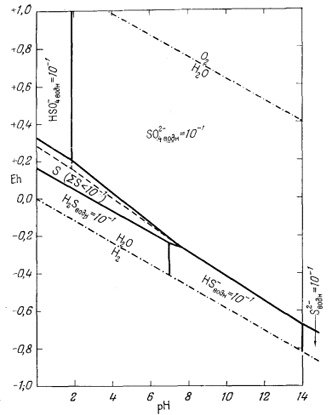Фиг. 7.17. Поля равновесия серусодержащих компонентов в воде при 25° С и 1 атм общего давления для суммарной активности растворенной серы, равной 10-1. В этих условиях самородная сера существует в виде устойчивой фазы. Вдоль штриховой линии в пределах поля серы активности растворенных компонентов равны между собой.

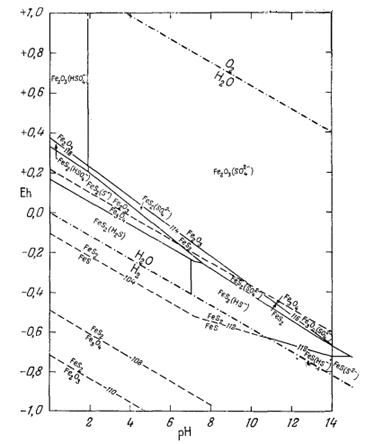Фиг. 7.18. Соотношения устойчивости сульфидов и окислов железа в воде при 25° С и 1 атм общего давления и суммарной активности растворенной серы, равной 10-1. Сплошные линии отвечают устойчивым границам окислов и сульфидов или же границам полей растворенных серусодержащих компонентов; штриховые линии - метастабильные границы. Цифры на линиях соответствуют номерам уравнений в тексте.

железа сильно перекрывается окислением сульфид-иона в сероводороде до дисульфидного иона в пирите.

Итак, мы пришли к выводу, что в поле, где [Н₂S] = 10^-1, устойчивым компонентом оказывается пирит. В поле иона HS^- реакции аналогичны только что рассмотренным, если не считать некоторого изменения в наклоне линий, Здесь следует рассчитать только реакцию между пирротином и пиритом, так как линия, соответствующая этой реакции, может пересечь нижний предел устойчивости воды. Поэтому

FеSкрист + НS-водн = FeS2 крист + Н+водн + 2е,	(7.111)
Eh = -0,340 - 0,0295pH - 0,0295 lg 10-1.	(7.112)

Как следует из фиг. 7.18, граница пирротин - пирит при высоком значении рН (@ 10,6) располагается в пределах поля устойчивости воды, что в значительной мере обусловлено небольшим наклоном линии, соответствующей уравнению (7.112).

На этом основании можно высказать догадку, что поле магнетита будет вытеснено полем пирита. Поэтому попытаемся найти границу между пиритом и гематитом в поле SO^2-₄. Если окажется, что она располагается выше границы магнетит - гематит, то наше предположение подтвердится. Итак, напишем

2FeS2 крист + 19Н2Oжидк = Fе2О3 крист + 4SO2-4 водн + 38Н+водн + 30е,	(7.113)
Eh = 0,380 - 0,075рН + 0,0079 lg 10-1.	(7.114)

Если нанести уравнение (7.114) на диаграмму, то окажется, что вплоть до значения рН=10 отвечающая ему линия будет лежать выше границы гематит - магнетит, показывая тем самым, что в этих пределах (при условии SO^2-₄ = 10^-1) пирит устойчив по отношению к магнетиту. Однако для значений рН, превышающих 10, следует рассмотреть также реакцию перехода пирита в магнетит:

3FeS2 крист + 28Н2Oжидк = Fе3О4 крист + 6SO2-4 водн + 56Н+водн + 44е,	(7.115)
Eh = 0,384 - 0,075рН + 0,0080 lg 10-1.	(7.116)

Если выразить это уравнение графически, то легко можно заметить, что соответствующая ему линия довольно точно совпадает с линией, проведенной по уравнению (7.114). Наконец, остается только определить границу между FeS₂ и Fe₂О₃ в поле иона HSO^-₄. Она характеризуется уравнением

2FeS2 крист +19Н2Oжидк = 4НSO-4 водн + Fе2O3 крист + 34Н+водн + 3Ое,	(7.117)
Eh = 0,366 - 0,067рН + 0,0079 lg10-1.	(7.118)

Теперь, зная положение полей устойчивости всех твердых веществ, можно перейти к расчету активностей ионов, которые находятся с ними в равновесии, и, таким образом, построить окончательную диаграмму для сульфидов и окислов железа. Для полей устойчивости магнетита и гематита изолинии [Fe²⁺] можно перенести непосредственно с фиг. 7.52. Для определения положения изолиний [Fe²⁺] в пределах поля пирита еще раз воспользуемся полями преобладания растворенных серусодержащих компонентов. В поле иона H₂S

2Н2Sводн + Fе2+водн = FеS2 крист + 4Н+водн + 2е,	(7.119)
Eh = 0,057 - 0,118рН - 0,059 lg 10-1 - 0,0295 lg [Fe2+].	(7.120)

В поле иона HSO^-₄

FeS2 крист + 8Н2Oжидк = 2НSO-4 водн + Fе2+водн + 14Н+водн + 14е,	(7.121)
Eh = 0,339 - 0,059рН + 0,0084 lg 10-1 + 0,0042 lg [Fe2+].	(7.122)

В поле иона SO^2-₄

FeS2 крист + 8Н2Oжидк = 2SO2-4 водн + Fе2+водн + 16H+водн + 14е,	(7.123)
Eh = 0,354 - 0,067рН + 0,0084 lg10-1 + 0,0042 lg[Fe2+].	(7.124)

В поле иона HS^-

2НS-водн + Fe2+водн = FeS2 крист + 2Н+водн + 2е,	(7.125)
Eh = - 0,470 - 0,059рН - 0,059 lg 10-1 - 0,029 lg [Fe2+].	(7.126)

В поле самородной серы

FeS2 крист = Fe2+водн + 2Sкрист + 2е,	(7.127)
Eh = 0,340 + 0,0295 lg[Fe2+].	(7.128)

Поскольку во всех уравнениях единственными переменными служат Eh, рН и lg [Fe²⁺], мы можем задаваться произвольными значениями [Fe²⁺] и определять положение соответствующих изолиний в пределах поля пирита. Если все расчеты сделаны правильно, то изолинии [Fe²⁺] в поле пирита точно примкнут к аналогичным изолиниям в полях окислов железа. Диаграммы "растворимости", полученные с помощью рассматриваемого метода, приведены на фиг. 7.19. Изолинии [Fe²⁺] для небольшого поля пирротина можно определить из единственной реакции

FеSкрист + Н+водн = Fе2+водн + HS-водн,	(7.129)
lg[Fe2+] = -4,4 - pH - lg 10-1.	(7.130)

Полученная диаграмма отражает некоторые интересные и, по-видимому, не вызывающие сомнений соотношения. Прежде всего она показывает, что если за критерий устойчивости принять активность растворенного железа, равную 10^-6, то при величинах рН > 3 пирит не сможет окислиться с выделением серы. При подобных значениях рН и величине окислительного потенциала, при котором происходит окисление пирита, сера не может стать твердой фазой. Наряду с этим следовало бы ожидать, что менее устойчивый марказит будет отдавать серу при более высоких значениях рН. Этим, по-видимому, и объясняется, почему марказит отдает серу, идущую на окисление через посредство солей Трехвалентного железа, чего не происходит в случае пирита, за исключением средне высокой концентрацией таких солей. Кроме того, преимущественное тяготение поля устойчивости пирита к кислой среде со средними значениями Eh служит ответом на вопрос,почему в противоположность окисляющим кислотам неокисляющие неорганические кислоты не оказывают воздействия на пирит.

Наличие поля "растворимости" пирита в условиях кислой восстановительной среды указывает на возможность разложения пирита в кислом растворе под воздействием восстановителей. Этот вывод можно проверить экспериментально. Наконец, большой геологический интерес представляют соотношения между пиритом, пирротином и магнетитом. Ассоциация этих трех минералов характерна для руд высокотемпературных месторождений. Как было показано, при комнатной температуре подобная трехфазовая ассоциация может существовать только при рН > 14, если сумма растворенной серы равна 10^-1. Сопоставление этих данных наводит на мысль, что условия устой-

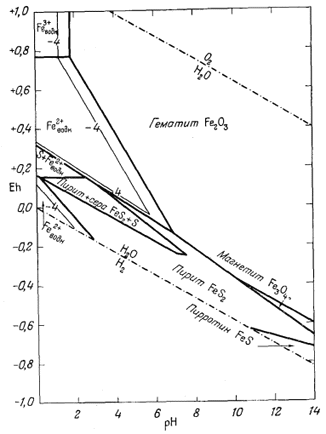Фиг. 7.19. Соотношения устойчивости окислов и сульфидов железа в воде при 25° С и 1 атм общего давления и активности растворенной серы, равной 10-1. Границы между ионами и твердыми веществами проведены при активности растворенного железосодержащего компонента, равной 10-6. Цифра -4 обозначает логарифм активности ионов железа, который использован здесь с целью показать характер изменения "растворимости".

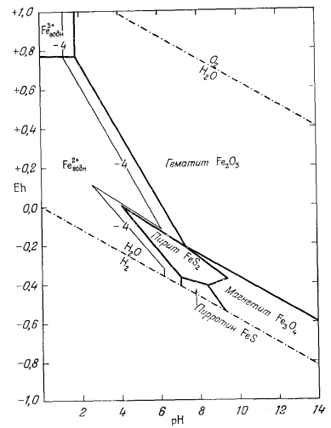Фиг. 7.20. Соотношения устойчивости окислов и сульфидов железа в воде при 25° С и 1 атм общего давления при условии, если SS = 10-6. Интересно, что поле сульфидов сокращается, а в виде устойчивой фазы при средних значениях pH и в сильно восстановительной обстановке появляется FeS. Заметно также расширение области "кислотной растворимости" на более широкий диапазон Eh.

чивости данного парагенезиса при повышении температуры смещаются в сторону более низких значений рН.

Фиг. 7.20 характеризует изменения, которые вызывает снижение суммарной активности растворенной серы до 10^-6. Как и следовало ожидать, поля устойчивости сульфидов заметно сокращаются в размерах. В условиях сильно восстановительной среды и при рН @ 8 в качестве устойчивой фазы появляется пирротин, а область "растворимости" заметно расширяется в сторону повышения кислотности. На основании анализа двух последних диаграмм можно убедиться, что устойчивые сульфиды впервые образуются при значениях рН, близких к нейтральным, при условии, что в системе появляются ничтожные количества двухвалентной серы (вероятно производимой живыми организмами).

СООТНОШЕНИЯ МЕЖДУ МИНЕРАЛАМИ ЖЕЛЕЗА В ВОДЕ,
СОДЕРЖАЩЕЙ CO₂ И СЕРУ

Весьма интересна в геологическом отношении природная система, в которой принимают участие растворенный карбонат и сера. Так, осадочные железные руды характеризуются наличием окислов железа, карбонатов, сульфидов и силикатов. Если мы попытаемся использовать для изучения подобной системы диаграммы Eh - рН, то даже по исключении из нее на время силикатов в ней все равно останется слишком большое число переменных величин и поэтому она не сможет наглядно свидетельствовать о влиянии непрерывного изменения активности серусодержащих компонентов. Вместе с тем любую систему, характеризующуюся постоянными значениями SCO₂ и SS, можно представить в двумерной диаграмме Eh - рН. Кроме того, можно построить частные диаграммы - одну для произвольного значения SСО₂, другую для произвольного значения SS; эти диаграммы можно совместить и определить таким образом положение полей устойчивости минералов в общей системе.

Например, фиг. 7.11 характеризует соотношения устойчивости между гематитом, магнетитом и сидеритом при SСO₂ = 10^-2, а на фиг. 7.20 показаны соотношения между гематитом, магнетитом, пиритом и пирротином при SS = 10^-6. Если совместить диаграммы сульфидов и карбонатов, то можно сразу же обнаружить, что на диаграмме SS активность растворенного. железа в равновесии с перечисленными минералами повсюду меньше, чем на диаграмме SСО₂. Другими словами, при условии SS = 10^-6 и SСO₂ = 10^-2 устойчивы только окислы и сульфиды железа, а сидерит неустойчив. При этом необходимо подчеркнуть, что наше рассуждение относилось к равновесной системе, ибо хорошо известно, что при низкой температуре сульфат-ион восстанавливается чрезвычайно медленно, если только в этом процесса не участвуют живые организмы.

Фиг. 7.21 построена для равновесных соотношений при SСO₂ = 10⁰ и SS = 10^-6. Ее анализ показывает, что сидерит будет обладать значительным полем устойчивости только в условиях очень высокой активности растворенного карбоната и чрезвычайно низкой активности восстановленной серы. В подобных условиях поле устойчивости пирротина исчезает, но остается большое поле устойчивости пирита. Интересно, что в отмеченных условиях наличие сидерита может служить критерием резко восстановительной или же умеренно восстановительной обстановки во многих железных рудах, а также, по-видимому, отсутствия заметных концентраций двухвалентной серы и относительно высокой активности растворенной углекислоты,

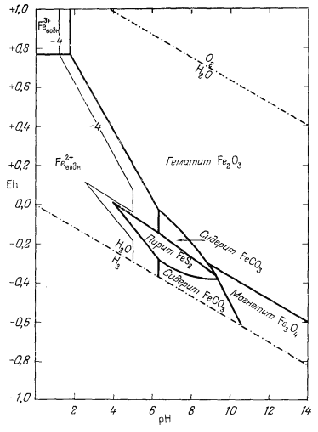Фиг. 7.21. Соотношения устойчивости окислов, сульфидов и карбоната железа в воде при 25° С и 1 атм общего давления. Сумма растворенной серы равна 10-6, сумма растворенного карбоната равна 100. Интересно исчезновение поля FeS за счет поля FеСО3 в сильно восстановительной обстановке, а также значительная устойчивость пирита в присутствии малых количеств растворенной серы.

ВЛИЯНИЕ ПРОЧИХ КОМПОНЕНТОВ, НАПРИМЕР КРЕМНЕЗЕМА, НА
СООТНОШЕНИЯ В СИСТЕМЕ ОКИСЛОВ И СИЛИКАТОВ ЖЕЛЕЗА

К сожалению, в настоящее время мы не располагаем термохимическими данными, достаточными для того, чтобы разобраться в сложной обстановке отложения минералов железа осадочного происхождения при участии значительных количеств кремнезема. Значение свободной энергии известно только для метасиликата железа FeSiO₃, который является условным заменителем природных соединений - железистых хлоритов и шамозитов. И тем не менее нам придется рассматривать методику проведения расчетов для силикатных соединений на примере FеSiO₃.

Одно из достоинств диаграмм устойчивости, которое часто недооценивается, заключается в возможности с их помощью изображать системы с большим числом переменных. Обычно все же стараются ограничиться двумя или тремя переменными и показать их действие в качестве непрерывных функций. Однако если задаваться вполне конкретными значениями каждой из переменных и строить соответствующие частные диаграммы, то можно без особых затруднений оперировать пятью или шестью переменными. Построение диаграмм, которые охватывали бы такой порядок интересующих нас переменных, представляет собой трудоемкую работу по построению многочисленных, но необходимых частных диаграмм. Однако этим в настоящее время и исчерпываются все трудности, связанные с их получением.

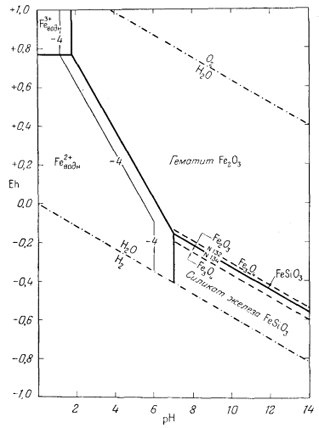Фиг. 7.22. Соотношения устойчивости окислов и мета-силиката железа при 25° С и 1 атм общего давления в присутствии воды. Предполагается, что в системе участвует твердое силикатное стекло. Цифры на линиях соответствуют порядковым номерам уравнений в тексте. Цифра -4 на тонких линиях - логарифм суммы растворенного железа в равновесии с твердыми веществами.

Возвратимся к проблеме силикатов железа. Ее можно решить при допущении, что в системе окислов и силикатов железа в виде твердой фазы присутствует кремнезем. Поскольку имеются многочисленные доказательства того, что кремнезем в форме опала находился в первичной ассоциации со всеми прочими минералами железа, мы можем с полным основанием считать, что аморфный кремнезем (силикатное стекло) - неизменный спутник минералов железа в осадочных железистых рудах. Теперь, если мы признаем справедливость подстановки метасиликата железа вместо реальных силикатов, обнаруживаемых в железных рудах, мы можем написать

3FеSiO3 крист + Н2Ожидк = Fе3O4 крист + 3SiO2 стекло + 2H+водн + 2е,	(7.131)
Eh = 0,272 - 0,059 рН.	(7.132)

Уравнение (7.132) отражено на фиг. 7.22; оказывается что граница между FеSiO₃ и Fе₃O₄ лежит выше границы Fe₃O₄ - Fe₂O₃. Другими словами, магнетит неустойчив относительно метасиликата железа, если в системе присутствует силикатное стекло или же система насыщена в отношении аморфного кремнезема. Определим границу между FеSiO₃ и Fe₂O₃:

2FeSiO3 крист + Н2Ожидк = Fe2O3 крист + 2SiO2 стекло + 2H+водн + 2е,	(7.133)
Eh = 0,258 - 0,059 рН.	(7.134)

Линия, соответствующая последнему уравнению, располагается выше линии Fе₃O₄ - Fe₂O₃, а это свидетельствует о том, что в присутствии силикатного стекла в качестве твердых фаз могут образоваться силикат железа и гематит. Тогда для поля устойчивости FeSiO₃ мы вправе написать

FeSiO3 крист + 2H+водн = Fе2+водн + SiO2 стекло + Н2Ожидк	(7.135)
lg[Fe2+] = 8,03 - 2 рН.	(7.136)

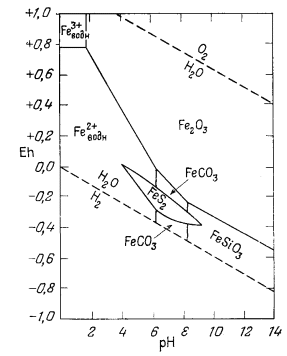Ф и г. 7.23. Соотношения устойчивости окислов, карбонатов, сульфидов и силикатов железа при 25° С и 1 атм общего давления в присутствии воды. Прочие условия: сумма СО2 равна 100; сумма серы равна 10-6; присутствует аморфный кремнезем. Эта диаграмма приводится с целью показать возможность изображения многокомпонентной системы в координатах Eh - рН, если задаваться произвольными величинами для каждой из переменных.

Подставив численные значения [Fe²⁺], равные 10^-6 и 10^-4, мы получаем возможность построить диаграмму "растворимости" для системы силикат железа - окислы железа. Она показывает, что в системе, состоящей только из окислов железа и силиката железа, в присутствии аморфного кремнезема магнетит как твердая фаза не участвует. Несомненно, что реальные силикаты железа, входящие в состав первичных железных руд, в определенных условиях более устойчивы, чем чистое соединение FeSiO₃. Однако использование в наших расчетах даже FeSiO₃ позволяет нам прийти к выводу, что из придонных вод, насыщенных относительно аморфного кремнезема, будет образовываться силикат железа, а не магнетит, в случае если количество растворенного кремнезема окажется достаточным для того, чтобы связать все имеющееся железо. Вместе с тем общие условия устойчивого существования метасиликата двухвалентного железа и магнетита удивительно близки.

Можно разыграть массу утонченных вариантов при определении устойчивых соотношений для различных значений суммы растворенного карбоната, суммы растворенной серы и суммы растворенного кремнезема при бесконечно меняющихся условиях. На фиг. 7.23 приведена сводная диаграмма для частных условий, согласно которым SСO₂ = 10⁰, SS = 10^-6, a SSiO₂ равновесна в отношении силикатного стекла (аморфного кремнезема). Эта диаграмма была построена путем наложения диаграмм фиг. 7.22 и 7.21.

Совершенно очевидно, что в случае первичных осадочных железных руд сидеритовая фация образуется при высокой концентрации растворенного CO₂ и при удалении из системы сульфидной серы; силикатная фация образуется вследствие удаления серы и снижения концентрации CO₂, причем избыточный SiO₂ идет на образование роговика^{1 (стр.195)}; магнетитовая фация образуется при уменьшении концентрации серы, CO₂ и при сохранении концентрации кремнезема на уровне, не превышающем насыщение раствора в отношении аморфного кремнезема.

ПЕРЕХОД ОТ ДИАГРАММ ПАРЦИАЛЬНЫХ ДАВЛЕНИЙ К
ДИАГРАММАМ Eh - рН

На приведенных в гл. 6 диаграммах соотношения между окислами, сульфидами и карбонатами были даны в виде функций P_O2, P_CO2 и P_S2. Особенно интересна с геологической точки зрения система с окислами и сульфидами меди и железа (фиг. 6.16). Натарайану (Natarajan, неопубликованная работа, Гарвардский университет, 1958) удалось перейти от таких диаграмм к диаграммам Eh - рН. Как указывалось выше, значения Р_O2 можно наносить на диаграммы Eh - рН в виде изолиний (фиг. 7.1). При данной сумме растворенной серы на ту же диаграмму можно нанести и изолинии P_S2 Например, если SS = 10^-1, то для поля, в котором преобладающим компонентом является H₂S (фиг. 7.17), мы можем написать

2Н2Sводн = S2 газ + 4Н+водн + 4е.

(7.137)

При условии что H₂S = 10^-1, этой реакции соответствует следующее уравнение Eh и рН:

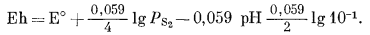(7.138)

По этому уравнению можно определять положение изолиний P_S2 любой заданной величины в пределах поля преобладания H₂S. Поскольку на фиг. 6.16 все соотношения показаны через P_S2 и P_O2 , от нее можно перейти к диаграмме Eh - рН при условии, что сумма растворенной серы постоянна. Соотношения между сульфидами меди и железа, изображенные на фиг. 7.24 и 7.25, справедливы соответственно для SS = 10^-1 и SS = 10^-4. Они характеризуют положение полей устойчивости для большого числа соединений в условиях, близких к природным процессам окисления и вторичного обогащения медных руд.

ВЫВОДЫ ПО РАЗДЕЛУ, ПОСВЯЩЕННОМУ СООТНОШЕНИЯМ МЕЖДУ
МИНЕРАЛАМИ ЖЕЛЕЗА

Только что законченный подробный разбор соотношений между минералами железа был проделан нами в надежде, что продемонстрированная методика окажется полезной тому, кто с ее помощью захочет разобраться в аналогичных соотношениях для какого-либо другого элемента. Мы не останавливались на возможности использования полученных соотношений для объяснения геологических явлений, боясь прервать нить последовательного изложения методической стороны построения диаграмм устойчивости. Однако диаграммы, которые отражают взаимоотношения между окислами, карбонатами, сульфидами и силикатами железа, настолько хорошо соответствуют условиям нахождения этих минералов в природе, что всякие слова зачастую

1 (стр.195) Термин "роговик" (chert) здесь используется при допущении, что кремнистые прослойки в железистых формациях, ныне представленные кристаллическим кварцем, первоначально были сложены полимеризованным аморфным кремнеземом - опалом.

просто излишни. Кроме того, мы показали, что для одних только соединений железа можно было бы построить бесчисленное количество диаграмм, и любой исследователь, интересующийся частными условиями, может изучить их в той же последовательности, как это сделано при построении предложенных здесь графиков.

ДИАГРАММЫ Eh - рН ДЛЯ ДРУГИХ ЭЛЕМЕНТОВ

В настоящем разделе приводятся диаграммы Eh - рН для различных элементов; в подписях к этим диаграммам указаны конкретные условия, для которых производились вычисления. Геологическая интерпретация некоторых приведенных здесь диаграмм будет дана в последней главе. Большинство диаграмм читатель должен разобрать самостоятельно, сообразуясь со своим личным опытом, поскольку подобный разбор в пределах настоящей работы невозможен без значительного увеличения объема текстовой части. Мы не теряем надежды, что та детальность, с которой были рассмотрены диаграммы для железа, оказалась достаточной и читатель понял, что данные диаграммы справедливы только для тех ограниченных условий, в отношении которых производились расчеты. Например, существует тенденция изображать соотношения между карбонатами, окислами и сульфидами железа без ссылки на использование в вычислениях значения SS и SCO₂. Пренебрежение конкретными условиями делает в значительной степени невозможным применение подобных диаграмм.

Приводимые здесь диаграммы характеризуют соотношения для металлов в воде, насыщенной кислородом; рассчитаны они различными исследователями, на которых сделаны соответствующие ссылки. Следует еще раз подчеркнуть, что подробный расчет каждой из них наряду с многочисленными диаграммами, охватывающими различные варианты условий, можно найти в соответствующих выпусках "Cebelcor", список которых приведен в конце настоящей главы. На основании данных, имеющихся в этих выпусках, и произведены расчеты всех диаграмм настоящего раздела.

ФИГ. 7.24 И 7.25

Эти диаграммы с наибольшей доступной в настоящее время точностью отражают соотношения в системе медь - железо - вода - сера при 25° С и 1 атм общего давления в присутствии растворенной серы с постоянной активностью. Они были построены с целью изучения и интерпретации соотношений, господствующих в зонах окисления и вторичного обогащения рудных месторождений. На первый взгляд диаграммы кажутся сложными, но уже после небольшого их изучения картина становится ясной. Сульфиды меди и железа отделены от окислов тех же металлов четко выраженным поясом, протягивающимся от Eh, равного приблизительно 0,3 при рН = 0, вправо вниз с наклоном около 60 мв на единицу рН. Один только халькозин (Cu₂S) проникает заметно выше этой границы, что согласуется с образованием зоны халькозина в результате вторичного обогащения медных руд. Заметим, что окисление в кислой обстановке должно приводить к образованию (в условиях равновесия) достаточно высокой концентрации ионов Сu²⁺ и Fe²⁺ или при несколько меньшей кислотности иона Сu²⁺ и твердого Fe₂O₃ (или Fe₂O₃ЧH₂O). Отсюда становится ясной и причина разделения железа и меди в процессах окисления. Среди вторичных продуктов легко может оказаться и самородная медь, которая образуется при нейтрализации нисходящих медьсодержащих растворов. Для осаждения заметных количеств меди из раствора в виде куприта и тенорита необходимо довольно высокое значе-

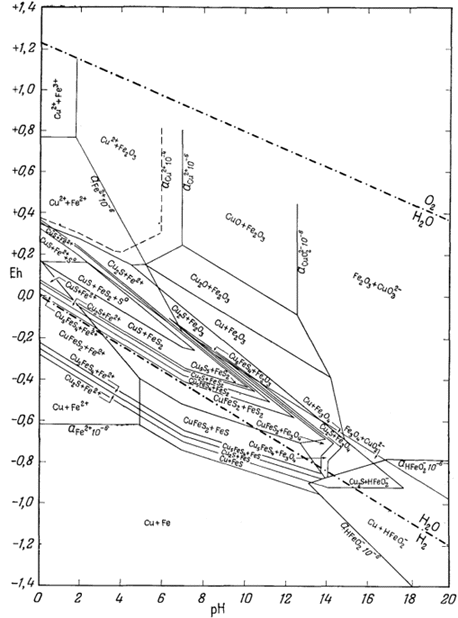Фиг. 7.24. Система Сu - Fe - S - О - Н (не полностью) при 25° С и 1 атм общего давления. Сумма растворенной серы равна 10-1 М (по Натарайану и Гаррелсу).

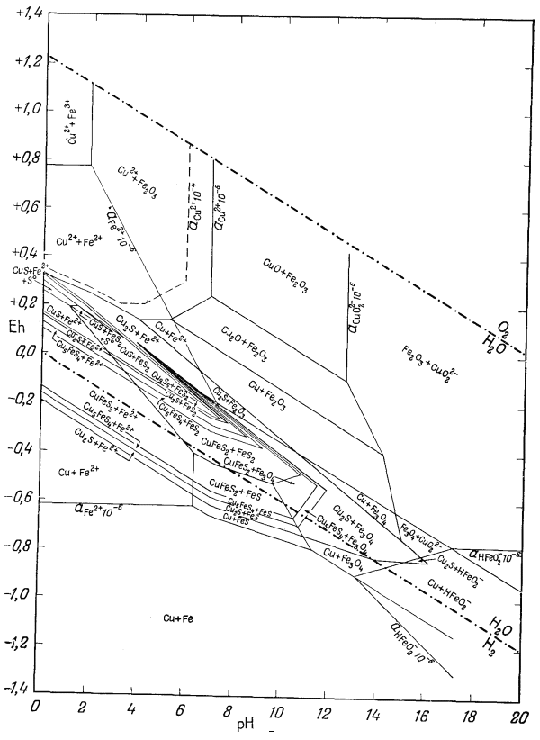Фиг. 7.25. Система Сu - Fe - S - О - Н (не полностью) при 25° С и 1 атм общего давления. Сумма растворенной серы равна 10-4 М (по Натарайану и Гаррелсу).

 

ние рН. На основании данных фиг. 7.24 и 7.25 можно также вывести ряд других интересных закономерностей. Диаграммы составлены в 1957 г. Ната-райаном и Гаррелсом при участии сотрудников из Комитета по экспериментальной геологии при Гарвардском университете.

ФИГ. 7.26а -7.26д

На этой серии диаграмм показаны равновесные соотношения между соединениями свинца в воде при 25° С и 1 атм общего давления в присутствии СО2 или серы. Здесь же приведены диаграммы для комбинированных условий.

Из данных фиг. 7.26а следует, что при условии невысокого парциального давления СО₂ поля устойчивости различных свинцовых окислов, за исключением небольшого поля PbO₂, исчезают. Это позволяет рассматривать минерал PbO₂ (платтнерит) в качестве чувствительного индикатора щелочной окислительной среды.

Фиг. 7.26б отличается от предыдущей фигуры более высокой суммой растворенного CO₂; различие между этими двумя диаграммами сказывается в появлении среди устойчивых твердых фаз Рb₃(ОН)₂(СО₃)₂. На диаграмме проведены изолинии активности ионов для значений, превышающих 10^-4, благодаря чему уточняются условия нахождения в этой системе фаз Рb₃O₄ и РbО. Соединение Рb₃(ОН)₂(СO₃)₂ (гидроцеруссит), по-видимому, служит хорошим индикатором щелочной среды. Характерно, что в подобных карбонатных водах сохраняется поле устойчивости самородного свинца.

Фиг. 7.26в иллюстрирует влияние прибавления серы к системе вода - окисные соединения свинца. Эта диаграмма составлена для активности серы, равной 10^-5; оказывается, что уже в этих условиях большим полем устойчивости обладает галенит, причем наблюдаются широкие пределы устойчивости англезита. Обратите внимание, что на этой диаграмме за границу между ионами и твердыми веществами принята изолиния со значением активности серы, равным 10^-2. Если бы, как обычно, граница проводилась по изолинии 10^-6, то сразу исчезли бы поля PbSO₄ и РbО, ибо изолинии 10^-6 Pb²⁺ и 10^-6 НРbО^-₂ сходятся при рН 9,3. Между прочим, даже при такой низкой суммарной активности растворенной серы, как 10^-5, галенит, согласно диаграмме, почти полностью вытесняет поле самородного свинца.

На фиг. 7.26г совмещено влияние СО₂ и серы; эта диаграмма характеризует систему с условиями, близкими к условиям окисления на земной поверхности. Суммарная активность серы высока (10^-1), а Р_CO2 приблизительно равно атмосферному (10^-4). Судя по диаграмме устойчивости, в таких условиях свинец нерастворим: активность его ионов превышает 10^-6 только в очень щелочной или очень кислой среде. Между прочим, эта диаграмма упрощена: она характеризует соотношения только между главными, фактически наблюдаемыми минералами - галенитом, церусситом и англезитом; платтнерит обладает небольшим полем в весьма необычных условиях.

Фиг. 7.26д представляет собой вариант фиг. 7.26г; она отвечает таким условиям, которые могут встретиться в зоне окисления галенитового месторождения, изолированного от атмосферы, но отличающегося достаточно высокой активностью растворенных СО₂ и серы. Благодаря тому что СО₂ обладает постоянной суммарной активностью, вновь появляется гидроцеруссит, который при высоком значении рН может успешно конкурировать с обычным карбонатом. Как было показано выше, при постоянном Р_CO2 сумма растворенного карбоната возрастает с увеличением рН, в связи с чем РbСО₃ остается устойчивой твердой фазой. Анализ фиг. 7.26г и 7.26д позволяет сделать еще один интересный вывод: галенит не может окисляться и выделять серу при значениях рН, превышающих примерно 2; но, как только

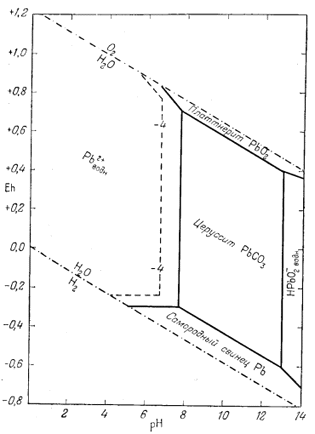Фиг. 7.26а. Соотношения устойчивости окислов и карбонатов свинца в воде при 25° С и 1 атм общего давления и PCO2, равном 10-4. Границы полей твердых веществ проведены при суммарной активности ионов, равной 10-4; проведена также изолиния активности, равной 10-4 (по Мак-Интайру).

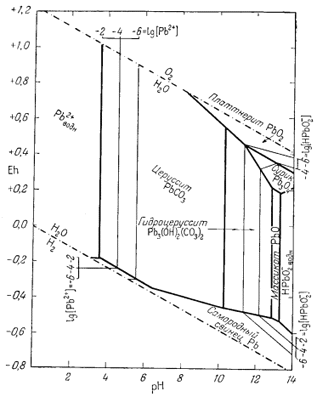Фиг. 7.26б. Соотношения устойчивости между соединениями свинца в воде при 25° С и 1 атм общего давления. Сумма растворенных карбонатных компонентов равна 10-1,5 (по Мак-Интайру).

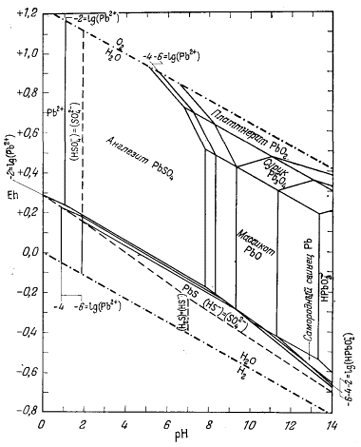Фиг. 7.26в. Соотношения устойчивости между соединенниями свинца в воде при 25° С и 1 атм общего давления. Сумма растворенной серы равна 10-5 (по Мак-Интайру).

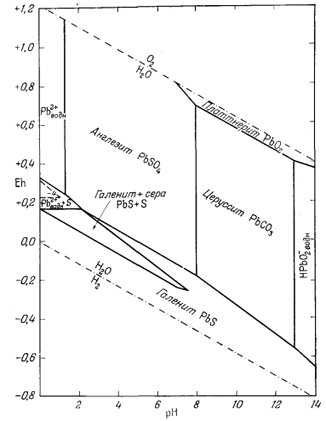Фиг. 7.26г. Соотношения устойчивости между соединенниями свинца в воде при 25° С и 1 атм общего давления и PCO2, равном 10-4. Сумма растворенной серы равна 10-1. Границы полей твердых веществ проведены при суммарной активности ионов, равной 10-4. Пунктирная линия - изолиния активности растворенных компонентов свинца, равной 10-4 (по Мак-Интайру).

кислотность среды превысит это значение, поле самородной серы становится больше поля PbS и возникает, кроме того, небольшое поле PbSO₄ + S.

Итак, мы приходим к выводу, что диаграммы Eh - рН имеют большое значение при рассмотрении поведения минералов свинца и что некоторые

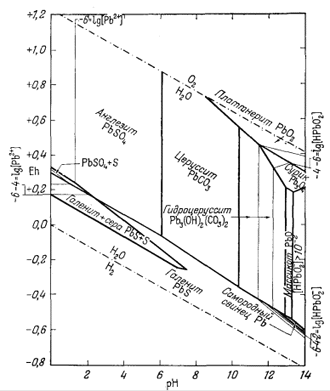Фиг. 7.26ц. Соотношения устойчивости между соединениями свинца в воде при 25° С и 1 атм общего давления. Сумма растворенной серы равна 10-1,5; сумма растворенных карбонатных компонентов равна 10-1 (по Май-Интайру).

из минералов можно использовать в качестве индикаторов среды. Приведенные здесь диаграммы были составлены в 1957 г. Мак-Интайром, сотрудником геологического отделения Массачусетского технологического института, и лишь незначительно дополнены авторами.

ФИГ. 7.27а -7.27б

Здесь рассматриваются соотношения между минералами меди при 25° С и 1 атм общего давления в присутствии воды.

Фиг. 7.27а иллюстрирует соотношения в системе медь - кислород - вода; обращает на себя внимание большое поле устойчивости самородной меди^{1 (стр.202)}, а также наличие поля растворимости меди (в виде иона двухвалентного металла) в кислой среде. Если бы за границу полей ионов мы приняли активность, равную 10^-7, то на диаграмме появилось бы поле иона Сu⁺ в участке, обозначенном соответствующим индексом в скобках. Своеобразное

1 (стр.202) Это прекрасно согласуется с встречающимся в природе цеолитным типом месторождений самородной меди (тип озера Верхнего).- Прим. ред.

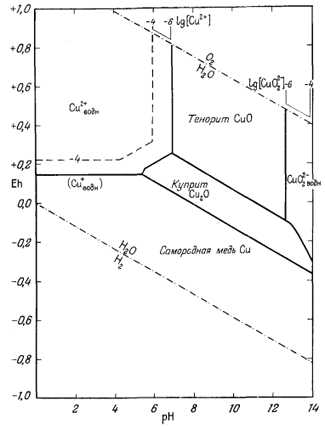Фиг. 7.27а. Соотношения устойчивости между соединениями меди в системе Cu - H2O - O2 при 25° С, 1 атм общего давления (по Андерсону).

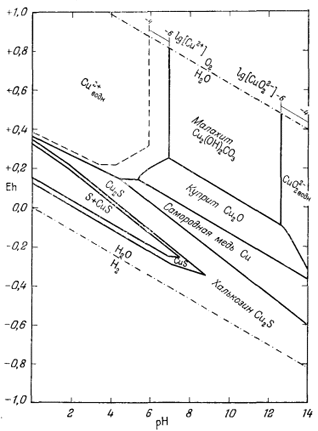Фиг. 7.27б. Соотношения устойчивости между соединениями меди в системе Cu - H2O - O2 - S - CO2 при 25° С, 1 атм общего давления и PCO2, равном 10-3,5. Сумма растворенной серы равна 10-1 (по Андерсону).

искривление границы между Cu₂O и полем иона Сu²⁺ обусловлено существенным влиянием, которое оказывает ион Сu²⁺ на суммарную активность ионов. При комнатной температуре амфотерные свойства меди заметно не проявляются; существование значительных концентраций иона СuO^2-₂ отмечается только при величинах рН, намного превышающих обычное значение рН природных вод. Если медь по ее инертности можно сравнивать со свинцом, кобальтом и никелем, то из всего сказанного становится ясным, почему самородная медь встречается значительно чаще.

На фиг. 7.276 отражены изменения в системе, происходящие при добавлении к ней CO₂ (Р_CO2 = 10^-3,5) и серы (SS = 10^-1). Нетрудно заметить, что на этой диаграмме малахит занимает поле тенорита, которое имелось на фиг. 7.27а. При более высоком значении Р_CO2 поле малахита должно было бы расшириться еще больше и вытеснить поле куприта. Даже при столь высокой концентрации растворенной серы имеется хорошо выраженное поле самородной меди. Поле сульфидов, как видно из диаграммы, глубоко проникает в пределы кислой среды при восстановительной обстановке. Этим и объясняется осаждение халькозина при соприкосновении кислых медьсодержащих растворов с сульфидами в восстановительной обстановке. Понятно также, что халькозин не может окисляться с образованием самородной серы, поскольку сера не может существовать совместно с халькозином.

Эти две диаграммы составлены в 1958 г. Джеймсом Андерсеном, сотрудником геологического отделения Гарвардского университета.

ФИГ. 7.28а -7.28б

Здесь исследованы соотношения между марганцевыми минералами в воде, содержащей CO₂ и серу, при 25° С и 1 атм общего давления.

Фиг. 7.28а характеризует соотношения устойчивости между окислами и карбонатом марганца при условии, что сумма растворенной CO₂ равна 10^-1,4: в первом приближении можно считать, что вначале система была насыщена CO₂ при давлении 1 атм, после чего доступ этого газа прекратился. Бросается в глаза, что поле карбоната марганца (родохрозита) заметно больше поля сидерита в аналогичных условиях. В отсутствие СО₂ устойчивость более высоковалентных окислов и гидроокиси марганца повышается с увеличением окислительного потенциала. Не удивительно, что гидроокись марганца (пирохроит) - чрезвычайно редкий минерал: для его образования необходима щелочная восстановительная среда и практически полное отсутствие СО₂. Как и для железа, амфотерные свойства марганца не играют заметной роли в природных условиях. Оба иона - МnO^2-₂ и MnO^-₄ - неустойчивы в отношении воды; ион МnO^2-₄ появляется только в пределах небольшого поля в условиях щелочной окислительной среды. В связи с этой особенностью можно напомнить, что раствор перманганата калия в течение нескольких месяцев постепенно разлагается с образованием МnО₂. Этот факт свидетельствует также и о том, что метастабильность может появиться через значительный промежуток времени.

По данным фиг. 7.28б установлены две новые важные закономерности. В этом случае система открыта для CO₂ (Р_CO2 = 10^-4 атм), и, как обычно, поле карбоната вытесняет поле двухвалентного окисла или гидроокисла, что обусловлено увеличением активности ионов СO^2-₃ и ОН^- с повышением рН. Характерны также небольшие размеры поля алабандина (MnS) даже при довольно высокой активности растворенной серы (10^-1). Так как в большинстве случаев морская среда становится восстановительной, в ней появляется двухвалентная сера, а рН понижается до 6,5 - 7,0. В таких условиях марганец начинает переходить в раствор или выпадать в осадок в виде карбоната. Для образования же алабандина необходима необычная реакция

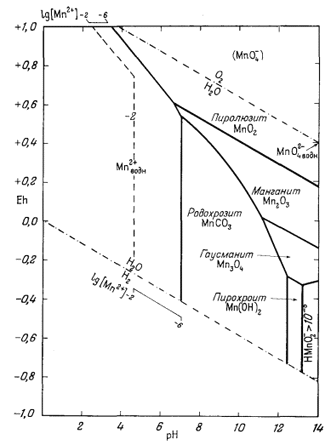Фиг. 7.28а. Соотношения устойчивости между некоторыми соединениями марганца в воде при 25° С и 1 атм общего давления. Сумма растворенных карбонатных компонентов равна 10-1,4 (по Гоше).

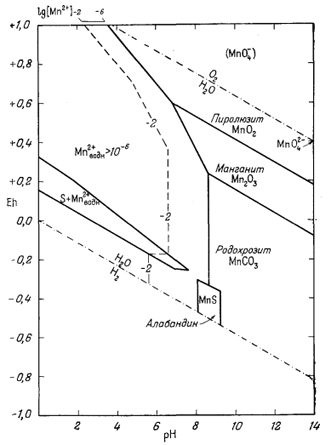Фиг. 7.28б. Соотношения устойчивости между некоторыми соединениями марганца в воде при 25° С, 1 атм общего давления, и PCO2, равном 10-4. Сумма растворенной серы равна 10-1 (по Гоше).

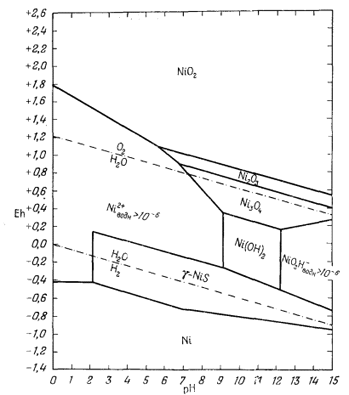Фиг. 7.29а. Соотношения устойчивости между некоторыми соединениями никеля в воде при 25° С и 1 атм общего давления. Сумма растворенной серы равна 10-5 (по Энтони).

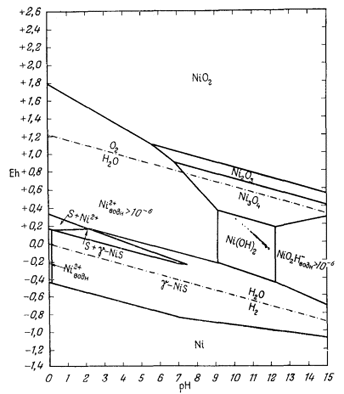Фиг. 7.29б. Соотношения устойчивости между некоторыми соединениями никеля в воде при 25° С и 1 атм общего давления. Сумма растворенной серы равна 10-1 (по Энтони).

(производящая ионы ОН^-). Этот вывод вполне согласуется с известной нам малой распространенностью алабандина в природных ассоциациях.

Рассмотренные диаграммы составлены в 1957 г. Эдвином Гоше, сотрудником геологического отделения Гарвардского университета.

ФИГ. 7.29а -7.29в

Соотношения в системах с участием никеля и воды при 25° С и 1 атм общего давления с добавлением серы или СО₂.

Как следует из данных фиг. 7.29а ^{1 (стр.207)}, при суммарной активности растворенной серы, равной 10^-5, сульфид никеля устойчив в восстановительной

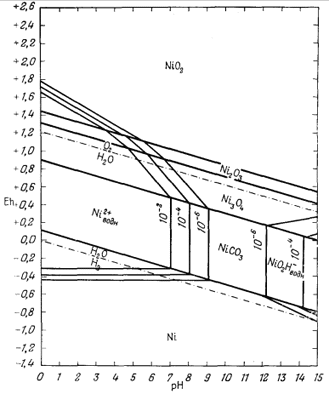Фиг. 7.29в. Соотношения устойчивости между некоторыми соединениями никеля в воде при 25° С, 1 атм общего давления и РCO2 , равном 10-0,8 (по Энтони).

обстановке в широких пределах значений рН. В то же время окислы и гидроокислы никеля довольно хорошо растворимы, на что указывают большие размеры полей иона Ni²⁺ в кислой среде и иона NiO₂H^- в щелочных условиях. В общем поведение никеля очень напоминает поведение железа; единственное различие заключается в том, что Ni(OH)₂ характеризуется значительным полем устойчивости, а в системе с железом поле Fe(ОН)₂ совершенно отсутствует. К сожалению, нам неизвестна свободная энергия образования NiS₂ - аналога пирита, но если бы это соединение было устойчиво, то его поле располагалось бы между полями NiS и Ni(ОН)₂.

1 (стр.207) Эта диаграмма с некоторыми уточнениями приведена в более новой статье Летов-ского, Серкиса и Немеца [Econ. Geol., 61, № 7 (1966)].- Прим. ред.

На фиг. 7.29б показано влияние повышения суммарной активности серы, выражающееся в появлении поля самородной серы и расширении области существования NiS.

По фиг. 7.29в можно судить о влиянии CO₂ на устойчивость окислов никеля. Избранная величина Р_CO2 оказалась как раз достаточной, чтобы уничтожить поле Ni(ОН)₂. Этот факт свидетельствует о том, что карбонат никеля служит хорошим индикатором на СО₂, так как для его устойчивого существования требуется более высокое значение Р_CO2, чем значение Р_CO2 в атмосфере. На этой же диаграмме проведены изолинии активности ионов. Характерно, что самородный никель, как и свинец, обладает небольшим полем устойчивости в воде и этим отличается от железа. Вместе с тем даже ничтожное добавление к раствору серы исключает возможность устойчивого существования почти всех рассматриваемых металлов в самородном состоянии.

Последние три диаграммы подготовлены в 1957 г. Джоном Энтони, сотрудником геологического отделения Гарвардского университета.

ФИГ. 7.30а -7.30в

Соотношения устойчивости кобальтовых соединений в воде при 25° С и 1 атм общего давления в присутствии СО₂ и серы.

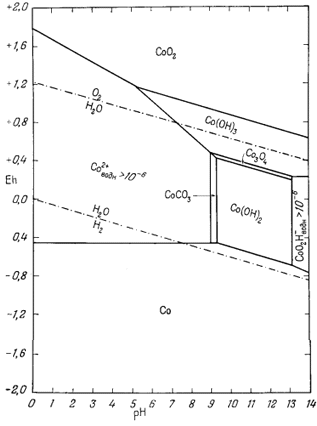Фиг. 7.30а. Соотношения устойчивости между некоторыми соединениями кобальта в воде при 25° С и 1 атм общего давления. Сумма растворенных карбонатных компонентов равна 10-4,9 (по Барнсу).

Из фиг. 7.30а видно, что СоСО₃ в отличие от карбоната никеля становится устойчивым относительно Со(ОН)₂ уже при очень низком содержании в сис-

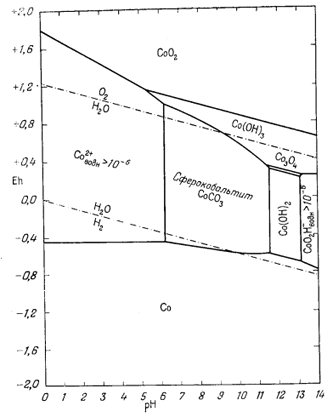Фиг. 7.30б. Соотношения устойчивости между некоторыми соединениями кобальта в воде при 25° С и 1 атм общего давления. Сумма растворенных карбонатных компонентов равна 10-1,5 (по Барнсу).

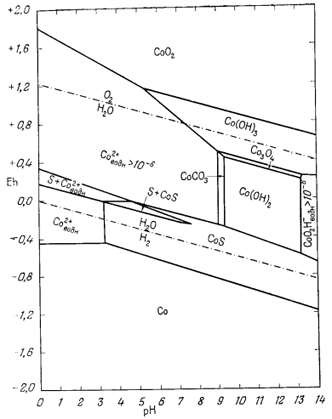Фиг. 7.30в. Соотношения устойчивости между некоторыми соединениями кобальта в воде при 25° С и 1 атм общего давления. Сумма растворенных карбонатных компонентов равна 10-4,9; сумма растворенной серы равна 10-1 (по Барнсу).

теме карбонатных компонентов. На этом основывается разделение никеля и кобальта в различных схемах химического анализа; CoCO₃ можно селективно осадить путем контролируемой карбонатизации раствора. Однако общее сходство поведения кобальта и никеля поразительно ^{1 (стр.210)}.

Фиг. 7.30б свидетельствует о значительном увеличении поля CoCO₃ при повышении S_СО2 до 10^-1,5.

Фиг. 7.30в отражает типичные случаи образования поля сульфидов при добавлении к системе серы. С помощью этой диаграммы мы устанавливаем взаимоотношения карбоната, гидроокислов и сульфида кобальта в карбонатизированных и содержащих серу водах. Если сравнить положение полей сульфидов в рассмотренных выше диаграммах, то можно увидеть, что образование заметных концентраций металлических ионов и сульфатов происходит при примерно одинаковом окислительном потенциале. Такая особенность обусловливается довольно резким расхождением в значениях Eh между двухвалентной и шестивалентной серой. Данная особенность проявляется столь резко, что различия в устойчивости отдельных сульфидов в значительной степени затушевываются.

Диаграммы для кобальта составлены в 1957 г. Айвеном Барнсом, сотрудником геологического отделения Гарвардского университета.

ФИГ. 7.31а -7.31б

Соотношения между окислами вольфрама и его сульфидом. На диаграмме резко амфотерные свойства вольфрама отчетливо проявляются в больших размерах поля преобладания иона WO^2-₄ и в устойчивости WO₃ в кислых растворах. В природных условиях не показанные здесь катионы стремятся связать ион WO^2-₄ с образованием нерастворимых соединений типа CaWO₄ или FeWO₄. Сульфид вольфрама относительно устойчив, но и его поле в присутствии различных катионов замещается нерастворимыми вольфраматами. Следует заметить, что в условиях, которые здесь рассмотрены, WO₂ неустойчив в воде и что не следует ожидать присутствия в качестве устойчивой фазы металлического вольфрама, каким бы ни было его сопротивление коррозии.

Эти диаграммы рассчитаны в 1958 г. Кэртом Линном, сотрудником геологического отделения Гарвардского университета.

ФИГ. 7.32а -7.32в

Некоторые соотношения между соединениями урана и его ионами при 25°С и 1 атм общего давления.

С помощью фиг. 7.32а и 7.32б можно сравнивать влияние CO₂ на растворимость урана в системе открытой и закрытой по отношению к СО₂ (при постоянном значении SCO₂). В обоих случаях шестивалентный уран почти полностью комплексируется с образованием уранилдикарбонатных и ура-нилтрикарбонатных ионных компонентов, в связи с чем при заметных Р_CO2, или SCO₂ вытесняется поле устойчивости гидрата окиси уранила (скупита?). Такое комплексообразование протекает настолько эффективно, что при относительно высоких значениях Р_CO2 и S_CO2 поля указанных комплексов вытесняют поле устойчивости UO₂ (уранинита). Отсюда ясно, что карбонатсодер-жащие воды представляют собой прекрасные растворители урана.

Фиг. 7.32в служит иллюстрацией пока еще слабо разработанной но вероятно, весьма перспективной методики. Основная проблема, возникающая

1 (стр.210) Диаграмма для Со отличается от диаграммы для Ni существованием поля Со2O3, ниже линии разложения воды (в природе минералы стениерит, гетерогенит).- Прим. ред.

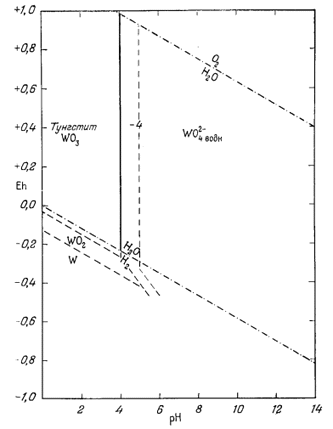Фиг. 7.31а. Соотношения устойчивости между некоторыми соединенниями вольфрама в воде при 25°С и 1 атм общего давления. Границы полей твердых веществ проведены при активности растворенных компонентов, равной 10-6; тонкая штриховая линия - изолиния акивности ионов, равной 10-4 по (Линну).

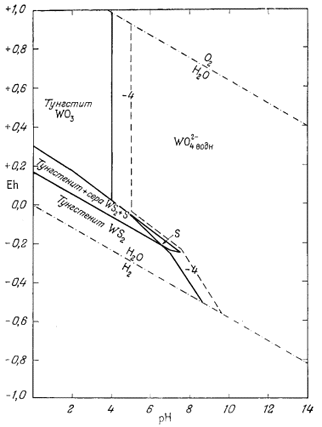Фиг. 7.31б. Соотношения устойчивости между некоторыми соединенниями вольфрама в воде при 25°С и 1 атм общего давления. Сумма растворенной серы равна 10-1. Границы полей твердых веществ проведены при активности растворенных компонентов, равной 10-6; тонкая штриховая линия - изолиния акивности, равной 10-4 по (Линну).

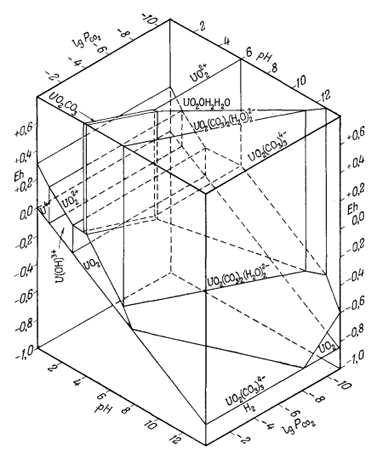Фиг. 7.32а. Соотношения устойчивости между некоторыми соединенниями урана в воде при 25°С и 1 атм общего давления как функция pH, Eh и PCO2. Границы полей твердых веществ проведены при суммарной активности урансодержащих компонентов, равной 10-6 (по Гаррелсу, Хостетлеру, Уиксу и Крайсту).

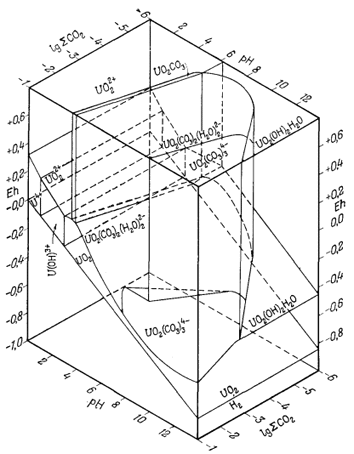Фиг. 7.32б. Соотношения устойчивости между некоторыми соединенниями урана в воде при 25°С и 1 атм общего давления как функция pH, Eh и суммы растворенных карбонатных компонентов. Границы полей твердых веществ проведены при активности суммы растворенных урансодержащих компонентов, равной 10-6 (по Гаррелсу, Хостетлеру, Уиксу и Крайсту).

при геологическом изучении окисленных урановых руд, - расшифровка условий миграции и осаждения урана. Как следует из фиг. 7.32а и 7.32б, при карбонатизации воды исключается осаждение гидрата окиси уранила. Вместе с тем известно, что в зоне окисления карнотит (уранилванадат калия) устойчив. На фиг. 7.32в представлено сечение многокомпонентной системы

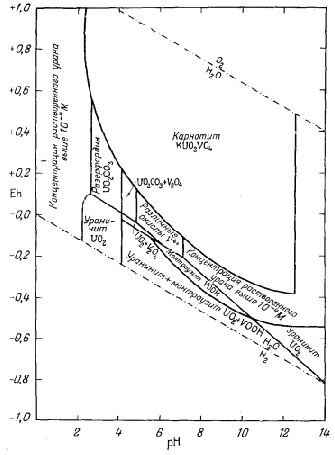Фиг. 7.32в. Соотношения устойчивости меякду некоторыми соединениями урана и ванадия в воде при 25° С и 1 атм общего давления. Сумма растворенных компонентов ванадия равна 10-3; сумма растворенных карбонатных компонентов равна 10-1; сумма растворенных калиевых компонентов равна 10-3 (по Гаррелсу, Хостетлеру Уиксу и Крайсту).

U - О₂ - Н₂О - К - V - СО₂, составленное для постоянных активностей К, V и CO₂ (т. е. соотношения "растворимости" урана относятся только к этой частной серии условий). Выбранные значения SК, SV и SCO₂ отвечают составу вод, характерных для зоны окисления уранованадиевых руд. Хотя, как правило, поля устойчивости твердых веществ следует изучать в широком диапазоне таких значений, но даже одно-единственное сечение может помочь нам выявить массу интересных закономерностей. "Валовая растворимость" урана в щелочной восстановительной среде определяется уранокарбонатными комплексными ионами, но и в этом случае имеется значительное поло карнотита. Расширению поля карнотита способствовало бы увеличение концентрации V или К в растворе, а повышение активности СО₂ сужало бы его размеры.

Все эти диаграммы составлены Хостетлером и Гаррелсом в сотрудничестве с Крайстом и Уиксом.

ФИГ. 7.33а -7.33б

Эти фигуры показывают, что диаграммы Eh - рН можно использовать при изучении влияния комплексообразования на растворимость металлов. В 1957 г. Джон Филлипс пытался отразить с помощью диаграмм Eh - рН роль сульфидных и хлоридных комплексов золота. Многие из соотношений, которые ему удалось получить, основаны на исследовании Краускопфа по растворимости золота [3, стр. 858-870]. Приведенные здесь диаграммы характеризуют активность ионов при низком и высоком содержаниях хлора и серы в системе. Диаграммы включают и соотношения, выведенные для очень широких пределов Eh, в том числе и значительно превышающих границы устойчивости воды, хотя реакции вне пределов устойчивости воды и не представляют для нас особого интереса. На самом деле диаграмма Eh - рН для золота несложна: в ней имеется лишь одно поле самородного золота, для которого активность ионов не превышает 10^-6. В присутствии больших количеств хлора золото немного растворяется в кислом окислительном растворе, переходя в ион AuCl^-₄. При высоком содержании серы в раствор переходит только очень небольшая часть золота в виде комплекса AuS^-, что характерно для широкого диапазона сильно восстановительных условий^{1 (стр.214)}. Обе закономерности представляют значительный геологический интерес. Во-первых, они свидетельствуют о возможности миграции золота в процессе окисления сульфидных руд, а во-вторых, могут помочь в решении проблемы переноса золота рудообразующими флюидами.

ВЫВОДЫ ПО РАЗДЕЛУ, ПОСВЯЩЕННОМУ ВОЗМОЖНОСТИ
ИСПОЛЬЗОВАНИЯ ДИАГРАММ Eh - рН

Выше уже указывалось, что при использовании диаграмм Eh - рН необходимо соблюдать определенные предосторожности. Ниже мы попытаемся рассмотреть различные стороны этой проблемы и покажем, какого рода выводы на основании этих диаграмм можно делать с уверенностью, а в каких случаях неосторожного исследователя подстерегают серьезные опасности. Не вызывает сомнений, что наилучшей гарантией в этом отношении служит доскональное изучение химии растворов. Здесь невозможно осветить все или даже небольшую часть тех вопросов, которые могут возникнуть, но все-таки мы укажем на основные достоинства и недостатки диаграмм Eh - рН.

ДАННЫЕ ПО СВОБОДНОЙ ЭНЕРГИИ

К сожалению, точность данных по стандартной свободной энергии образования, на которых основаны все рассмотренные диаграммы, весьма неравноценна, причем нам неизвестен удовлетворительный способ их проверки. С некоторой долей цинизма можно сказать, что величины, приведенные в приложении 2, редко столь же достоверны, сколь и важны. Вероятно, если в приведенных значениях отбросить один знак, они будут ближе к истинным. Большая часть наших сомнений связана с трудностью определения истинной природы перечисленных в таблицах веществ. Известно, что многие твердые вещества находятся в нескольких полиморфных модификациях, но далеко не все исследователи работали с той степенью тщательности, которая необходима для точного выяснения кристаллического состояния изученных ими веществ. Так, например, в экспериментах по определению свободной энергии твердых веществ методом осаждения не всегда было выдержано время, необ-

1 (стр.214) На диаграмме не показана область существования анионов AuS-2 и AuS3-3.- Прим. ред.

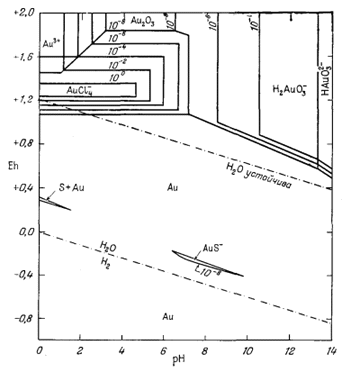Фиг. 7.33а. Соотношения устойчивости между некоторыми соединениями золота в воде при 25° С и 1 атм общего давления. Сумма растворенных хлоридных компонентов равна 10-3; сумма растворенной серы равна 10-6 (по Филлипсу).

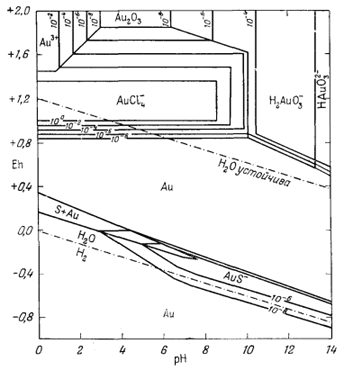Ф и г. 7.33б. Соотношения устойчивости между некоторыми соединениями золота в воде при 25° С и 1 атм общего давления. Сумма растворенных хлоридных компонентов равна 100; сумма растворенной серы равна 10-1 (по Филлипсу).

ходимое для полного старения осадка, или же осадок получался недостаточно крупнокристаллическим. Кроме того, величины свободных энергий вообще можно получать с помощью самых разнообразных экспериментальных и расчетных методов, но использовать эти данные без критического подхода весьма опасно.

Однако отмеченные недостатки сказываются не только при построении диаграмм Eh - рН, но присущи любым термохимическим расчетам. Наилучшим руководящим принципом здесь, вероятно, должен служить здравый смысл: если, согласно расчетам, окажется, что фаза А устойчива по отношению к фазе В вследствие небольшой разницы в величинах свободных энергий, то фазу В следует исключить из рассмотрения, разумеется, с соответствующими оговорками. Особенно это касается косвенных методов расчета, при которых приходится иметь дело с разницей между относительно большими значениями свободной энергии образования.

Имеющиеся величины DF°_обр относятся в основном к твердым веществам, состав которых наиболее близок к теоретическому. Минералы же по отношению к этим стандартам представляют собой "нечистые" соединения. Таким образом, диаграмму, иллюстрирующую соотношения между "чистыми" химическими соединениями, не следует целиком переносить на соотношения между реальными минералами. Вообще говоря, расхождение в величинах свободной энергии образования, обусловленное примесью посторонних элементов в структуре данного химического вещества, невелико (обычно оно почти пропорционально содержанию примеси). Наиболее серьезные ошибки, вероятно, допускает тот исследователь, который забывает о том, насколько сильно отличается состав минерала от состава чистых конечных продуктов, или о том, в какой степени отличается структура обычных минералов от структуры соответствующих химических соединений. Например, некоторые природные соединения типа доломита характеризуются переменным составом; однако, в какой степени это сказывается на их устойчивости, нам пока неизвестно. Некоторые сфалериты, для удобства расчетов принимаемые за соединение состава ZnS, на самом деле могут содержать от 10 до 14% железа.

Продолжая наши рассуждения в том же духе, мы как геологи оказываемся в затруднительном положении при попытке построить диаграмму, которая отражала бы условия отложения минералов железа, выпадающих в осадок в результате химических реакций. Следует ли рассчитывать соотношения устойчивости для кристаллических веществ - гематита и гётита - или же природная система контролировалась свежеосаждавшимся и значительно менее устойчивым гидроокислом с переменным содержанием воды? Этот вопрос еще раз пробуждает наши сомнения в том, насколько правомочно. при характеристике природных ассоциаций использовать данные, полученные для химических соединений.

ВЛИЯНИЕ ТЕМПЕРАТУРЫ И ДАВЛЕНИЯ

Все наши расчеты справедливы для условий 25°С и 1 атм общего давления. Однако возможность их применения совершенно ясна, поскольку эти условия весьма незначительно отличаются от природных, свойственных поверхностным и близповерхностным средам. Попытаемся выяснить, какой же именно порядок ошибки мы можем ожидать при исследовании, например, системы, находящейся под давлением нескольких атмосфер и при температуре 15 или 35° С?

Вопросу о влиянии изменения температуры и давления на минеральные равновесия будет посвящена гл. 9. Здесь же мы приведем лишь некоторые результаты.

В качестве примера рассмотрим зависимость соотношения между магнетитом и гематитом от Eh и рН:

2Fе3O4 крист + Н2Ожидк = 3Fе2О3 крист + 2H+водн + 2е

При 25° С этой реакции соответствует уравнение

Eh = 0,221 - 0,059 рН.

То же уравнение при 35° С примет следующий вид:

Eh = 0,227 - 0,061рН.

Такое расхождение можно свободно отобразить на диаграмме. Порядок величин в рассмотренном случае характерен для интересующих нас реакций; число соотношений, для которых влияние температуры сказывается резче, весьма невелико, но все же они существуют. Некоторые диаграммы рассчитывались и для 110° С, причем оказалось, что, хотя положение полей устойчивости относительно осей координат в этих случаях изменялось, размеры и форма этих полей оставались прежними. В общем изменение температуры на несколько градусов не влечет за собой искажения диаграммы, ибо границы между фазами смещаются не более чем на ширину линии.

Теперь обратимся к реакции

3Feкрист + 4Н2Ожидк = Fe3O4 крист + 4Н2 газ

и рассмотрим ее при 25°С. При условии равновесия

DF°реакции = DF°обр Fe3O4 + 4DF°обр H2 - 3DF°обр Fe - 4DF°обр H2O,
DF°реакции = -242,6 + 4.(0) - 3.(0) - 4.(-56,69),
DF°реакции = -15,6 ккал.

Отсюда

-15,6 = -1,364 lg K = -1,364 lg f4H2,
fН2 = 102,85атм, fН2 = 708 атм.

Таким образом, фугитивность водорода в условиях равновесия при 25° С равна 708 атм. Столь огромное значение фугитивности не может быть приравнено к парциальному давлению. Действительно, по фиг. 2.3 мы находим, что соответствующее равновесное давление равно приблизительно 500 атм. В нашем расчете мы пренебрегли лишь влиянием повышения давления на активность твердых веществ и жидкую воду. Поскольку изменения в величинах активности взаимоисключают друг друга, то подобные поправки будут незначительны.

Итак, при построении диаграмм устойчивости увеличением общего давления до нескольких десятков атмосфер можно безболезненно пренебрегать, если парциальные давления участвующих в реакции газов невелики. Вместе с тем при больших значениях фугитивности, равновесной для данной реакции, ее следует специально рассчитывать. Соответствующие равновесные парциальные давления связаны с фугитивностью коэффициентом активности газа [уравнение (2.4)].

ДИАГРАММЫ СПРАВЕДЛИВЫ ТОЛЬКО ДЛЯ
РАССМОТРЕННЫХ КОМПОНЕНТОВ

Пользуясь диаграммами Eh - рН, следует помнить, что с помощью термохимических расчетов можно получить ответы только на вполне конкретные вопросы. Например, можно рассчитать, что FeO и Fе₃O₄ при каких-то значениях Eh и рН находятся в равновесии, но если на основании этого расчета мы примем, что ассоциация FeO и Fe₃O₄. устойчива в системе железо - вода - кислород, то допустим грубую ошибку. Данный расчет не касается всех соотношений в системе. Если же рассмотреть все возможные реакции, то окажется, что FеО_крист будет необратимо переходить в другие равновесные соединения:

4FеО_крист = Fe₃O_{4 крист} + Fе_крист; DF_{реакции} отрицательна.

Затруднения такого рода геологу обычно не страшны. Он знает минеральные парагенезисы, характерные для определенного месторождения, и может ставить конкретные вопросы относительно условий, в которых возможно устойчивое сосуществование этих минералов. Очень ценны даже отрицательные ответы, например вывод, согласно которому фазы А и В не могут сосуществовать в равновесии. Итак, вычисления дают положительные или отрицательные ответы: фазы А и В могут существовать в равновесии друг с другом в данной системе, если ни одна из них не является неустойчивой по отношению к некоторому третьему компоненту или если А и В не взаимодействуют; в противном случае равновесное сосуществование фаз А и В невозможно.

ПЕРЕХОД ОТ АКТИВНОСТИ К РАСТВОРИМОСТИ

Вычисление активностей растворенных компонентов, находящихся в равновесии с твердыми веществами, чревато опасностями в той же степени, что и вычисление полей устойчивости твердых веществ. Вероятно, существует какой-то коварный недуг, который заставляет исследователя определять растворимости по активностям. Как указывалось в гл. 2, активность иона отличается от его моляльности на коэффициент g; этот коэффициент иногда можно довольно точно определить, пользуясь понятием ионной силы. Чтобы рассчитать растворимость твердого вещества при данных Eh и рН, следует знать активности всех растворенных компонентов, определяющих величину растворимости, а также их коэффициенты активности. Пренебрежение каким-либо присутствующим ионом или ошибка в определении коэффициента активности приводит к ошибке в вычислении растворимости. На этот момент обращалось внимание в гл. 2.

С геологической точки зрения более серьезное затруднение обусловлено противоположной ситуацией: даны состав природной воды, ее Eh и рН, известны минералы, с которыми соприкасается эта вода. Можно ли установить, что эти минералы находятся в равновесии с окружающей их средой? Если устойчивость можно выразить в виде функции только Eh и рН (как, например, в случае Fe₂O₃), то трудности снимаются, так как обе эти переменные определяют собой и активности. Однако если нужно определить активность иона кальция в равновесии с кальцитом, то мы возвращаемся к проблеме расчета активности данного иона по данным анализа, характеризующего сумму растворенного элемента. Решение такого вопроса, конечно, обратно расчету растворимости.

Несмотря на указанные затруднения, мы вправе сделать следующее важное обобщение: если данное вещество находится в равновесии с раствором, то сумма активностей всех известных растворенных компонентов, содержащих данный элемент, почти всегда меньше концентрации этого же элемента, определяемой химическим анализом.

Следовательно, можно производить вычисления суммы активностей ионов в равновесии с твердым веществом, - считая, что эта сумма отвечает величине минимальной растворимости. Вновь мы сталкиваемся с положительным или неопределенным ответом: если сумма активностей известных ионов велика, то можно сказать о данном твердом веществе, что оно растворимо; если же сумма активностей известных ионов незначительна, то твердое вещество может и не быть растворимым.

Кстати, следует подчеркнуть, что мы располагаем пока очень скудными данными относительно соотношений между породообразующими минералами и химическим составом связанных с ними водных растворов. Будь у нас эти данные, мы могли бы сделать немалые успехи. Допуская существование равновесия между минералами и раствором, каждый из нас может рассчитать растворимость данного элемента. Расхождение между полученным значением растворимости и аналитической концентрацией данного элемента в растворе будет отражать степень нашей некомпетентности. Тогда можно попытаться выяснить, обусловлено ли такое расхождение отклонением от равновесия, наличием неучтенных комплексов, неточными термохимическими данными или же какими-либо прочими факторами.

УПРАЖНЕНИЯ

7.1. а. Напишите реакцию для случая равновесия между SnО_крист и SnO_{2 крист}, выразив ее через воду, водородные ионы и электроны.
б. Рассчитайте изменение стандартной свободной энергии этой реакции при 25° С.
Ответ: DF°_{реакции} = - 5,0 ккал.
в. Рассчитайте Е° для той же реакции при 25° С.
Ответ: Е° = - 0,108 в.
г. Составьте уравнение, определяющее границу между фазами SnО_крист и SnO_{2 крист}, в единицах Eh и рН.
Ответ: Eh = - 0,108 - 0,0592 рН.
д. Какова активность Sn⁴⁺ в равновесии с SnO_{2 крист} при рН = 8?
Ответ: [Sn⁴⁺] = 10-39,7.
е. Какова активность Sn²⁺ в равновесии с SnО_{2 крист} при рН = 8 и Eh = = 0,3 в?
Ответ: [Sn²⁺] = 10-44,8.
7.2. Постройте диаграмму, иллюстрирующую устойчивость SnO_крист и SnО_{2 крист} в зависимости от Eh и рН при 25° С. Проведите изолинии активностей Sn⁴⁺_водн, Sn²⁺_водн и НSnО^-2 водн, равных 10^-6. Какой вывод можно сделать относительно устойчивости SnО_крист в воде? Устойчиво ли SnO_крист по отношению к Sn(ОН)_{2 крист}?
Ответ: SnO_крист взаимодействует с водой с освобождением водорода. Да, SnО_крист устойчиво по отношению к Sn(ОН)_{2 крист}.

Л И Т Е Р А Т У Р А

1. C l a r k W. M., C o h e n В. An analysis of the theoretical relations between reduction potentials and рН, Public Health Reports, Reprint 826, 1923.
2. G a r r е 1 s R. M., H о s t e t 1 e r C. L. С h r i s t., W о о k s A. D. Stability of uranium, vanadium, copper, and molybdenum minerals in natural waters at low temperatures and pressures, Paper delivered at meeting of Geological Society of America, Atlantic City, November, 1957.
3. К r a u s k о p f K. В. The solubility of gold, Econ. GeoL, 46, 858-870, 1951.
4. M a s о n В. Oxidation and reduction in geochemistry, Journ. GeoL, 57, 62-72, 1949. (Есть русский перевод: М е й с о н Б. Окисление и восстановление в геохимии, в сб. "Вопросы физике-химии в минералогии и петрографии", M., ИЛ, 1950.)
5. P o u r b a i x M. J .N. Thermodynamics of Dulite Aqueous Solutions, London, Edwar Arnold and Co., 136 pp., 1949.
6. S t a r k e у R. L., W i g h t K. M. Anaerobic Corrosion of Iron in Soil, New York, American Gas Association, 108 pp., 1945.
7.V a l e n s y G. Contribution au diagramme potential-pH du soufre, Compt. rend. 2eme Reunion, Cornito intern, thermo. kinetics electrochim., Milan, 51-68, 1950.
8. Z о В e 1 1 C.E. Studies on redox potentials of marine sediments. Bull. Am. Assoc. Petrol. Geol., 30, 477-513, 1946.
9. Щ е р б и н а В. В. Окислительно-восстановительные потенциалы в применении к изучению парагенезиса минералов, Докл. АН СССР, 22, № 8, 508-511, 1939.

РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА

Р о u г b a i x M. J. N., V a n M u y l d e r J., d e Z h o u b o v N. Atlas d'Equilibres Electrochimiques a 25°C, Paris, Gauthier-Villars, 1963.
P o u r b a i x M. J. N. Thermodynamics of Dulite Solutions, London, E. Arnold, 1949. Technical Reports of the Belgian Center for Study of Corrosion, 24 Rue des Chevaliers, Brussels.
1. P o u r b a i x M. Sur I'interpretation thermodynamique de courbes de polarisation, 1952.
2. P o u r b a i x M. Applications de diagrammes tension-pH relatifs au fer et a 1'eau oxygenee. Experiences do demonstration, 1954.
3. D e l t o m b e E., P o u r b a i x M. Comportomcnt electrochimique du cadmium, 1953.
4. S c h m e t s J., P o u r ba i x M. Comportement electrochimique du titane, 1953.
5. D e l t o m b e E., P o u r b a i x M. Comportement electrochimique des cyanures, 1953.
6. D e l t o m b e E., P o u r b a i x M. Comportement electrochimique du cobalt, 1954.
7. D e l t o m b e E., P o u r b a i x M. Comportement electrochimique du fer, 1954.
8. D e l t o m b e E., P o u r b a i x M. Comportement electrochimique du fer en solution carbonique, 1954.
9. P о u r b a i x M. Sur la phosphation oxydante des aciers ordinaires, 1953.
10. V a n M u y l d e r J. La corrosion et la protection des games en plomb des cables onterres, 1953.
11.V a n M u y l d e r J., P o u r b a i x M. Corrosion et protection catho-diquc du fer. Experience de demonstration, 1953.
12. V a n M u y l d e r J.Au sujet des hydrures de plomb et de la pulverisation cathodique du plomb, 1954.
13. V a n M u y l d er J., P o u r b a i x M. Sur le Comportement electrochimique du plomb. Corrosion, protection cathodique, passivation, 1953.
14. V a n M u y l d e r J., P o u r b a i x M. Corrosion et protection catho-diques du plomb, 1954.
15. M a g e e G. M. Corrosion electrolytique de 1'acier dans le beton (trad. d'un article de Magee G. M. paru dans Corrosion, 5, 11, 378-382, novem-ber 1949), 1954.
16. W a t t e c a m p s P. Progress recents de la technique americaine d'appli-cation des revetcments protecteurs, 1953.
17. Bureau of Ships, U. S. Navy (Trad. par Wattecamps P.), Etudes sur des systemes de revetements anticorrosif et antisalissant pour carenes de navires.
18. M o u s s a r d A. M., B r e n e t J., J o l a s P., P o u r b a i x M., V a n M u y l d e r J. Comportement electrochimique du manganese, 1954.
19. A b d E l W a h e d A. M., P o u r b a i x M. Utilisation des corbes de polarisation pour 1'etude des circonstances de corrosion et de protection du fer en presence de chlorures. Phosphatation et phosphatation oxydante, 1954.
20. P o u r b a i x M. Applications de 1'electrochimique a des etudes de corrosion, 1954.
21. P o u r b a i x M. Vue d'ensemble sur le Comportement electrochimique des metaux (lere partie), 1953.
22. Comptes-rendus des Journees d'Etudcs du Cebelcor, 13 et 14 avril, 1955.
23. D e l t o m b e E., d e Z o u b o v N., P o u r b a i x M. Comportement electrochimique du nickel, 1955.
24. L a u r e y s J.,V a n M u y l d e r J., P o a r b a i x M. Note sur 1'effi-cacite d'un appareil de traitement magnetique des eaux, 1955.
25. D e 1 t о m b e E., d e Z o u b o v N., P o u r b a i x M. Comportement electrochimique de 1'etain, 1955.
26. d e Z o u b o v N., D e l t o m b e E. Enthalpies libres de formation standard de 1'hydrure d'etain gazeux.
27. d e Z o u b o v N., D o l t o m b e E., P o u r b a i x M. Comportement electrochimique du germanium, 1955.
28. Enthalpies libres do formation standards, a 25°C, 1955.
29. D e l t o m b e E., d e Z o u b o v N., P о u r b a i x M. Comportement electrochimique du vanadium, 1956.
30. P o u r b a i x M. Lecons sur la corrosion electrochimique, 2me fascicule, 1956.
31. D e l t o m b e E., d e Z o u b o v N., P o u r b a i x M. Comportement electrochimique de 1'uranium, 1956.
32. D e l t o m b e E., d e Z o u b o v N., P o u r b a i x M. Comportement electrochimique du tungstene, 1956.
33. D e l t o m b e E., d e Z o u b o v N., P o u r b a i x M. Comportement electrochimique. du tellure, 1956.
34. V a n M u у 1 d e r J., P о u r b a i x M. Comportement des anodes reacti-ves en magnesium et en zinc, 1956.
35. D o l t o m b e E., d e Z o u b o v N., P o u r b a i x M. Comportement electrochimique du molybdene, 1956.
36. V a n E i j n s b e r g e n J.F.H. La protection contre la corrosion de 1'acior par des couches metalliques, specialement par la galvanisation a chaud, 1956.
37. V a n d e r v o l d e n F., P o u r b a i x M. Protection contre la corrosion dans 1'emballagc et au cours du stockage, 1956.
38. P o u r b a i x M. Services que peuvent rendre a 1'industrie petrolliere les centres de recherche contre la corrosion, 1956.
39. V a n M u y l d e r J., P o u r b a i x M. Comportement electrochimique du magnesium, 1956.
40. P о u r b a i x M. Sur la corrosion du fer et des aciers par les eaux. Influence du pH, des oxydants, des reducteurs, des chlorures, des phosphates et de la temperature, 1956.
41. D e l t o m be N., d e Z o u b o v N., P o u r b a i x M. Comportement electrochimique du chrome, 1956.
42. D e l t o m b e E., P o u r b a i x M. Comportement electrochimique de 1'aluminium, 1956.
43. P o u r b a i x M., d e Z o u b o v N. Sur les conditions des passivation du fer par les chromates, molybdatcs, tungstatcs et vanadates, 1957.
44. V a l e n s i G., D e l t o m b e E., d e Z o u b o v N., P o u r b a i x M. Comportement eloctrochimique du chlqre, 1957.
45.M a r a g h i n i M., V a n R y s s e l b e r g h e P., D e l t o m b e E., d e Z o u b o v N., P o u r b a i x M. Comportement electrochimique du zirconium, 1957.
46. V a n M u у 1 d e r J., P о u r b a i x M. Comportement electrochimique de 1'arsenic, 1957.
47. D e l t o m b e E., d e Z o u b o v N., P o u r b a i x M. Comportement electrochimique du bore, 1957.
48. Van Muylder J., Pourbaix M. Comportement electrochimique du bismuth, 1957.
49. P o u r b a i x M. Lecons sur la corrosion electrochiiniquu. 3me fascicule, 1957.
50. d e Z o u b o v N., P o u r b a i x M. Comportement electrochimique du technetium, 1957.
51. d e Z o u b o v N., P o u r b a i x M. Comportement electrochimique du rhenium, 1957.
52. V a n M u y l d e r J., P o u r b a i x M. Comportement electrochimique du tantale,- 1957.
53. V a n M u y l d e r J., d e Z o u b o v N., P o u r b a i x M. Comporte-mcnt electrochimique du niobium, 1957.
54. P i t m a n A. L., P o u r b a i x M., d e Z o u b o v N. Comportement electrochimique de 1'antimoine, 1957.
B 1 u m e r M. Die Existnnzgronzen anorganischer lonen bei der Bildung von Sedimentgesteinen, Helv. Chim. Acta, 33, fasc. VI, No. 206, 1950.
D e 1 a h а у Р., P o u r b a ix M., V a n R y s s e l b o r g h e P, Potential-pH diagrams, Journ. Chem. Educ., 27, 683-688, 1950.
C h a r i o t G. Theorie et methode nouvelle d'Analyse qualitative, 3rd od., Paris, Masson, 1949.
S c h m i t t H. H. (ed.). Equilibrium Diagrams for Minerals, Cambridge, Mass., Geological Club of Harvard University, 1962.
S i 1 1 e n L. G. Rcdox diagrams, Journ. Chem. Educ., 29, 600-608, 1952.

[Содержание] [Глава 6] [Глава 8]