| Р.М. Гаррелс, Ч.Л. Крайст | Растворы, минералы, равновесия |
|
|
|
|
[Содержание] [Глава 7] [Глава 9] |
|
|
|
|
Многие твердые вещества в контакте с водным раствором обнаруживают заметную тенденцию терять одни компоненты, сохраняя другие. При этом теряемые компоненты замещаются подобными компонентами из раствора, но в целом структура первоначального вещества не изменяется.
Если потерянные или приобретенные компоненты представляют собой ионы, процесс называется ионным обменом, его можно подразделить на катионный обмен и анионный обмен. Катионному обмену экспериментаторы уделяли гораздо больше внимания, чем анионному, поэтому и в настоящей книге будет описано почти исключительно первое из упомянутых явлений. Однако эти процессы по существу одинаковы, так что подробное рассмотрение катионного обмена позволит установить принципы, необходимые для такого же анализа анионного обмена.
Вещества, представляющие интерес для геолога и проявляющие заметную склонность к катионному обмену, обычно состоят из отрицательно заряженной повторяющейся структурной решетки. Последняя имеет совершенно определенные отрицательно заряженные места, занятые одно- или двухзарядными катионами. Классическим примером могут служить глинистые минералы, особенно монтмориллониты и иллиты (гидрослюды). В этом случае отрицательная решетка состоит в основном из листоватых структур алюмосиликата и способные к обмену катионы располагаются в межплоскостных положениях или примыкают к поверхностям частиц. Если частицы алюмосиликатов поместить в водный раствор, то часть межслоевых и поверхностных катионов может быть удалена и быстро замещена катионами иа раствора. Частицы минерала при этом регенерируются без существенных структурных нарушений.
Так же как и глинистые минералы, хотя, вероятно, не столь отчетливо, ведет себя большое число веществ, в общем характеризующихся прочной отрицательно заряженной решеткой, в которой рассеяны слабо заряженные катионы. К таким веществам относятся большинство силикатов, силикатные стекла, природные и синтетические арсенаты, ванадаты, молибдаты и родственные им соединения. Кроме того, сюда следует отнести обширный класс синтетических соединений, главным образом органических, которые при сохранении общей структурной целостности обладают обменными катионами с требуемыми характеристиками.
Хорошо известно значение воздействия катионного обмена на свойства и состав типичных природных растворов, протекающих через иониты. Но существует и другой аспект проблемы ионитов, который, возможно, столь же важен, но гораздо менее изучен. Если вещество с катионообменными свойствами помещается в качестве перегородки между двумя растворами разного состава, наблюдается тенденция к установлению равновесия между этими растворами путем миграции катионов через ионит. В этих условиях ионит ведет себя как полупроницаемая мембрана. Возникают электрические потенциалы, и два раствора со временем изменяют свой состав, причем характер изменения состава определяется свойствами ионообменной мембраны. В геологических условиях такая ситуация возникает всюду, где сланец залегает между двумя слоями песчаника, содержащими воды различного-состава.
Поведение ионитов как полупроницаемых мембран привело к их использованию в качестве чувствительных к катионам электродов, часть которых избирательна к определенным катионам. Хорошо известным примером такого-применения обменных мембран может служить стеклянный электрод для измерения активности иона водорода. В последнее время созданы стекла, избирательна чувствительные к катионам щелочных и щелочноземельных металлов. Они позволяют измерять, например, pNa = - lg[Na+] аналогично привычному измерению рН. Использование стеаратов и родственных им соединений позволило создать электроды, избирательные по отношению к катионам щелочных земель. В качестве электродов применяются и глинистые минералы, хотя они в общем не обладают высокой избирательной способностью по отношению к катионам щелочных металлов или щелочных земель при совместном нахождении катионов этих двух групп. С той же целью используются и синтетические обменные вещества.
Ниже будут рассмотрены
процессы катионного обмена с участием погруженных в раствор частиц, а
затем поведение ионитов, которые могут быть использованы как электроды,
если поместить их в качестве мембран между растворами разного состава.
Многие вещества, несомненно обладающие катионообменными свойствами, изучены довольно хорошо. Интересно, что их поведение относительно пары катионов почти всегда описывается достаточно простыми уравнениями. Если ионит с обменными местами, занятыми данным катионом, помещен в раствор другого катиона, происходит обмен. Отношение концентраций ионов в ионите можно определить как функцию активностей ионов в растворе при переменном составе раствора. Зависимость логарифма отношения активностей ионов в водном растворе от логарифма отношения концентраций ионов. в ионите имеет прямолинейный характер. На фиг. 8.1 показаны типичные зависимости логарифма отношения активностей одновалентных катионов в растворе от логарифма отношения их концентраций.
Уолтон [7] привел результаты целой серии экспериментов по изучению ионного обмена на различных ионитах. Он получил вид зависимости, иллюстрируемый фиг. 8.1. Эти соотношения могут быть описаны уравнением
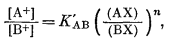 |
(8.1) |
где [А+] и [В+] - активности катионов в растворе, (АХ) и (ВХ) - концентрации ионов в ионите, n - показатель степени, а К'AB - константа обмена.
В табл. 8.1, заимствованной в сокращенном виде из работы Уолтона [7], приведены величины К' и n для различных веществ.
Активности ионов в растворе найдены по составу раствора и по коэффициентам активности, полученным методами, описанными в гл. 2. Концентрации ионов в ионите могут быть определены несколькими способами. Обычно характеристики ионита исследуются прежде всего путем помещения его в ряд растворов, содержащих высокие концентрации данного катиона, так что обменные места занимаются преимущественно одним катионом, например ионом натрия. Затем ионит помещают в воду и добавляют другой катион в форме растворимой соли, например КСl. Регистрируя количество Na+, переходящее в раствор при добавлении КСl, и в конце концов вытесняя весь Na+ из ионита добавлением КСl, получаем сведения об обменной емкости ионита и о величинах отношений концентраций ионов в ионите и растворе.
Таблица 8.1
| Ионит | n | К' | Ионит | N | K' |
| Синтетический алюмосиликат NH4 (плавленый) + Na+ |
1,50 | 0,22 | Синтетический алюмосиликат Na (гель) + Ва2+ |
1,82 | 3,2 |
| Синтетический алюмосиликат NH4 (плавленый) + К+ |
1,39 | 1,00 | Синтетический алюмосиликат NH4 (плавленый) + Са2+ |
3,84 | 0,81 |
| Синтетический алюмосиликат Ag (плавленый) + Li+ |
1,45 | 0,00065 | Синтетический алюмосиликат NH4 (плавленый) + Mg2+ |
5,88 | 0,0029 |
| Синтетический алюмосиликат Ag (плавленый) + К+ |
2,17 | 0,01 | Синтетический алюмосиликат Са (плавленый) + Na+ |
1,11 | 0,028 |
| Синтетический алюмосиликат Ag (плавленый) + Тl+ |
2,00 | 0,35 | Синтетический алюмосиликат Са (гель) + Na+ |
1,39 | 0,115 |
| Li-бентонит + NH+4 | 1,25 | 1,52 | Казеин в Са-форме + Ва2+ | 1,33 | 1,28 |
| К-бентонит + NH+4 | 0,91 | 0,54 | |||
| Синтетический алюмосиликат Na (гeль) + Са2+ |
1,58 | 0,55 |
Например, если 100-граммовый образец монтмориллонита обработать рядом растворов NaCl, после чего все обменные места будут заняты ионами натрия, а затем поместить его в ряд концентрированных растворов КСl, обнаружится, что ионы натрия появятся в умеренной концентрации в первом растворе и во все меньших и меньших концентрациях в последующих растворах КСl. Если количество освобождающегося Na+ становится аналитически неопределимым, предполагается что обменные места заняты К+ и что общее количество Na+, выведенное из ионита, соответствует емкости последнего по отношению к Na+. Поскольку обмен происходит в водных растворах, Н+ является постоянным претендентом на обменные места. Обычно принято определять обменную емкость как емкость, наблюдающуюся при рН 7. В общем доля отрицательно заряженных мест, занятых Н+, невелика для растворов с рН 7 или выше, однако в некоторых системах может встретиться серьезная помеха со стороны Н+. Для большинства ионитов удобными единицами измерения обменной емкости являются миллиэквиваленты обменного катиона на 100 г ионита. В табл. 8.2 приведена обменная емкость некоторых обычных глинистых минералов, определенная описанным способом.
Использование эквивалентов обменных катионов вместо молей удобно потому, что каждый ионит имеет определенное число отрицательно заряженных мест, которое обычно может быть занято лишь определенным числом положительных ионов. Например, в идеальном случае для полного замещения натрия в каком-либо образце ионита необходимо лишь половинное количество молей кальция. В целом это соотношение выдерживается довольно хорошо,
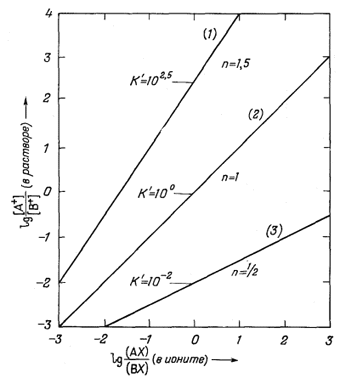 |
| Ф и г. 8.1. Зависимость между отношениями активностей ионов в
растворе и отношениями их концентраций в ионите для некоторых
ионообменников. Из уравнения (8.1) получаем lg([A+]/[B+]) = lg К'AB + n lg ([AX]/[BX]); как показано в тексте, зависимость между lg ([А+]/[В+]) и lg [(AX)/(BX)] изображается прямой линией, наклон которой равен n, a lg K'AB - отрезок, отсекаемый прямой на оси ординат. Приведены примеры для К' = 102,5, n = 1,5; К' = 100, n = 1; К' = 10-2, n = 0,5. |
но здесь проявляется одно из связанных с ионитами осложнений, заключающееся в том, что обменная емкость ионита, представляющаяся в идеальном случае как фиксированное число отрицательных мест, фактически различна для разных катионов.
Вследствие больших вариаций обменной емкости различных ионитов, или ионообменных субстратов, во многих отношениях удобнее использовать долю полной обменной емкости, занятую данным катионом, а не его абсолютную концентрацию. Для этой цели наиболее пригодной количественной мерой, по-видимому, является мольная доля данного иона в субстрате. Если полная обменная емкость монтмориллонита составляет 10 мэкв для 10-граммового образца, а количества ионов Na+ и К+ составляют соответственно по 5 мэкв, то число молей каждого равно 0,005. Мольная доля Na+ равна
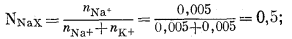 |
такова же и мольная доля К+ (NKX).
Таблица 8.2
| Минерал | Структурный контроль | Обменная емкость, мэкв/100 г при рН 7 | |
| Каолинит | Ненасыщенные валентности на краях структурных единиц |
3-15 | |
| Галлуазит (2Н2О) | То же | 5-10 | |
| Галлуазит (4Н2О) | Ненасыщенные валентности на краях структурных единиц и на внутренней поверхности между слоями |
40-50 | |
| Группа монтмориллонита |
Замещения в октаэдрических и тетраэдрических единицах, приводящие к возникновению избыточного отрицательного заряда; ненасыщенные валентности на краях структурных единиц |
70-1001 (стр.226) | |
| "Иллиты" (гидрослюды) |
Как в монтмориллоните, плюс недостаток К+ между слоями |
10-40 | |
| Вермикулит | Замещение межплоскостных катионов, подстановка внутри структурных единиц и ненасыщенные валентности на краях единиц |
100-150 | |
| Хлорит | Данные отсутствуют. Возможный недостаток заряда вследствие замещения в бруситовом слое |
10-40? | |
| Глауконит | Как в "иллитах" | 11-20+ | |
| Группа палыгорскита | Подстановка Al3+ вместо Si4+ в
структурных единицах; ненасыщенные обменные места внутри каналов в структуре |
20-30 | |
| Аллофан | Пористая аморфная структура с ненасыщенными валентностями |
~70 | |
| |||
Все существующие
интерпретации явлений катионного обмена в той или иной степени расходятся
с экспериментальными результатами. С этим вопросом читатель может детально
ознакомиться в специальных обобщающих работах по ионному обмену, список
которых приведен в конце настоящей главы. В основу нашей интерпретации
положен закон действия масс, что согласуется с широким использованием
этого закона в данной книге в целом.
Если ионит со своими отрицательно заряженными местами, занятыми одновалентным катионом, помещается в раствор, содержащий только один и при этом иной одновалентный катион, происходит обмен, и эмпирические соотношения, как указывалось ранее, описываются уравнением
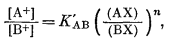 |
(8.1) |
где (АХ) и (ВХ) обозначают концентрации А+ и В+ в ионите в молях на единицу веса ионита. Эти концентрации могут быть также выражены в мольных долях. Если числитель и знаменатель уравнения (8.1) разделить на {(АХ) + (ВХ)}n, получим
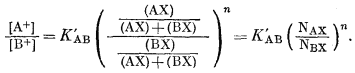 |
(8.2) |
Эмпирическое уравнение (8.1) можно вывести следующим образом, пользуясь законом действия масс. Реакция обмена такова:
| АХ + В+ = ВХ + А+ | (8.3) |
Предполагая наличие химического равновесия, имеем
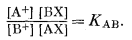 |
(8.4) |
После перегруппировки получим
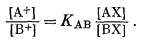 |
(8.5) |
Выражение (8.5) по форме подобно выражению (8.1) за исключением того, что в правой части уравнения вместо концентраций появляются активности и отсутствует показатель степени п. Если рассматривать ионит как бинарный твердый раствор с АХ и ВХ в качестве чистых компонентов, то, согласно уравнению (2.38), можно написать
| [АХ] = lAXNAX, | (8.6) |
| [BX] = lBXNBX, | (8.7) |
где lAX и lBX-рациональные коэффициенты активности. Подставляя (8.6) и (8.7) в (8.5), получим
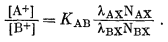 |
(8.8) |
Если ионообменный субстрат представляет собой регулярный раствор, то по уравнению (2.42)
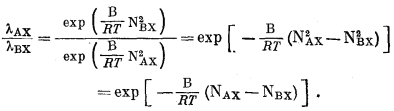 |
Подставляя это соотношение в уравнение (8.8), получим
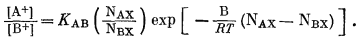 |
(8.9) |
Логарифмируем обе части уравнения:
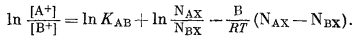 |
(8.10) |
Величина ln (NAX/NBX) может быть разложена в ряд
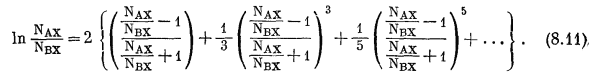 |
(8.11) |
Этот ряд быстро сходится для величин NAX и NBX, с которыми обычно имеют дело при экспериментальной работе на ионитах, т. е. для величин примерно между 0,1 и 0,9. В первом приближении ограничимся только первым членом ряда (8.11). Тогда
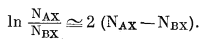 |
(8.12) |
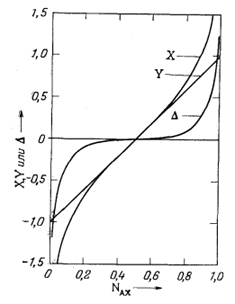 |
| Фиг. 8.2. График зависимости Х = 1/2 ln
(NAX/NBX), Y = (NAX -
NBX) и D = (X - Y) от
NAX. Обозначения те же, что и в уравнениях (8.10) и (8.13) в тексте, кроме Х и Y. Следует отметить, что D становится большим только тогда, когда величина NAX существенно отклоняется от 0,5. |
Подстановка этой величины в уравнение (8.10) дает
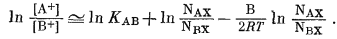 |
(8.13) |
Берем антилогарифмы обеих частей уравнения (8.13):
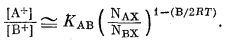 |
(8.14) |
Таким образом, уравнение (8.14) идентично эмпирическому уравнению обмена (8.2) с
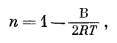 |
(8.15) |
и
| KAB = K'AB | (8.16) |
Приближение, с помощью которого было получено уравнение (8.12) из уравнения (8.11), дает очень хорошие результаты, если NAX @ NBX, и плохие лишь в том случае, если NAX намного больше или намного меньше NBX. Это заставляет предполагать, что эмпирическое соотношение Уолтона [уравнение (8.1)] является приближением, которое приемлемо только для величин NAX или NBX, значительно отличающихся от нуля или единицы, и что прямое применение теории регулярных растворов, выражаемое уравнением (8.9) (без использования приближенного ряда), может привести к более точным результатам. Различия, получающиеся при использовании уравнений (8.9) и (8.14), в виде некоторых функций отношения NAX и NBX показаны на фиг. 8.2.
Для одно-двухвалентного ионного обмена эмпирическое уравнение имеет следующий вид:
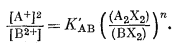 |
(8.17) |
Реакция этого обмена может быть написана следующим образом:
| A2X2 + B2+ = BX2 + 2A+, | (8.18) |
откуда
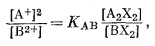 |
(8.19) |
или
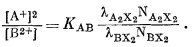 |
(8.20) |
Снова предполагая, что субстрат представляет собой регулярный раствор, и поступая так же, как при выводе уравнения (8.14) из уравнения (8.8), перейдем от (8.20), к уравнению
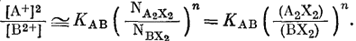 |
(8.20a) |
Обмену с участием более чем двух различных катионов посвящено, по-видимому, очень мало экспериментальных работ. Это довольно странно, поскольку в природных системах присутствует много различных катионов. Соотношения для трех одновалентных катионов могут быть выведены из закона действия масс на основе использованного выше допущения, касающегося отношения между активностью катиона в растворе и его концентрацией в ионите.
Для трех ионов А+, B+ и С+ можно написать следующие уравнения равновесия:
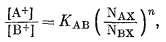 |
(8.21) |
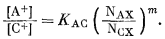 |
(8.22) |
Умножая уравнение (8.15) на уравнение (8.16), получим
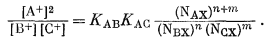 |
(8.23) |
Известно, что, если показатели степени n и
m равны каждый единице, уравнение (8.23), по крайней мере
приближенно, удовлетворяется.
Удивительно, что довольно простые уравнения, используемые при анализе реакций, происходящих в процессе катионного обмена, так хорошо описывают процесс. Ведь для этого должен быть соблюден ряд условий. Обменные места на отрицательно заряженной мембране должны вести себя почти идентично; катионы должны идти к мембране и от нее без заметного разрушения мембраны раствором или изменения ее структуры. Общее число доступных обменных мест должно оставаться практически постоянным. Активности катионов на отрицательной решетке должны быть связаны с их концентрациями экспонентными уравнениями идентичной формы.
Ни одно реальное вещество
не способно полностью удовлетворить всем этим требованиям. Некоторые
недостатки, вызывающие существенные отклонения от выведенных нами
уравнений, описываются ниже.
В веществах, состоящих из частиц неправильной формы и малого размера, поверхность частиц, кроме более или менее плоских граней, имеет большое количество ребер и вершин. Энергия, требующаяся для обмена катиона на вершине, заметно отличается от энергии, необходимой для обмена катиона на ребре, а для катиона на ребре - от энергии обмена катиона на поверхности. Ни одна константа обмена не может быть достаточной для описания реакции обмена в таком случае; наоборот, каждое небольшое приращение на кривой обменного титрования требует отдельной константы. Например, если ионы водорода находятся в обменных положениях и вытесняются ионами натрия, первое добавление ионов натрия освобождает ионы водорода довольно легко, но последующие добавки должны вытеснять ионы водорода из все более устойчивых положений.
Сходным образом ведут себя тонко растертые водные силикаты алюминия. Отрицательно заряженные места, имеющиеся на таких твердых веществах, появляются только при разрушении связей на поверхностях частиц и заметно различаются по своим свойствам вследствие влияния как геометрии поверхности, так и природы связей, разрушенных во время истирания.
Второй пример влияния неэквивалентных мест мы встречаем у глинистых минералов, когда они помещаются в кислый раствор и затем титруются
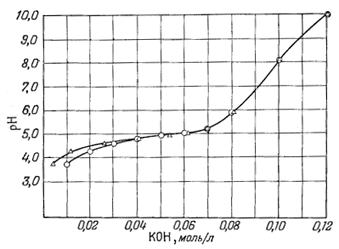 |
| Фиг. 8.3. Расчетная (треугольники) и экспериментальная (кружки)
кривые титрования для бейделлита из Путнема. Расчет основан на предположении, что две обменные реакции протекают по уравнениям 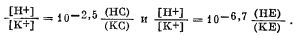 Заимствовано из работы Гаррелса и Крайста [4]. |
гидроокисью щелочного металла. Водородные глины ведут себя так, как будто в них имеются два отличающихся по положению водорода: один - легко вытесняемый катионами щелочного металла и другой - удерживаемый гораздо прочнее. Иллюстрирующая такое поведение кривая титрования приведена на фиг. 8.3. При допущении, что реакция обмена имеет вид
| НХ + К+ = КХ + Н+, |
константа обмена для первого положения будет равна
10-2,5, а для второго 10-6,7. В приведенном примере
обе константы хорошо выдерживаются во всем диапазоне их применения; на
этом основании можно полагать, что разница между энергиями связи
К+ и Н+ постоянна для каждого субстрата, но что эти
два субстрата неэквивалентны. Удовлетворительная физическая модель,
которая позволила бы объяснить наличие подобных двух отличающихся типов
отрицательных мест, пока не разработана.
Нужно всегда помнить, что
сама отрицательно заряженная решетка не остается инертной по отношению к
воздействию водного раствора, пока присоединяются и удаляются катионы.
Например, если магнезиальный монтмориллонит поместить в богатый натрием
раствор, так что, по существу, все его обменные места будут заняты
натрием, он не будет равновесным в отношении всех возможных химических
реакций. Некоторое количество магния, находящегося в восьмерной
координации, обычно переходит в раствор, а некоторое количество ионов
натрия входит в структуру решетки. Имеется мало данных о скорости, с
которой происходят такие изменения, но за какой-то период времени решетка
должна измениться. Более того, в ходе достижения полного равновесия все
компоненты отрицательной решетки должны частично перейти в окружающий
раствор. Это значит, что если вещество остается в воде, то должно
происходить некоторое растворение решетки, возможно сопровождающееся
перестройкой ее поверхности. Такой эффект лучше наблюдать при воздействии
кислых растворов на алюмосиликаты: в связи с высокой концентрацией
Н+ раствор обычно быстро разрушает их структуру, и погружение в
сильную кислоту, как правило, приводит к расхождениям между значениями
обменных емкостей, установленными до и после погружения. В некоторых
случаях в процессе воздействия раствора на структуру алюминий или другие
удаляемые из решетки ионы занимают обменные места, обычно занятые
катионами меньшей валентности.
Для пар одновалентных катионов константа обмена К' [уравнение (8.1)] служит наиболее удобной мерой избирательности ионита, т. е. его тенденции связывать один ион прочнее, чем другой. Например, если отношение активностей ионов А+ и В+ в растворе равно единице, когда их мольные доли в ионите равны, то ионит не обладает свойством избирательности: А+ и В+ связываются им с равной силой. Но если К'АВ равна 10, то равенство мольных долей ионов в ионите имеет место только в том случае, когда отношение активностей ионов в растворе равно 10. Наоборот, если отношение активностей ионов в растворе равно единице, ионит будет занят преимущественно одним из ионов.
Константы обмена, приведенные в табл. 8.1, показывают, что некоторые иониты обладают не очень высокой избирательностью. Силикатные стекла являются заметными исключениями из этого общего правила. Эти стекла подробно описаны в следующем разделе, посвященном мембранным электродам. Для некоторых из них наблюдались величины К' порядка 109.
Айзенман [2] разработал стройную теорию, объясняющую относительную прочность связей катионов в различных типах ионитов. Этот исследователь выводит изменение свободной энергии обмена (и тем самым константу обмена) для данного катионного обмена, исходя из рассмотрения энергии, необходимой для удаления катиона из его обменного места и перевода в гидратированное состояние в растворе, и изменения свободной энергии при одновременном перемещении другого катиона из раствора на обменное место. Расчеты энергий полностью основаны на учете кулоновских сил. Основываясь на анализе распределения зарядов в пределах ионита, Айзенман разработал концепцию "эквивалентного аниона". Суть ее в том, что каждый единичный отрицательный заряд на ионите рассматривается как связанный со сферическим атомом. Тогда, зная размер и заряд катиона, можно рассчитать энергию, требуемую для удаления катиона в вакуум на бесконечное расстояние. Аналогичным образом можно рассчитать изменение энергии при перемещении катиона из вакуума в гидратированное состояние в растворе, исходя при расчете, как и ранее, из размера и заряда катиона и размера и распределения заряда полярных молекул воды.
Основываясь на различных соотношениях размеров и зарядов катионов, размере "эквивалентного аниона" и энергиях гидратации катионов, можно предсказать существование 11 рядов энергий связи одновалентных катионов Na+, K+, Li+, Cs+ и Rb+. Как было установлено, эти ряды, а также порядок величины дифференциальных энергий связи согласуются с поведением реальных ионитов.
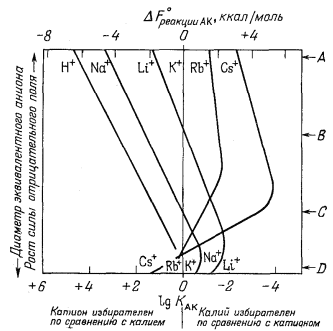 |
| Фиг. 8.4. Диаграмма, показывающая зависимость констант обмена
KАК Для различных одновалентных ионов А =
Н+, Na+ и т. п. по отношению к K+
от "диаметра эквивалентного аниона" Айзенмана. На оси ординат указаны реальные иониты: (A) Na - Аl-стекло (11,6% Na2O, 17,7% Al2O3); (В) Na-содалит; (С) Ag-пермутит; (D) глинистые минералы. По Айзенману [2]. |
Фиг. 8.4 (в упрощенном виде заимствованная у Айзенмана [2]) показывает зависимость относительных энергий связи от размеров эквивалентного аниона (от силы отрицательного электростатического поля). На оси ординат отмечено положение нескольких реальных ионитов. На оси абсцисс указаны дифференциальные энергии связи и константы обмена для катионов по отношению к калию. Например, натрий-алюминиевое стекло обладает отрицательным полем большой силы, или малым размером эквивалентного аниона. По силе связи с этим стеклом катионы располагаются в такой последовательности: H+ > Na+ > Li+ > K+ > Rb+ > Cs+. Дифференциальная энергия связи для Н+ по отношению к К+ равна примерно 6,7 ккал, т. е.
| КХ + Н+ = НХ + К+, | |
| DF°реакции = -6,7 ккал. |
Константа обмена (константа равновесия) для этой реакции (при 25° С) равна
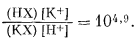 |
Следовательно, данное стекло высоко избирательно для Н+ по сравнению с K+, поскольку стекло было бы в равной мере занято Н+ и K+ только при отношении активности K+ и Н+, равном 104,9. К тому же данное стекло является отличным натриевым электродом. Хотя оно и предпочитает Н+ натрию, отношение Na+ к Н+ во многих растворах так высоко, что влияние Н+ ничтожно. Натрий является в высокой степени предпочтительным по сравнению со всеми остальными щелочными катионами.
Глинистые минералы обладают
полями малой силы, и эта особенность согласуется сих низкой
избирательностью. Кроме того, они попадают в участок многочисленных
пересечений кривых избирательной способности, что объясняет трудности,
встречавшиеся до сих пор при составлении для них рядов избирательности.
Недавно были разработаны электроды, избирательно чувствительные к некоторым катионам в природных водах. Эти электроды представляют собой типичные материалы, проявляющие свойства катионообменных субстратов в водном растворе. Если такие иониты поместить в качестве мембран между растворами различного состава, то путем измерения э. д. с. в растворе можно определить активность ионов в этом растворе. Следовательно, при измерении э. д. с. мы можем определить величины, непосредственно сравнимые с величинами, получаемыми с помощью расчетов на основе термодинамических данных. Это позволяет обойти затруднения, возникающие при попытке найти активности ионов по данным об общих концентрациях различных элементов, определяемых путем обычного химического анализа. Более того, будут быстро расширяться и наши знания о степени комплексирования ионов в природных водах, так как мы сможем сравнивать активности и концентрации.
Отбирая пробы вод,
находящихся в контакте с известными минеральными ассоциациями, и находя
активности путем электродных измерений, мы можем сравнивать их с
активностями, рассчитанными для случая равновесия с минералами, и, таким
образом, оценивать степень достижения равновесия.
Все чувствительные к катионам электроды действуют по одному и тому же принципу. Обменный субстрат можно представить себе как отрицательно заряженную жесткую пористую решетку, через которую обычно мигрируют
 |
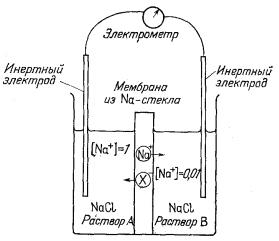 |
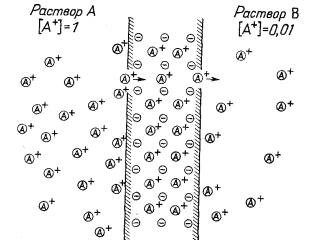
| Фиг. 8.5. Схематическая диаграмма с изображением отрицательно заряженной жесткой решетки и катионов, диффундирующих через мембрану под влиянием градиента активности. | Фиг. 8.6. Ячейка со стеклянной мембраной, иллюстрирующая возникновение потенциала между двумя разными растворами в результате перемещения катионов. |
катионы, но не могут двигаться анионы. Миграцию катиона в мембране, вероятно, следует рассматривать как процесс вытеснения, при котором вхождение одного катиона в ионит с одной стороны вызывает удаление какого-то катиона с другой стороны.
На фиг. 8.5 схематически показана катионообменная мембрана. Из-за большей активности А+ в растворе А существует тенденция переноса А+ в раствор В. Эту тенденцию можно оценить количественно с помощью соотношения для свободной энергии. Для процесса переноса катиона А+ из раствора, где его активность равна 1, в раствор, где активность А+ равна 0,01, пишем
| А+(а = 1) = А+(а = 0,01). |
На основании уравнения (1.13)
| DFреакции = DF°реакции + RT ln Q. |
Для рассматриваемого процесса DFреакции на 1 моль переносимого катиона равно
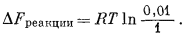 |
| A (a = 1) = A+ (a = 1). |
Изменение свободной энергии можно представить как электрический потенциал, который можно измерить на соответствующей экспериментальной установке. Такая экспериментальна система показана на фиг. 8.6, где стекло в натриевой форме выполняет функцию мембраны. Когда ионы натрия покинут раствор А, электроны будут удаляться из этого раствора через инертный электрод, поскольку должна быть сохранена электронейтральность раствора. Аналогично по мере поступления ионов натрия в раствор В электроны будут перемещаться в этот раствор, чтобы нейтрализовать избыток положительного заряда. Движение Na+ в ячейке слева направо через мембрану формально соответствует движению отрицательных мест в мембране справа налево. Таким образом, реакция в правой части ячейки соответствует диссоциации
| NaXB = Na+B (a = 0,01) + Х-B (правая часть ячейки), | (8.24) |
т. е. разобщению Na+ при активности 0,01 с отрицательными местами Х-, передвигающимися влево. В левой части ячейки избыток отрицательных мест соединяется с Na+ при активности 1, согласно реакции
| Na+A (a = l) + X-A = NaXA (левая часть ячейки). | (8.25) |
Эти две химические реакции совершенно аналогичны реакциям в полуячейках с освобождением и привнесем электронов и могут быть рассмотрены с помощью методов, описанных в гл. 1 для таких реакций в полуэлементах. Так, для окислительного потенциала, соответствующего уравнению (8.25), для 25° С пишем 1 (стр.234).
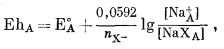 |
(8.26) |
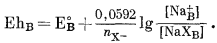 |
(8.27) |
Вычитая уравнение (8.27) из уравнения (8.26), получаем
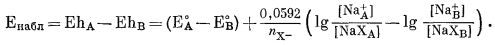 |
(8.28) |
Упрощая и принимая во внимание, что для этого процесса nX- = 1, получим
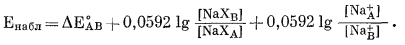 |
(8.29) |
Если две поверхности
мембраны ведут себя совершенно одинаково по отношению к растворам, мы
будем иметь DЕ°AB = 0 и
[NaXB]/[NaXA] = 1. Вообще говоря, при проверке это
не подтверждается, ибо, в действительности э. д. с. возникает и тогда,
когда по обе стороны мембраны находятся рас-
|
1 (стр.234) Чтобы написать уравнение (8.26) и последующие уравнения для любой температуры Т, заменяем множитель 0,0592 на (2,303 RT)/Б. |
творы с одинаковой активностью Na+. Однако для данной мембраны DЕ°AB и [NaXB]/[NaXA] постоянны в ходе измерения, так что уравнение (8.29) упрощается:
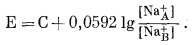 |
(8.30) |
В него входит эмпирический потенциал С, известный как потенциал асимметрии. Поддерживая постоянную активность Na+ в правой части ячейки (раствор В) и используя это для измерения неизвестной активности Na+ в растворе А, получаем наблюдаемую э. д. с.
| Е = С' + 0,0592 lg[Na+A], | (8.31) |
где С' = С - 0,0592 lg [Na+B]. Таким образом, э. д. с. ячейки изменяется на 0,0592 в при каждом десятикратном изменении [Na+] в растворе А.
Мембранные электроды хорошо работают лишь до тех пор, пока решетка остается "жесткой" и допускает движение только катионов. Если, например, отверстия в мембране достаточно велики для миграции отрицательных ионов как противотока миграции катионов, мембрана будет действовать как простой проводник, и э. д. с. между растворами станет малой даже при большой разнице активностей катионов. Если между растворами осуществляется свободный обмен катионами и анионами, величина остаточной э. д. с. фактически определяется только относительной легкостью миграции положительных и отрицательных ионов, зависящей от их чисел переноса. Такие остаточные потенциалы часто известны как потенциалы жидкостного соединения; величина их колеблется от нуля до примерно 100 мв.
Во всяком случае, изменение
э. д. с. на 0,0592 при десятикратном изменении активности катиона в
испытуемом растворе указывает на то, что мембрана допускает перемещение
практически одних только катионов.
Имеется много веществ, которые можно использовать как мембранные электроды. В настоящее время широко применяются силикаты, которые состоят из отрицательно заряженных повторяющихся структурных решеток высокой химической устойчивости с катионами, рассеянными по всей решетке.
Наиболее широким применением в качестве мембранных электродов пользуются силикатные стекла. Их преимущество заключается в относительно низком электрическом сопротивлении благодаря легкости, с которой катионы могут двигаться через рыхлую структуру стекла. Тем не менее удельное сопротивление таких стекол достаточно высоко, так что для измерений в цепях со стеклами в роли мембран необходимо разработать электрометры с высоким входным сопротивлением.
В производстве электродов использовались глинистые минералы с их слабо связанными межслоевыми катионами. Листоватые структуры алюмосиликатов работают как отрицательно заряженные мембранные решетки, а их межслоевые расстояния таковы, что позволяют мигрировать катионам, но препятствуют анионному противотоку.
В качестве электродов применялись также синтетические катеониты. Как и глинистые минералы, они состоят из инертного, отрицательно заряженного комплекса, на который не влияет прибавление или удаление катионов.
Полнокристаллические вещества, подобные трехмерным силикатам, с прочно связанными катионами, редко использовались как мембраны из-за направленности их свойств, в связи с чем возникали проблемы ориентировки мембраны. К тому же электроды из таких веществ имеют высокое удельное сопротивление вследствие относительной неподвижности их катионов. Поэтому проблема измерения потенциала все еще, по существу, не решена. Некоторые успехи достигнуты в результате растирания таких материалов и монтирования их в инертных субстратах. При надлежащем монтаже промежутки между поверхностями растертого материала (например, полевого шпата) и инертной среды (например, парафина) могут достичь как раз такой величины, чтобы допустить миграцию катионов способом вытеснения вдоль поверхностей частиц полевого шпата, но препятствовать анионным противотокам. Конструирование эффективных электродов подобного типа до сих пор в значительной степени определяется искусством экспериментатора. Измерения потенциалов для большинства таких электродов показывают, что часть. мембраны ведет себя идеально, т. е. допускает лишь миграцию катионов способом вытеснения, в то время как остальная часть электрода имеет отверстия, достаточно большие для почти свободного перемещения как катионов, так и анионов.
Интересно отметить, что
сравнительно недавно в качестве катионочувствительных мембран стали
использоваться тонкие пленки мыла, тщательно ориентированные путем
отложения серий мономолекулярных слоев. Есть. серьезные основания
надеяться, что они будут обладать высокой избирательностью к определенным
катионам. Подробнее о них будет сказано ниже.
В в е д е н и е. Сходство материалов, используемых в качестве ионитов и ионочувствительных электродов, свидетельствует о том, что ионообменные и электродные функции этих материалов - тесно связанные явления. Выше, при анализе поведения отрицательно заряженной мембраны с катионами, относительно свободно связанными с отрицательными местами, было высказано предположение, что поверхности мембраны заняты катионами такого же сорта, как и катионы, находящиеся внутри мембраны. Для большинства мембран найдено, что, если в испытуемом растворе присутствует несколько катионов, величины наблюдаемых э. д. с. являются функциями активностей более чем одного катиона. Другими словами, электрод измеряет изменение активности данного иона только в том случае, когда поверхность электрода, по существу, полностью занята этим ионом. Кроме того, для данного вещества именно ион, занимающий поверхность электрода, определяет э. д. с.; катионы внутри стеклянной мембраны просто передают заряд путем вытеснения друг друга.
Три варианта взаимоотношений, схематически представленные на фиг. 8.7, показывают, что электрод из натриевого стекла с внутренним стандартным раствором, имеющим постоянную активность Na+, может вести себя либо как Na+-элeктpoд, либо как К+-электрод, либо как электрод со смешанной Na+ - К+-функцией. Для большинства стекол наружные поверхности, подвергающиеся действию испытуемого раствора, редко занимаются единственным катионом и поэтому чувствительны более чем к одному катиону. Таким образом, с помощью многих имеющихся ныне мембранных электродов активность данного катиона может быть измерена лишь в том случае, когда электрод погружен в раствор, содержащий только этот катион. Если нужно, чтобы электрод был избирательно чувствителен к данному катиону в растворе, содержащем несколько катионов, этот катион должен быть связан с мембраной так сильно, чтобы все остальные катионы вытеснялись с ее поверхности.
Пока имеется мало электродов, достаточно избирательных для данного катиона, чтобы их можно было с надежностью использовать для измерения активности этого катиона при равной или больших активностях других катионов. Намного больше веществ можно использовать в качестве мембран, избирательных по отношению к двум или трем катионам и практически игнорирующих все другие катионы. Они могут применяться в том случае, если реакцию этого электрода в условиях, когда поверхность мембраны в испытуемом растворе частично занята каждым из этих избранных катионов, можно выразить в величинах э. д. с.
Э.д.с. д л я о д и н о ч н о г о к а т и о н а. Как было показано ранее, при выводе уравнений, связывающих электродные потенциалы с активностя-
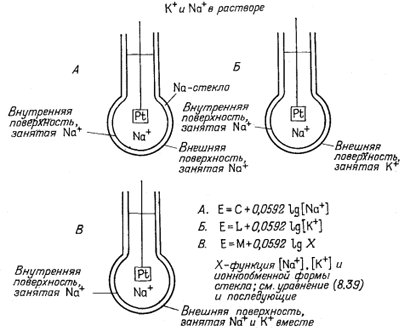 |
| Ф и г. 8.7. Три варианта применения электрода из натриевого
стекла. Электрод содержит внутри стандартный раствор с постоянной активностью Na+ и может действовать как Nа+-электрод (А), К+-электрод (Б) и влектрод со смешанной Na+- К+-функцией (В). Электрод погружен в раствор, содержащий и Na+ и К+, и свяэан с измерительной целью проводником, идущим от внутреннего Pt-электрода. |
ми катионов, удобно рассматривать мембранные электроды через соответствующие полуячейки. Электрод в виде шарика из натриевого стекла с раствором постоянной активности Na+ внутри шарика, подобный изображенному на фиг. 8.7, составляет полуячейку с постоянным потенциалом. По уравнению (8.26) для потенциала электрода
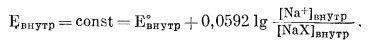 |
(8.32) |
Если электрод помещен в раствор, содержащий Na+ и внешняя поверхность занята только Na+, можно написать в соответствии с уравнением (8.27)
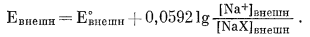 |
(8.33) |
Вычитая уравнение (8.32) из уравнения (8.33), получим
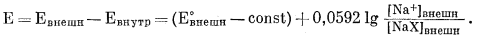 |
(8.34) |
Если внешняя поверхность занята только Na+, то активность NaX постоянна; [NaX]внешн является константой: обозначим ее через W. Тогда
| E = (E°внешн - const - lg W) + 0,0592 lg [Na+]внешн | (8.35) |
и
| Е = С' + 0,0592 lg [Na+]внешн, | (8.36) |
что совпадает с уравнением (8.31), выведенным ранее.
Если электрод помещен в испытуемый раствор, содержащий только К+, так что внешняя поверхность электрода занята одним К+, потенциал внутренней ячейки остается постоянным; потенциал внешней ячейки выразится через уравнение
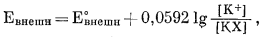 |
(8.37) |
где [КХ] постоянно. Комбинируя эти две полуячейки, как ранее, имеем
| Е = L' + 0,0592 lg[K+]. | (8.38) |
В этих условиях, когда внешняя поверхность электрода занята полностью одними ионами калия, электрод функционирует как К+-электрод. Константа L' отличается от константы для случая, когда электрод функционирует как Na+-электрод, но э. д. с. изменяется на 0,0592 в при каждом десятикратном изменении активности К+ во внешнем растворе.
Таким образом, мембранный электрод с внутренним раствором постоянного состава реагирует на катион во внешнем, или испытуемом, растворе,. занимающий всю поверхность электрода. Посредством градуировки электрода в растворе с известной активностью катиона изменение на 0,0592 в при десятикратном изменении активности катиона может быть использовано для определения активности катиона в неизвестных растворах.
Э.д.с. д л я д в у х о д н о в а л е н т н ы х к а т и о н о в. Используя уравнение (8.33), можно вывести соотношение для электрода, у которого поверхность занята двумя катионами. Если на поверхности электрода имеются и К+ и Na+, активность NaX или КХ не будет постоянной, и член [NaX] уравнения (8.33), например, не может входить в константу С' в уравнении (8.36). Наоборот, [NaX] будет колебаться от максимума, соответствующего полной занятости поверхности электрода ионами Na+, до нуля, соответствующего полной занятости поверхности ионами К+.
Исходя из уравнения (8.34), напишем для рассматриваемого случая
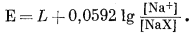 |
(8.39) |
Мы показали ранее, что если ионообменный субстрат, который в данном случае служит поверхностью электрода, подчиняется теории регулярных растворов, то, согласно уравнению (8.14),
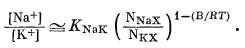 |
Заменив для удобства знак приблизительного равенства на знак равенства и обозначив
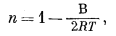 |
|
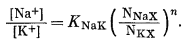 |
(8.40) |
Так как по закону действия масс,
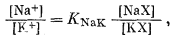 |
в силу уравнения (8.40)
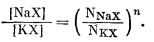 |
(8.41) |
Уравнение (8.41) можно переписать в виде пары сопряженных уравнений
| [NaX] = kNnNaX, | (8.42a) |
| [КХ] = kNnKX. | (8.42б) |
Если стандартное состояние NaX определяется обычным образом, так что [NaX] = l, когда NNAX = 1 ([КХ] =1, когда NKX = 1), то k = 1, и
| [NaX] = NnNaX, | (8.43a) |
| [KX] = NnKX. | (8.43б) |
Подставляя уравнение (8.43a) в уравнение (8.39), получаем
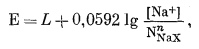 |
или
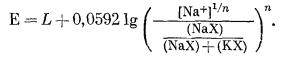 |
(8.44) |
Переписываем уравнение (8.44) в следующем виде:
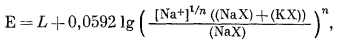 |
(8.45) |
или
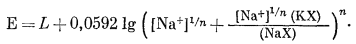 |
(8.46) |
Переписываем уравнение (8.40) в виде
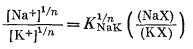 |
(8.47) |
и подставляем уравнение (8.47) в уравнение (8.4б):
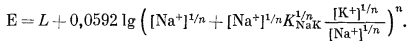 |
(8.48) |
После сокращения общего члена получим
| E = LNaK + 0,0592 lg([Na+]1/n + K1/nNaK [K+]1/n)n | (8.49) |
(где L переписывается как LNaK, чтобы яснее показать, что рассматриваемый электродный процесс является частным).
Константа LNaK обычно в литературе обозначается как Е°, но здесь она в действительности представлет собой эмпирическую константу, справедливую лишь для конкретного рассматриваемого электрода, и определяется при градуировке этого электрода. Как установлено, уравнение (8.49) точно описывает поведение стеклянных электродов [З].
В особом случае, когда n = 1, взаимное поведение NaX и КХ аналогично их поведению в идеальном растворе, и
| E = LNaK + 0,0592 lg ([Na+ + KNaK[K+]). | (8.50) |
KNaK - обменная константа реакции, называемая коэффициентом избирательности электрода. Если KNаK имеет, например, численную величину 10 и активности NaX и КХ равны, отношение [Na+] к [К+] в растворе равно 10 [уравнение (8.1)]. Если для данного электрода, чувствительного к двум одновалентным катионам, обменная константа КАВ имеет некоторое высокое значение, например 106, тогда уравнение (8.50) примет следующий вид:
| Е = LAB + 0,0592 lg [A+] + 106 [B+]. | (8.51) |
Этот результат показывает, что большая часть измеренного потенциала обусловлена величиной [В+]. Такой электрод был бы чувствительным В+-электродом.
Таким образом, обменные константы могут быть использованы для описания поведения электрода, а измерения потенциала - для определения обменных констант.
Э.д.с. д л я б о л е е ч е м д в у х к а т и о н о в. Можно вывести уравнения, характеризующие реакцию электрода при наличии более чем двух катионов, но эти соотношения нельзя проверить, за исключением особого случая, когда поверхность электрода ведет себя как идеальный раствор для всех рассматриваемых катионов (n = 1 для всех обменов).
Соответствующие уравнения для этого идеального случая с тремя ионами А+, В+ и С+ можно вывести, исходя из уравнения (8.39), помня, что h = 1 и поэтому [AX] = NAX:
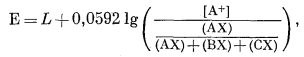 |
(8.52) |
или, преобразуя,
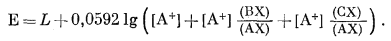 |
(8.53) |
Так как для идеального случая
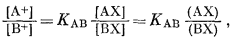 |
|
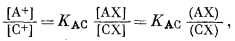 |
уравнение (8.53) можно переписать в следующем виде:
| E = LABC + 0,0592 lg([A+] + KAB[B+] + KAC[C+]). | (8.54) |
Таким образом, рассчитываемый по уравнению (8.54) потенциал соответствует потенциалу, получаемому для системы этих катионов при идеальном их поведении. Хорошо видно, что уравнение (8.54) имеет такую же форму, как и уравнение (8.50) для двух катионов. В действительности уравнение можно распространить на любое число катионов:
| E = LA ... X + 0,0592 lg([A+] + KAB[B+] + KAC[C+] + ... + KAX[X+]). | (8.55) |
Из уравнения (8.55) следует, что э. д. с. стеклянного электрода, который ведет себя идеально по отношению к ионам в растворе, представляет собой логарифмическую функцию суммы активностей ионов, причем вклад каждого катиона пропордионален величине обменной константы. Что касается физического смысла обменных констант, то они зависят от дифференциальной энергии связи ионов.
Табл. 8.1 показывает, что число ионитов, для которых n близко к единице, невелико; следовательно, уравнение (8.55) имеет ограниченное примененение.
Трудность вывода соотношения для э. д. с. в случае трех катионов заключается в том, что нельзя с уверенностью предположить, что обменная константа К'AB будет независимой от [С+] или К'AC будет независимой от [В+], как это предполагалось при выводе уравнения (8.55). Отсутствует также необходимая информация относительно изменений n в уравнении (8.1) для данного обмена в присутствии третьего иона.
Э.д.с. д л я с и с т е м ы, с о д е р ж а щ е й о д н о в а л е н т н ы й и д в у х в а л е н т н ы й к а т и о н ы и л и д в а д в у х в а л е н т н ы х к а т и о н а. Для мембранного электрода, чувствительного к двухвалентному и одновалентному катионам, мы можем написать реакцию обмена посредством уравнения (8.18)
| А2Х2 + В2+ = ВХ2 + 2А+ |
и выражение для константы равновесия посредством уравнения (8.19)
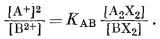 |
Соответствующее электродное уравнение для этого обмена выводится из уравнения (8.39) и имеет следующую форму:
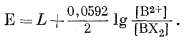 |
(8.56) |
В этой реакции участвуют два электрона; поэтому берем коэффициент 2 и получаем множитель 0,0592/2. Предполагая наличие регулярного раствора для поверхности электрода, согласно уравнению (8.43), получим
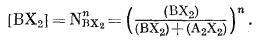 |
(8.57) |
Подставляя [ВХ2] в уравнение (8.56), получим
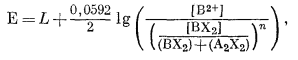 |
(8.58) |
которое после упрощения дает
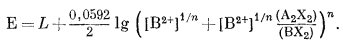 |
(8.59) |
Для регулярного раствора по уравнению (8.41)
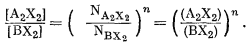 |
(8.60) |
Подставляя этот результат в уравнение (8.19), получим
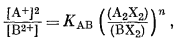 |
(8.61) |
или
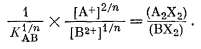 |
(8.62) |
Заменяя (A2X2)/(BX2) в уравнении (8.59) эквивалентным ему выражением из (8.62), получим
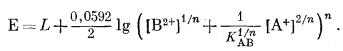 |
(8.63) |
Объединяя константу -0,0296 lgK с L, имеем, наконец,
| Е = LAB + 0,0296 lg([A+]2/n + KAB1/n [B2+]1/n)n. | (8.64) |
Это уравнение было проверено экспериментально со стеклянными мембранами в качестве электродов, и проверка показала его точность [5].
Для электрода, чувствительного к двум двухвалентным катионам, электродное уравнение аналогично уравнению (8.64):
| Е = LAB + 0,0296 lg([A2+]1/n + KAB1/n[B2+]1/n)n. | (8.65) |
Стеклянный рН-электрод, который имел такое широкое применение в течение последних 20 лет, теперь представляется особым типом мембранного электрода. Обычный рН-электрод изготовляется из натрий-кальциевого силикатного стекла и имеет относительно низкое электрическое удельное сопротивление. В рН-электроде внутри стеклянного шарика находится раствор постоянной активности Н+ с погруженным в него электродом (обычно Ag - AgCl); этот внутренний электрод проводит электроны обратимо во внутренний раствор и из него. Внешний, или испытуемый, раствор связывается с цепью эталонным электродом, например насыщенным каломельным электродом. Подробное описание см. ранее, в гл. 5.
Можно было бы ожидать, что такой электрод будет чувствителен к ионам натрия во внешнем растворе, но экспериментально установлено, что для величин рН вплоть до примерно 9 э. д. с. зависит только от активности иона водорода. Объясняется эта чувствительность к Н+ тем, что Na+ так непрочно связан со стеклом, что в большинстве водных растворов ионы натрия на внешней поверхности шарика замещаются ионами водорода. Поэтому тенденция переноса катионов способом вытеснения через стекло обусловлена не активностью Na+ в испытуемом растворе, а активностью в нем Н+.
Такая модель объясняет необходимость введения "поправки на ион натрия" в величины рН, измеренные в щелочных растворах с высокими активностями щелочных металлов. Если активность Н+ падает достаточно низко, а активность иона щелочного металла достаточно высока, часть поверхности стекла занимается ионами щелочного металла. В этом случае э. д. с. электрода будет определяться активностью и Н+ и катионов щелочного металла. Подобный эффект достаточно закономерен для введения эмпирической поправки в значения рН, полученные при измерениях в щелочных средах.
Найдено, что при изменении состава стекла относительная сила связи Н+ по сравнению со связью других катионов может быть увеличены настолько, что рН-электроды из соответствующего стекла смогут быть использованы без поправки даже в сильных растворах гидроокисей щелочных металлов.
Если поверхность стекла занята ионами водорода, электродная реакция описывается уравнением такого же типа, что и уравнение (8.36):
| Е = СH + 0,0592 lg[H+] | (8.66) |
при 25° С. Более общим уравнением, применимым при любой температуре, является уравнение
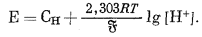 |
(8.66a) |
Так как pH = - lg[H+],
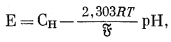 |
(8.67) |
или
| Е = СH - 0,0592рН | (8.67a) |
при 25° С.
Величина СH
различна для разных электродов и зависит от особенностей состава
используемого стекла, от стандартного раствора внутри шарика и от свойств
конкретного эталонного электрода, используемого в цепи. После градуировки
с помощью растворов с известным рН электрод можно применять для измерений
активности иона водорода в неизвестных растворах, как это описано в гл. 5.
Чувствительность стеклянного рН-электрода к катионам щелочных металлов при высоких рН позволяет предположить, что даже при низких
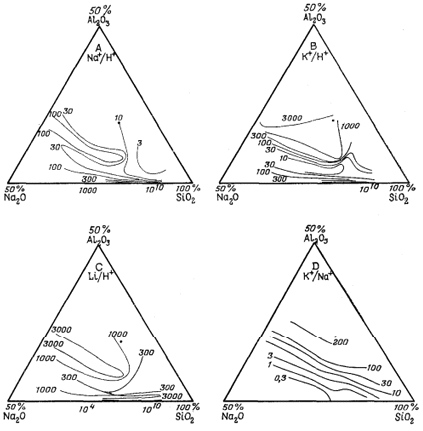 |
| Фиг. 8.8. Изолинии чувствительности электродов, характеризующие
стекла в системе Na2O - Al2O3 -
SiO2; графики даны в мольных процентах. Изолинии соответствуют таким отношениям активности К+ к активности Н+ в растворе (для D - K+/Na+), при которых поверхность электрода в равной мере занята катионом металла и Н+ (или К+ и Na+ в D), т. е. константе избирательности. Жирная точка соответствует стеклу состава 11% Na2O, 18% Аl2O3, 71% SiO2. Заимствовано с изменениями у Айзенмана, Рудина и Кэсби [З]. |
значениях рН в качестве электрода для иона щелочного металла может быть использовано стекло соответствующего состава. Эта возможность была изучена рядом исследователей; наиболее систематическим исследованием влияния состава стекла на его чувствительность к катиону является, вероятно, работа Айзенмана и его сотрудников [З]. Они изучали стекла в системе Na2O - Al2O3 - SiO2 в отношении их чувствительности как к одновалентным, так и к двухвалентным катионам. На фиг. 8.8 изображены некоторые результаты этих исследований в виде изолиний чувствительности для различных пар ионов, нанесенных на диаграмму состава стекла.
Интересно отметить влияние
небольших количеств Аl2О3 в стекле на соотношения
чувствительностей электродов к катионам различных пар. Например, обменная
константа KNаH изменяется от 1010 до 10 при
добавлении лишь нескольких процентов Al2O3. Это
значит, что реакция электрода на Na+ изменяется в
109 раз в сторону возрастания чувствительности к
Na+.
Градуировка
катионочувствительных стеклянных электродов выполняется почти так же, как
градуировка рН-электрода. Однако в связи с тем, что лишь немногие
электроды полностью избирательны к какому-либо данному иону (за
исключением тщательно контролируемых условий), для надежного перевода
найденных значений э. д. с. в величины ионных актив-ностей необходимо
произвести ряд дополнительных калибровочных операций; кроме того,
необходимо соблюдать определенные меры предосторожности.
Фиг. 8.8 показывает, что стекло, содержащее 11% Na2O и 18% Al2O3, имеет высокий коэффициент избирательности для Na+ по сравнению со всеми другими одновалентными катионами, кроме Н+. Первый шаг в применении такого электрода - установление коэффициента избирательности для Н+. Обычно это делается посредством помещения электрода в раствор соли натрия известной концентрации при 25° С и последующего титрования стандартной кислотой. Первоначальная концентрация соли натрия должна быть достаточно низка (примерно 0,01 М), чтобы для определения коэффициента активности индивидуального иона можно было уверенно применить уравнение Дебая - Хюккеля
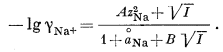 |
(2.76) |
Практически удобно пользоваться раствором 0,0112 М NaCl, в котором gNA+ = 0,895; следовательно, [Na+] = 0,0112Ч0,895 = 0,01. Для титрования обычно применяется раствор НСl; концентрация его выбирается таким образом, чтобы объем кислоты, требующийся для титрования, не очень заметно влиял на объем раствора. Измеряется э. д. с. пары Na-электрод - каломельный электрод; одновременно измеряется рН и строится график отношений этих двух переменных. Результаты типичного титрования показаны на фиг. 8.9. Кривая титрования имеет три различные области. В первой области (А на фиг. 8.9) добавление раствора НСl не оказывает измеримого влияния на э. д. с. электрода. Теоретически это область таких значений [Na+]/[H+], в пределах которых поверхность электрода почти полностью занята Na+ и не "чувствует" ионов водорода в растворе. Во второй области (В на фиг. 8.9) э. д. с. изменяется по мере добавления НСl, но на различную величину при каждом изменении рН на единицу. В этой области поверхность электрода, вероятно, занята и Na+ и Н+ и реагирует на оба катиона в испытуемом растворе. В третьей области (С на фиг. 8.9) кривая титрования представлена прямой линией и имеет наклон 0,0592 в на единицу рН. В этой области электрод ведет себя как обычный рН-электрод; его поверхность, вероятно, полностью занята Н+. При рН 3 - точке пересечения линий, соответствующих области А и области С, - электрод занят одинаково и Na+ и Н+. Поэтому, поскольку
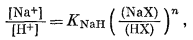 |
член справа становится равным единице, если (NaX) = (НХ), и отношение [Na+]/[H+] в растворе равно КNаH - константе обмена, или коэффициенту избирательности. Для указанного титрования одинаковая занятость
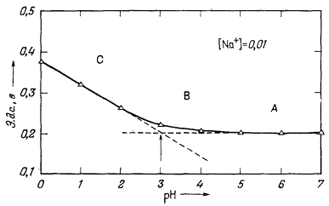 |
| Фиг. 8.9. Кривая титрования, использованная при выводе уравнения
для стеклянного электрода. Сплошная линия проведена на основе результатов замеров э. д. с. при различных рН, полученных добавлением НСl к раствору с [Na+] = 0,01. Треугольниками показаны значения, рассчитанные по уравнению Е = 0,318 + 0,0592 lg([Na+] + 10[Н+]). |
наступает при [Na+] = 0,01 и [Н+] = 0,001 (рН = 3), поэтому коэффициент избирательности равен 10.
Электродное уравнение можно вывести из числовых данных. Так как
| Е = LNaH + 0,0592 lg([Na+]1/n + К1/nNaH [Н+]1/n)n, | (8.68) |
начальная э. д. с. (область А на фиг. 8.9) при фактическом отсутствии Н+ равна
| E = LNaH + 0,0592 lg[Na+]. | (8.69) |
Подставляя 0,200 для Е и 0,01 для [Na+], получим
| 0,200 = LNaH + 0,0592 lg 0,01, | |
| LNaH = 0,318 в. |
Подставляя это значение LNaH и KNaH = 10 в уравнение (8.68), получим
| Е = 0,318 + 0,0592 lg([Na+]1/n + 101/n [Н+]1/n)n. | (8.70) |
Наконец, величины Е можно рассчитать для различных значений рН, предполагая, что n равно единице. Такие рассчитанные точки изображены в виде треугольников на фиг. 8.9. Согласие с наблюдаемыми величинами показывает, что электрод ведет себя как идеальный обменный субстрат, для которого n = 1. Таким образом, поведение электрода можно описать конечным уравнением
| Е = 0,318 + 0,0592 lg([Na+] + 10 [H+]). | (8.71) |
К счастью, катионочувствительные стеклянные электроды
ведут себя сходным образом с большинством катионных пар, и для этих
электродов n близко к единице. Простейший метод определения
n путем градуировочного титрования - сравнение наблюдаемых
соотношений с серией кривых, рассчитанных для различных значений
n1 (стр.246).
Уравнение для натриевого электрода [(8.71)] показывает, что в пределах значительного интервала колебаний состава раствора э. д. с. является функцией и Na+ и Н+. В растворе с [Na+] = 0,01 электрод работает как рН-электрод при рН ниже 2 и как Na+-элeктpoд при рН выше 4 (фиг. 8.9). Между рН 2 и рН 4 он имеет смешанные функции. Однако для измерений рН в этой области можно, не опасаясь помехи со стороны Na+, использовать обычный рН-электрод. Установленная с его помощью величина [Н+] может быть подставлена в уравнение (8.71) для нахождения [Na+]. Аналогично в случае растворов, содержащих Na+ и К+, при значениях рН, слишком высоких, чтобы мог мешать Н+, электрод пригоден для измерений Na+ в присутствии К+ (KNaK @ 0,04) и может быть использован в соединении с электродом, в какой-то мере избирательным по отношению к К+ (т. е. КNаK @ 4), для нахождения [К+].
Если электроды нужно применить в растворах двух катионов, в которых оба электрода имеют смешанную функцию, активности катионов можно определить путем совместного решения электродных уравнений при условии, конечно, достаточного различия в избирательности электродов.
Наконец, рассмотрим особый случай определения активностей Na+ и K+ в растворе КСl и NaCl, когда имеются два электрода из стекол различного состава. Предположим, что ни тот, ни другой электрод не обнаруживают чувствительности к Н+ выше рН 5, а испытуемый раствор имеет рН 7. Электрод А градуируют, помещая его в раствор NaCl с известной активностью Na+ и затем титруют раствором КС1, чтобы определить коэффициент избирательности электрода; аналогичная процедура проделывается для электрода В. В результате получим уравнения (n = 1)
| ЕA = 0,300 + 0,0592 lg([Na+] + 5,0[K+]), | (8.72а) |
| ЕB = 0,250 + 0,0592 lg([Na+] + 0,1 [К+]). | (8.72б) |
Затем измеряется неизвестный раствор. Допустим, найдено, что ЕA равно 0,283, а ЕB - 0,150 в. Сделав соответствующую подстановку и преобразовав уравнения, находим
| [Na+] + 5,0 [К+] = 10(0,282 - 0,300)/(0, 0592), | (8.73а) |
| [Na+] + 0,1 [К+] = 10(0,150 - 0.,250)/(0,0592). | (8.73б) |
Исключаем [Na+] и решаем уравнение для [К+]:
| 4,9 [К+] = 0,50 - 0,02 = 0,48, | |
| [К+] = 0,1. |
Подставляя в уравнение (8.73), получим
| [Na+] = 0,01. |
|
1 (стр.246) Авторы благодарят д-ра Айзенмана за сообщение об этом методе. |
Э л е к т р о д ы, ч у в с т в и те л ь н ы е к к а т и о н а м щ е л о ч н о з е м е л ь н ы х м е т а л л о в. В последнее время найдены составы стекол, пригодных для изготовления стеклянных мембранных электродов, чувствительных к двухвалентным катионам [5]. Эти стекла представляют собой четвертные системы, в составе которых количество SiO2 колеблется от 50 до 90 мольных процентов, а остающиеся 50-10 мол.% приходятся на окислы одновалентных, двухвалентных и трехвалентных катионов, т. е. К2О, ВаО и Al2O3.
Установлено, что такие электроды строго подчиняются уравнению (8.65)
| Е = LAB + 0,0296 lg([A2+]1/n + KAB1/n [В2+]1/n)n |
для пар двухвалентных катионов и что для этих пар n @ 1, а КAB изменяется от приблизительно 1,5 до 1. Электроды избирательны по отношению к щелочноземельным катионам в последовательности Ва2+ > Sr2+ > Са2+ > Mg2+. Это означает, что для любой пары ионов в приведенной последовательности КАВ > 1, если А стоит справа от В. Например, для типичного электрода KMgCа = 1,5, так что
| Е = LMgCa + 0,0296 lg([Mg2+] + 1,5 [Са2+]). |
Чувствительные к двухвалентным катионам электроды будут реагировать и на одновалентные катионы, содержащиеся в растворе. Все же наблюдаемая э. д. с. не всегда соответствует рассчитываемой по уравнению (8.64)
| Е = LAB + 0,0296 lg([A+]2/n + K1/nAB [В2+]1/n)n, |
но в некоторых случаях подчиняется эмпирическому уравнению
| Е = LAB + 0,0296 lg([А+]2m/n + K1/nAB [В2+]1/n)n. | (8.74) |
Найдено, что m отличается от единицы для толстых электродов. Однако, если стеклянная мембрана достаточно тонка и электрод должным образом подготовлен смачиванием в интересующем нас растворе электролита, значение m будет равно единице.
Грегор [6] по-иному подходит к проблеме изготовления электродов, пригодных для измерения низких концентраций ионов двухвалентных металлов в присутствии умеренных и высоких концентраций одновалентных ионов. Он заметил, что стеараты прочно связывают кальций, стронций и барий, в то же время слабо удерживая ионы щелочных металлов. Однако при комнатной температуре стеараты представляют собой гидратированные соединения, и невозможно изготовить стеаратное стекло таким образом, чтобы сохранить непрерывную жесткую структурную решетку. Грегор решил проблему непрерывной решетки, нанося последовательно мономолекулярные слои стеаратов различных двух- и трехвалентных катионов на стеклянную подложку. Эти электроды работают хорошо, если используются для измерения растворов, содержащих только тот ион, который входит и в состав стеарата, обволакивающего мембрану. Например, стеарат кальция обнаруживает реакцию, описываемую электродным уравнением [см. уравнение (8.31) с nX- = 2], если используется в растворах хлорида кальция даже с высоким содержанием CaCl2.
К сожалению, удельный объем стеаратов возрастает по мере уменьшения энергии связи катиона. Грегор нашел, например, что электроды из стеарата кальция при погружении в концентрированные растворы Na+ обычно набухают и в связи с этим разрушаются. По энергиям связи и удельным объемам изученные стеараты образуют следующие ряды:
энергия связи: Fe3+ > Ва2+ >
Sr2+ > Са2+ > Mg2+ >
Na+,
удельный объем: Fе3+ < Ва2+
< Sr2+ < Са2+ < Mg2+ <
Na+.
Таким образом, электрод из
стеарата трехвалентного железа избирателен для иона трехвалентного железа
в присутствии любого из прочих ионов приведенного ряда, но в присутствии
любого из этих ионов будут происходить разбухание стеарата трехвалентного
железа и, следовательно, разрушение его жесткой структуры. Аналогичным
образом электрод из стеарата кальция избирателен для Са2+ по
сравнению с Mg2+ и Na+, но будет реагировать на
Sr2+, Ва2+ и Fe3+. Кроме того, электрод
из стеарата кальция в присутствии Sr2+, Ba2+ или
Fе3+ обычно дает усадку. Усадка разрушает электрод так же
энергично, как и разбухание. Грегор изготовил электроды из стеарата
кальция, которые работали избирательно как кальциевые электроды при
довольно высоких отношениях Na+/Ca2+, использовав
тиски для предотвращения разбухания. Однако технические трудности до сих
пор препятствуют широкому производству и применению стеаратных электродов.
Катиониты подчиняются соотношениям
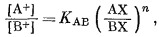 |
(8.1) |
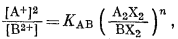 |
(8.17) |
где [А+] и [В+] или [В2+] -активности ионов в растворе, (АХ), (ВХ), (BX2) или (A2X2) - концентрации ионов в ионите, КAB - константа обмена, или избирательности, а n = 1 - В/2RT - показатель степени, обычно близкий к единице, но колеблющийся по величине от 0,25 до 5,0. Эти уравнения выводятся на основании закона действия масс. При этом предполагается, что обменный субстрат образует регулярный раствор.
Стеклянные электроды, чувствительные к одновалентным катионам, при 25° С подчиняются эмпирическому уравнению для напряжения Е:
| Е = LAB + 0,0592 lg([A+]1/n + K1/nAB [B+]1/n)n. | (8.49) |
Для одно-двухвалентных систем уравнение имеет вид
| Е = LAB + 0,0296 lg([A+]2/n + K1/nAB [B2+]1/n)n. | (8.64) |
Для двух-двухвалентных систем
| Е = LAB + 0,0296 lg([A2+]1/n + K1/nAB [B2+]1/n)n. | (8.65) |
LAB - эмпирическая константа, характерная для каждого отдельного электрода. Эти уравнения для э. д. с. выводятся на основании обычных уравнений Полуячеек и эмпирических уравнений обмена, приведенных выше.
Стеклянные электроды могут быть использованы для измерения активностей отдельных одновалентных или двухвалентных катионов в растворах, содержащих несколько катионов, путем применения стеклянных электродов различных составов и, следовательно, различных избирательностей по отношению к нескольким имеющимся катионам.
Электроды, изготовленные из стеаратов, пригодны для измерения активностей щелочноземельных катионов в однокатионных растворах; технические, трудности пока препятствуют их применению в полиионных растворах.
Как было показано выше,
ионный обмен и мембранные электроды представляют собой две стороны одного
и того же явления, необходимой предпосылкой которого служит наличие
жестких отрицательно заряженных решеток, допускающих привнес, вынос или
перемещение катионов без разрушения решетки.
А. Катионный обмен 8.1. При условии
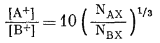
построить график зависимости lg
([A+]/[B+]) (ордината) от lg
(NAX/NBX).
а) Чему
равен наклон полученной линии? б) Чему равен отрезок, отсекаемый линией на
оси ординат?
Ответ: а) наклон = 1/3; б) отрезок
= lg 10.
8.2. Чему равно отношение
[А+] к [В+] в предыдущем упражнении, если
NAX = NBX?
Ответ:
10.
8.3. Если ионит ведет себя как
идеальный бинарный раствор, чему равна активность ВХ при NAX =
0,3?
Ответ: аBX =
0,7.
8.4. Если ионит ведет себя как
регулярный раствор, для которого В равно 0,70 ккал/моль при
25° С, чему равна активность АХ при NAX =
0,30?
Ответ: aАХ =
0,54.
8.5. Если равновесие для ионита в
упражнении 8.4 представить в виде
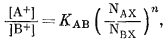
чему приблизительно будет равна величина n при 25°
С?
Ответ: n =
0,41.
8.6. Некоторый монтмориллонит имеет
KNаK = 2,5 при 25° С и ведет себя как идеальный раствор
в процессе обмена. Этот монтмориллонит находится в равновесии с подземной
водой, которая из катионов в значительных концентрациях содержит только
Na+ и К+. Ионная сила воды приблизительно равна
0,01, и вода содержит 230 ч. на млн. Na+ и 39 ч. на млн.
К+. Чему равно отношение Na+ к K+ на
обменных местах в монтмориллоните при 25°
С?
Ответ: (NaX)/(KX) =
4.
8.7. Образец монтмориллонита при 25° С
взаимодействует с растворами, содержащими Са2+ и
Na+. Его поведение описывается уравнением
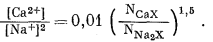
Чему равно отношение [Ca2+]/[Na+] в
растворе при равновесии, если NCaX =
NNa2X?
Ответ:
Неопределенно. Должны быть указаны [Са2+] или
[Na+].
8.8. Чему равно
NCaX/NNa2X для монтмориллонита из
упражнения 8.7,
а) Если [Са2+]
= 0,01 и [Na+] = 0,01?
б) Если
[Са2+] = 0,01 и [Na+] =
0,10?
в) Если [Са2+] = 0,01 и
[Na+] = 10?
Ответ: а)
102,67; б) 101,33; в)
10-1,33.
8.9. Какие ионы -
катионы щелочных металлов или щелочных земель- должны были бы занимать
большую часть обменных мест, если бы тот же самый монтмориллонит находился
в виде взвеси в средней речной
воде?
Ответ: Щелочноземельные
катионы.
Б. Катионные
электроды
8.10. При измерении рН чему
равно изменение э. д. с. пары стеклянный электрод - каломельный электрод
при 25° С, если рН изменяется на 2 единицы
?
Ответ: 0,118
в.
8.11. Если внутренний раствор
стеклянного электрода (раствор 0,1 н. НСl) начинает испаряться из-за
утечки, в каком направлении - в сторону увеличения или уменьшения - будет
предположительно изменяться рН раствора постоянного
состава?
Ответ: рН, по-видимому, будет
возрастать.
8.12. Стеклянный электрод,
чувствительный к ионам натрия, используется вместе с насыщенным
каломельным электродом в двух растворах NaCl. Первый раствор имеет
известную [Na+] = 10-3 и дает э. д. с. 0,2231
в при 25° С. Наблюдаемая э. д. с. второго раствора равна 0,3242
в.
а) Чему равна [Na+]
во втором растворе?
б) Чему
приблизительно равно
МNа+?
Ответ:
а) [Na+] = 10-1,29; б) gNа+ @
0,83, MNa+ @
0,06.
8.13. Поведение электрода,
чувствительного одновременно к Na+ и К+, описывается
при 25° С уравнением
ЕNаK = 0,5002 + 0,0592 lg([Na+] + 4,0[К+]).
Второй электрод, чувствительный только к Na+,
подчиняется уравнению ENa = 0,4921 + 0,0592 lg[Na+].
Если в данном растворе при 25° С ENa = 0,3737 в и
ENaK = 0,4231 в, чему равны активности Na+ и
К+?
Ответ: [Na+] =
0,01, [К+] = 0,01.
8.14.
Электрод, чувствительный к Na+ и К+, помещается в
раствор, содержащий Na+ с активностью 0,001 при 25° С. Затем
раствор титруется раствором калиевой соли. Ниже приведены значения Е как
функции активности добавляемого К+ (при постоянной
[Na+]):
| [Na+] | [К+] | ЕNаК, в |
| 0,001 | 0,0 | 0,3226 |
| 0,001 | 0,0001 | 0,3293 |
| 0,001 | 0,001 | 0,3582 |
| 0,001 | 0,01 | 0,4109 |
| 0,001 | 0,1 | 0,4701 |
Построить график зависимости ЕNаK (ордината)
от lg [K+]. По графику
определить:
а) коэффициент
избирательности КNаK для
электрода;
б) работает ли электрод как
идеальный или регулярный раствор?
Ответ:
а) КNaK = 3,6; б) идеальный
раствор.
8.15. Стеклянный электрод,
чувствительный к Na+, К+ и Li+, работает
при 25° С в растворах NaCl согласно уравнению
ENA = 0,2500 + 0,0592 lg[Na+].
Если КNаK = 0,1 и KNaLi = 2,0, чему
равно ENaKLi при 25° С в растворе с [Na+] = 0,01,
[К+] = 0,1 и [Li+] = 0,02?
Электрод по отношению
к этим ионам ведет себя как идеальный
раствор.
Ответ: ЕNаKLi =
0,1777 в.
8.16. Для описанного в
упражнении 8.15 электрода, чему равно DF°реакции при 25° С для обменного
равновесия
LiXстекл + Nа+водн = NaXстекл + Li+водн.
Ответ: DF°реакции = 0,411
ккал.
8.17. В морской воде
[Na+] = 0,35 и [Са2+] = 0,003. Имеется два
электрода, один из которых полностью избирателен для Na+, а
другой чувствителен лишь к Na+ и Са2+. Последний
электрод имеет KCaNa = 20 при 25° С. Можно ли эти
электроды использовать совместно для измерения [Са2+] в морской
воде при 25° С, если применяемый вольтметр имеет точность 0,1 мв?
Объясните ответ.
Ответ: Нет, необходима
гораздо большая чувствительность.
8.18.
Образец обычной водопроводной воды содержит 9 ч. на млн. Na+, 1
ч. на млн. К+, 20 ч. на млн. Са2+ и 5 ч. на млн.
Mg2+ и имеет ионную силу 0,003. Можно ли электрод, имеющий
KCaMg = 1, KCaNa = 20 и
КCaK = 10, использовать для измерения общей жесткости
(Са + Mg) с точностью до ±2%, если не вводить никаких поправок на
присутствие ионов Na и К?
Ответ: Да.
Поправки на натрий и калий несущественны. 2%-ное изменение концентрации Са
+ Mg будет изменять измеряемую э. д. с. приблизительно на 1 мв.
1. C a r r o l l D. Ion exchange in clays and other
minerals, Bull. Geol. Soc. Am., 70, 754, 1959.
2. E i s e n m a n G. On
the elementary origin of equilibrium ionic specificity, in Symposium on
Membrane Transport and Metabolist, Kleinzeller A., Kotyk A. (eds.), New
York, Academic, 1962.
3. E i s e m n a m G., R о u d i n D. О., С a s b
у J. U. Science, 126, 831, 1957.
4. G a r r е 1 s R. M., С h r i s t C.
L. Am. Journ. Sci., 254, 372, 1956.
5. G a r r e l s R. M., S a t о M.,
T h o m p s o n M. E., T r u e s d e l l A.H. Science, 135, 1045,
1962.
6. G r e g o r H.P., S c h o n h o r n H. Multilayer membrane
electrodes, Journ. Am. Chem. Soc., 709, 1507, 1957.
7. W a 1 t о n H.
F. Ion exchange equilibria, in Ion Exchange Theory and Practice, Nachod
F.C. (ed.), New York, Academic, 1949.
К е 1 1 у W. P. Cation Exchange in Soils (АСА Monograph
109), New York, Reinhold, 1948.
M a r s h a l l C.E. The Colloid
Chemistry of the Silicate Minerals, New York, Academic, 1949.
S a l m o
n J.E., H a l e D.K. Ion Exchange, A Laboratory Manual, New York,
Academic, 1959. (Обратить особое внимание на гл. 3: Properties of ion
exchange resins.)
S c h a c h t s c h a b e l P. Untersuchungen uber
die sorption der tonmineralien und Bodenkolloide, und die Bestimmung des
Anteils dieser Kolloide und der sorption im boden, Kolloid Beih., 51, 199,
1940.
W а 1 t о n H. F. Ion exchange equilibria, in Ion Exchange Theory
and Practice, Nachod F.C. (ed.), New York, Academic, 1949.
W i k l a n
d e r L a m b e r t. Cation and anion exchange phenomena, in Chemistry of
the Soil, Firman E. Bear (ed.) (АСА Monograph 126), New York, Reinhold,
1955.
B o w e r С. A. Determination of sodium in saline
solutions with a glass electrode, Proc. Soil. Sci. Am., 23, 29, 1959.
E
i s e n m a n G e o r g e. Cation selective glass electrodee and their
mode of operation, Biophysical Journ., 2, pt. 2 (suppl.), 259, 19P2.
E
i s e n m a n G. On the elementary origin of equilibrium ionic
specificity, in Symposium on Membrane Transport and Metabolism,
Kleinzeller A., Kotyk A. (eds.), New York, Academic, 1962.
E i s e n m
a n G., R u d i n D. О., С a s b у J. U. Glass electrode for measuring
sodium ion, Science, 126, 831, 1957.
Ф е д о т о в Н.А. Электродные
свойства литиевого стекла. Журнал физ. химии, 32, № 9, 1951, 1958.
F r
i e d m a n S.M., J a m i e s o n J.D., N a k a s h i m a M., F r i e d m
a n C.L. Sodium- and potassium-sensitive glass electrodes for biological
use. Science, 130, 1252, 1959.
G a r r e 1 s R. M., S a t o M., T h o m
p s о n M. E., Т г u e s d e 11 A. H. Glass electrodes sensitive to
divalent cations, Science, 135, 1045, 1962.
Г о р е м ы к и н В. Э., К
р ю к о в П. А. Потенциометрический метод определения ионов натрия при
помощи стеклянного электрода с натриевой функцией, Изв. АН СССР, отд. хим.
наук, № 11, 1387, 1957.
I s a r d J. 0. Alkali ion determination by
means of glass electrodes, Nature, 184, 1616, 1959.
К р ю к о в П. А.,
Ш у л ь ц M. M., Г о р е м ы к и н В.Э. 0 возможности применения
стеклянных электродов с натриевой функцией при анализе вод,
Гидрогеохимические материалы, 24, 23, 1955.
Н и к о л ь с к и й Б.П., Ш
у л ь ц М.М., П о ш е х о н о в а Н.В. Теория стеклянного электрода. VII.
Влияние посторонних ионов на натриевую и калиевую функцию стеклянных
электродов. Журнал физ. химии, 32, № 1, 19, 1958.
Н и к о л ь с к и й
Б. П., Ш у л ь ц М.М., П о ш е х о н о в а Н.В. Теория стеклянного
электрода. VIII. Переход стеклянных электродов от одной металлической
функции к другим. Журнал физ. химии, 32, № 2, 262, 1958.
Ш у л ь ц M.
M. Исследование натриевой функции стеклянных электродов, Уч. зап. ЛГУ, №
169, сер. хим. наук, вып. 13, 80, 1953.
Б е л и н с к а я Ф. А., М а т е р о в а E. А.
Электродные свойства ионитовых мембран, Вестник ЛГУ, № 16, сер. физ. и
хим., вып. 3, 85, 1957.
F i s c h e r R.B., B a b c o c k R.F.
Electrodes consisting of membranes of precipitates, Anal. Chem., 30, 1732,
1958.
G г e g о г H. P., S c h o n h o r n H. Multilayer membrane
electrodes, Journ. Am. Chem. Soc., 79, 1507, 1957.
G r e g o r H. P., S
c h o n h o r n H. Multilayer membrane electrodes II, Preparation and use
in double concentration cells, Journ. Am. Chem. Soc., 81, 3911, 1959.
M
a r s h a l l C.E. The electrochemical properties of mineral membranes,
Journ. Am. Chem. Soc., 63, 1911, 1941.
S о 1 1 n e r К. Recent advances
in the electrochemistry of membranes of high ionic selectivity, Journ.
Electrochem. Soc., 97, 139C, 1950.
|
|
|
|
[Содержание] [Глава 7] [Глава 9] |