| Р.М. Гаррелс, Ч.Л. Крайст | Растворы, минералы, равновесия |
|
|
|
|
[Содержание] [Глава 8] [Глава 10] |
|
|
|
|
Вся разобранная выше методика расчета соотношений устойчивости при 25° С (298,15° К) и 1 атм общего давления может быть использована для изучения систем при иных температурах и давлениях, если только в распоряжении исследователя будут необходимые термодинамические данные для интересующих его конкретных условий. Однако если для низких температур и давлений такие данные имеются и их можно непосредственно использовать при построении диаграмм, то для повышенных температур и давлений аналогичные сведения чрезвычайно скудны. Поэтому при построении диаграмм обычно приходится прибегать к расчетам свободной энергии, пользуясь методиками самой различной достоверности.
В настоящей главе мы
рассмотрим некоторые из этих методик, проиллюстрируем их примерами расчета
величин свободной энергии при повышенных температурах, а также построим
несколько диаграмм для высоких температур и давления 1 атм. В
заключение коснемся вопроса об изменении термодинамических параметров при
повышении общего давления.
Чтобы рассчитать устойчивые отношения между соединениями при некоторой повышенной температуре и 1 атм общего давления, необходимо определить стандартные свободные энергии соответствующих реакций при этой температуре. В идеальном случае в распоряжении исследователя могут оказаться таблицы стандартных свободных энергий образования соединений, растворенных компонентов и элементов (если только они даны не для эталонных состояний) для всех интересующих его температур или же таблицы свободных энергий, рассчитанных с небольшими температурными интервалами, которые допускают несложную и достаточно точную интерполяцию. Вооружившись такими таблицами, исследователь может провести необходимые расчеты по схеме, аналогичной той, которая была ранее рассмотрена для 298,15° К. Вместо таблиц можно использовать значения DF°обр для всех компонентов, данные в виде алгебраических функций температуры или в виде графиков.
Из-за фрагментарности и неполноты имеющихся данных не всегда удается собрать все необходимые сведения, которые были бы одинаково удовлетворительны. И тогда приходится использовать различные данные, точность которых колеблется от превосходной (в том случае, если они приведены в виде аналитических функций или таблиц для малых приращений температуры) до просто хорошей или даже низкой (если эти данные получены путем различного рода вычислений).
Ниже мы кратко рассмотрим
несколько известных в литературе способов выражения величины DF°обр - как прямых, так и с помощью
некоторых функций.
Для любой химической реакции справедливо следующее выражение:
| DF°реакции = DH°реакции - DTS°реакции, | (9.1) |
где DF°реакции - изменение стандартной свободной энергии, DH°реакции - изменение энтальпии, или теплосодержания, а DS°реакции - изменение энтропии. Символ °, как всегда, указывает, что каждая из входящих в уравнение величин DF°реакции, DH°реакции и DS°реакции соответствует стандартным условиям, т. е. определена при фугитивности, равной единице, и температуре Т. Температура может быть любой, но одинаковой для каждой из трех термодинамических переменных.
Если бы были известны интересующие нас значения DH°реакции и DS°реакции для различных температур, то рассчитать соответствующую величину DF°реакции, безусловно, было бы совсем нетрудно: для этого достаточно было бы использовать уравнение (9.1). Прежде чем вникнуть в суть данной проблемы, разъясним природу величин DH°реакции и DS°реакции. Для наших целей более детальное рассмотрение термодинамического смысла этих величин не нужно; нам понадобятся лишь их численные значения, необходимые при вычислениях изменения свободной энергии1 (стр.254).
Э н т а л ь п и я. Изменение энтальпии, происходящее в ходе изотермической реакции при постоянном общем давлении2 (стр.254), равно сумме тепла, поглощенного при этой реакции. Например, для реакции
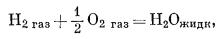 |
|
| DH°реакции 298,15 = -68,3174 ккал. | (9.2) |
Эта запись означает, что теплота реакции DH°реакции при 298,15° К (25° С) и 1 атм общего давления равна -68,3174 ккал/моль. Знак минус, стоящий перед величиной DH°реакции, указывает на выделение теплоты при реакции.
Теплота образования
какого-либо соединения (или элемента в нестандартном состоянии)
определяется теплотой, поглощенной при реакции образования этого
соединения из отдельных элементов в их стандартном состоянии3 (стр.254) при любой
данной температуре; эта теплота обозначается символом DH°обр. Принято, что теплота
образования элемента в его стандартном состоянии равна нулю. Чтобы
отразить все эти условия, еще раз напишем
|
1 (стр.254) Для более детального ознакомления с понятиями, затрагиваемыми в гл. 9, читатель может обратиться, например, к книге Клотца [9]. 2 (стр.254) Для всех процессов или реакций термодинамические функции DF, DH и DS определяются лишь начальным и конечным состояниями взаимодействующих веществ и не зависят от того, каким образом этот процесс совершается. Следовательно, упоминание о постоянной температуре и постоянном давлении для реакции имеет лишь тот смысл, что температура или давление были одинаковы для начального и конечного состояний данных веществ. 3 (стр.254) В случае энтальпии и энтропии, как и при определении свободной энергии, за стандартное состояние чистого твердого или жидкого вещества принята наиболее стабильная форма этого вещества при 1 атм и данной температуре (если только не вводятся какие-либо иные условия). В случае чистого газа энтропия отнесена к гипотетическому идеальному газу с давлением 1 атм, когда энтальпия характеризуется той же величиной, что и энтальпия реального газа при нулевом давлении. В подобных условиях DF°обр, DH°обр и DS°обр обладают значениями, отнесенными к одному и тому же стандартному газу с фугитивностью, равной единице. Для растворов аналогичные определения более сложны; см., например, работу Клотца [9, гл. 19]. |
реакцию (9.2), но уже в развернутом виде:
| H2 | + | 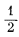 |
O 2 | = | H2O, |
| (газ при 298,15° К и нулевом давлении) |
(газ при 298,15° К
и вулевом давлении) |
(жидкость при 298,15° К и 1 атм давления) | |||
DH°реакции = DH°обр H2O - DH°обр H2 - 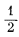 DHобр O2 = -68,3174
- 0 - 0, DHобр O2 = -68,3174
- 0 - 0, | |||||
| DH°обр H2O = -68,3174 ккал/моль | |||||
Теплоту реакции можно вычислить по табличным данным теплот образования DH°обр таким же образом, как мы это делали при определении DF°реакпии по значениям DF°обр (гл. 1). Для любой реакции при температуре Т
| DH°реакпии = sDH°обр продуктов реакции - sDH°обр реагентов. | (9.2а) |
В качестве примера рассчитаем теплоту гидратации корунда до гиббсита при 298,15° К. Составляем уравнение реакции:
| Al2O3 крист | + | 3Н2Ожидк | = | Аl2О3 Ч 3Н2Окрист, |
| корунд | гиббсит |
и далее
| DH°реакпии = DH°обр гиббсита - DH°обр корунда -3DH°обр Н2О. | (9.3) |
Значения DH°обр 298 для ряда веществ приведены в приложении 2; найдя соответствующие величины для уравнения (9.3), получим
| DH°реакпии = -613,7 - (-399,09) - 3 ґ (-68,317), | |
| DH°реакпии = -9,66 ккал/моль. | (9.3а) |
Изменение энтальпии вещества с температурой при постоянном давлении равно теплоемкости1 (стр.255) СP этого вещества. Таким образом,
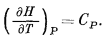 |
(9.4) |
Частное интегрирование уравнения (9.4) дает следующий результат:
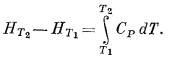 |
(9.5) |
Правую часть уравнения (9.5) можно рассчитать различными способами. На небольшом интервале температур или вообще при постоянной величине СP уравнение (9.5) принимает вид
| HT2 - HT1 = CP (T2 - T1). | (9.6) |
Обычно интеграл уравнения (9.5) рассчитывают путем графического изображения экспериментально определенных величин СP относительно Т; измерение площади от T1 до T2 под полученной кривой даст величину разности HT2 - HT1.
Теплоемкость вещества СP можно также представить в виде эмпирического уравнения, которое, будучи подставлено в уравнение (9.4), даст возможность решить его. Если СP подчиняется выражению
| СP = a + 2bТ - сТ -2, | (9.7) |
|
1 (стр.255) Теплоемкость вещества определяется числом калорий, необходимых для повышения температуры этого вещества на 1° С. |
то соответствующее ему уравнение энтальпии примет следующую общую форму:
| HT - HT' = аT + bТ2 + сT-1 + d. | (9.8) |
Это уравнение с четырьмя константами предложено Мейером и Келли [12] как уравнение, отвечающее огромному большинству веществ для температур выше начальной Т' = 298,15° К. Значения H и СP в этих уравнениях справедливы для любых давлений. Если для каждого значения Т измерения производятся над веществом при фугитивности, равной единице, то величина H в уравнениях (9.4) - (9.8) повсеместно заменяется величиной H°, а СP - величиной СP°.
Значения H°T - H°298 для температур, превышающих 298,15° К, обычно сводятся в таблицы, одну из которых - для силлиманита - мы приводим (табл. 9.1); в ней же даются соответствующие величины энтропии (рассмотрению которой будет посвящен следующий раздел). В случае силлиманита наблюдается хорошее соответствие уравнениям теплосодержания (9.8) и теплоемкости (9.7). Табл. 9.1 заимствована из работы Келли [б], в кото-
Т а б л и ц а. 9.1
| T, °K | HT1 -
H298,15, кал/моль |
S°T -
S°289,15, кал/град. моль |
T, °K | HT1 -
H298,15, кал/моль |
S°T -
S°289,15, кал/град. моль |
| 400 | 3300 | 9,49 | 1100 | 33400 | 52,06 |
| 500 | 6940 | 17,60 | 1200 | 37900 | 55,98 |
| 600 | 10900 | 24,82 | 1300 | 42500 | 59,66 |
| 700 | 15300 | 31,60 | 1400 | 47000 | 62,99 |
| 800 | 19900 | 37,74 | 1500 | 51600 | 66,17 |
| 900 | 24400 | 43,03 | 1600 | 56300 | 69,20 |
| 1000 | 28900 | 47,77 | |||
|
Al2SiO5
(силлиманит): | |||||
рой приводятся данные для 893 элементов и неорганических соединений, многие из которых представляют определенный геохимический интерес.
Разность H°T2 - H°T1 не следует путать с теплотой образования DH°обр. Первая величина представляет собой изменение теплосодержания вещества при изменении его температуры от T1 до Т2, DH°обр - это изменение теплосодержания при образовании какого-либо соединения из элементов при постоянной температуре Т. В частности, DH°обр для данного элемента в его стандартном состоянии равно нулю при каждой данной температуре, тогда как для того же элемента HT2 - HT1 № 0.
Согласно правилам дифференциального исчисления, мы можем перейти от ранее рассмотренных уравнений с величиной H к аналогичным уравнениям с величиной H°реакции. Производное от уравнения (9.4), отвечающее изменению теплоты реакции с температурой при постоянном давлении, будет иметь следующий вид:
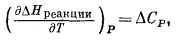 |
(9.9) |
где
| DСP = sCP продуктов реакции - SCР реагентов. | (9.9a) |
Нижний индекс P указывает лишь на то, что давление на каждое вещество, участвующее в реакции, одинаково при каждой рассматриваемой температуре. Таким образом, если мы знаем DHреакции для превращения 1 моль жидкой воды под давлением 10 атм в водяной, пар с давлением 1 атм при температуре T1, то уравнение (9.9) поможет нам рассчитать DHреакпии для того же процесса при некоторой другой температуре Т2.
Частное интегрирование уравнения (9.9) дает такой результат:
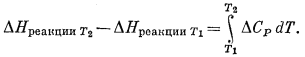 |
(9.10) |
На небольшом интервале температур или вообще, если DСP можно считать постоянной,
| DHреакции T2 - DHреакции T1 = DСP (Т2 - T1). | (9.11) |
В общем случае если графически изобразить зависимость DСP данной реакции от температуры, то в соответствии с уравнением (9.10) площадь под полученной кривой от Т1 до Т2 будет равна
| DHреакции T2 - DHреакции T2 |
Если СP каждого вещества, принимающего участие в реакции, представить в виде эмпирического уравнения типа (9.7), то, согласно формуле (9.9),
| DCP = Da + 2DbT - DсT -2. | (9.12) |
Подстановка уравнения (9.12) в уравнение (9.9) после интегрирования дает следующий результат:
| DHреакции = DHI + DaT + DbT 2 + DсT -1, | (9.13) |
где DHI - постоянная интегрирования. Уравнение (9.13) аналогично уравнению (9.8).
Если измерения над всеми рассматриваемыми веществами проводилось при фугитивности, равной единице, то DСP повсюду можно заменить на DС°P, а DH - на DH°.
В качестве иллюстрации использования уравнений (9.12) и (9.13) рассчитаем теплоту следующей реакции (при 1000° К):
|
(9.14) |
С этой целью воспользуемся данными Келли [6]. Уравнения СP для H2S, Н2 и S2 в этой работе находятся соответственно на стр. 82, 79 и 181. Эти уравнения таковы:
| Н2Sгаз: С°P = 7,81 + 2,96 ґ 10-3Т - 0,46 ґ 105T -2, | |
| Н2 газ: С°P = 6,52 + 0,78 ґ 10-3 + 0,12 ґ 105T -2, | |
| S2 газ: C°P = 8,72 + 0,16 ґ 10-3T - 0,90 ґ 105T -2. |
На основании этих соотношений рассчитаем коэффициенты для уравнения (9.13):
Dа = 7,81 - 6,52 - 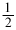 (8,72) = -3,07, (8,72) = -3,07, |
|
2Db = [2,96 - 0,78 -
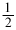 (0,16)]
10-3 = 2,10 ґ
10-3, (0,16)]
10-3 = 2,10 ґ
10-3, |
|
| Db = 1,05 ґ 10-3, | |
-Dс = [-0,46 - 0,12 - 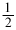 (-0,90)]
105 = -0,13 ґ 105, (-0,90)]
105 = -0,13 ґ 105, |
|
| Dс = 0,13 ґ 105. |
Подставив полученные численные значения коэффициентов в уравнение (9.13), найдем
| DH°реакции = DH°I - 3,07T + 1,05 ґ 10-3 T2 + 0,13 ґ 105T -1. | (9.14а) |
Константа интегрирования DH°I для этой реакции рассчитывается довольно просто. Рассмотрим нашу реакцию при 298,15° К; она выразится следующим уравнением:
| Н2 газ | + | 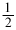 |
S2 газ | = | Н2Sгаз. |
| (идеальное состояние, 298°) |
(идеальное состояние, 298°) |
(идеальное состояние, 298°) |
Теплота реакции в этом случае определяется выражением
DH°реакции = DH°обр H2S
газ - DH°обр
H2 газ - 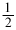 DH°обр S2 газ. DH°обр S2 газ. |
Необходимые значения теплоты образования (при 298° К) имеются в приложении 2. Итак,
DH°реакции = -4815 - 0 - 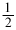 (29860) = -19745
кал/моль. (29860) = -19745
кал/моль. |
Подставив это значение в уравнение (9.14а) и воспользовавшись условием Т = 298°, получаем
| -19745 = DH°I - 3,07 (298) + 1,05 ґ 10-3 (298)2 + 0,13 ґ 105 (298)-1, |
откуда следует, что DH°I = -18 964 кал/моль.
Теперь для любой температуры Т уравнение (9.14а) примет вид
| DH°реакции = -18 964 - 3,07T + 1,05 ґ 10-3T 2 + 0,13 ґ 105T -1. | (9.15) |
Подставим в него интересующую нас температуру Т = 1000 и, проделав необходимые вычисления, найдем1 (стр.258)
| DH°реакции 1000 = -20981 кал/моль. | (9.16) |
Стандартную теплоту этой
реакции при 1000° К можно рассчитать и непосредственно по табличным данным
для H°1000 - H°298 и DH°реакции 298.
|
1 (стр.258) Здесь следует напомнить, что теплота образования соединения определяется теплотой, поглощенной при реакции образования этого соединения из элементов в их стандартном состоянии при любой данной температуре. При температуре 1000° К и выше пары серы, как мы уже отмечали, существуют преимущественно в виде молекул S2. Таким образом, если исследователю придется иметь дело с высокой температурой, то за стандартное состояние ему следует принять S2 газ. Тогда величина DH°реакции, рассчитанная нами, будет эквивалентна DH°обр Н2S, если исходными компонентами считать Н2 газ и S2 газ; в отличие от этого приводимая в таблицах величина DH°обр Н2S при 298,15° К отвечает образованию H2S из H2 газ и Sромбич. |
Чтобы показать, как это делается, рассмотрим общий случай - реакцию между веществами А и В с образованием соединения С. Предположим, что эта реакция протекает сначала при температуре T1, а потом при Т2; тогда для реакции
| А + В = С, | (9.17) |
| DH°реакции Т2 = H°C T2 - Н°А Т2 - Н°B Т2, | (9.18) |
| DH°реакции Т1 = Н°C T1 - Н°A T1 - Н°B T1. | (9.19) |
Вычтем уравнение (9.19) из уравнения (9.18):
| DH°реакции Т2 - DH°реакции Т1 = (H°T2 -H°T1)C - (H°T2 - H°T1)A - (H°T2 - H°T1)B. | (9.20) |
Для табличных данных, соответствующих начальной температуре 298,15° К, уравнение (9.20) примет следующий вид:
| DH°реакции Т = DH°реакции 298 + (H°T - H°298)C - (H°T - H°298)A - (H°T - H°298)B. | (9.21) |
Чтобы решить уравнение (9.21) применительно к реакции образования H2S при 1000° К, необходимо вспомнить, что мы уже рассчитали DH°реакции = -19 745 кал/моль при 298,15° К. Из той же работы Келли [6] найдем, что (H°1000 - H°298)H2S = 6695, (H°1000 - H°298)H2 = 4940 и 1/2 (H°1000 - H°298)S2 = 2988. Подставим эти значения в уравнение (9.21) и определим, что
| DH°реакции 1000 = -20987 кал/моль | (9.22) |
Полученная величина прекрасно соответствует значению DH°реакции 1000, найденному по уравнению (9.16). Это, конечно, вполне закономерно; хотя вычисления по уравнениям (9.22) и (9.16) и идут различными путями, но все они основаны на одних и тех же экспериментальных данных. Эти два метода мы подробно рассмотрели для того, чтобы показать возможность нескольких путей решения для одной задачи.
Уравнению (9.20) можно придать и более общий вид для любого числа реагентов и продуктов реакции:
| DH°реакции T2 - DH°реакции T2 = s(H°T2 - H°T1)продуктов реакции - s (H°T2 - H°T1)реагентов. | (9.23) |
Соответствующие уравнения теплоты образования соединения выводятся непосредственно из уравнения (9.23):
| DH°обр соед T2 - DH°обр соед T1 = (H°T2 - H°T1)соед - s(H°T2 - H°T1)элементов. | (9.23a) |
Э н т р о п и я. Если вещество в любом обратимом процессе при постоянной температуре Т поглощает теплоту из окружающей среды, то повышение его энтропии определяется количеством, поглощенной теплоты, деленным на абсолютную температуру:
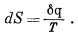 |
(9.24) |
Поскольку, согласно определению,
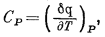 |
(9.25) |
уравнение (9.24) можно преобразовать:
| dS = (CP dT)/T (P постоянно). | (9.26) |
Частное интегрирование уравнения (9.26) дает
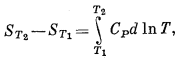 |
(9.27) |
или
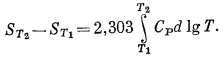 |
(9.28) |
Если СP не меняет свою величину в интересующем нас температурном интервале, то уравнение (9.28) сводится к выражению
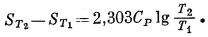 |
(9.29) |
Когда представляется возможность выразить СP в виде простого эмпирического уравнения вроде (9.7), то это эмпирическое уравнение может быть подставлено в уравнение (9.26); интегрирование последнего даст искомый результат (как это мы проделали для случая энтальпии). Обычно же уравнение (9.28) рассчитывается графически: строится график экспериментальных значений СP относительно lgТ и измеряется площадь ниже получившейся кривой. Эта площадь и равна (ST2 - ST1)/2,303. Величину энтропии при температуре T1 можно определять, считая энтропию при Т2 постоянной.
Огромное количество экспериментальных данных свидетельствует o том, что энтропия всех веществ при полном внутреннем равновесии равна нулю при 0°К. В этом заключается сущность третьего закона термодинамики, впервые в удовлетворительном виде сформулированного Льюисом и Рендаллом [10].
Поскольку считается, что энтропия любого хорошо кристаллизующегося чистого вещества при 0° К равна нулю, представляется возможным рассчитать и представить в форме таблиц абсолютные энтропии; сам по себе такой расчет несложен. Обратимся к уравнению (9.28) и приравняем T1 нулю; тогда, согласно третьему закону термодинамики, ST1 равно нулю, а для Т2 = 298 (если быть точным, то 298,15)
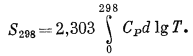 |
(9.30) |
Величину S298 можно вычислить, используя уже рассмотренные методы. Таблицы значений S298 проводятся в приложении 2.
Если стандартная энтропия образования всех элементов S°обр равна нулю при 0°К, то для других температур она будет величиной положительной. В отличие от энтропии DF°обр и DH°обр для элементов в их стандартном состоянии, как указывалось ранее, принято считать равными нулю при любой данной температуре.
Изменение стандартной энтропии реакции при температуре Т или DS°реакции T определяется выражением
| DS°реакции T = sS°Т продуктов реакции - sS°Т реагентов. | (9.31) |
Использование уравнения (9.31) покажем на примере реакции, рассматривавшейся нами ранее, а именно
|
(9.31a) |
Величина DS°реакции при 298,15° К определяется из уравнения (9.31), которое применительно к нашей реакции принимает вид
| DS°реакции =S°гиббсит - S°корунд - 3S°H2O. | (9.32) |
Найдем численные значения S° в приложении 2 и подставим их в уравнение (9.32):
| DS°реакции = 33,51 - 12,19 - 3(16,72), DS°реакции = -28,84 кал/моль. | (9.33) |
Итак, мы в состоянии решить нашу первейшую задачу, а именно получаем возможность использования величин энтропии, вычисленных в соответствии с третьим законом термодинамики, для расчета DF°реакции по уравнению (9.1):
| DF°реакции = DH°реакции - T DS°реакции |
Для только что рассмотренного примера гидратации корунда до гиббсита, как было установлено выше [по уравнению (9.3а)], DH°реакции = -9660 кал/моль; используя это значение, а также только что рассчитанную величину DS°реакции = -28,84 кал/моль, мы найдем
| DF°реакции = -9660 - 298(-28,84) = -1066 кал/моль, DF°реакции = -1,07 ккал/моль. | (9.34) |
Как уже указывалось выше, сведения по энтропии в таблицах обычно приводятся в виде разности ST - ST'. В работе Келли [6] даны значения S°T - S°298. Для всех тех веществ и температур, для которых даются и значения Н°T - H°298. Очень полезна также работа Келли и Кинга [7], в которой сведены имеющиеся значения энтропии для 298,15° К большинства элементов и их неорганических соединений.
Итак, абсолютные энтропии
сведены в таблицах в виде значений S°298, а для
различных температур - в виде значений S°T или в виде
разности S°T - S°T'. За
начальную температуру Т' обычно принимается температура 298,15° К.
Сведения по энтропии могут быть также представлены в виде эмпирической
температурной функции С°P.
Полезный и точный метод обобщения термодинамических данных и сведения их в виде таблиц - использование функции свободной энергии - (F°T - Н°T')/Т. Эту функцию отличает то достоинство, что она довольно медленно меняется с изменением температуры, а это допускает точную интерполяцию. Цифровые значения этой функции обычно даются для начальной температуры Т' = 0° К или 298,15° К. Таблицы таких значений имеются для значительного числа элементов и соединений [17; 11, стр. 669-686].
Использование функции свободной энергии рассмотрим на примере реакции
2CuOкрист + 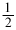 S2 газ =
Cu2Sкрист + O2 газ. S2 газ =
Cu2Sкрист + O2 газ. |
(9.35) |
для температуры 1000° К. Необходимые значения функции свободной энергии для всех веществ, участвующих в данной реакции, и для нескольких температур сведены в табл. 9.2.
Таблица. 9.2
| -(F° - Н°298)/Т, кал/градЧмоль | DH°обр
298, ккал/моль | ||||
| 298,15°К | 500° К | 1000°К | 1500°К | ||
| СuOкрист | 10,19 | 11,43 | 16,09 | 20,07 | -37,6 |
| S2 газ | 54,51 | 55,42 | 58,72 | 61,35 | 30,84 |
| Cu2Sкрист | 28,9 | 31,85 | 41,51 | 51,66 | -19,0 |
| O2 газ | 49,01 | 49,83 | 52,78 | 55,19 | 0 |
Согласно определению, изменение свободной энергии в процессе реакции равно сумме свободных энергий продуктов реакции минус сумма свободных энергий реагентов; сходным образом определяется энтальпия реакции. Следовательно, для любой реакции будет справедливо следующее выражение (основанное на H°298):
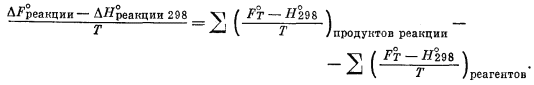 |
(9.36) |
В частности, для реакции (9.35)
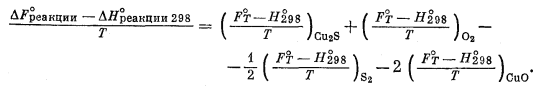 |
(9.37) |
Возьмем соответствующие числовые значения для 1000° из табл. 9.2 и подставим их в уравнение (9.37). Получим
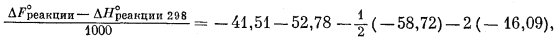 |
т. е.
| DF°реакции - DH°реакции 298 = -32,75 ккал/моль. | (9.38) |
Величину DH°реакции 298 нетрудно рассчитать, исходя из теплот образования DH°обр 298, значения которых также имеются в табл. 9.2. Определяем, что DH°реакции 298 = 40,8 ккал/моль. Подставляем полученный результат в уравнение (9.38) и находим, что
| DF°реакции 1000° = 8,0 ккал/моль. | (9.39) |
Кроме того, поскольку
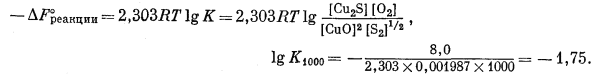 |
Активности твердых веществ при 1 атм общего давления равны единице, поэтому мы вправе написать
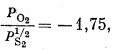 |
или
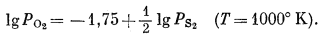 |
(9.40) |
На основании серии подобных вычислений можно рассчитать диаграмму парциальных давлений для 1000° К (или для любой другой повышенной температуры) - диаграмму такого же типа, которые были нами рассмотрены в гл. 6 для 298,15° К (25° С).
Как мы уже указывали, Келли удалось свести в таблицы термодинамические данные для большого числа соединений и элементов. В одной из его работ [6] собраны сведения относительно Н°T - Н°298 и S°T - S°298, а в другой [7] - для S°298. По его данным можно без особого труда рассчитать функцию свободной энергии: это мы покажем ниже.
Согласно определению,
| F°T = Н°T - TS°T. | (9.41) |
Из обеих частей уравнения (9.41) вычтем Н°298 и разделим обе части на Т:
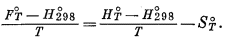 |
(9.42) |
К правой части уравнения (9.42) одновременно прибавим S°298 и -S°298:
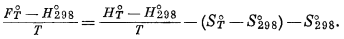 |
(9.43) |
Полученное выражение принимает удобную для нас форму.
Согласно определению, свободная энергия образования соединения определяется изменением свободной энергии в процессе реакции образования этого соединения из входящих в его состав элементов в их стандартном состоянии. Следовательно, с помощью функций свободной энергии соединения и элементов мы можем вычислить свободную энергию образования этого соединения для любой интересующей нас температуры. Уравнение DF°обр T можно вывести непосредственно из уравнения (9.36):
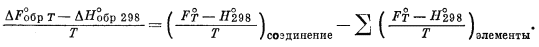 |
(9.44) |
Для примера рассчитаем DF°обр корунда Аl2О3 при 500° К. Соответствующая реакция может быть выражена следующим уравнением:
2Alкрист + 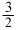 O2 газ =
Al2O3 крист. O2 газ =
Al2O3 крист. |
Уравнение (9.44) в этом случае примет вид
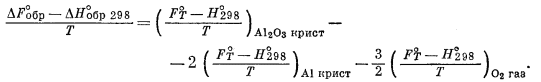 |
(9.45) |
Подберем необходимые значения функции свободной энергии (при 500° К) из книги Льюиса и Рендалла [11, приложение 7] и получим
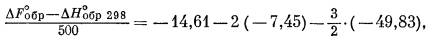 |
|
| DF°обр = DH°обр 298 + 37518 кал/моль. |
Величина DH°обр 298 для корунда приведена
в приложении 2; она составляет -399,09 ккал/моль. Тогда| DF°обр корунда 500 = -361,57 ккал/моль. |
Сравним полученный результат с величиной свободной
энергии образования при комнатной температуре, т. е. при 298° К; эта
величина равна -376,77 ккал/моль. Таким образом, повышение
температуры от 25 до 227° С приводит к увеличению свободной энергии
соединения примерно на 4%.
Для дальнейшего изложения было бы удобно, если бы мы сейчас попытались определить наклон кривой, которая получается при нанесении значений DF°реакции на график в зависимости от Т. Согласно ранее приведенному уравнению (9.1),
| DF°реакции = DH°реакции - T DS°реакции. |
Это уравнение относится только к стандартным условиям. Однако оно в общем остается в силе и для любых давлений, но тогда его следует переписать:
| DFреакции = DHреакции - T DSреакции. | (9.46) |
Далее продифференцируем это уравнение относительно температуры при условии постоянного давления:
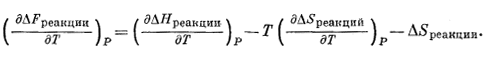 |
(9.47) |
Однако поскольку по уравнению (9.26)
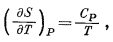 |
то для реакции
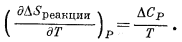 |
(9.48) |
Кроме того, согласно уравнению (9.9),
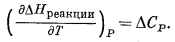 |
Подставим эти результаты в уравнение (9.47) и получим
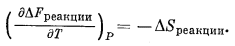 |
(9.49) |
В частном случае для стандартных условий
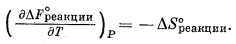 |
(9.50) |
Это и есть искомый
результат. Если величину стандартного изменения свободной энергии реакции
нанести на график в зависимости от абсолютной температуры, то наклон
кривой при каждой температуре будет определяться отрицательным значением
стандартного изменения энтропии реакции.
При обсуждении вопроса об изменении свободной энергии реакций в зависимости от температуры полезно рассмотреть несколько типов химических реакций, временно исключив реакции с участием фаз переменного состава. Итак, рассмотрим следующие типы реакций: 1) реакции только между твердыми веществами; 2) реакции между твердыми веществами и жидкостями или только между жидкостями (или же между жидкостями в их надкритическом состоянии); 3) реакции только между газами или для любой комбинации твердых веществ, жидкостей и газов. Прежде всего обратимся к реакциям первого типа.
Р е а к ц и и м е ж д у т в е р д ы м и в е щ е с т в а м и. Помимо обычной теплоемкости СP, которая относится к 1 моль, введем понятие о грамм-атомной теплоемкости СP, величина которой определяется мольной теплоемкостью вещества, деленной на число атомов в его молекуле. Так, например, для силлиманита Al2SiO5 СP = СP/8.
При повышенных температурах грамм-атомная теплоемкость почти всех кристаллических веществ, будучи измеренной при постоянном объеме, достигает теоретической величины 3R = 5,96 кал/град. Для твердых веществ такие теплоемкости при постоянном объеме СV и при постоянном давлении СP почти не отличаются одна от другой. Томпсон [22] показал, что грамм-атомная теплоемкость большинства породообразующих минералов близка к 3R в интервале температур от 600 до 1000° С.
Фактическое постоянство грамм-атомных теплоемкостей означает, что DСP для реакций с участием только твердых веществ будет близко к нулю. Докажем этот вывод на примере реакции образования силлиманита при высокой температуре из входящих в его состав окислов:
|
|||||||||||||||||||||
Вспомним, что для любой реакции, согласно уравнению (9.48),
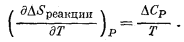 |
Кроме того, по уравнению (9.9)
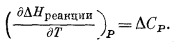 |
Уравнения (9.9) и (9.48) свидетельствуют о том, что при небольшом значении DСP изменение DHреакции и DSреакции с изменением температуры также будет очень небольшим. Далее, Томпсон [22] показал, что для большинства реакций между твердыми веществами, представляющими геологический интерес, отношение (DСP)/Т меньше 1,2 ґ 10-3 кал/мольЧград2. По-видимому, эта оценка справедлива до температур порядка 1000° К или еще более высоких.
Во всяком случае для температуры выше 25° С в первом приближении можно допустить, что для реакций между твердыми веществами DS°реакции и DH°реакции постоянны. Если это так, то на основании уравнения (9.1) мы можем написать
| DF°реакции T = DH°реакции 298 - TDS°реакции 298. | (9.51) |
Уравнение (9.51) позволяет рассчитать приближенное значение DF°реакции при несколько более высокой температуре, исходя из обычных данных по величине теплосодержания и энтропии образования, относящихся к 298°К.
Таблица 9.3
| Минерал | Формула | DH°обр, ккал/моль | Мольная энтропия, кал/град |
Грамм-атомная энтропия, кал/град | |
| Гиббсит | А1(ОН)3 | -306,8±?1 (стр.266) | 16,8±0,12 (стр.266) | 2,400±0,014 | |
| Корунд | Al2O3 | -400,4±0,3 | 12,17±0,02 | 2,434±0,004 | |
| Кианит | Al2(SiO4)O | - | 20,02±0,08 | 2,502±0,010 | |
| Андалузит | AlAl(SiO4)O | -642,2±?1 (стр.266) | 22,28±0,10 | 2,785±0,012 | |
| Силлиманит | Al2SiO5 | -648,9±?1 (стр.266) | 22,97±0,10 | 2,871±0,012 | |
| Брусит | Mg(OH)2 | -221,9±0,5 | 15,09±0,05 | 3,02±0,01 | |
| Жадеит | NaAl(Si2O6) | - | 31,9±0,3 | 3,19±0,03 | |
| Клиноэнстатит | Mg(SiO3) | -362,7±0,7 | 16,22±0,10 | 3,24±0,02 | |
| Форстерит | Mg2(SiO4) | -512,9±1,0 | 22,75±0,20 | 3,25±0,03 | |
| Периклаз | MgO | -143,80±0,09 | 6,50±0,15 | 3,25±0,075 | |
| Кварц (низкотем- пературный) |
SiO2 | -210,2±0,4 | 9,88±0,01 | 3,293±0,003 | |
| Кристобалит (низ- котемпературный) |
SiO2 | -209,45±0,25 | 10,38±0,01 | 3,460±0,003 | |
| Тридимит (низко- температурный) |
SiO2 | -209,42±0,4 | 10,50±0,10 | 3,500±0,033 | |
| Портландит | Ca(OH)2 | -235,8±?1 (стр.266) | 17,4±1,02 (стр.266) | 3,5±0,3 | |
| Альбит | Na(AlSi3O8) | - | 50,2±0,4 | 3,86±0,03 | |
| Волластонит | CaSiO3 | -383,2±0,6 | 19,6±0,2 | 3,92±0,04 | |
| Нефелин | NaAlSiO4 | - | 29,1±0,22 | 4,16±0,03 | |
| Арагонит | СаСО3 | -288,5±?1 (стр.266) | 21,2±0,32 | 4,24±0,06 | |
| Кальцит | СаСО3 | -288,3±0,35 | 22,2±0,2 | 4,44±0,04 | |
| Известь | CaO | -151,8±0,3 | 9,5±0,2 | 4,75±0,10 | |
| Вода (жидк.) | H2O | -68,32±0,01 | 16,75±0,03 | 5,58±0,01 | |
| |||||
В табл. 9.3 для температуры 25° С приведен ряд значений мольной энтропии, грамм-атомной энтропии и теплоты образования некоторых минералов, представляющих большой интерес для геологов. Данные таблицы показывают, что при 25° С и 1 атм давления величины грамм-атомной энтропии находятся в узких пределах - от 2,4 до 4,8 кал/град (исключение составляет жидкое вещество - вода). Столь небольшой разброс величин грамм-атомной энтропии означает, что изменение мольной энтропии любой реакции с участием этих соединений также будет небольшим, поскольку общее число атомов в процессе реакции остается постоянным. Например, для случая образования клиноэнстатита из периклаза и кварца при 25° С мы имеем
|
(9.52) | |||||||||||||||||||||||||
Отметим две особенности полученных данных: во-первых, величина DS°реакции очень мала, во-вторых, ошибка определения DS°реакции составляет примерно 50%. Вычисляя DH°реакции 298. Для реакции (9.52), по соответствующим значениям DH°обр из табл. 9.3 находим, что DH°реакции 298 = 8700 ± 1190 кал/моль. Подставив эти два значения (вместе с присущими им экспериментальными ошибками) в уравнение (9.51), найдем что для Т = 700° К
| DF°реакции 700 = DH°реакции 298 - 700DS°реакции 298, | (9.53) |
| DF°реакции 700 = -8700 ± 1190 - 700(-0,18 ± 0,1), | (9.53a) |
| DF°реакции 700 = -8700 ± 1190 + 126 ± 70, | (9.53б) |
| DF°реакции 700 = -8574 ± 1260 кал/моль. | (9.53в) |
В общей величине DF°реакции 700 на долю TDS°реакции приходится примерно одна десятая ошибки, связанной с определением DH°реакции. Таким образом, в случае данной частной реакции при расчетах с любыми практическими целями мы вправе исходить из предположения о равенстве DF°реакции T = DH°реакции 298 либо вести вычисления по уравнению (9.53).
При дальнейшем рассмотрении нашего примера мы еще раз проведем расчет величины DF°реакции 700 также без каких-либо упрощений. Исходя из уравнения (9.43), для реакции образования соединения из входящих в его состав окислов мы можем написать
| DF°реакции
T = DH°реакции
298 - TDS°298 +
[(H°T -
H°298)соед - - S(H°T - H°298)окислы] - Т[(S°T - S°298)соед - S(S°T - S°298)окислы]. |
(9.54) |
Можно считать, что уравнение (9.54) состоит из уравнения (9.51) плюс введенные поправки. Величину этих дополнительных членов можно найти в работе Роби [17]; воспользуемся ими, равно как и результатом вычисления по уравнению (9.53в), и найдем
| DF°реакции 700 = -8574 + [9600 - 5630 - 4100] - 700 [19,95 - 11,62 - 8,60], | |
| DF°реакции 700 = - 8574 - 130 + 189 = - 8574 + 59, | |
| DF°реакции 700 = -8515 ± 1260 кал/моль. | (9.55) |
(Предполагается, что в связи с введением в уравнение значений H°700 - H°298 и S°700 - S°298 погрешности не возрастают.)
Полученный результат показывает, что величина поправок составила всего 59 кал, т. е. оказалась значительно меньшей, чем ошибка, связанная с неточностью определения стандартных энтальпий образования и энтропий. Итак, в конце концов, для реакции (9.52) при 700° К мы получили следующие результаты:
| DF°реакции = -8,7 ± 1,3 (при предположении, что DS°реакции = 0 |
и что DF°реакции
700 = DH°реакции
298);
DF°реакции =
-8,6 ± 1,3 [пользуясь уравнением (9.51)];
DF°реакции = -8,5 ± 1,3 [(без
каких-либо упрощений, по уравнению (9.1)].
Здесь все величины даны в килокалориях на моль и округлены до десятой доли килокалории на моль.
Таким образом, для частной рассмотренной реакции, а именно для реакции образования клиноэнстатита из периклаза и кварца, экспериментальная ошибка, присущая численной величине DF°реакции, значительно превышает ошибки, вызванные различными допущениями. И вообще экспериментальная ошибка, связанная с величиной DF°реакции, Для реакций между твердыми веществами в процентном отношении должна быть довольно высокой, что видно уже из табл. 9.3. Этот момент всегда следует иметь в виду при любых попытках использовать результаты подобных вычислений для решения геологических проблем.
Р е а к ц и и с у ч а с т и е м ж и д к о с т е й. По своей теплоемкости чистые жидкости существенно не отличаются от соответствующих им твердых веществ. Как и для реакций между твердыми веществами, величина DСP для реакций с участием твердых веществ и жидкостей или только жидкостей будет небольшой и почти не будет меняться с изменением температуры. В результате изменение DF°реакции с температурой окажется столь же небольшим, как и в случае реакций между твердыми веществами.
Р е а к ц и
и с у ч а с т и е м г а
з о в. Если реакция протекает с участием газа, то
величина DСP может
оказаться большой. В этом случае мы не имеем права сразу же прибегнуть к
упрощениям, что возможно для реакций с участием жидкостей и твердых
веществ. Однако, как мы покажем уже в следующем разделе, возможность
систематического подхода к решению данной проблемы имеется и в этом
случае.
Уравнение (9.50) говорит нам о следующем: если на графике откладывать значения DF°реакции относительно температуры, то наклон получающейся кривой будет определяться величиной - DS°реакции T. Как мы показали для реакций между твердыми веществами и реакций с участием жидкостей, уравнение (9.51) справедливо лишь в первом приближении: если бы мы построили график зависимости DF°реакции T от температуры, то получили бы прямую линию с наклоном - DS°реакции 298.
Однако оказывается, что подобные прямолинейные соотношения достаточно близко соответствуют реакциям всех типов. Этот вывод означает, что любую реакцию можно описать эмпирическим уравнением типа
| DF°реакции T = А - ВT, | (9.56) |
где А и В - константы для каждой данной реакции. Чтобы понять уравнение (9.56), сравним его с уравнением (9.1), а именно
| DF°реакции T = DH°реакции T - TDSреакции T . |
Подобное упрощение оправдывается следующими двумя соображениями. Во-первых, величины DS°реакции и DH°реакции не обнаруживают значительных изменений с температурой, за исключением случаев фазовых превращений (что будет рассмотрено ниже). Во-вторых, изменения величин DH°реакции и DS°реакции, связанные с изменением теплоемкости реагирующих веществ в зависимости от температуры, как бы компенсируют друг друга. Поэтому степень изменения DF°реакции не зависит от температуры и остается величиной постоянной.
Практически при наличии достаточно точных термодинамических данных величина DF°реакции T рассчитывается для некоторых температур с помощью методов, основанных на уравнении (9.1), а через полученные точки на диаграмме проводится отличная прямая линия.
Ричардсон и его сотрудники в серии интересных статей [14-16] привели несколько графиков с подобными прямолинейными соотношениями для некоторых типов реакций, представляющих определенный интерес для геохимиков.
В своих первых работах Ричардсон с сотрудниками приводили и аналитические выражения, и графические построения примерно для 90 с лишним реакций, сопровождая их многочисленными замечаниями по существу расчетов. На фиг. 9.1 и 9.2 мы воспроизводим немногие из полученных ими результатов для реакций разных типов.
На фиг. 9.1 в основном нашли свое отражение реакции между твердыми веществами. В общем точность нанесения каждой реакции на график, указанная в подписях, зависит от оценки точности имеющихся термодинамических данных, а не от каких-либо отклонений от прямолинейности. Эта фигура показывает, что, за исключением реакций образования бората, наклон линий действительно совсем небольшой.
С повышением температуры могут происходить различные фазовые превращения. Твердое вещество может испытывать полиморфные превращения или расплавляться до жидкого состояния; наконец, оно может возгоняться до газообразного состояния, а жидкость может вскипать. Подобные фазовые превращения происходят скачкообразно, т. е. в чрезвычайно узких температурных интервалах. Все подобные изменения состояния вещества сопровождаются поглощением тепла, за исключением полиморфных превращений, когда теплота может либо выделяться, либо поглощаться в зависимости от частных особенностей процесса превращения1 (стр.269). Согласно определению, изменение теплосодержания вещества, испытывающего (изотермическое) превращение при постоянном давлении, попросту говоря, равно количеству поглощенного тепла. Сходным образом, изменение энтропии равно количеству поглощенного (выделенного) тепла, деленному на абсолютную температуру. Следовательно, после того как рассматриваемое вещество испытает фазовое превращение, величины DH°обр T и DS°обр T обычно становятся иными, чем они были до превращения. Это в свою очередь скажется На величине новых DH°реакции T и DS°реакции T; наклон линии DF°реакции T на графике относительно температуры, как правило, также будет иным, но останется по-прежнему постоянным.
Такое изменение наклона линии DF°реакции T хорошо заметно для реакции СаО + 2В2О3 = CaB4O7 (фиг. 9.1). Вплоть до температуры 450° С эта реакция идет между двумя твердыми кристаллическими веществами. При указанной температуре В2О3 расплавляется, и теперь уже реакция происходит между твердым веществом и жидкостью. При 987° С расплавляется продукт реакции СаВ4O7 и наклон линии вновь меняется, становясь отрицательным, но не таким крутым, как прежде.
Все реакции, рассмотренные
на фиг. 9.1, касаются только твердых и жидких веществ при давлении 1
атм. Активности всех этих веществ равны единице; следовательно,
если величина DF°реакции
T отрицательна, то
|
1 (стр.269) Теплота, поглощаемая в процессе расплавления вещества, называется (скрытой) теплотой плавления; теплота, идущая на кипение, называется (скрытой) теплотой парообразования; теплота, затраченная в процессе возгонки, называется (скрытой) теплотой сублимации. |
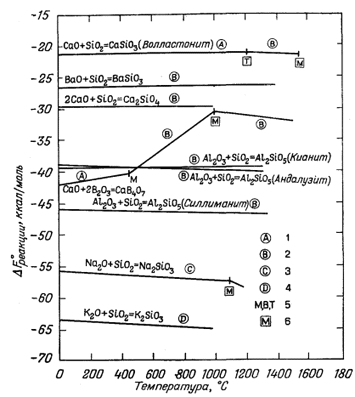 |
| Фиг. 9.1. Стандартные свободные энергии реакции как функция
температуры (в градусах Цельсия) для серии реакций между
окислами. Буквенные обозначения на этой фигуре и на фиг. 9.2: 1 - оцениваемая точность ±1 ккал; 2 - оцениваемая точность ±3 ккал; 3 - оцениваемая точность ±10 ккал; 4 - оцениваемая точность > ±10 ккал; 5 - плавление, кипение и фазовый переход реагента; 6 - плавление и т. д. продукта реакции [15]. |
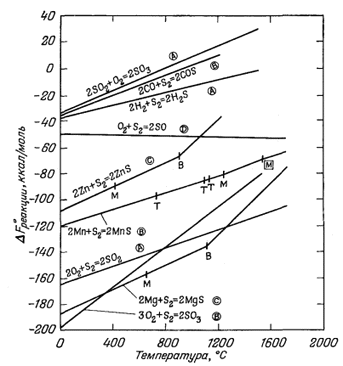 |
| Фиг. 9.2. Стандартные свободные энергии реакции как функция температуры (в градусах Цельсия) для различных реакций, в которых участвует газообразная сера S2 [16]. |
в любом случае это будет означать, что участвующие в реакции окислы неустойчивы по отношению к образующемуся продукту реакции при всех рассматриваемых температурах. Такой вывод следует из уравнения (1.13), согласно которому
| DFреакции Т = DFреакции + RТ ln Q. |
Поскольку для данного типа реакций Q = 1, то DF°реакции T = DF°реакции T. Эта реакция будет равновесной лишь при условии, что DFреакции T = DF°реакции T = 0, т. е. в том случае, если линия данной реакции будет наклонена столь круто, что пересечет (абсциссу) нулевое значение DF°реакции T; ни одна из линий на нашей диаграмме не удовлетворяет этому условию.
Рассматривая равновесные условия для подобных реакций, следует помнить, что в этом отношении мы связаны двумя ограничениями. Во-первых, принято, что давление равно 1 атм и, во-вторых, что мы имеем дело лишь с чистыми фазами. Однако в общем случае давление может варьировать, а в реакциях могут принимать участие твердые и жидкие растворы, так что активности компонентов в этих фазах также будут переменными.
Весьма показательны линии DF°реакции T для реакций образования двух полиморфных фаз - кианита и андалузита. На фиг. 9.1 видно, что эти линии пересекаются при температуре примерно 500° С. Точка пересечения как раз и дает ту температуру, при которой обе полиморфные модификации обладают одинаковой величиной свободной энергии (при 1 атм); именно эта температура для них и является равновесной. Точность установления температуры (полиморфного превращения) с помощью графиков подобного рода довольно низка, что можно видеть по небольшому наклону этих двух линий, а также по тому, что само положение линий установлено с точностью ±3 ккал. Как правило, температуры полиморфных превращений получают более точными методами, непосредственно по данным изучения равновесии в зависимости от давления и температуры.
На фиг. 9.2 показаны некоторые линии DF°реакции T в зависимости от температуры для реакций между газами и между газами и твердыми веществами. Понятно, что в каждом из рассматриваемых случаев сере приписывается газообразное состояние в виде молекул S2. Тут же следует отметить, что линии реакций отличаются бо,лее крутым наклоном, чем на фиг. 9.1, за исключением реакции образования SO. Для всех учтенных здесь реакций активности твердых и жидких веществ равны единице, но активности газов могут меняться. Эти реакции равновесны при условии, что
| DF°реакции T = - RT ln K. |
Например, для реакции 2Znкрист + S2 гaз = 2ZnSкрист мы имеем
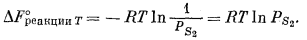 |
При построении диаграммы фиг. 9.2 использованы данные, заимствованные из статьи Ричардсона и Джефса по сульфидам [16], в которой приводятся графики для большого числа реакций между металлами и газообразной серой. В другой своей статье Ричардсон и Джефс [14] решили подобную проблему в отношении реакций между металлами и газообразным кислородом. В последней работе для каждой рассматриваемой реакции выведено выражение, построенное по типу
| DF°реакции T = RT lnРO2. |
Основываясь на использовании термохимических данных, аналогичных рассматриваемым в настоящей главе, Холланд [5] построил ряд диаграмм устойчивости для обычных металлов рудных месторождений. На его диаграммах поля устойчивости различных соединений даются в виде функций фугитивности серы или кислорода, а также температуры. Напомним, что при низких и умеренных давлениях фугитивность газа численно равна его парциальному давлению.
Построение диаграммы парциальных давлений как функции температуры производится таким же образом, как и для постоянной температуры
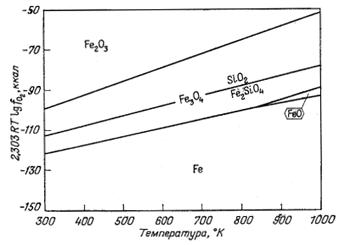 |
| Фиг. 9.3. Диаграмма устойчивости окислов железа, у которой в качестве характеристических переменных приняты температура и 2,303 RT lg fO2 [5, стр. 187]. |
25° С, что было рассмотрено в гл. 6; теперь лишь устойчивые соотношения нужно вычислять для каждой интересующей нас температуры. На диаграмме (фиг. 9.3), заимствованной из работы Холланда, показана устойчивость окислов железа. На эту же диаграмму наложена линия равновесия между Fe2SiO4 и SiO21 (стр.272).
Поскольку каждая из реакций, изображенных на фиг. 9.3, относится к одному и тому же типу, т. е. все они подобны реакции
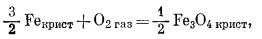 |
то свободная энергия каждой реакции определяется выражением типа
| DF°реакции Т = RT ln РO2 . |
Как мы уже показали ранее (на примере фиг. 9.2 для реакций с участием S2 гaз), значения DF°реакции Т на графике относительно Т образуют прямую линию, определяемую функцией А - ВТ. Следовательно,
| DF°реакции Т = А + ВТ = 2,303 RT lg fO2. |
|
1 (стр.272) Точнее, линия равновесия между Fe3O4, Fe2SiO4 и SiO2, согласно реакции 3Fe2SiO4 + О2 газ = 2Fe3O4 + 3SiO2.- Прим. ред. |
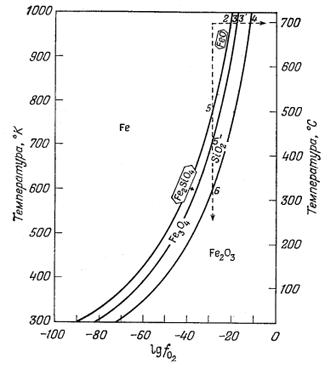 |
| Фиг. 9.4. Диаграмма, изображающая устойчивость окислов железа в зависимости от температуры и lg fO2 как определяющих переменных [5]. |
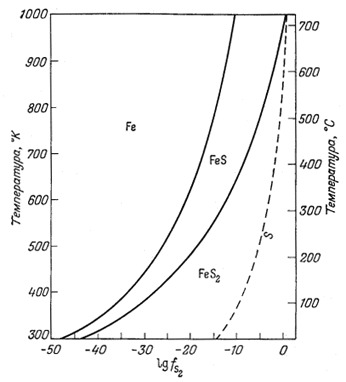 |
| Фиг. 9.5. Диаграмма устойчивости сульфидов железа, у которой характеристическими переменными служат температура и lg fS2 [5, стр. 189]. |
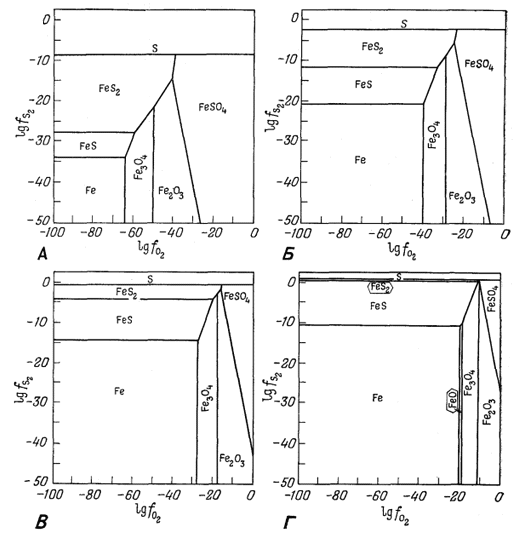 |
| Фиг. 9.6. Изотермические сечения диаграммы lg fO2 - lg fS2 - Т при (А) 400° К, (Б) 600° К, (В) 800° К, (Г) 1000° К [5]. |
Поэтому на фиг. 9.3 при соответствующем выборе ординат границы полей устойчивости определяются прямыми линиями. Та же диаграмма, но в более удобном виде, представлена на фиг. 9.4.
На фиг. 9.5 приведена
диаграмма, отражающая зависимость фугитивности серы от температуры для
сульфидов железа. Фиг. 9.6 представляет собой результат комбинации фиг.
9.4 и 9.5 в виде четырех изотермических сечений фугитивность -
фугитивность для температур 400, 600, 800 и 1000°К.
Термодинамические свойства электролитов при повышенных температурах (в том плане, как они были изложены в настоящей главе для фаз постоянного состава), по существу, все еще систематически не исследованы и не обобщены. Имеющиеся данные относительно свободной энергии образования, энтальпии образования и энтропии для ионов в водных растворах как функции температуры разбросаны в отдельных работах.
В гл. 4 мы изложили некоторые сведения о влиянии температуры на комплексообразование в водном растворе, в гл. 10 будут рассмотрены диаграммы устойчивости силикатных систем с участием ионных частиц при повышенных температурах.
Не исключено, что
обстоятельное обобщение свойств растворов электролитов будет сделано в
самом скором будущем. Порукой тому могут служить недавно опубликованные
работы Коббла [2] и Крисса [З]. К решению этой важной проблемы приступили
также и другие исследователи.
В настоящем разделе рассмотрен вопрос о расчете DF°реакции или DFреакции для всех интересующих нас температур. Дано определение таких термодинамических функций, как энтальпия, или теплосодержание, и энтропия, а также приведены уравнения, связывающие эти величины с теплоемкостью и температурой. Основу для исследования характера изменения DFреакции с температурой для различного типа реакций создают следующие два уравнения: для стандартных условий
| DF°реакции = DH°реакции - T DS°реакции | (9.1) |
и для любых давлений
| DFреакции = DHреакции - TDSреакции. | (9.46) |
Было показано, что для большинства реакций график
зависимости DF°реакции от
температуры представляет собой прямую, причем для конденсированных систем
такие линии обычно характеризуются малым наклоном. Рассмотрены различные
методы обобщения данных, характеризующих теплосодержание, теплоемкость,
энтропию и свободную энергию, а также функцию свободной энергии
-(F°T - H°T')/Т.
На ряде примеров показана возможность использования выведенных уравнений
для решения практических задач. Влияние изменения температурных условий на
устойчивые соотношения минералов проиллюстрировано несколькими диаграммами
парциального давления при повышенных температурах.
Ключевое соотношение, позволяющее оценить влияние изменения давления на изменение свободной энергии, определяется уравнением
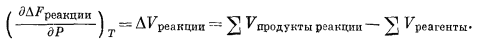 |
(9.57) |
Согласно уравнению (9.57), при постоянной температуре скорость изменения свободной энергии реакции (при любых заданных давлении и температуре) равна сумме мольных объемов продуктов реакции минус сумма мольных объемов реагентов.
Например, при 25° С и 1 для реакции
|
(9.58) | ||||||||||||||||||||
Следовательно,
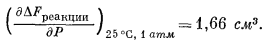 |
(9.59) |
В уравнении (9.59) объем выражен в кубических сантиметрах; если при этом давление дано в атмосферах, то DFреакции будет выражено в системе единиц кубический сантиметр - атмосфера. Эта последняя единица измерения энергии 1 cм3Чamм равна 0,02422 кал. Из уравнения (9.59) видно, что увеличение DFреакции при увеличении давления на 1 атм для 25° С (для давлений около 1 атм или пока DVреакции постоянно) определяется такой величиной:
| D (DFреакции) = 1,66 ґ 1 ґ 0,02422 = 0,0402 кал/мольЧатм. |
Величина DVреакции отражает влияние изменения давления на DFреакции т. е. играет ту же роль, что и величина - DSреакции характеризующая влияние температуры на изменение DFреакции. Многие рассуждения о величине и постоянстве DSреакции справедливы и в отношении DVреакции.
Объем твердых веществ в связи с изменением температуры и давления меняется незначительно1 (стр.276). При 25° С и 1 атм объемное расширение а для большинства породообразующих минералов определяется выражением
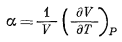 |
(9.60) |
и колеблется в пределах от 1 ґ 10-5 до 4 ґ 10-6 на 1 град. Сходным образом определяется изотермическая сжимаемость b:
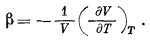 |
(9.61) |
Ее величина колеблется в пределах от 0,5 ґ 10-6 до 3 ґ 10-6 на 1 атм. Значения a и b несколько увеличиваются с повышением температуры и немного уменьшаются с увеличением давления.
Главное заключается в том, что, поскольку большая часть твердых веществ характеризуется примерно одинаковыми значениями термального расширения и сжимаемости, величина DVреакции в общем не изменяется для широкого диапазона колебаний температуры и давления. Итак, любое увеличение или уменьшение объема реагентов будет сопровождаться соответствующим увеличением или уменьшением объема продуктов реакции. Ниже будет приведен пример использования уравнения (9.57) для такой реакции, значение DVреакции которой постоянно2 (стр.276).
Ромбическая и моноклинная модификации серы равновесны при 368,5° К и 1 атм давления. Это условие выражается уравнением
| Sромбич = Sмонокл, DF°реакции 368,5 = 0. |
При температурах, превышающих 100° С, и при высоких давлениях
| Vмонокл - Vромбич = DVреакции = 0,4 см3. |
Предположим, что DVреакции постоянно, по крайней мере
в пределах точности имеющихся в нашем распоряжении численных величин.
|
1 (стр.276) Последующее изложение приведет к выводу о практическом постоянстве DVреакции для многих реакций; оно построено на основании работы Томпсона [22]. 2 (стр.276) Приводимый ниже материал основан на данных работы Льюиса и Рендалла (11, стр. 167, 169-170). |
На основании уравнения (9.57) имеем
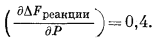 |
После интегрирования находим, что
| DFреакции PT - DFреакции P'T = 0,4(Р - Р'). |
Теперь приравняем Р' единице; тогда
| DFреакции PT - DF°реакции T = 0,4(Р - 1). |
В равновесных условиях при новом значении Р
| DFреакции PT = 0. |
Следовательно,
| -DF°реакции T = 0,4(Р - 1). | (9.61a) |
Уравнение (9.61а) связывает равновесное давление Р со стандартной свободной энергией реакции при любой температуре Т (согласно нашему выбору Т > 373° К). Рассчитаем теперь величину Р для Т = 380° К. Для этого нам необходимо знать величину DF°реакции 380.
Значения S°T для обеих модификаций серы приведены в работе Льюиса и Рендалла [11, стр. 167]. Для 368,5° К они составляют S°монокл = 9,07, S°ромбич = 8,81; следовательно, DS°реакции 368,5 = 0,26 кал/мольЧград. По уравнению (9.50)
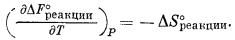 |
Поскольку мы исходим из предположения, что в небольшом температурном интервале DS°реакции есть величина постоянная, то интегрирование этого выражения (с соответствующей подстановкой численных значений) дает
| DF°реакции 380 = DF°реакции 368,5 = -0,26(380 - 368,5). |
Так как моноклинная сера равновесна с ромбической при 368,5° К и 1 атм, то DF°реакции 368,5 = 0. Отсюда следует, что
| DF°реакции 380 = -0,26 ґ 11,5 = -3,0 кал/моль. |
Теперь мы получили данные, необходимые для вычисления равновесного давления по уравнению (9.61а). Однако прежде всего следует перевести величину DF°реакции в размерность кубический сантиметр - атмосфера. Вспомним, что 1 см3Чатм = 0,02422 кал; отсюда 1 кал = 41,29 см3Чатм. Подставив этот коэффициент в уравнение (9.61а), получим
| -(-3,0) ґ 41,29 = 0,4 (Р - 1), P = 310 атм. |
Итак, резюмируем: две рассмотренные полиморфные модификации серы равновесны при 368,5° К и 1 атм, а также при 380° К и приблизительно 310 атм. Последняя величина точна в той степени, в какой точна входящая в наши расчеты величина DVреакции.
Мольные объемы при
температуре, близкой к комнатной, определяются без особого труда по
удельным весам, а при повышенных температурах - по дифракции рентгеновских
лучей. Современная сводка точных величин мольных объемов
имеется в работе Роби и Бетке [18 ]. Большая часть этих величин относится
к температурам, близким к 25° С. Значения плотности вместе с величинами а
и (3 приведены в справочнике Берча с соавторами [1].
Хорошим примером определения зависимости мольного объема от температуры может служить исследование Скиннера с соавторами [20], проведенное на полиморфных минералах состава Аl2SiO5 - андалузите, кианите и силлиманите. Было найдено, в частности, что величина V(см3/моль) для андалузита при 0° С равна 51,525, а при 100° С она составляет 51,624, т. е. превышает первую приблизительно на 0,2%. При 1000° С значение V достигает 53,405, т. е. увеличивается примерно на 4% по сравнению со значением для 100° С. Степень изменения мольного объема с температурой для силлиманита и кианита примерно одинакова и чуть меньше, чем для андалузита.
Жидкости и жидкообразные надкритические флюиды несколько напоминают твердые вещества в том отношении, что для них характерно низкое термическое расширение и сжимаемость. Для самой важной жидкости - воды зависимость объема от температуры и давления выведена Кеннеди [8].
Газы отличаются очень большими мольными объемами, а поэтому для реакций с участием газа величина DVреакции может оказаться огромной. Термальное расширение и сжимаемость газов при низких давлениях весьма высоки. С повышением давления газ по своим свойствам все более приближается к жидкости.
К сожалению, в настоящее
время отсутствует систематическая сводка величин мольного объема для
различных температур и давлений, подобная сводке по термальным свойствам,
опубликованной Келли с сотрудниками в серии бюллетеней "Bureau of Mines".
Если такие величины и имеются, то они разбросаны в обширной химической
литературе.
Характер изменения DFреакции в зависимости от давления при постоянной температуре рассмотрим на примере системы с участием жидкой воды, для чего воспользуемся результатами исследований Йодера и Уира [23].
Йодер и Уир занимались определением изменения объема и свободной энергии в зависимости от давления для реакций с участием кварца, воды, альбита (NaAlSi3O8), анальцима (NaAlSi2O6ЧH2O), нефелина (NaAlSiO4) и жадеита (NaAlSi2O6). Для реакции
| 2 анальцим = нефелин + альбит + 2 вода | (9.62) |
| DVреакции = VNe + VAB + 2VW - 2VAn. |
Зависимость мольных объемов (в кубических сантиметрах) от давления при 25° С определяется следующими выражениями:
| VNE = 54,120 - 1,113 ґ 10-4p + 0,28 ґ 10-9p2, | |
| VAb = 100,399 - 2,123 ґ 10-4p + 2,17 ґ 10-9p2, | |
| VW = 18,016 - 4,463 ґ 10-4p + 14,51 ґ 10-9p2, | |
| VAn = 97,735 - 0,843 ґ 10-4p - 27,04 ґ 10-9p2. |
Данные уравнения справедливы для давления 2000 атм и выше. На основании этих результатов находим, что для реакции (9.62)
| DVреакции = -4,919 - 10,476 ґ 10-4p + 85,55 ґ 10-9p2 см3/молъ. | (9.63) |
Наряду с уравнением (9.57), уравнение (9.63) выражает скорость изменения свободной энергии реакции с изменением давления. Памятуя, что 1 cм3Чamм равно 0,02422 кал, разделим все численные величины в уравнении (9.63) на этот переводной коэффициент и получим
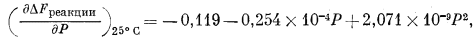 |
(9.64) |
где DFреакции дается в калориях, а Р - в атмосферах.
Из уравнения (9.64) видно, что даже при большом изменении давления величина DFреакции в нашем случае будет изменяться незначительно. Например, при 3000 атм
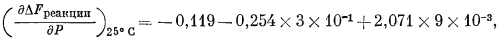 |
|
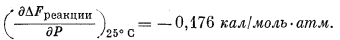 |
Таким образом, каждое изменение давления на 100 атм (в пределах до 3000 атм) будет вызывать изменение DFреакции всего лишь на -0,176 ґ 100 = -17,6 кал/моль.
Йодер и Уир приводят подобные уравнения и для следующих реакций:
| анальцим = жадеит + вода, анальцим + кварц = альбит + вода. |
Скорость изменения свободной энергии реакции с изменением давления при постоянной температуре определяется уравнением
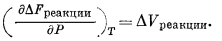 |
(9.57) |
Как правило, мольный объем каждого компонента,
участвующего в реакции, зависит от температуры и давления, а
следовательно, DVреакции тоже
будет зависеть от этих переменных. Для некоторых реакций DVреакции практически постоянно и
уравнение (9.57) можно решить посредством прямого интегрирования. В других
случаях величина DVреакции
выражается в виде серии многочленов, решаемых относительно давления для
каждой температуры; здесь уравнение (9.57) решается путем
последовательного частного интегрирования. Приведены примеры,
иллюстрирующие высказанные положения. Представлен расчет равновесного
давления для различных температур.
Если реакция между фазами постоянного состава протекает при меняющихся температуре и давлении, то суммарное изменение свободной энергии этой реакции будет определяться уравнением
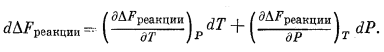 |
(9.65) |
Имея в виду уравнения (9.49) и (9.57), уравнение (9.65) можно переписать следующим образом:
| dDFреакции = -DSреакции dT + DVреакции dP. | (9.66) |
Если система равновесна, то dDFреакции = 0 и уравнение (9.66) принимает вид
| DVреакции dP - DSреакции dT = 0, | (9.67) |
откуда
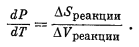 |
(9.68) |
Далее из уравнения (9.46)
| DFреакции = DHреакции - T DSреакции. |
Для равновесных условий DFреакции = 0, а
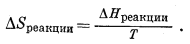 |
(9.69) |
Таким образом, уравнение (9.68) можно выразить иначе:
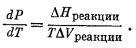 |
(9.70) |
Выражение (9.70) обычно называют уравнением
Клапейрона.
Использование приведенных выше уравнений, а также практическое применение некоторых термохимических соотношений, рассмотренных в предыдущих разделах, мы можем проиллюстрировать на примере системы гематит - гётит - вода, экспериментальное изучение которой выполнено Шмальцем [21]. Этот исследователь изучал реакцию
|
(9.71) |
при повышенных температурах и давлениях. Полученные им результаты сведены на фиг. 9.7.
Данная система представляет собой пример моновариантного равновесия, ибо она характеризуется всего лишь одной степенью свободы. Так, каждой данной температуре, например, соответствует одно определенное значение равновесного давления. Граница между находящимися в равновесии фазами определяется прямой линией с положительным наклоном, что вообще характерно для реакций с участием конденсированных фаз.
Наклон границы между фазами определен экспериментально: он составляет 22,3 бар/град, или в пределах экспериментальной ошибки 22,3 атм/град. (Переводной коэффициент из бар в атмосферы таков: 1 бар = 0,98692 атм.) Изменение объема при данной реакции (9.71) было рассчитано для 130° С и 1 атм. Предполагается, что величины теплового расширения двух участвующих в реакции твердых веществ в интервале от комнатной температуры до 130° С взаимно уравниваются, а на изменение объема воды при 130° С вводится соответствующая поправка. Отсюда DVреакции(130°C, 1 атм) = -6,8 см3. Теперь, зная DVреакции и отношение dP/dT, по уравнению (9.68) можно рассчитать и величину DSреакции:
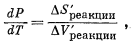 |
|
| DS'реакпии = -6,8 ґ 22,3 = -151,64 см3Чатм/градЧмоль, | |
| DS'реакпии = -151,64 ґ 0,02422 = -3,7 кал/градЧмоль. |
В этом выражении штрих у символа DSреакпии означает, что данная величина определена для частных условий 130° С и 1 атм и пересчитана на 1 моль гематита.
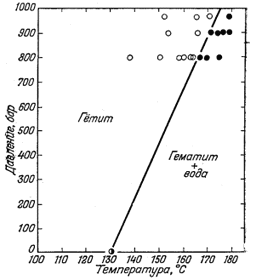 |
| Фиг. 9.7. Граница между фазами гётит -
гематит. Светлыми кружками показаны эксперименталь- |
При оценке термодинамических свойств гётита для стандартного состояния при 25° С Шмальц рассуждал следующим образом. Как мы указывали выше, с достаточной острожностью можно предположить, что DСP реакции (9.71) на температурном интервале от 25 до 130° С остается постоянной. Из уравнения (9.9) при Р = 1 и неизменной величине DCP мы имеем
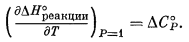 |
(9.72) |
Интегрирование уравнения (9.72) для DCP = const дает следующий результат:
| DH°реакпии T2 - DH°реакпии T1 = DC°P(T2 - T1). | (9.72a) |
Подставив в это уравнение равенство Т1DS°реакпии T1 = DH°реакпии T1, получим
| DH°реакпии T2 = T1DS°реакпии T1 + DC°P(T2 - T1). | (9.73) |
Теперь можно подставить конкретные значения Т2 = 298° К (25° С) и T1 = 403° К (130° С). Только что мы рассчитали величину DS°реакпии при T1 и нашли, что она равна -3,7 кал/град. Теплоемкость гематита и воды известна, а данные о теплоемкости гётита отсутствуют. В то же время известны значения теплоемкости для корунда Аl2О3 и диаспора АlOОН. Предположим, что
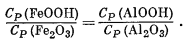 |
Исходя из подобного допущения, мы находим, что для гётита СP @ 18,7 кал/градЧмоль и, наконец, что DСP @ -5,6 кал/градЧмоль.
Подставим полученные результаты в уравнение (9.73) и найдем, что
| DH°реакпии 298 = (403)(-3,7) + (-5,6)(-105), | |
| DH°реакпии 25°C = -903 кал/моль. | (9.74) |
Согласно уравнению (9.48),
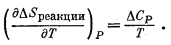 |
Для случая, когда Р = 1,
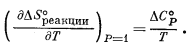 |
После интегрирования получаем
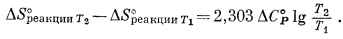 |
Для интересующих нас температур
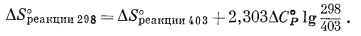 |
Отсюда
| DS°реакпии 298 = -3,7 + (2,303) (-5,6)(-0,1311), | |
| DS°реакпии 298 = -2,0 кал/градЧмоль. | (9.75) |
Из уравнения (9.1)
| DF°реакпии 298 = DH°реакпии 298 - 298DS°реакпии 298. |
Таким образом, для рассматриваемой нами реакции
| DF°реакпии 298 = -903 - (298)(-2,0) = -307 кал/моль. |
Так как свободные энергии образования гематита и воды известны, то свободную энергию образования гётита можно рассчитать по величине свободной энергии реакции; такой расчет несложен:
| DF°реакции = 2DF°обр FeOOH - DF°обр Fe2O3 - DF°обр H2Oжидк, | |
| - 0,307 = 2DF°обр FeOOH - (-177,1) - (-56,69), | |
| DF°обр FeOOH = -117,0 ккал/моль. |
Сходным образом,
| DH°реакции = 2DH°обр FeOOH - DH°обр Fe2O3 - DH°обр H2Oжидк | |
| -0,903 = 2DH°обр FeOOH - (-196,5) - (-63,32), | |
| DH°обр FeOOH = -130,4 ккал/моль. |
И наконец,
| DS°реакции = 2S°FeOOH - S°Fe2O3 - S°H2Oжидк, | |
| -2,0 = 2S°FeOOH - 21,5 - 16,72, S°FeOOH = 18,1 кал/градЧмоль. |
В связи с приближенностью
определения СP для FeOOH (возможная ошибка ±1
кал/мольЧград), а также
потому, что наклон границы между фазами не был установлен
экспериментально, Шмальц оценил ошибку определения DF°обр FeOOH и DH°обр FeOOH в 1
ккал/моль, а ошибку в определении S°FeOOH
в ± 0,5 кал/градЧмоль.
В только что рассмотренном случае равновесная линия Р - Т предоставляет собой прямую; ее наклон составляет
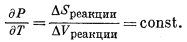 |
(9.76) |
|
1 (стр.282) См. работу Томпсона [22]. |
Постоянство отношения DSреакции/DVреакции при повышенных температурах и давлениях довольно точно сохраняется для реакций всех типов. При низких температурах для реакций между некоторыми твердыми веществами кривая Р - Т обнаруживает слабую вогнутость в сторону оси давлений. Для реакций, протекающих с образованием газа, кривая равновесия обычно характеризуется постепенным увеличением крутизны положительного наклона по мере того, как газ по своим свойствам приближается к жидкости. При повышенных температурах и давлениях значение dP/dT, как правило, положительно, хотя и имеются определенные исключения. Одним из таких исключений, например, является фазовый переход лед - жидкая вода.
При давлении 1 атм наклон линии равновесия может быть рассчитан по величинам DS°реакции и DV°реакции. Однако сам по себе этот расчет не покажет, постоянно ли отношение dP/dT. Положение линии равновесия на оси Т при Р = 1 атм в принципе можно вычислить по уравнению (9.1):
| 0 = DF°реакции = DH°реакции - TDS°реакции. |
Однако ошибки экспериментального определения величин
DH°реакции и DS°реакции обычно слишком велики,
чтобы можно было пользоваться подобного рода вычислениями. Томпсон [22]
показал, что для интересующих нас реакций ошибка определения температур
фазового перехода по уравнению (9.1) и по величинам DH°реакции, найденным путем измерения
теплоты растворения, имеет порядок ±400° С.
Основное соотношение, на которое опираются при графическом изображении свойств равновесных систем, выражается уравнением (1.11), а именно
| DF°реакции = - RT lnК. |
Поскольку сейчас наш интерес сосредоточен на вопросе о влиянии изменения температуры и давления на изменение свободной энергии реакции DFреакции, нам нужно вновь обратиться к уравнению (1.11) и некоторым другим следующим из него выражениям.
В качестве общего случая рассмотрим реакцию
| lА(аA) + mВ(аB) = nС(аC) + rD(аD), | (9.77) |
в которой можно видеть любые реагирующие компоненты и где величины активности aА, aB, aC и аD могут иметь самые различные значения. Общее давление может быть любым; сходным образом некоторые компоненты могут находиться под разным давлением или в случае газов обладать различными парциальными давлениями. Понятно, конечно, что активности продуктов реакции и реагентов должны быть измерены при одинаковой температуре.
Для удобства упростим используемые символы таким образом, чтобы FА = DFобр A и т. д., и напишем уравнение изменения свободной энергии реакции
| DFреакции = rFD + nFС - lFА - mFB, | (9.78) |
где FA обозначает мольную свободную энергию чистой фазы или парциальную мольную свободную энергию растворенного компонента.
Теперь рассмотрим ту же реакцию при условии, что каждый ее компонент взят в его стандартном состоянии, т. е. при активности, равной единице. Тогда мы будем иметь
| lА(aА = 1) + mВ(aB = 1) = nС(aC = 1) + rD(aD = 1). | (9.79) |
Изменение свободной энергии в таком случае составит
| DF°реакции = rF°D + nF°C - lF°A - mF°B. | (9.80) |
Величины F°A и т. д. соответствуют значениям свободной энергии компонентов в их стандартном состоянии. Стандартное состояние вещества определяется давлением 1 атм (или в случае реального газа фугитивностью, равной единице) при любой данной температуре. Следовательно, величины F°A, F°B, F°C и F°D ависят от температуры, таким образом DF°реакции зависит от температуры. Однако, согласно нашему определению стандартного состояния, величины F°A и т. д. не зависят от давления, т. е. DF°реакции тоже не зависит от давления.
Из уравнения (1.13) мы имеем
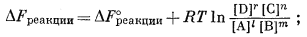 |
в этом выражении активности могут иметь любые значения. Поскольку DFреакции является функцией одновременно и температуры, и давления, а DF°реакции зависит только от температуры, то квотант активностей также будет зависеть и от температуры и от давления. В случае равновесия DFреакции = 0; вместе с тем в нашем распоряжении имеется уравнение (1.11), согласно которому
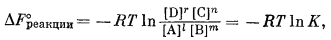 |
причем теперь все значения активности отвечают равновесному состоянию. Так как величина DF°реакции не зависит от давления, то и K не должен зависеть от давления. Однако если давление меняется, то и индивидуальные активности тоже могут изменяться, хотя величина К будет оставаться постоянной.
Для примера рассчитаем влияние повышения общего давления на реакцию
| 3Fекрист + 2O2 газ = Fe3O4 крист. | (9.81) |
Константа равновесия этой реакции определяется выражением
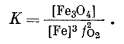 |
(9.82) |
Прологарифмируем его и получим
| lgК = lg[Fe3O4] - 3lg[Fe] - 2lgfO2. | (9.83) |
При 1 атм общего давления [Fе3О4] = [Fe] = 1, а поэтому уравнение (9.83) упрощается:
| lgK = -2 lgfO2. | (9.84) |
Величину lgK можно подсчитать по уравнению (1.11):
| DF°реакции = -RT lnK, |
но вначале надо найти DF°реакции по величинам DF°обр. Итак,
| DF°реакции = DF°Fe3O4 - 3DF°Fe - 2DF°O2. | |
| DF°реакции 25°C = -242,4 - 3(0) - 2(0) = -242,4 ккал/моль. При 25°С | |
| При 25°С | |
| DF°реакции = -1,364 lgK, |
а поэтому
| lgK = 177,7. | (9.85) |
Из уравнения (9.84) имеем
| -2lgfO2 = 177,7, | |
| fO2 = 10-88,9 аmм. |
При столь низком значении фугитивности кислород будет вести себя как идеальный газ, так что мы вправе заменить давление на фугитивность. Мы нашли, что для реакции (9.81) при 25° С и 1 атм общего давления равновесное парциальное давление кислорода составляет 10-88,9 аmм. К тому же результату мы пришли и в гл. 6.
Теперь проведем расчет равновесного парциального давления кислорода для той же реакции, но при 25° С и 1000 атм, общего давления. Вновь начнем с уравнения (9.83), хотя активности твердых веществ в таких условиях не будут равны единице. Характер изменения активности чистого вещества с изменением давления описывается уравнением (2.24)1 (стр.285), согласно которому
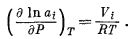 |
(9.86) |
После интегрирования и логарифмирования уравнение (9.86) приобретает следующий вид:
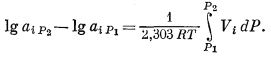 |
(9.87) |
По уравнению (9.87) можно вычислить активности Fe3O4 и Fе при 1000 атм (25° С). Поскольку при Р = 1 атм активности твердых веществ равны единице, то уравнение (9.87) для реакции (9.81) примет вид
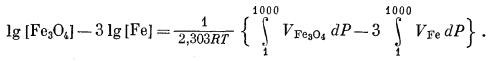 |
(9.88) |
Уравнение (9.88) можно упростить следующим образом:
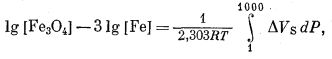 |
(9.89) |
где
| DVS = VFe3O4 - 3VFe. |
Достаточно правомерно предположить, что DVS постоянно. Сжимаемость Fe и Fе3O4 не только мала сама по себе, но и одинакова для этих двух веществ, объем которых с повышением давления уменьшается в одинаковой степени. Если DVS постоянно, то уравнение (9.89) можно проинтегрировать:
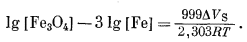 |
(9.90) |
При 25° С мольный объем VFe3O4 равен 44,52 см3, a VFe = 7,09 см3, следовательно, DVS = 23,25 см3. Подставим в уравнение (9.90) численные значения и получим
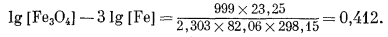 |
(9.91) |
|
1 (стр.285) В уравнении (2.24) объем обычно выражается в виде парциального мольного объема. Для чистых веществ его можно заменить мольным объемом. |
Теперь мы имеем все данные, необходимые для расчета fO2 при 1000 атм общего давления по уравнению (9.83), а именно
| lgК = lg[Fe3O4] - 3lg[Fе] - 2lgfO2. |
Подставим в него численные значения из уравнений (9.85) и (9.91)
| 177,7 = 0,41- 2lgfO2 | |
| 2lgfO2 = - 177,3, | |
| fO2 = 10-88,7 атм. |
Следовательно,
| РO2 = 10-88,7 атм |
(поскольку в таких условиях cO2 = 1).
Итак, при 1 атм общего давления и 25° С равновесное значение РO2 составляет 10-88,9 атм, а при общем давлении 1000 атм и той же температуре оно равно 10-88,7 атм, т. е. изменяется совсем незначительно.
На фиг. 9.3-9.5 вниманию
читателя предложено несколько диаграмм устойчивости минералов, в которых
координатами служат фугитивность одного из участвующих в реакции газов
(кислорода или серы) или соответствующая функция DF°реакции T и температура.
Все эти диаграммы построены для 1 атм общего давления. Если
проделать необходимые вычисления по тому методу, который был только что
изложен, то можно построить серию. подобных диаграмм устойчивости для
каждого интересующего нас давления. Однако мы только что показали, что
равновесные значения фугитивности с изменением давления почти не меняются.
А поэтому изобарические диаграммы устойчивости данного типа для повышенных
давлений не будут существенно отличаться от диаграммы, построенной для 1
атм. Этот вывод справедлив по меньшей мере в области умеренно
высоких давлений.
Задачи, касающиеся исследования равновесии между ионами в водных растворах при различных температурах и давлениях, решаются в общем теми же методами, какие были рассмотрены в предыдущем разделе в приложении к системе Fe - Fе3O4 - О2. Например, нам нужно рассчитать активность водородного иона в чистой воде при 35° С и 2000 атм. Для соответствующей реакции
| Н2Oжидк = Н+водн + ОН-водн |
константа равновесия К35° C будет равна
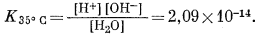 |
(9.92) |
Активность H2O и ОН- при 2000 атм можно рассчитать по уравнению (9.87). Для растворенных компонентов в этом уравнении мы используем величину -Vi, т. е. парциальный мольный объем этих компонентов. Подсчитанные таким образом значения активностей можно подставить в уравнение (9.92) и рассчитать тем самым величину аH+. Полученное значение и будет соответствовать равновесной активности водородного иона при 2000 атм и 35° С.
Итак, расчет равновесии для растворенных компонентов не отличается от подобного расчета для реакций иных типов, за тем лишь исключением, что требуется знание парциальных мольных объемов ионов. Эти термодинамические характеристики установлены для немногих ионов и вдобавок разбросаны в многочисленных работах. Данная проблема прекрасно освещена в работе Зена [24], кстати представляющей определенный интерес для геохимиков. Этот автор рассматривает различные способы определения парциальных мольных объемов солей по имеющимся экспериментальным данным и останавливается на вопросе о переходе от этих величин к парциальным мольным объемам ионов. В работе Зена имеется таблица подобных значений для ряда ионов и солей. Задача определения индивидуальных ионных объемов по объемам солей аналогична задаче определения коэффициентов активности индивидуальных ионов по среднесолевым коэффициентам активности: где-то в цепи рассуждений необходимо прибегнуть к допущению, выходящему за рамки термодинамики.
 |
 |
|
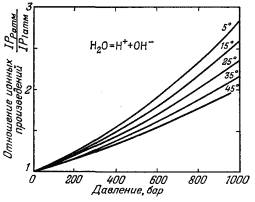
Фиг. 9.8. Ионное произведение воды [Н+] [ОН-] как функция давления при нескольких температурах. По данным Оуэна и Бринкли [13]. |
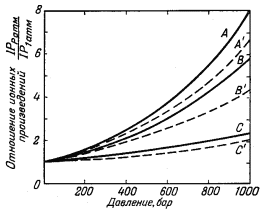
Фиг. 9.9. Влияние давления на ионные произведения
нескольких веществ, растворенных в воде (сплошные линии) и в
растворе 0,725 М NaCl (штриховые линии) при 25° С. |
Для соли, находящейся в равновесии с ее насыщенным раствором, уравнение равновесия можно написать в виде ионного произведения. Например, для реакции, определяющей равновесие кальцита
| CaCO3 крист = Са2+водн + СО2-3 водн, | (9.93) |
мы можем написать
| [Са2+][СO2-3] = [CaCO3] Kкальцит, | (9.94) |
а левую часть этого выражения [Са2+][СО2-3] - назвать ионным произведением. Это произведение часто называют произведением активности, а уравнение (9.94) обычно пишут без [CaCO3], очевидно подразумевая тем самым, что давление равно 1 атм.
Активность кальцита при повышенных давлениях можно вычислить с помощью уравнения (9.87), поскольку известна величина Vкальцит. Кроме того, известно значение Ккальцит, например при 25° С, а поэтому правая часть уравнения (9.94) рассчитывается для любого интересующего наc давления. Полученный результат соответствует величине ионного произведения для данного давления.
Оуэн и Бринкли [13]
вычислили ионные произведения для нескольких важных равновесных систем при
давлении до 1000 бар. Они исследовали равновесия в воде и в
растворе 0,725 М хлористого натрия. Часть полученных ими
результатов представлена на фиг. 9.8 и 9.9 в виде отношения ионного
произведения при некотором давлении Р атм к ионному произведению
при 1 атм.
Чрезвычайно важное соотношение определяется уравнением Вант-Гоффа: оно связывает константу равновесия с температурой. Продемонстрируем вывод этого уравнения.
На основании уравнений (9.49) и (9.46) мы имеем
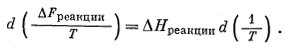 |
(9.95) |
Памятуя, что общее давление есть величина постоянная, перепишем уравнение (9.95) в следующем виде:
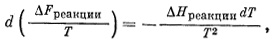 |
(9.96) |
Разделим обе части уравнения (9.96) на Т и несколько преобразуем его:
 |
(9.97) |
Левая часть уравнения (9.97) в точности соответствует d(DFреакции/T). Следовательно, уравнение (9.97) может быть преобразовано в уравнение
 |
(9.98) |
или в уравнение
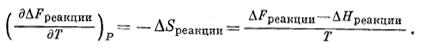 |
(9.99) |
Теперь зададимся стандартными условиями для термодинамических функций, входящих в уравнения (9.98) и (9.99); другими словами, вместо DFреакции подставим DF°реакции, а вместо DHреакции будем писать DH°реакции. Мы вправе сделать и еще одну подстановку, так как для равновесной системы
| DF°реакции = -RT lnK. |
Тогда из уравнения (9.98) мы имеем
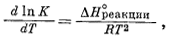 |
(9.100) |
a из уравнения (9.99)
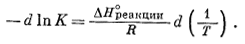 |
(9.101) |
Уравнение (9.100) и есть уравнение Вант-Гоффа; уравнение (9.101) представляет собой одну из его модификаций. Данные уравнения приложимы к системам, находящимся в равновесии; это обусловлено тем, что DF°реакции было заменено на -RT lnК. Уравнения (9.100) и (9.101) чрезвычайно полезны, поскольку для многих реакций величина DH°реакции постоянна на значительном температурном интервале, и, таким образом, эти уравнения легко интегрировать. Если DF°реакции постоянна, то уравнение (9.101) принимает следующий вид (после перевода натурального логарифма в десятичный):
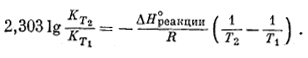 |
(9.102) |
При постоянной DH°реакции график значений lgК относительно 1/Т отвечает прямой линии с наклоном -DH°реакции/(2,303R). В качестве примера реакции, исследованной при повышенных температурах и давлениях, можно привести реакцию фазовых соотношений аннита КFе3АlSi3О10(ОН)2; реакция изучена Эйгстером и Уонзом [4]
|
(9.103) |
Эти исследователи пришли к выводу, что при всех рассмотренных давлениях константа равновесия реакции выражается уравнением
 |
Другими словами, зависимость lgK от 1/T выражается прямой линией с наклоном -9215 град. Отсюда
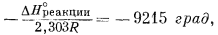 |
|
| DH°реакции = 2,303 ґ 9215 град ґ 1,987 кал/градЧмоль, | |
| DH°реакции = 42,2 ккал/моль. |
Если одновременно меняются и температура, и давление, то изменение свободной энергии реакции описывается уравнением
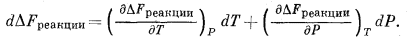 |
(9.65) |
При условии равновесия, когда dDFреакции = 0, уравнение (9.65) сокращается до хорошо известных выражений
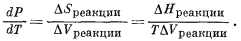 |
(9.68; 9.70) |
Используя уравнения (9.68) и (9.70) и зная мольные объемы и теплоемкости фаз, находящихся в равновесии, по экспериментальной Р - T-диаграмме можно вычислить различные термодинамические функции; это положение иллюстрируется примером. Рассмотрен характер изменения активности конденсированных фаз при повышении давления; на примере системы с участием кислорода и твердых веществ показано, каким образом меняется парциальное давление кислорода в зависимости от увеличения общего давления на эти твердые вещества. Влияние повышения давления на ионное равновесие рассмотрено на конкретном примере увеличения ионного произведения воды и ионного произведения растворенных солей, происходящего с ростом общего давления. Дан вывод уравнения Вант-Гоффа
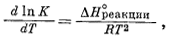 |
(9.100) |
и разобран пример, показывающий, как это уравнение можно
использовать.
9.1. Для реакции
Baкрист + Sромбич + 2O2 газ = BaSO4 крист
при 25° С рассчитайте, пользуясь таблицами приложения 2:
а) DH°реакции; б) DS°реакции; в) DF°реакции по уравнению (9.1).
Сопоставьте последний полученный вами результат с соответствующей
величиной в приложении 2.
9.2. Полагая,
что DC°P для реакции из
упражнения 9.1 с повышением температуры практически не меняется, вычислите
DF°реакции при 400° К,
пользуясь соотношением
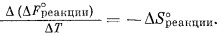
Ответ: DF°реакции = - 314,2
ккал/моль.
9.3. Подсчитайте
DH°реакции при 400° С для
реакции
H2 газ + 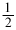 S2 газ =
H2Sгаз.
S2 газ =
H2Sгаз.
[См. уравнение
(9.14а).]
Ответ: DH°реакции = -20,5
ккал/моль.
9.4. По данным,
имеющимся в табл. 9.1 и 9.3, рассчитайте DH°обр и S° для силлиманита
при 1500° К.
Ответ: DH°обр = -597,3
ккал/моль; S° = 89,14 кал/градЧмоль. Какие дополнительные данные требуются для
вычисления DF°обр силлиманита
при 1500°К?
9.5. Рассчитайте наклон
графика значений DF°реакции
относительно температуры и предельное значение DF°реакции для реакции
3Feкрист + 2O2 газ = Fе3O4 крист,
считая уравнение (9.51)
справедливым.
Ответ: наклон = 0,0825
ккал/град; точка пересечения = -267,0
ккал.
9.6. Как было вычислено в
гл. 9, для реакции из упражнения 9.5 равновесное значение
РO2 при 25° С и 1000 атм общего
давления равно 10-88,7 атм. При этом мы пренебрегли
величинами сжимаемости, которые на 1 бар при 25° С составляют bFe3O4 = 5,5 ґ 10-7 бар-1 и bFе = 5,94 ґ
10-7 бар-1. Насколько оправдано такое
упрощение?
9.7. Плотность алмаза
составляет 3,51 г/см3, а графита 2,55
г/см3. Вычислите приближенно давление, при
котором эти две формы углерода будут равновесны при комнатной
температуре.
Ответ: Р @ 22 ґ 103
атм.
9.8. Определите константу
равновесия при 25° С для реакции
SrCO3 крист = Sr2+водн + СО2-3 водн.
Какова величина ионного произведения
[Sr2+][СО2-3] при 5000 атм, если
VSrCO3 = 38,9
см3?
Ответ: К =
10-9,16; ионное произведение =
10-5,7.
9.9. Для реакции
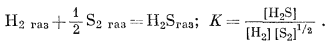
При наличии равновесия экспериментальным путем получены следующие данные:
| T°, K | lgK | T°, K | lgK |
| 1023 | 2,025 | 1362 | 0,902 |
| 1103 | 1,710 | 1405 | 0,793 |
| 1218 | 1,305 | 1473 | 0,643 |
| 1338 | 0,964 | 1537 | 0,490 |
Постройте по ним прямолинейный график; пользуясь
уравнением Вант-Гоффа, определите величину DH°реакции.
Ответ:
DH°реакции @ - 21
ккал.
9.10. Вычислите DF°реакции для каждой из температур,
перечисленных в упражнении 9.9, пользуясь соответствующими значениями
lgК. Постройте график значений DF°реакции относительно температуры и
определите наклон получившейся прямой. Сравните полученный наклон с
величиной DS°реакции
рассчитанной по DF°реакции 1023
и DH°реакции.
Ответ:
Наклон @ 0,0115 ккал/град; - DS°реакции = 0,0112
ккал/град.
1. В i r с h P., S c h a i r e r J. P., S p i с е r H. С.
Handbook of physical constants, Geol. Soc. Am., Spec. Paper 36,
1942.
2. C o b b l e J.W.A method for predicting thermodynamic
properties of electrolytes up to 350°C; Symposium on High Temperature
Solution Chemistry, 141 Meeting, Am; Chem. Soc., Wash., D. C., 1962.
3.
С r i s s C. M. Thermodynamic properties og high-temperature aqueous
solutions; Ph. D. dissertation, Purdue Univ., 1961.
4. E u g s t e r H.
P., W o n e s D. R. Stability relations of the ferruginous biotite,
annite, Journ. Petrology, 3, 82, 1962.
5. H o l l a n d H. D. Some
applications of thermochemical data to problems of ore deposits, I,
Stability relations among the oxides, sulfides, sulfates, and carbonates
of ore and gangue metals, Econ. Geol., 54, 184, 1959.
6. К е 1 1 е у К.
К. High-temperature heat-content, heat-capacity, and entropy data for -the
elements and inorganic compounds, U.S. Bureau of Mines Bulletin 584,
1960.
7. К е 1 1 е у К. К., K i n g E.G. Entropies of the elements and
inorganic compounds, U.S. Bureau of Mines Bulletin 592, 1961.
8. K e n
n e d y G. C. Pressure-volume-temperature relations in water at elevated
temperatures and pressures, Am. Journ. Sci., 248, 540, 1950.
9. К 1 о t
z I. Chemical Thermodynamics, Englewood Cliffs, N. J., Prentice-Hall,
1950.
10. L e w i s G. N., R a n d al l M. Thermodynamics, New York,
McGraw-Hill, 1923.
11. L e w i s G. N., R a n d a l l M.
Thermodynamics, 2nd ed., revised by Pitzer K. S., Brewer L., New York,
McGraw-Hill., Appendix 7, 669-686, 1961.
12. M a i e г С. G., К е 1 1 е
у К. К. Journ. Am. Chem. Soc., 54, 3243, 1932.
13. Owen В. В., Brinkley
S. R., J г. Calculation of the effect of pressure upon ionic equilibria in
pure water and in salt solutions, Chem. Revs., 29, 461, 1941.
14. R i с
h a r d s о n F. D., J e f f e s J. H. E. The thermodynamics of substances
of interest in iron and steel making from 0°C to 2400°C, I, Oxides, Joum.
Iron Steel Institute, 160, 241, 1948.
15. R i c h a r d s o n F. D., J
e f f e s J. H. E.. W i t h e r s G. The thermodynamics of substances of
interest in iron and steel making from 0°C to 2400"C, II, Compounds
between oxides, Journ. Iron Steel Institute, 166, 213, 1950.
16. R i c
h a r d s o n F. D., J e f f e s H. E. The thermodynamics of substances of
interest in iron and steel making from 0°C to 2400°C, III, Sulphides,
Journ. Iron Steel Institute, 171, 165, 1952.
17. R о b i e R. A.
Thermodynamic properties of selected minerals and oxides at high
temperatures, Trace Elements Investigations Report 609, U.S. Geol. Surv.,
September, 1959.
18. R o b i e R.A., B e t h k e P.M. Molar volumes and
densities of minerals. Trace Elements Report of Investigation 822, U.S.
Geol. Surv., 1962.
19. R o s s i n i F. D. et al. National Bureau of
Standards Circular 500, U.S. Dept. of Commerce, 1952.
20. S k i n n e r
B.J., C l a r k S. P., Apploman D. E. Am. Journ. Sci., 259, 651,
1961.
21. S c h m a l z R. F. Journ. Geoph. Res., 64, 575, 1959.
22.
T h o m p s o n J. В., Jr. The thermodynamic basis for the mineral facies
concept, Am. Journ. Sci., 253, 65, 1955. (Есть русский перевод: Т о м п с
о н Дж.Б. Термодинамические основы теории минеральных фаций. В кн.
"Вопросы теоретической и экспериментальной петрологии"., M., ИЛ,
1963.)
23. Y о d e r H..S., J г., W e i r С. E. Am. Journ. Sci., 258A,
420, 1960; 249, 683, 1951. (Есть русский перевод: И о д е p X. С., В а и р
К. Е. Теория анальпима, существующая при высоком давлении, и изменение
свободной энергии реакции с анальцимом при увеличении давления. В кн.
"Вопросы теоретической и экспериментальной петрологии", М., ИЛ,
1963.)
24. Z e n E' a n. Partial molar volumes of some salts in aqueous
solutions, Geochim. et Cosmochim. Acta, 12, 103, 1957.
F y f e W.S., T u r n e r F.J., V e r h o o g e n J.
Metamorphic Reactions and Metamorphic Facies, Gcol. Soc. Am. Memoir 73,
1958. (Есть русский перевод: Ф а и ф У., Т е р н е р Ф., Ф е р х у г е н Д
ж. Метаморфические реакции и метаморфические фации, М., ИЛ, 1962).
K l
o t z I. Chemical Thermodynamics, Englewood Cliffs, N. J., Prentice-Hall,
1950.
L e w i s G. N., R a n d a 1 1 М. Thermodynamics, 2nd ed.,
revised by Pitzer K. S., Brewer L., New York, McGraw-Hill, 1961.
T h o
m p s o n J.B., Jr. The thermodynamic basis for the mineral facios
concept. Am. Journ. Sci., 253, 65, 1955. (Есть русский перевод: Т о м п с
о н Дж.Б. Термодинамические основы теории минеральных фаций. В кн.
"Вопросы теоретической и экспериментальной петрологии", М., ИЛ, 1963.)
|
|
|
|
[Содержание] [Глава 8] [Глава 10] |