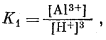
| Р.М. Гаррелс, Ч.Л. Крайст | Растворы, минералы, равновесия |
|
|
|
|
[Содержание] [Глава 9] [Глава 11] |
|
|
|
|
В предыдущих главах, в
которых основное внимание обращалось на зависимость соотношений
устойчивости минералов от парциального давления газов или Eh и рН, была
показана возможность использования диаграмм только двух типов. Однако
равновесные соотношения между минералами можно представить в виде функции
любых переменных, отражающих взаимосвязи между минералами в равновесной
химической реакции, К подобного рода переменным относится активность
растворенных молекулярных или ионных частиц в водном растворе. Ниже на
примере силикатов и карбонатов будет продемонстрировано, каким образом
можно изучать равновесие между минералами, используя для этой цели
переменные, наиболее удобные для исследователя.
Если допустить, что силикатные минералы находятся в равновесии с омывающими их перовыми водами, то соотношения между этими минералами можно выразить в виде функций активности ионов в поровом растворе. Мы располагаем далеко не полными термохимическими данными по силикатам, а те, что имеются, характеризуются различной степенью точности, Поэтому целесообразно составлять качественные диаграммы, выражая последовательность отложения минералов, которую следует ожидать при достижении равновесия, лишь графически.
Рассматриваемые ниже
диаграммы были построены при исследовании соотношений между силикатными
минералами в зоне выветривания, на небольшой глубине, куда проникают
грунтовые воды, и в осадочных образованиях, претерпевших слабое
диагенетическое изменение. Для подобных условий вполне пригодны диаграммы,
рассчитанные для 25° С и 1 атм общего давления.
Суть проблемы происхождения бокситов заключается в выяснении соотношений между каолинитом (H4Al2Si2O9) и гиббситом (Al2O3Ч3H2O). Во многих районах каолинит, безусловно, представляет собой последний минерал, который образуется перед окончательным растворением твердых компонентов породы под воздействием агентов выветривания. Однако в ряде мест таким устойчивым минералом оказывается гиббсит. Если допустить наличие равновесия между каолинитом, гиббситом, растворенным кремнеземом и водой, то можно написать следующее уравнение:
|
(10.1) |
sВ условиях глубокого выщелачивания, которые характерны для образования гиббсита, поровые воды бывают практически чистыми, что позволяет считать их активность постоянной и равной единице. Тогда константа равновесия для уравнения (10.1) будет равна
| [H4SiO4]2 = К. | (10.2) |
Подставив в уравнение (10.1) значения свободной энергии, получим
| DF°реакции = DF°обр гиббсита + 2DF°обр H2SiO4 - DF°обр каолинита - 5DF°обр H2O, | |
| DF°реакции = - 554,6 + 2(- 300,3) - (-884,5) - 5(- 56,69), | |
| DF°реакции = 12,7 ккал = -1,364 lg[H4SiO4]2, | (10.3) |
| K1/2 = [H4SiO4] = 10-4,7. | (10.4) |
Следовательно, равновесие между гиббситом и каолинитом достигается при определенной величине активности (= концентрации) растворенного кремнезема, составляющей примерно 2 ч. на млн. (в виде 1148104) или 1 ч. на млн. (в виде SiO2). При любой активности растворенного кремнезема ниже этого значения каолинит будет инконгруентно растворяться из-за недостатка кремнезема в растворе, а гиббсит накапливаться. Но чем же контролируется содержание кремнезема в почвенном растворе?
Дополнительные сведения в этом отношении может дать такое рассуждение: раз гиббсит находится в равновесии с поровой водой, то он будет равновесен и с различными продуктами своей диссоциации. Другими словами,
| Аl2O3ЧН2Oкрист + 6Н+водн = 2Аl3+водн + 6Н2Ожидк, | (10.5) |
| Аl2O3Ч3Н2Oкрист = 2Н+водн + 2АlO-2 водн + 2Н2Oжидк. | (10.6) |
Для этих реакций константы равновесия можно получить обычным путем, пользуясь величинами DF°обр. Для реакции (10.5)
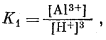 |
(10.7a)1 (стр.294) |
| lgK1 = 5,7 = lg[Al3+] + 3pH. | (10.7б) |
Для уравнения (10.6)
| K = [Н+][AlO-2], | |
| lgK2 = -14,6 = lg[AlO-2] - pH. |
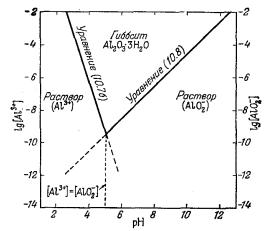
На фиг. 10.1 приведен
график, построенный по уравнениям (10.76) и (10.8). Он показывает, что
поле устойчивости гиббсита можно ограничить линиями [А13+] и
[АlO-2]. Соотношения, отраженные на фиг. 10.1, в
общем показывают, каким должно быть поведение гиббсита. Он будет
растворяться с образованием иона алюминия в кислой среде и с образованием
алюминат-инона в щелочной. Активность этих ионов уравнивается при рН =
5,1. Однако приведенный график нельзя принимать за точную диаграмму
растворимости, поскольку в водном растворе алюминий образует и многие
другие ионы,- особенно, в области кислых растворов, где небольшой (по
размеру) ион Al3+ по-видимому, связывается в комплексы со
многими анионами. Однако мы исходим из того, что в разбавленных растворах
содержание алюминия должно быть очень низким и недостаточно для осаждения
алюминия при большинстве значений рН.
|
1 (стр.294) Величина K1, приводимая для уравнения (10.7а), фактически является квадратным корнем из константы равновесия данной реакции в том виде, как составлено ее уравнение. Подобное упрощение делается не только в этом, но и в других сходных случаях. |
Гиббсит почти постоянно сопровождается одной или двумя формами гидроокиси алюминия (Аl2О3ЧН2О) - бёмитом и диаспором. Соотношения этих минералов между собой и с гиббситом определяются условиями выветривания, несмотря на то что все они в чистой воде метастабильны. Ниже приведено уравнение соответствующей реакции при стандартных условиях:
|
Такое изменение свободной энергии очень мало, но все же оно благоприятствует образованию диаспора. Этот вывод соответствует (наблюдаемым) условиям образования и относительной устойчивости бёмита и диаспора в процессах выветривания.
 |
 |
|
Фиг. 10.1. Устойчивость гиббсита, выраженная через рН и активность ионов двух- и трехвалентного алюминия, при 25° С и 1 атм. Номера уравнений соответствуют номерам в тексте. |
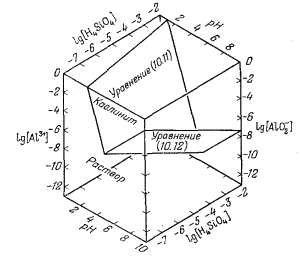
Фиг. 10.2. Поле устойчивости каолинита, определяемое процессами диссоциации этого минерала на А13+, АlO-2, Н+ и H4SiO4, при 25° С. |
Гиббсит связан с диаспором следующим уравнением реакции:
| Аl203 Ч Н2Окрист = Аl2О3 Ч 3Н2Окрист + 2Н2Ожидк. |
В присутствии чистой воды реакция смещается влево, причем происходит выделение нескольких килокалорий тепла. Это свидетельствует о том, что диаспор должен гидратировать до гиббсита. При комнатной температуре реакция протекает чрезвычайно медленно, однако мы вправе предположить, что (совместное) присутствие гиббсита и диаспора может контролироваться двумя факторами: во-первых, метастабильностью образования и существования диаспора и, во-вторых, тем, что диаспор образуется в периоды обезвоживания, когда активность воды много ниже активности чистой воды. При последующем повышении влажности диаспор существует только метастабильно.
Устойчивость каолинита можно описать так же, как это мы сделали для гиббсита. Ниже приведены реакции диссоциации этого минерала:
| H4Al2Si2O9 + 6Н+водн = 2Аl3+водн + 2H4SiO4 водн + Н2Ожидк, | (10.9) |
| Н4Аl2Si2O9 + 3Н2Oжидк = 2Н+водн + 2АlO-2 + 2Н4SiO4 водн. | (10.10) |
Константа равновесия для реакции (10.9)
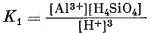 |
|
| lgK1 = 1,0 = lg[Al3+] + lg[H4SiO4] + 3pH. | (10.11) |
Константа равновесия для реакции (10.10)
| K2 = [H+][AlO-2][H4SiO4], | |
| lgK2 = -19,3 = lg[AlO-2] + lg[H4SiO4] - pH. | (10.12) |
Уравнения (10.11) и (10.12), описывающие диссоциацию каолинита, аналогичны уравнениям диссоциации гиббсита (10.76) и (10.8), за тем лишь исключением, что в уравнениях (10.11) и (10.12) содержится дополнительный символ растворенного кремнезема. В связи с появлением этой новой переменной соотношения устойчивости каолинита должны изображаться на объемной диаграмме, а не на плоской. Такое построение приведено на фиг. 10.2; область каолинита здесь ограничена двумя пересекающимися плоскостями, соответствующими уравнениям (10.11) и (10.12). На фиг. 10.2 эти плоскости обозначены номерами уравнений. При таком построении на передней плоскости диаграммы активность кремнезема равна 10-8, а на задней 10-2,0. В остальном чертеж пояснений не требует.
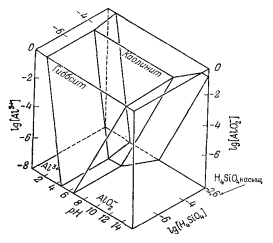 |
| Фиг. 10.3. Поля устойчивости гиббсита и каолинита, выраженные через рН и активность продуктов диссоциации Al3+, АlO-2 и H4SiO4, при 25° С и 1 атм. |
Геометрический рисунок на передней плоскости диаграммы (при постоянной [H4SiO4]) подобен графику (фиг. 10.1), отражающему устойчивость гиббсита. С увеличением [H4SiO4] устойчивость каолинита возрастает и становится максимальной в растворах, насыщенных по отношению к аморфному кремнезему. Концентрация насыщения установлена по данным экспериментального определения растворимости H4SiO4; она составляет 10-2,6 и ее можно численно приравнять к активности кремнезема в разбавленных растворах.
Итак, мы рассмотрели гиббсит и каолинит отдельно один от другого. Учитывая, однако, что поле устойчивости гиббсита может быть показано в пределах объемной диаграммы с использованием в качестве переменных рН, Аl3+, АlO-2 и H4SiO4, даже несмотря на то, что устойчивость гиббсита как такового не зависит от [H4SiO4], представляется возможным объединить фиг. 10.1 и 10.2 в одну (фиг. 10.3). В соответствии с уравнениями (10.1) и (10.2) границей между гиббситом и каолинитом будет служить плоскость, характеризующая определенную активность H4SiO4. По-видимому, при активности H4SiO4, превышающей эту величину, каолинит будет конгруентно растворяться без образования гиббситового остатка. Преобладание каолинита в горизонте А большинства почв, формирующихся в условиях глубокого выщелачивания, заставляет предполагать, что состав большей части почвенных растворов сдвинут в сторону задней плоскости диаграммы (фиг. 10.3).
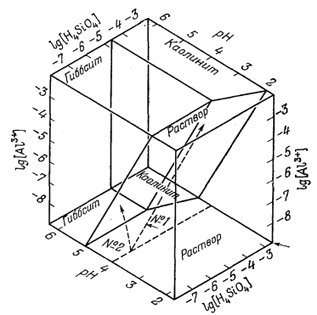
На фиг. 10.4 приведена более крупномасштабная диаграмма, показывающая соотношения гиббсита и каолинита в виде функции [Al3+], а не в виде функции [Аl3+] и [АlO-2] одновременно, как на фиг. 10.3. Ось рН на фиг. 10.4 направлена в другую сторону, чтобы яснее показать соотношения между раствором и твердыми веществами в области кислых растворов. Штриховые линии со стрелками показывают направления изменения состава раствора, происходящего в случае растворения каолинита при некотором значении рН. В таких условиях отношение H4SiO4 к Al3+ в растворе остается равным единице [см. уравнение (10.9)]. Если каолинит в почве подвергается выщелачиванию дождевыми водами при рН 4, а под влиянием растительности или разлагающегося органического вещества в почвенную воду выделяется CO2, состав раствора будет изменяться по линии, обозначенной стрелкой № 1; эта линия пересечет область устойчивости каолинита. Другими словами, в данном случае каолинит растворяется конгруентно с сохранением каолинитового остатка. С другой стороны, если величина рН не буферируется (не поддерживается постоянной), ионы Н+ будут расходоваться на растворение каолинита, а состав раствора будет
 |
|
Фиг. 10.4. Соотношения между гиббситом, каолинитом
и раствором при 25° С и 1 атм. |
изменяться примерно по линии, отмеченной стрелкой № 2; эта линия показывает инконгруентное растворение каолинита, приводящее к образованию гиббситового остатка.
Итак, анализ рассмотренных
выше диаграмм привел нас к предположению о существовании некоторых важных
факторов контроля образования бокситов. Это еще раз подчеркивает ценность
предлагаемых методов графического анализа и стимулирует сбор данных по
таким соотношениям, которые иным способом вывести невозможно. Большая
часть почв в районах с сильными ливневыми дождями и, соответственно, с
высокими скоростями выщелачивания является каолинитовой; для этих почв
характерно и низкое значение рН. По-видимому, снижение рН отчасти
обусловлено высоким содержанием СО2 в почвенном воздухе этих
районов (что вызвано разложением органических веществ в почве), а отчасти
связано с понижением рН на поверхности корней. Возможно, в условиях
чрезвычайно обильных осадков и жаркого климата бактериальное разложение
происходит настолько быстро, что углекислота, освобождающаяся при
разложении органического вещества, непосредственно поступает
в атмосферу, а почвы выщелачиваются так глубоко, что растительный слой
оказывается сравнительно слабо выраженным. При таких условиях в дождевых
водах, просачивающихся через почву, величина рН не будет поддерживаться
постоянной, в результате чего сможет создаваться гиббситовый остаток.
Какими бы ни были детали этого процесса, образование бокситов требует
обильных почвенных вод с небуферируемым рН, а также наличия
низкокремнеземистых и высокоглиноземистых остаточных почв. Этот вывод
подкрепляется анализами грунтовых вод Ямайки, дренирующих породы,
сложенные смесью каолинита и боксита [3]. Содержание кремнезема в этих
водах составляет 3-6 ч. на млн. Оно близко к значению 1 ч. на млн. (в виде
SiO2), т. е. той концентрации, которая, согласно нашим
предположениям, соответствует равновесию между гиббситом и каолинитом.
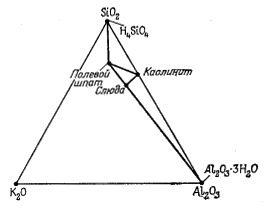 |
|
Фиг. 10.5. Теоретические ассоциации в системе, содержащей полевой шпат, oслюду, каолинит, гиббсит и аморфный кремнезем, при 25° С и 1 атм. В устойчивой системе, где вместо H4SiO4 присутствует кварц, ассоциация полевой шпат - каолинит, по-видимому, должна замещаться ассоциацией слюда - кварц. |
Фиг. 10.2 и 10.3 могут служить хорошей иллюстрацией того, как с увеличением числа фаз в системе при постоянном количестве компонентов поле устойчивого существования определенной фазы сужается. Отсюда следует, что значение такой фазы, как индикатора среды, возрастает. На фиг. 10.2 анализировалось поведение одного каолинита; фиг. 10.3 показывает, что введение в систему гиббситовой фазы сужает поле существования каолинита. Из фиг. 10.3 следует, что каолинит может устойчиво существовать только с таким раствором, в котором содержание Н4SiO4 колеблется от достаточного для силификации гиббсита до насыщенного в отношении аморфного кремнезема. Чем меньше поле устойчивого существования минерала, тем больший интерес он представляет для геохимиков: нужно лишь, чтобы его поле ограничивалось условиями, часто встречающимися в природе. Добавление в нашу систему Al2O3 - SiO2 - H2O еще одного компонента, а именно K2O, при низких температурах и давлениях позволяет исследовать поведение двух новых очень интересных фаз - калиевого полевого шпата и калиевой слюды. Прежде чем перейти к выбору растворенных форм, позволяющих наилучшим образом описать равновесные соотношения в такой системе, следует рассмотреть диаграмму состав - парагенезис, которая поможет нам составить уравнения реакций. На фиг. 10.5 представлена треугольная диаграмма состава для системы K2O - Al2O3 - SiO2 - H2O. Поскольку допускается, что со всеми минералами данной системы ассоциирует почти чистая вода, достаточно ограничиться лишь треугольником К2O - Al2O3 - SiO2, а состав гидратированных фаз проектировать из их точек в полной диаграмме-тетраэдре. Для высоких температур установлены следующие равновесные фазовые ассоциации: калиевый полевой шпат - калиевая слюда, калиевый полевой шпат - каолинит, калиевая слюда - каолинит, калиевая слюда - гиббсит, каолинит - гиббсит, калиевый полевой шпат - H4SiO4, каолинит - Н4SiO4. Для высокотемпературных условий вместо Н4SiO4 (аморфного кремнезема) в последних двух парагенезисах обычно рассматривают кварц. Однако, как показал Сивер [б], максимальная растворимость кремнезема при низкой температуре контролируется именно аморфным кремнеземом, а не кварцем. Скорость кристаллизации кварца оказывается столь низкой, что для большинства низкотемпературных процессов за верхний предел содержания растворенного кремнезема в природных водах следовало бы принять метастабильную фазу аморфного кремнезема.
Если написать уравнения реакций, соответствующие перечисленным выше парагенезисам, обнаружится, что в этих реакциях участвуют только три переменные: [К+], [Н+] и [H4SiO4]. Вместе с тем отношение [К+] к [H+] в различных константах равновесия почти всегда равно единице. Следовательно, все соотношения между минералами можно представить на двумерной диаграмме с отношением [К+]/[H+] по одной оси и активностью Н4SiO4 по другой. Напишем все уравнения реакций и их константы равновесия:
|
(10.13) | ||||||||||||||||||||||
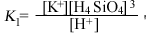 |
|||||||||||||||||||||||
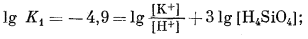 |
(10.14) | ||||||||||||||||||||||
|
(10.15) | ||||||||||||||||||||||
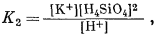 |
|||||||||||||||||||||||
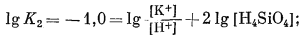 |
(10.16) | ||||||||||||||||||||||
|
(10.17) | ||||||||||||||||||||||
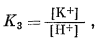 |
|||||||||||||||||||||||
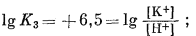 |
(10.18) | ||||||||||||||||||||||
|
(10.19) | ||||||||||||||||||||||
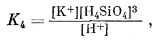 |
|||||||||||||||||||||||
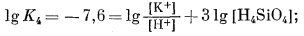 |
(10.20) | ||||||||||||||||||||||
|
(10.21) | ||||||||||||||||||||||
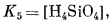 |
|||||||||||||||||||||||
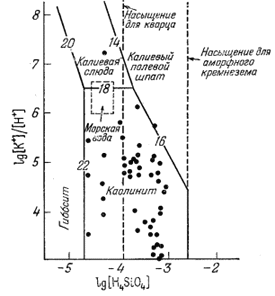
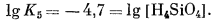 |
(10.22) | ||||||||||||||||||||||
 |
|
Фиг. 10.6. Устойчивые соотношения некоторых фаз в
системе К2О - Al2O3 -
SiO2 - Н2О при 25° С и 1 атм,
выраженные в виде функции [К+]/[H+] и
[H4SiO4]. |
Перечисленные соотношения
графически изображены на диаграмме фиг. 10.6, осями координат которой
служат [K+]/[H+] и lg[H4SiO4]
Среди многих интересных закономерностей, которые обнаруживаются при
анализе этой диаграммы, отметим следующие. Состав значительной части
подземных и речных вод попадает в поле устойчивости каолинита. Содержание
кремнезема в этих водах, как правило, не выходит за пределы концентраций,
характеризующих растворимость кварца и аморфного кремнезема (жирные
точки). Слюда и каолинит представляются промежуточными фазами в процессе
бокситизации калиевого полевого шпата. Ассоциация каолинита с калиевым
полевым шпатом, столь часто устанавливаемая при исследовании продуктов
выветривания, метастабильна и возникает только вследствие низкой скорости
кристаллизации кварца при пониженных температурах. Положение основной
массы точек, отвечающих результатам анализа природных вод, находится в
соответствии с "агрессивностью" большинства речных и подземных вод,
вызывающих каолинитизацию породообразующих минералов. При очень медленном
просачивании "чистой" дождевой воды (H2O в равновесии с
давлением СО2, равным 10-3,5 атм) через
аркозовый песчаник, состоящий из одного калиевого полевого шпата, состав
воды будет меняться от состава почти чистой Н2О до состава,
отвечающего границе между гиббситом и каолинитом. При этом он пройдет
через тройную точку гиббсит - каолинит - слюда и дойдет до точки каолинит
- слюда - полевой шпат. Было бы интересно получить серию анализов
подземных вод из слюдяных аркозов в зависимости от длины пути
просачивания. Результаты подобных анализов дали бы необходимую информацию
об относительных скоростях установления равновесия воды с полевым шпатом и
слюдой. Содержание кремнезема в большей части природных вод превышает
значение, которое можно было бы предсказать, исходя из реакций с калиевой
слюдой и калиевым полевым шпатом; очевидно, оно повышается за счет других
минералов, которые приходят к равновесию быстрее, чем калиевый полевой
шпат.
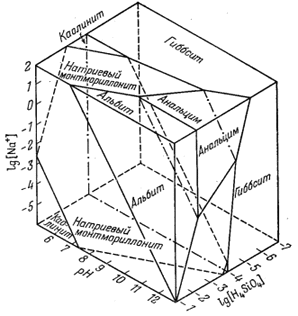
Соотношения, только что выведенные для системы К2О - Аl2O3 - SiO2 - Н2О, сразу же вызывают у исследователя вопрос о фазовых соотношениях в аналогичной системе Na2O - Аl2O2 - SiO2 - H2O. На фиг. 10.7 приведена диаграмма, построенная после составления уравнений реакций, подобных уравнениям между фазами в системе с K2O. Однако для альбита и анальцима мы не располагаем удовлетворительными данными о величине
 |
|
Фиг. 10.7. Устойчивые соотношения некоторых фаз в
системе Na2O - Al2O3 -
SiO2 - Н2О при 25° С и 1 атм,
выраженные в виде функции [Na+], pH и
[H4SiO4]. |
свободной энергии. Поэтому при общей правильности
геометрических соотношений, выведенных на основании констант равновесия,
численные значения переменных по осям координат диаграммы являются сугубо
приближенными. Эта диаграмма получена нами от Кэрта Линна (личное
сообщение, 1959), который экстраполировал соотношения, выведенные
экспериментально для высоких температур и давлений, до условий комнатной
температуры. Пришлось воспользоваться трехмерной диаграммой, так как в
константах равновесия натриевого монтмориллонита отношение
[Na+]/[H+] не равно единице. Граница анальцим -
альбит помещена за пределом насыщения раствора
H4SiO4, поскольку в осадочных породах анальцим
обычно встречается вместе с халцедоном, что заставляет предполагать тесную
ассоциацию анальцима с аморфным кремнеземом. Вместе с тем присутствие
аутигенного альбита указывает на то, что реакция анальцим + аморфный
кремнезем = альбит + вода, относящаяся к категории "либо идущих, либо
неидущих"1 (стр.301), при комнатной
температуре, вероятно, идет влево, а при несколько повышенной температуре
- вправо. Во всяком случае, при комнатной температуре анальцим возникает
при высоком отношении [Na+]/[H+], т. е. из щелочных
натриевых вод.
Для систем, содержащих MgO,
как и для систем с участием Na2O, мы не располагаем
необходимыми данными по свободным энергиям. Однако, как и в предыдущем
случае, имеется возможность дать качественное выражение устойчивости
минералов как функции активностей ионов в водной среде. Приближенный
расчет устойчивых соотношений при комнатной температуре в системе с
участием чистого магнезиального хлорита, флогопита, каолинита, калиевой
слюды и калиевого полевого шпата проделан Линном (личное сообщение, 1959).
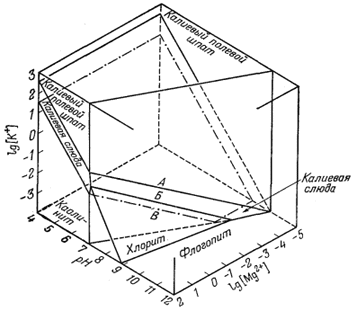
Результаты, полученные Линном, представлены на фиг. 10.8. Цифрам на осях
координат доверять не следует, но общая конфигурация диаграммы сопоставима
с результатами, полученными экспериментальным путем при высокой
температуре (Хемли, личное сообщение, 1960). Вероятно, самая интересная
особенность этой диаграммы определяется
|
1 (стр.301) 1 См. примечание на стр. 20.- Прим. ред. |
соотношениями устойчивости, четко видимыми на передней стенке: все минералы - хлорит, флогопит, каолинит, калиевый полевой шпат и мусковит - устойчивы в относительно узком интервале значений [К+] и рН при данной величине [Mg2+]. По-видимому, описываемый случай отвечает соотношениям между этими минералами и морской водой, в которой обломочные минералы могут существовать в течение длительного промежутка времени, испытывая очень слабое изменение.
Морская вода в некотором смысле может рассматриваться как раствор, который пытается "приспособиться" ко всем вносимым в него минералам. Хотя это не столь очевидно, состав морской воды очень слабо отличается
 |
|
Фиг. 10.8. Предварительная диаграмма, показывающая
вероятные устойчивые соотношения в части системы K2O -
MgO - FeO - Al2O3 - SiO2 -
H2O при 25° С и 1 атм. |
от равновесного по отношению к огромному числу фаз, а из-за низкого химического потенциала скорость изменения нестабильных компонентов раствора также будет исчезающе мала.
Помимо всего прочего, фиг.
10.8 проливает некоторый свет на вопрос, касающийся гидротермального
изменения полевошпатовых пород в зальбандах сульфидных рудных тел. Общая
последовательность зон изменения в сторону от жилы (серицит, каолинит,
хлорит, полевой шпат, биотит) вполне может быть результатом постепенного
уменьшения отношения [K+]/[H+], сопровождаемого
повышением активности Mg2+.
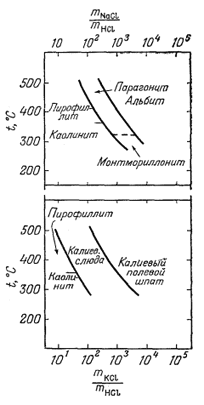
Диаграммы, иллюстрирующие соотношения между силикатами, можно построить для многих температур, если только имеется возможность определить константы равновесия. Хемли и его сотрудники [2], например, исследовали зависимость соотношений между фазами в системах Na2O - Al2O3 - SiO2 - H2O и K2O - Al2O3 - SiO2 - H2O от температуры и величины отношения NaCl к НСl и КСl к НСl в водном растворе; активность кремнезема при данной температуре поддерживалась постоянной благодаря присутствию избытка кварца во всех экспериментах. Фиг. 10.9 заимствована из этой работы. Для реакции, подобной реакции превращения альбита в парагонит,
 |
|
Фиг. 10.9. Некоторые устойчивые соотношения в
системах Na2O - Al2O3 -
SiO2 - H2O и К2О -
Аl2O3 - SiO2 - H2O в
зависимости от температуры и отношений
mNaCl/mHCl и
mKСl/mНСl. |
|
(10.23) |
константа равновесия составит
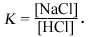
Фактически Хемли с соавторами [2] измеряли отношение mNaCl/mHCl, но вполне вероятно, что оно близко к отношениям [NaCl]/[HCl] или [Nа+]/[Н+] (см. гл. 2). Во всяком случае, анализ фиг. 10.9 показывает, что равновесные соотношения между силикатами можно выражать в виде функции температуры и свойств водного раствора, сосуществующего с этими минералами.
Сопоставление результатов исследования Хемли и его сотрудников [2] и данных, полученных Орвилем [4] по щелочному ионному обмену между паровой и полевошпатовой фазами, позволяет построить изотермические диаграммы для некоторых важных силикатных фаз при высоких температурах, а также выразить соотношения между силикатами в виде функции состава раствора.
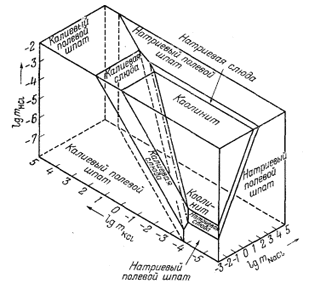
На фиг. 10.10 представлена диаграмма для 300° С и общего давления 15 000 фунт/кв. дюйм (@ 1050 кг/см2).
Она отражает устойчивые соотношения полевых шпатов, слюд и каолинита в зависимости от mNaCl, MKCl и MHCl. Данные, использованные при составлении этой диаграммы, и методика ее построения заслуживают более детального рассмотрения. Обратимся к подробностям построения верхней плоскости диаграммы фиг. 10.10. Эта плоскость отвечает определенной концентрации НСl. В результате экспериментов Хемли с соавторами [2] удалось установить соотношения калиевого полевого шпата, калиевой слюды и каолинита, а также натриевого полевого шпата, натриевой слюды и каолинита в зависимости от величины отношения КСl или NaCl и НСl при данной температуре. Следовательно, если задаться некоторой концентрацией НСl, можно определить такие концентрации KCl или NaCl, при которых различные пары упомянутых выше минералов будут находиться в равновесии. Орвиль [4] вывел отношения КСl к NaCl для случая равновесия между натриевым и калиевым полевыми шпатами в виде функции температуры. Пользуясь его данными, можно определить равновесные соотношения между этими минералами при любой температуре, в частности при интересующей нас температуре 300° С. Теперь мы можем составить уравнения, связывающие твердые фазы с NaClводн и КСlводн, и определить таким образом равновесные границы между минералами. Если эти две серии исходных данных будут взаимно согласовываться, все линии должны сойтись и в результате должна получиться полная диаграмма (устойчивых соотношений) для 300° С (при допущении, что кварц имеется в избытке и что концентрация HCl постоянна и равна 10-2 М). (Одновременно следует предположить, что при 300° С достигается равновесие между натриевым
 |
|
Фиг. 10.10. Примерные фазовые соотношения в системе
Na2O - K2O - Al2O3 -
SiO2 - Н2О при 300° С и давлении 15 000
фунт/кв. дюйм (= 1050
кг/см2); предполагается, что кварц
находится в избытке. |
полевым шпатом и натриевой слюдой, а не между натриевым полевым шпатом и монтмориллонитом. Метастабильное продолжение кривой натриевый полевой шпат - натриевая слюда на фиг. 10.9 должно проходить очень близко к границе натриевый полевой шпат - натриевый монтмориллонит.)
Рассмотрим каждую реакцию отдельно при 300° С, а значения констант равновесия определим по фиг. 10.9:
|
|||||||||||||||||||||
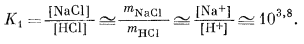 |
|||||||||||||||||||||
| Если mHCl = 10-2, то mNaCl составит 101,8. | (10.24) | ||||||||||||||||||||
|
|||||||||||||||||||||
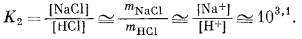 |
|||||||||||||||||||||
| Если mHCl = 10-2, то mNaCl составит 101,1. | (10.25) | ||||||||||||||||||||
|
|||||||||||||||||||||
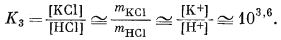 |
|||||||||||||||||||||
| Если mHCl = 10-2, то mKCl составит 101,6. | (10.26) | ||||||||||||||||||||
|
|||||||||||||||||||||
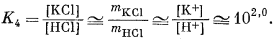 |
|||||||||||||||||||||
| Если mHCl = 10-2, то mKCl будет равно 100. | (10.27) | ||||||||||||||||||||
 |
|
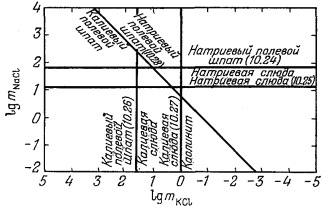
Фиг. 10.11. Экспериментально установленные значения
mKCl и mNaCl для случая
равновесия между различными твердыми фазами (и раствором) при 300° С
и давлении 15 000 фунт/кв. дюйм (~ 1050
кг/см2). |
Полученные значения mNaCl и mKCl под соответствующими номерами показаны на фиг. 10.11. По результатам исследования Орвиля для 300° С находим:
|
||||||||
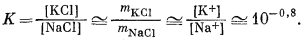 |
(10.28) |
Отсюда следует, что граница между натриевым и калиевым полевыми шпатами на фиг. 10.11 должна подчиняться этому отношению и проходить с наклоном 1:1. Данная линия под своим номером и нанесена на диаграмме.
Далее мы можем определить наклон границы между натриевой и калиевой слюдами, если воспользуемся уравнением
|
||||||||
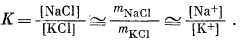 |
(10.29) |
Равновесная граница между этими двумя фазами на фиг. 10.11 должна представлять собой прямую с наклоном 1:1, но ее положение можно определить лишь с помощью анализа других равновесии.
Наконец, наклон границы между калиевой слюдой и натриевым полевым шпатом выводится из уравнения
|
|||||||||||||||||||||||
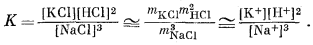 |
(10.30) | ||||||||||||||||||||||
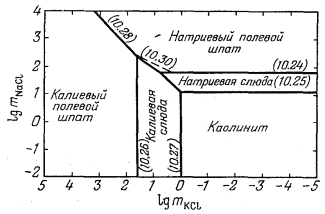
Окончательная диаграмма приведена на фиг. 10.12; метастабильные продолжения линий, проведенные на фиг. 10.11, здесь не показаны. Некоторое несоответствие в использованных данных отражено в несовпадении
 |
|
Фиг. 10.12. Фазовые соотношения в части системы
Na2O - K2O - Al2O3 -
SiO2 - H2O при 300° С и давлении 15 000
фунт/кв. дюйм (~ 1050
кг/см2). |
наклона линии (10.30) с наклоном прямой, рассчитанном по уравнению (штриховая линия). Однако такое несовпадение не превышает точности отсчета значений констант равновесия по фиг. 10.9.
Из вышеизложенного ясно, каким образом использовались экспериментальные данные при построении верхней плоскости фиг. 10.10. Для любого другого сечения, отражающего иные значения mHCl все расчеты будут аналогичны; по совокупности подобных сечений можно построить окончательную блок-диаграмму.
Успешное сопоставление данных Хемли с соавторами [2] с данными Орвиля [4] имеет далеко идущие последствия. Во-первых, оно показывает, что по значениям моляльности растворенных компонентов устанавливаются такие же геометрические соотношения, как и при проведении расчетов по величинам активности. Другими словами, отношения моляльностей НСl, NaCl и КСl почти не отличаются от соответствующих отношений активностей; коэффициенты активности этих солей в лабораторных условиях должны быть одинаковы. Второе, возможно, еще более важное следствие: данные Хемли и его сотрудников были получены в результате экспериментов, при которых твердые вещества содержали только Na или К, тогда как в опытах Орвиля одновременно участвовали натриевый и калиевый полевые шпаты, каждый из которых содержал по нескольку мольных процентов другого. Использованные константы равновесия были выведены при допущении, что активность твердых фаз равна единице, т. е. что каждая такая фаза представлена в ее чистом состоянии. Поправки на величину отклонения активностей от единицы для полевых шпатов в опытах Орвиля были бы исчезающе малы, если бы поведение полевых шпатов как твердых растворов отклонялось от идеального лишь незначительно. Однако ясно; что это не так. Подобный вывод подтверждается всеми данными Орвиля по составу раствора и твердого вещества. Такие же рассуждения в полной мере справедливы и по отношению к слюдам; фактически в присутствии К и Na не происходит образования чистых конечных фаз, которым посвятили свое исследование Хемли и его сотрудники [2].
Следует отметить, что
изменение стандартных свободных энергий для всех реакций между фазами,
показанными на фиг. 10.12, можно рассчитать с точностью до нескольких
десятых килокалорий. Через некоторое время мы будем знать стандартные
свободные энергии образования соединений при повышенных температурах.
Тогда мы сможем строить диаграммы устойчивости, показывающие соотношения
между твердыми веществами и их растворами при высоких температурах, так же
легко, как это мы делаем для условий комнатной температуры. Достаточно
лишь определить величины DF°обр
некоторых важнейших соединений; остальные можно будет вычислить путем
расчета реакций, подобных только что рассмотренным.
Здесь мы представим совсем
немного диаграмм, показывающих устойчивые соотношения между карбонатами и
сульфатами. Для более детального ознакомления с диаграммами этого типа
читателю следует обратиться к сборнику под редакцией Шмитта [5].
Приводимые ниже диаграммы выбраны с таким расчетом, чтобы показать
различные возможные комбинации переменных, используемые при графическом
изображении фазовых соотношений.
Ни в одной из рассмотренных выше систем активность воды не отклонялась заметно от единицы. В системе же Na2O - CO2 - H2O, которая в первом приближении отвечает составу вод некоторых соляных озер, концентрация растворенного материала настолько высока, что активность воды начинает выступать в качестве одного из факторов, влияющих на устойчивость твердых веществ. В данном случае активность воды зависит от отношения РH2O системы к давлению пара чистой жидкой воды при одних и тех же условиях давления и температуры. Это определение относится как к водным растворам, так и к средам, в которых жидкая фаза отсутствует. Активность воды, данная в таком определении, и относительная влажность - синонимы (если только относительная влажность дается в виде отношения, а не в процентном выражении).
К наиболее важным минералам в богатых карбонатами озерах относятся нахколит NaHCO3, трона NaHCO3ЧNa2CO3Ч2H2O, натрон Na2CO3ґ10H2O и термонатрит Na2CO3ЧH2O.
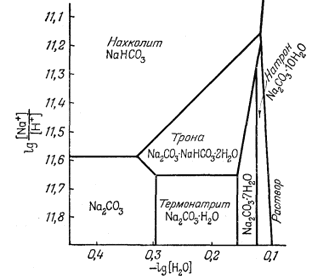
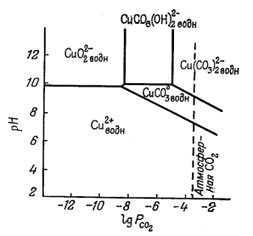
На фиг. 10.13 изображены соотношения между этими компонентами при 25° С, данные в виде функции [H+]/[Na+] и [Н2О]. При постепенной гидратации Na2CO3 в нижней части диаграммы в качестве единственной переменной в константе равновесия выступает активность воды. Например,
Nа2СО3ЧН2Окрист +
6Н2Ожидк = Na2CO3Ч7Н2Окрист,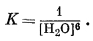
Следовательно, границы между такими гидратами представляют собой вертикальные прямые, независимые от ординаты.
 |
|
Фиг. 10.13. Соотношения между некоторыми фазами в
системе Na2O - CO2 - Н2О при 25° С
и 1 атм, выраженные в виде функции [Н2О] и
[Na+]/[H+]. |
С другой стороны, для реакции перехода от термонатрита к троне
2Na2CO3ЧН2Окрист +
Н+водн =
Na3H(CO3)2Ч2Н2Окрист +
Na+водн,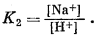
Граница между этими двумя фазами изображается горизонтальной линией, независимой от [H2O].
Для определения границы между тропой и нахколитом следует рассмотреть реакцию
Na3H(CO3)2Ч2Н2Oкрист +
Н+водн = 2NaHCO3 крист +
Na+водн + 3Н2Оводн,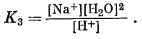
На графике, осями координат которого служат [Na+]/[H+] и lg[Н2О], эта граница будет представлена наклонной линией. Исходя из правила фаз, можно предсказать, что для описания равновесия между этими фазами потребуются только две характеристические переменные. Если в трехкомпонентной системе при постоянных температуре и давлении присутствуют три фазы, то должна существовать инвариантная точка, подобная точке одновременного существования Na2CO3, термонатрита и троны. Если же имеются две фазы, граница между фазами будет прямой линией; при, наличии лишь одной фазы последняя на графике с двумя переменными выразится некоторой площадью.
 |
|
Фиг. 10.14. Часть фазовой диаграммы для системы
Na2O - СО2 - Н2О при 25°С и 1
атм общего давления; в качестве переменных приняты
РH2O и
РCO2. |
Диаграмма, подобная изображенной на фиг. 10.13, полезна для исследователя, желающего оценить влияние подкисления воды содового озера, например в связи с вулканическими эманациями, или же предугадать последствия повышения содержания NaCl. Эта диаграмма будет чрезвычайно полезна и для геохимика, которому при работе в поле необходимо провести непосредственные измерения [Na+] и [Н+] с помощью стеклянных электродов и определить давление пара озерной воды. Он сможет сразу же сказать, находятся ли твердые вещества в осадках данного озера в равновесии с раствором.
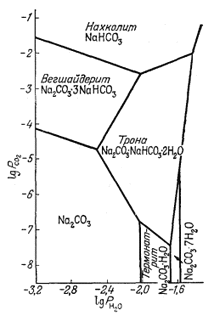
При построении диаграммы
фиг. 10.14 использованы две другие характеристические переменные -
давление водяного пара и давление CO2; эта диаграмма
характеризует часть той же системы, что и фазовая диаграмма фиг. 10.13. На
новой диаграмме показана фаза вегшайдерита, которая при температурах выше
25° С существует метастабильно.
Еще одним примером произвольного выбора характеристических переменных может служить работа Силмена [7] по устойчивым соотношениям между карбонатами и сульфатами меди. Силмена интересовало количество меди, способное растворяться в природных водах, в связи с проблемой геохимических поисков медных месторождений с помощью химического анализа вод. По результатам такого анализа легко найти сум-.марное содержание растворенного СО2(СО2-3 + НСО-3 + H2CO3), а также SO2-4 и рН. Силмен пришел к выводу, что максимальное содержание растворенной меди в речной или озерной воде, вероятно, равновесно по отношению к различным основным сульфатам и карбонатам. Это в свою очередь дало возможность установить такой состав воды, в котором равновесное содержание меди слишком низко, чтобы его можно было использовать с поисковыми целями.
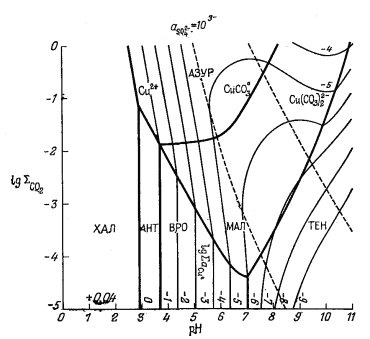
На фиг. 10.15 показана зависимость полей устойчивости окисленных минералов меди от SO2-4 рН и суммы растворенного карбоната. Эта исходная диаграмма нужна лишь для того, чтобы выяснить, какие минералы меди будут выделяться из данной речной или озерной воды. Поскольку Силмену требовалось определить растворимость меди, а не активность иона меди, он измерял фактическую концентрацию растворенной меди в условиях равновесия с различными минералами, а затем распределял сумму растворенной меди по различным компонентам раствора.
 |
 |
|
Фиг. 10.15. Устойчивые соотношения между некоторыми окисленными минералами меди при 25° С, показанные в виде функции определенных свойств речных и озерных вод; по Силмену [5, стр. 119]. |
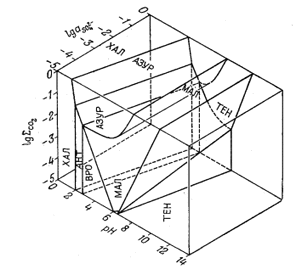
Фиг. 10.16. Распределение растворенных медьсодержащих компонентов при 25° С и 1 атм общего давления, данное в виде функции рН и PCO2 (давление выражено в атмосферах). Построено по данным Шмитта [5, стр. 116]. |
 |
|
Фиг. 10.17. Одно из сечений фиг. 10.15, проведенное
при aSO2-4 =
10-3. |
На фиг. 10.16 представлена диаграмма, построенная Шмиттом [5]. На ней четко показаны поля различных медьсодержащих компонентов, рассмотренных Силменом, и охарактеризована среда их нахождения. На фиг. 10.17 изображено вертикальное сечение диаграммы Силмена (фиг. 10.15) при постоянной активности SO2-4. На поля устойчивости минералов нанесены изолинии активностей различных компонентов раствора, содержащих медь.
Пользуясь диаграммами Силмена, по стандартным анализам воды можно определить, будет ли данный медный минерал равновесен с этой водой, а также найти максимальное содержание меди в растворе, существующем равновесно с этим минералом.
Наконец, они характеризуют
вид и свойства тех растворенных компонентов, которые определяют суммарную
(валовую) растворимость меди.
Рассматриваемые ниже диаграммы с карбонатами кальция и магния приведены не для того, чтобы показать новый вид характеристических переменных, а для демонстрации целесообразности использования диаграмм равновесия при анализе систем с метастабильными фазами. Даже
 |
|
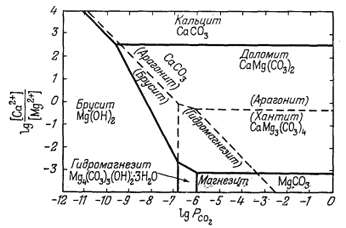
Фиг. 10.18. Соотношения между карбонатами кальция и
магния при 25° С и 1 атм общего давления, выраженные в виде
функции PCO2 (в атмосферах) и
[Ca2+]/[Mg2+]. |
если какая-либо фаза метастабильна по отношению к другой фазе (или к другим фазам), довольно легко устанавливаются равновесные условия между этой фазой и ее средой. Можно, например, измерить растворимость арагонита, достигая величины насыщения (как из разбавленного раствора, так и из пересыщенного). Диаграмма, иллюстрирующая соотношения арагонита с раствором, может рассматриваться как диаграмма равновесия, так как она определяет соотношения твердого вещества и раствора; неравновесная диаграмма описывает взаимоотношения только между твердыми веществами.
Карпентеру [5, стр. 26]
удалось построить интересную диаграмму, показывающую метастабильные и
устойчивые соотношения между карбонатами кальция и магния
(фиг. 10.18). К числу метастабильных фаз относятся арагонит и хантит;
граница между этими двумя фазами и границы между этими и устойчивыми
фазами рассчитывались по величине DF°обр тем же способом, как и для
одних стабильных фаз. Представленная диаграмма помогла Карпентеру
разобраться в парагенетических соотношениях минералов из гипергенных
прожилков района Крестмор в Калифорнии. В составе этих прожилков
установлены арагонит, хантит, брусит, доломит, магнезит, гидромагнезит и
кальцит. Оказалось, что ранние минеральные парагенезисы отвечают
метастабильной диаграмме, изображенной на фиг. 10.18 штриховыми линиями.
По-видимому, в конце концов ранние минералы приходят в равновесие со
средой, достигая фазовых соотношений, показанных на диаграмме сплошными
линиями. Данная диаграмма имеет еще то достоинство, что с ее помощью можно
проиллюстрировать основную геологическую закономерность: "чем древнее
горная порода, тем меньше сведений об условиях ее образования". Обратите
внимание на относительно ограниченный размер (как по ординате, так и по
абсциссе) полей метастабильных фаз по сравнению с размером полей
устойчивых твердых соединений. Время и достаточное количество воды,
просачивающейся, через осадочные породы, приводят к сокращению числа ранее
существовавших минеральных фаз, причем сохраняются только те минералы,
которые обладают широкими пределами устойчивости.
В данной главе основное
внимание обращено на возможность использования самых различных переменных,
выбираемых по желанию исследователя, для характеристики устойчивых
соотношений между минералами. В качестве примера рассмотрены системы с
участием силикатов, карбонатов и сульфатов. На них мы старались показать,
что, кроме Eh, pH и парциального давления, исследователи могут
воспользоваться не только различными комбинациями этих переменных, но и
другими параметрами. В представленных диаграммах в качестве
характеристических параметров использованы активность индивидуального
иона, моляльность солей, активность воды, отношение активности ионов и
температура. Указано также на целесообразность применения диаграмм,
учитывающих не только устойчивые, но и метастабильные фазы.
10.1. Составьте уравнения реакции превращения хантита в доломит таким образом, чтобы константу равновесия можно было выразить через;
a) Mg2+водн и СO2-3
водн,
б) Mg2+водн,
Н+водн, и НСО-3 водн,
в)
Mg2+водн, Н+водн,
Н2жидк и СO2 газ,
г)
Са2+водн, и СO2-3 водн.
Ответ:
а) СаМg3(СО3)4 крист =
CaMg(CO3)2 крист + 2Mg2+водн +
2СО2-3 водн,
б)
СаМg3(СО3)4 крист +
2Н+водн = CaMg(CO3)2 крист +
2Mg2+водн + 2НСО-3 водн
в)
CaMg3(CO3)4 крист +
4Н+водн =
= CaMg(CO3)2
крист + 2Mg2+водн +
2H2Oжидк + 2СO2 газ.
г)
CaMg3(CO3)4 крист +
2Са2+водн + 2СО2-3 водн =
3СаМg(СО3)2 крист.
10.2. При 100° С давление
пара чистой воды составляет 760,0 мм рт. ст., а давление
пара 6 М раствора равно 583,5 мм рт. ст. Какова
активность воды.в растворе NaCl при той же
температуре?
Ответ: а =
0,768.
10.3. Равновесное давление пара
чистой воды при 25° С равно 23,8 мм рт. cт. Найдите приблизительное
значение давления водяного пара для раствора, равновесного по отношению к
Na2CO3Ч10H2Oкрист и
Na2CO3Ч7H2Oкрист (фиг.
10.13).
Ответ:
PH2O @ 18 мм рт.
cт.
10.4. Какова стандартная
свободная энергия реакции
3Н2Ожидк + Na2CO3Ч7H2Oкрист = Na2CO3Ч10Н2Oкрист
при 25° С (пользуйтесь только результатами вычислений из
упражнения 10.3).
Ответ: DF°обр @ 0,5
ккал (на 1 моль 10-гидратной
формы).
10.5. Могут ли гиббсит, каолинит
и кварц прийти к равновесию при 25° С, если этот процесс будет
контролироваться активностью воды в
системе?
Ответ: Нет. Для случая
равновесия в реакции
H4Al2Si2O9 крист + Н2Ожидк = Al2O3Ч3Н2Окрист + 2SiO2 крист кварц
активность воды определяется выражением
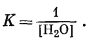
Покажите, что [H2O] характеризуется высоким, практически
недостижимым значением вне зависимости от давления.
1. H e l g e s o n Н.С. Complexing and Hydrothermal Ore
Deposition, New York, Per-gainon, 1964.
2. H e m 1 е у J. J., М е у е г
С., R i с h t е г D. H. U.S. Geol. Surv. Prof. Paper 424-D, 338,
1961.
3. H i l l V. G., Е 1 1 i n g t о n A. C. Econ. Geol., 56, 533,
1961.
4. 0 r v i 1 1 е Р. М. Am. Journ. Sci., 261, 201, 1963.
5. S с
h m i t t H. H. (ed.). Equilibrium Diagrams for Minerals, Cambridge,
Mass., The Geological Club of Harvard, 1962.
6. S i e v e r R. Am.
Mineral., 42, 826, 1957.
7. S i l m a n J.R. Ph. D. thesis, Department
of Geological Sciences, Harvard University, 1958.
S с h m i t t H. H. (ed.). Equilibrium Diagrams for
Minerals, Cambridge, Mass., The Geological Club of Harvard, 1962.
S i l
l e n L.G. Graphic presentation of equilibrium data, ch. 8, in Treatise on
Analytical Chemistry, Part I, I, Kolthoff I. M., Elving P. J. (eds.), New
York, Interscience, 1959.
|
|
|
|
[Содержание] [Глава 9] [Глава 11] |