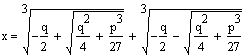1. Иногда вопрос о количестве действительных корней уравнения важен сам по себе, вне зависимости от численного решения уравнения. Как известно, решение кубического уравнения общего вида

сводится введением нового неизвестного к решению так называемого неполного уравнения

т.е. уравнения, в котором коэффициент при x² равен нулю, а при x³ - единице. При этом оказывается, что коэффициенты p и q этого уравнения более информативны, чем коэффициенты a, b, c и d исходного уравнения. Так, именно по коэффициентам неполного уравнения p и q можно не решая уравнения легко сказать, сколько действительных корней оно имеет. Кроме того, p и q имеют простой геометрический смысл. (Анализ зависимости количества корней неполного кубического уравнения дан здесь и здесь.)

Если помимо или независимо от вопроса о количестве действительных корней кубического уравнения нас интересует численное решение уравнения, то один из способов найти все решения – воспользоваться формулой Кардано. Формула Кардано традиционно записывается именно для неполного уравнения, ввиду того, что подобная формула для уравнения общего вида становится чрезвычайно громоздкой:

Несмотря на простоту этой формулы при ее использовании могут возникнуть определенные трудности. В том случае, когда уравнение имеет ровно три действительных решения, для их нахождения по этой формуле нужно, во-первых, уметь извлекать кубический корень из комплексного числа, а во-вторых (и это касается любого случая, а не только когда у уравнения только действительные решения), уметь исключать появление посторонних решений. Второй момент связан с тем, что каждому слагаемому в формуле, как корню третьей степени из комплексного числа, соответствует три комплексных значения, что в общей сложности дает девять комбинаций слагаемых, т.е. девять значений , тогда как всего решений (в любом случае) – ровно три! Иногда формулу сопровождают пояснениями, какие пары значений корня третьей степени следует брать, чтобы найти все решения уравнения без лишних вычислений. Тем не менее, даже хорошо зная какой-либо алгоритм нахождения корней кубического уравнения, перед тем как приступать к решению уравнения нелишне выяснить, сколько корней оно имеет и каково их взаимное расположение, т.е. задаться вопросом, о котором идет речь в начале заметки. Это дополнение к алгоритму поиска решений уравнения делает процесс решения более наглядным, а вычисления более надежными. (Вывод формулы Кардано и комментарий по ее применению приведены здесь.)

2. Здесь показано как MathCAD обрабатывает сумму корней третьей степени из комплексных чисел: результат – только одно число.

3. Здесь приведен пример извлечения корня третьей степени из комплексного числа «вручную». Формула MathCAD дает только одно число; чтобы получить все три значения, нужны дополнительные вычисления.

Линьков Леонид Владимирович

На базовую страницу >>>