Высшая математика

  Если e₁, e₂, ..., e_n — ортонормированный базис n-мерного евклидова пространства.

Если x = x₁e₁ + x₂e₂ + ... + x_ne_n , y = y₁e₁ + y₂e₂ + ... + y_ne_n — разложения векторов x и y по этому базису, то скалярное произведение векторов x и y вычисляется по формуле:

(x, y) = x₁· y₁ + x₂· y₂ + ... + x_n· y_n .

При этом длина вектора, расстояние и угол между векторами вычисляются по формулам:

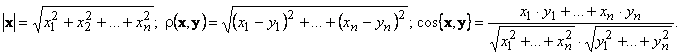
Если x — вектор-столбец координат вектора в ортонормированном базисе, то скалярное произведение скалярное произведение (x, y) векторов x и y можно записать в матричной форме: (x, y) = x·y^T.

Заметим, что если A —квадратная матрица соответствующего размера, то (A·x, y) = x·A^T·y^T.