Высшая математика

    Пусть A — квадратная матрица порядка n:

    Если существует квадратная матрица X той же размерности, что и матрица A,  

    удовлетворяющая соотношениям A·X = X·A = I,  то матрица A называется обратимой,

    а матрица X называется обратной к матрице A и обозначается A⁻¹.

    Здесь I — единичная матрица соответствующей размерности:

A·A⁻¹ = A⁻¹·A = I.

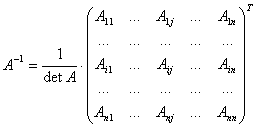
    Всякая невырожденная матрица A имеет единственную обратную матрицу

 

A_ij  — алгебраическое дополнение элемента a_ij  матрицы A.