Элементарная математика

     В тригонометрии углом считают меру поворота подвижного радиус-вектора относительно его начального положения. Приведем необходимые понятия.  Рассмотрим декартову систему координат  Oxy.
Радиус-вектором  точки  M называется вектор, началом которого  является  начало  O системы координат, а концом  – точка  M  (обозначение: 
r = OM). Длиной радиус-вектора OM называется длина отрезка OM     (обозначение:   | r | =  r = | OM|).

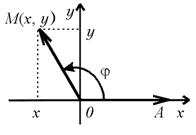
      Будем  вращать радиус-вектор   OM  вокруг точки  O. Положение   OA этого вектора, которое совпадает с положительным направлением оси   Ox,  назовем  начальным  положением  радиус-вектора  OM,  а сам радиус-вектор
OM  –   подвижным  радиус-вектором.
Говорят, что вектор  OM образует со своим начальным положением  OA угол
,

если вектор  OM,  начиная от положения  OA,  сделав  n  полных оборотов против  часовой стрелки,  повернулся еще на угол в     градусов в том же направлении.
Если же вектор  OM,  начиная от своего начального положения  OA, сделал  n полных оборотов  по  часовой стрелке и повернулся еще на угол в   градусов  в том же направлении, то говорят, что угол между вектором  OM  и его начальным положением  OA   равен 

    Таким образом, при вращении подвижного радиус-вектора  OM   против часовой стрелки получаются положительные углы, а при вращении по  часовой  стрелке –  отрицательные углы.