Элементарная математика

    Рассмотрим  тригонометрические  уравнения  вида

                                                       (1)

 где   R (u, v)  –  дробно-рациональная  функция  от   переменных  u, v.
Общий метод решения таких уравнений основан на замене переменной

                                     (2)

      Используя  выражения  тригонометрических  функций  через  тангенс
половинного  аргумента,  будем  иметь

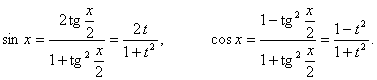
 При  этом  уравнение  (1)  преобразуется  к  виду

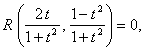                                                  (3)

которое  является  дробно-рациональным  уравнением  относительно  t.  Оно сводится  (после  умножения  на  общий  знаменатель)  к  многочленному уравнению.  Найдя  корни   

уравнения  (3),  получим  простейшие  уравнения 

Решив  эти  уравнения,  найдем  корни  исходного  уравнения.
Замена  (2)  сужает  ОДЗ  исходного  уравнения  (1),  так  как  функция
   не  имеет  смысла  при
                             (4)

     Поэтому,  при  решении  уравнения  (1)  с  помощью  универсальной подстановки  (2)  можно  потерять  корни  (4).  Чтобы  этого  не  произошло, необходимо  с  самого  начала  проверить,  будут  ли  значения  (4)  переменной  x   корнями  уравнения  (1),  а  затем,  считая,  что  

применить  подстановку  (2).

       Универсальная  подстановка  (2)  может  привести  к  громоздким  выкладкам.  Поэтому,  по  возможности,  следует  использовать  другие  методы  решения  уравнения  (1). 

ПРИМЕР