| ОГЛАВЛЕНИЕ | ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ | ПОЛЕЗНЫЕ ССЫЛКИ |
Элементарная математика
Радиус вектор точки. Угол в тригонометрии
Тригонометрические функции и их свойства
Определение тригонометрических функций
Значения тригонометрических функций
Основные свойства тригонометрических функций
Свойства функции y = sin x и ее график
Свойства функции y = cos x и ее график
Основные формулы тригонометрии
Основные тригонометрические тождества
Тригонометрические функции суммы и разности углов (формулы сложения)
Тригонометрические функции двойных и тройных углов
Формулы понижения степени (тригонометрические функции половинных углов)
Преобразование суммы или разности тригонометрических функций в произведение
Преобразование произведений тригонометрических функций в сумму или разность
Выражение тригонометрических функций через тангенс половинного аргумента
Обратные тригонометрические функции (аркфункции) и их свойства
Значения обратных тригонометрических функций часто встречающихся углов
Решение тригонометрических уравнений
Понятие тригонометрического уравнения
Простейшие тригонометрические уравнения и формулы их решений
Тригонометрические уравнения, содержащие тригонометрические функции с одним и тем же аргументом
Тригонометрические уравнения, рациональные относительно sin x и cos x. Универсальная подстановка
Тригонометрические уравнения, содержащие тригонометрические функции с разными аргументами
Уравнения, левая часть которых разлагается на множители, а правая равна нулю
Простейшие тригонометрические неравенства
Задача. Решить уравнение sin x – 3 cos x = 3.
Решение. Воспользуемся универсальной подстановкой 
. Сначала необходимо проверить, будут ли значения
(1)
при которых функция 
не имеет смысла, корнями нашего уравнения:
Итак, значения (1) переменной x обращают данное уравнение в верное числовое равенство, а значит являются его корнями.
Считая, что
применим универсальную подстановку 
. Используя соотношения
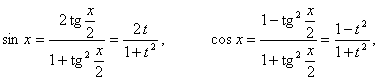
приводим данное уравнение к виду
