Элементарная математика

          Рассмотрим  уравнение  вида  

                                                     (1)

где  a, b  и  c–  известные  числа.  Для  его  решения  часто  используют  метод, называемый   методом  введения  вспомогательного  аргумента.  Суть его заключается  в  следующем.  Поскольку  уравнение  (1)  имеет  смысл рассматривать  лишь  при  условии,  что  a  и   b  не обращаются  одновременно в нуль,  то  можно  разделить  обе  его  части  на   .  В  результате получим  равносильное  уравнение

Введем  угол   ,  для которого выполняются равенства

                                          (2)

такой угол существует, так как  справедливо  равенство

Тогда  последнее  уравнение  примет  вид

      Если  

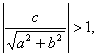
то  полученное  уравнение  (а  значит  и  уравнение  (1))  решений  не  имеет;  если же

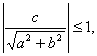
то  полученное  уравнение  является  простейшим  тригонометрическим  уравнением  и  имеет  решения

Подчеркнем  еще  раз,  что  здесь    находится  с   помощью соотношений (2).

ПРИМЕР