Элементарная математика

    Задача.  Решить  уравнение

    Решение.  ОДЗ  уравнения  определяется  условием

Так как

то  данное  уравнение  можно  представить  в  виде

Поскольку
 
 
то  левая  и  правая  части  последнего  уравнения  допускают  такие  оценки:

Отсюда  следует,  что  в  ОДЗ  данное  уравнение  равносильно  следующей
системе  уравнений  (см. утверждение 2):

Так  как

то, применяя   утверждение 1  к  первому  уравнению  полученной  системы, сводим  ее  к  следующей  системе  уравнений:

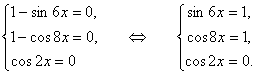                                    (1)

     Сначала  найдем  решения  третьего  уравнения  системы  (1):

Выясним  теперь,  при  каких  целых  значениях   r   найденные  решения
третьего  уравнения   системы  (1)  удовлетворяют  также  первому  и  второму
уравнениям  этой  системы.   С  этой  целью  представим  целое  число   r   по модулю  2:

и  разобъем  полученную  серию  решений  на  две  серии:

                                 (2)

    Подставим  первую  серию  из  (2)  в  первое  уравнение  системы  (1):

Следовательно,  первая  серия  из  (2)  не  удовлетворяет  первому  уравнению системы  (1),  а  значит  она  не  принадлежит  множеству  ее  решений.

    Подставим вторую серию из (2) в первое уравнение системы (1):

Итак,  вторая  серия  из  (2)  удовлетворяет  первому  уравнениюм системы  (1).        
Подставим  теперь  вторую  серию  из  (2)   во  второе уравнение  системы  (1):

Следовательно,  вторая  серия  из  (2)  удовлетворяет  и  второму  уравнению системы  (1).

     Таким  образом,  вторая  серия  решений  из  (2)  удовлетворяет  всем  трем уравнениям  системы  (1), а  значит  она  и  является  множеством  решений  как системы  (1),  так  и  равносильного  ей  исходного  уравнения.  Отметим,  что   все  найденные  решения  принадлежат  ОДЗ  данного  уравнения.

НАЗАД