| ОГЛАВЛЕНИЕ | ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ | ПОЛЕЗНЫЕ ССЫЛКИ |
Элементарная математика
Задача. Решить неравенство tg (2x – ![]() / 5) > 2.
/ 5) > 2.
Решение. Сделав замену 2x – ![]() / 5 = t, получаем неравенство tg t > 2. Вначале решаем его на интервале (–
/ 5 = t, получаем неравенство tg t > 2. Вначале решаем его на интервале (– ![]() / 2,
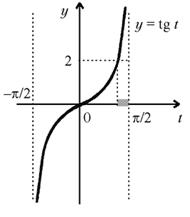
/ 2, ![]() / 2) с помощью графика функции y = tg t (см. рисунок).
/ 2) с помощью графика функции y = tg t (см. рисунок).
Проведя прямую y = 2, видим, что на интервале (– ![]() / 2,
/ 2, ![]() / 2)
/ 2)
неравенству tg t > 2 удовлетворяют числа из интервала ( arctg 2, ![]() / 2), отмеченного на рисунке штриховкой. Поскольку функция y = tg x имеет период T =
/ 2), отмеченного на рисунке штриховкой. Поскольку функция y = tg x имеет период T = ![]() , множеством всех решений этого неравенства будет множество
, множеством всех решений этого неравенства будет множество
![]()
Возвращаясь с помощью формулы t = 2x – ![]() / 5 к переменной x, получаем
/ 5 к переменной x, получаем
множество всех решений исходного неравенства:
![]()
![]()


 Тригонометрия
Тригонометрия Понятие угла в тригонометрии
Понятие угла в тригонометрии