| ОГЛАВЛЕНИЕ | ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ | ПОЛЕЗНЫЕ ССЫЛКИ |
Элементарная математика
Радиус вектор точки. Угол в тригонометрии
Тригонометрические функции и их свойства
Определение тригонометрических функций
Значения тригонометрических функций
Основные свойства тригонометрических функций
Свойства функции y = sin x и ее график
Свойства функции y = cos x и ее график
Основные формулы тригонометрии
Основные тригонометрические тождества
Тригонометрические функции суммы и разности углов (формулы сложения)
Тригонометрические функции двойных и тройных углов
Формулы понижения степени (тригонометрические функции половинных углов)
Преобразование суммы или разности тригонометрических функций в произведение
Преобразование произведений тригонометрических функций в сумму или разность
Выражение тригонометрических функций через тангенс половинного аргумента
Обратные тригонометрические функции (аркфункции) и их свойства
Значения обратных тригонометрических функций часто встречающихся углов
Решение тригонометрических уравнений
Понятие тригонометрического уравнения
Простейшие тригонометрические уравнения и формулы их решений
Тригонометрические уравнения, содержащие тригонометрические функции с одним и тем же аргументом
Тригонометрические уравнения, рациональные относительно sin x и cos x. Универсальная подстановка
Тригонометрические уравнения, содержащие тригонометрические функции с разными аргументами
Уравнения, левая часть которых разлагается на множители, а правая равна нулю
Простейшие тригонометрические неравенства
Задача. Решить неравенство sin x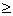 
0,5.
Решение. Так как наименьший период функции y = sin x равен 2
, то, согласно общей схеме, сначала решаем данное неравенство на промежутке [0, 2
). На тригонометрическом круге отмечаем концы радиус-векторов, ординаты которых равны 0,5 (см. рисунок). Таких радиус-векторов два. Один образует с положительным направлением оси Ox угол 
/ 6, а другой – угол 5
/ 6 (cинус каждого из этих углов равен 0,5).
Данное в условии задачи неравенство выполняется для тех углов x, для каждого из которых конец подвижного радиус-вектора, образующего с
положительным направлением оси Ox угол x, находится на верхней дуге, заключенной между 
/ 6 и 5
/ 6 , т.е. если
Принимая во внимание, что функция y = sin x имеет период
T = 2
, получаем множество всех решений данного неравенства:
