| ОГЛАВЛЕНИЕ | ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ | ПОЛЕЗНЫЕ ССЫЛКИ |
Высшая математика
Число λ = 0 является собственным значением матрицы A:
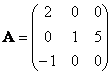
Найдём собственный вектор матрицы, соответствующий собственному значению λ = 0 — то есть найдём нетривиальное решение однородной системы линейных уравнений (A − 0 ·E)·x = 0, x ≠0 :

Действительно, e1 = (0, 5, −1) — собственный вектор, отвечающий собственному значению λ = 0:
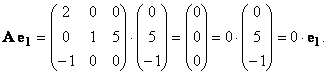
Аналогично, для собственных значений λ = 2 и λ = 1 и соответствующих собственных векторов, имеем:

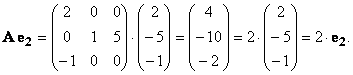




 Линейная алгебра
Линейная алгебра Матрицы
Матрицы