МЕТОД ГАУССА ПРИВЕДЕНИЕ ЛИНЕЙНОЙ СИСТЕМЫ К КАНОНИЧЕСКОМУ ВИДУ

 
ОГЛАВЛЕНИЕ ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ ПОЛЕЗНЫЕ ССЫЛКИ

Высшая математика

Линейная алгебра

Матрицы и определители

Матрицы

Матрицы

Линейные операции с матрицами

Определитель матрицы

Умножение матриц

Обратная матрица

Элементарные преобразования матрицы

Ранг матрицы

Многочлен от матрицы

Нормы матрицы

Определители

Определители

Свойства определителей

Миноры и алгебраические дополнения

Критерий равенства нулю определителя

Вычисление определителей

Правило Крамера

Линейные пространства

Определение линейного пространства

Пространство арифметических векторов Rn

Линейная зависимость и линейная независимость системы векторов

Свойства линейно зависимых и линейно независимых систем векторов

Критерий линейной зависимости системы векторов линейного пространства

Базис линейного пространства

Размерность линейного пространства

Координаты вектора линейного пространства в заданном базисе

Преобразование координат вектора при изменении базиса

Линейные подпространства

Изоморфные линейные пространства

Евклидовы пространства

Определение евклидова пространства

Свойства скалярного произведения

Неравенство Коши-Буняковского

Измерения в линейном пространстве

Ортонормированные системы векторов

Ортонормированный базис

Скалярное произведение в координатах

Полезные соотношения

Ортогональные подпространства

Ортогональные матрицы

Линейные операторы

Определение линейного оператора

Действия с операторами

Матрица линейного оператора

Собственные значения и собственные векторы линейного оператора

Свойства собственных векторов линейного оператора

Характеристический многочлен

Системы линейных уравнений

Основные понятия

Элементарные преобразования линейной системы

Критерий совместности линейной системы

Свойства решений линейной системы

Метод Гаусса приведения системы к каноническому виду

Нетривиальная совместность однородной линейной системы

Фундаментальная система решений

Структура общего решения однородной линейной системы

Структура общего решения неоднородной линейной системы

Квадратичные формы

Билинейная форма

Матрица билинейной формы

Представление билинейной формы в паре базисов

Квадратичная форма

Матрица квадратичной формы

Закон инерции квадратичных форм

Знакоопределённые матрицы

Положительно определённая матрица

Свойства положительно определённых матриц

Критерий положительной определённости матрицы

Квадратный корень из матрицы

Численные методы линейной алгебры

Метод Гаусса решения системы линейных алгебраических уравнений

Метод Гаусса с частичным выбором ведущего элемента

Метод Гаусса с выбором ведущего элемента

Итерационные методы решения системы линейных алгебраических уравнений

Метод простых итераций

Метод Зейделя

Метод релаксации

Обусловленность задачи решения системы линейных алгебраических уравнений

Метод квадратного корня

Метод прогонки

QR-разложение матрицы

Сингулярное разложение матрицы

Степенной метод вычисления наибольшего собственного значения

Метод обратных итераций

Любая система линейных алгебраических уравнений с помощью элементарных преобразований может быть приведена к каноническому виду:

Система линейных уравнений, записанная в каноническом виде, совместна, очевидно, тогда и только тогда, когда b'r+1 = 0, b'r+2 = 0, ..., b'm−1 = 0, b'm = 0.

Общее решение линейной системы, записанной в каноническом виде, очевидно, определяется формулами:

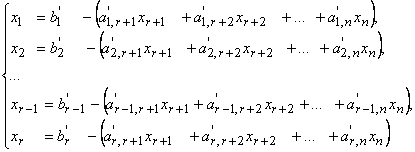
Переменные xr+1 , xr+2 , ..., xm−1, xm могут принимать произвольные значения.

Переменные xr+1 , xr+2 , ..., xm−1, xm называются свободными переменными.

Пременные x1 , x2 , ..., xr−1, xr называются базисными переменными.

Подробнее Примеры  
© МЭИ (ТУ) 2007