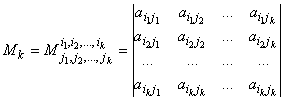| ОГЛАВЛЕНИЕ | ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ | ПОЛЕЗНЫЕ ССЫЛКИ |
Высшая математика
Рассмотрим матрицу A:

Вычеркнем из матрицы k строк с номерами i1, i2, ..., ik и k столбцов, с номерами j1, j2, ..., jk.
Элементы, расположенные на пересечении вычеркнутых строк, образуют определиитель,
который называется минором порядка k. Его обозначают Mk:
Минор, образованный оставшимися элементами называется дополнительным минором
минора Mk и обозначают Mk'.
Алгебраическим дополнением Ak минора Mk называется число, равное дополнительному
минору Mk', умноженному на (−1) в степени, равной сумме номеров вычеркнутыж строк и
столбцов:
Если вычеркнуты одна строка и один столбец, то соответствующие миноры и алгебраические
дополнения называют минорами и алгебраическими дополнениями элемента.
Определитель равен сумме произведений элементов любой строки или любого столбца на их
алгебраические дополнения:
Минор, расположенный в первых k строках и k столбцах, называется угловым минором.
| Подробнее | Примеры | Решить свою задачу |


 Линейная алгебра
Линейная алгебра Матрицы
Матрицы