| ОГЛАВЛЕНИЕ | ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ | ПОЛЕЗНЫЕ ССЫЛКИ |
Высшая математика
Миноры и алгебраические дополнения
Определение линейного пространства
Пространство арифметических векторов Rn
Линейная зависимость и линейная независимость системы векторов
Свойства линейно зависимых и линейно независимых систем векторов
Критерий линейной зависимости системы векторов линейного пространства
Размерность линейного пространства
Координаты вектора линейного пространства в заданном базисе
Определение евклидова пространства
Свойства скалярного произведения
Измерения в линейном пространстве
Ортонормированные системы векторов
Определение линейного оператора
Собственные значения и собственные векторы линейного оператора
Элементарные преобразования линейной системы
Критерий совместности линейной системы
Свойства решений линейной системы
Метод Гаусса приведения системы к каноническому виду
Нетривиальная совместность однородной линейной системы
Фундаментальная система решений
Положительно определённая матрица
Свойства положительно определённых матриц
Численные методы линейной алгебры
Метод Гаусса решения системы линейных алгебраических уравнений
Итерационные методы решения системы линейных алгебраических уравнений
Обусловленность задачи решения системы линейных алгебраических уравнений
Сингулярное разложение матрицы
Степенной метод вычисления наибольшего собственного значения
Множество квадратных матриц размерности 2, с определенными для них операциями сложения и умножения на число — линейное пространство, обозначим его MSQ4.
Рассмотрим упорядоченную линейно независимую систему E1, E2, E3, E4 элементов (векторов) пространства MSQ4 и произвольную матрицу X:
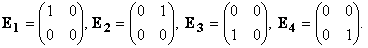
Из приведенного равенств следует, любая квадратная матрица размерности 2 — элемент MSQ4 , может быть представлена разложением по системе векторов E1, E2, E3, E4:
X = x11·E1 +x12·E2 +x21·E3 +x22·E4.
Следовательно система E1, E2, E3, E4 образует базис пространства MSQ4 .
