| ОГЛАВЛЕНИЕ | ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ | ПОЛЕЗНЫЕ ССЫЛКИ |
Высшая математика
Миноры и алгебраические дополнения
Определение линейного пространства
Пространство арифметических векторов Rn
Линейная зависимость и линейная независимость системы векторов
Свойства линейно зависимых и линейно независимых систем векторов
Критерий линейной зависимости системы векторов линейного пространства
Размерность линейного пространства
Координаты вектора линейного пространства в заданном базисе
Определение евклидова пространства
Свойства скалярного произведения
Измерения в линейном пространстве
Ортонормированные системы векторов
Определение линейного оператора
Собственные значения и собственные векторы линейного оператора
Элементарные преобразования линейной системы
Критерий совместности линейной системы
Свойства решений линейной системы
Метод Гаусса приведения системы к каноническому виду
Нетривиальная совместность однородной линейной системы
Фундаментальная система решений
Положительно определённая матрица
Свойства положительно определённых матриц
Численные методы линейной алгебры
Метод Гаусса решения системы линейных алгебраических уравнений
Итерационные методы решения системы линейных алгебраических уравнений
Обусловленность задачи решения системы линейных алгебраических уравнений
Сингулярное разложение матрицы
Степенной метод вычисления наибольшего собственного значения
Совокупность уравнений
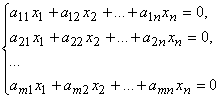
относительна неизвестных x1, x2, ..., xn-1, xn называется однородной системой линейных алгебраических уравнений.
Числа aij — коэффициенты системы, i = 1, 2, ..., m; j = 1, 2, ..., n.
Совокупность значений неизвестных x1, x2, ..., xn-1, xn , удовлетворяющая всем уравнениям системы, называется решением системы.
Однородная система линейных уравнений может быть записана в матричной форме A·x = 0.
Однородная система всегда совместна, поскольку имеет нулевое (тривиальное) решение x = 0:
x1 = 0, x2 = 0, ..., xn-1 = 0, xn = 0.
Если однородная система имеет неулевое решение, она называется нетривиально совместной.