Высшая математика

Неоднородная система линейных уравнений

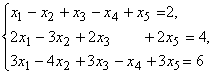
с помощью элементарных преобразований может быть приведена к каноническому виду

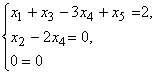
положив значения свободных переменных x₃, x₄ и x₅ равными нулю, получим частное решение неоднородной системы: x₁= 2, x₂ = 0, x₃= 0, x₄ = 0, x₅ = 0.

Приведенная однородная система приводится, соответственно, к каноническому виду

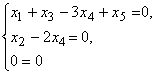
Её общее решение вычисляется по формулам

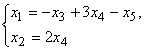
и может быть записано в виде

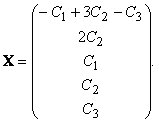
Тогда общее решение неоднородной системы линейных уравнений, равное сумме общего решения приведенной однородной системы и любого частного решения неоднородной системы, имеет вид:

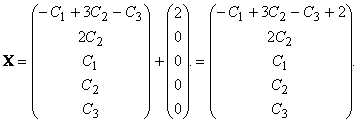
Здесь С₁, С₂, С₃ — произвольные константы.

Правильность решения легко проверить, умножив справа матрицу системы на общее решение: