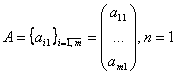| ОГЛАВЛЕНИЕ | ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ | ПОЛЕЗНЫЕ ССЫЛКИ |
Высшая математика
Миноры и алгебраические дополнения
Определение линейного пространства
Пространство арифметических векторов Rn
Линейная зависимость и линейная независимость системы векторов
Свойства линейно зависимых и линейно независимых систем векторов
Критерий линейной зависимости системы векторов линейного пространства
Размерность линейного пространства
Координаты вектора линейного пространства в заданном базисе
Определение евклидова пространства
Свойства скалярного произведения
Измерения в линейном пространстве
Ортонормированные системы векторов
Определение линейного оператора
Собственные значения и собственные векторы линейного оператора
Элементарные преобразования линейной системы
Критерий совместности линейной системы
Свойства решений линейной системы
Метод Гаусса приведения системы к каноническому виду
Нетривиальная совместность однородной линейной системы
Фундаментальная система решений
Положительно определённая матрица
Свойства положительно определённых матриц
Численные методы линейной алгебры
Метод Гаусса решения системы линейных алгебраических уравнений
Итерационные методы решения системы линейных алгебраических уравнений
Обусловленность задачи решения системы линейных алгебраических уравнений
Сингулярное разложение матрицы
Степенной метод вычисления наибольшего собственного значения
Элементы ai1, ai2, ..., ain образуют i-ю строку матрицы A, Ai = {ai1, ai2, ..., ain }.
Элементы a1j, a2j, ..., amj образуют j-й столбец матрицы A,
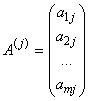
Элементы a11, a22, ..., ann квадратной матрицы A называют диагональными элементами,
они образуют главную диагональ {a11, a22, ..., ann}матрицы A.
Сумма диагональных элементов матрицы называется следом матрицы.
След матрицы: trA = a11+ a22+ ...+ ann.
Квадратная матрица — матрица, у которой одинаковое число строк и столбцов:
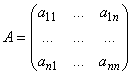
Верхняя треугольная матрица — квадратная матрица, у которой все элементы, расположенные ниже
диагонали — нули:
Нижняя треугольная матрица — квадратная матрица, у которой все элементы, расположенные
выше диагонали — нули:
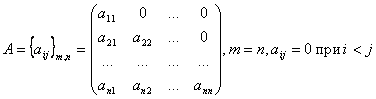
Матрица-столбец — матрица размера n×1:
Матрица-строка — матрица размера 1×n:
Диагональная матрица — квадратная матрица, у которой все внедиагональные элементы равны нулю:
Единичная матрица — диагональная матрица, у которой все диагональные элементы равны единице:
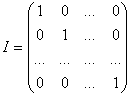
Нулевая матрица — матрица, все элементы которой равны нулю:
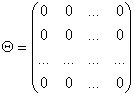
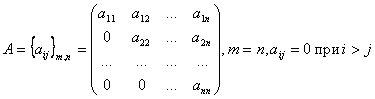
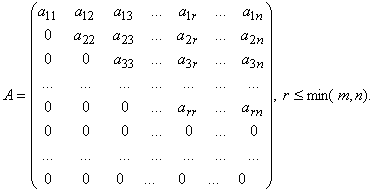
Ступенчатая матрица — матрица, имеющая m строк, у которой первые r диагональных элементов ненулевые, r ≤ m, а элементы, лежащие ниже диагонали и элементы последних m − r строк равны нулю:
| Примеры |