| ОГЛАВЛЕНИЕ | ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ | ПОЛЕЗНЫЕ ССЫЛКИ |
Высшая математика
Для того, чтобы матрица A была обратима, необходимо и достаточно, чтобы det A ≠ 0.
Обратная матрица единственна.
Свойства обратной матрицы (справедливы для любых невырожденных матриц):
• (A·B)−1 = B−1·A−1;
• (A−1)−1= A;
• I −1= I;
• det (A−1) = (det A)−1;
• A·A−1·A = A;
• матрица, обратная к диагональной матрице — диагональная матрица;
• матрица, обратная к треугольной матрице — треугольная матрица;
• матрица, обратная к симметричной матрице — симметричная матрица.
Порядок операций при вычислении обратной матрицы:
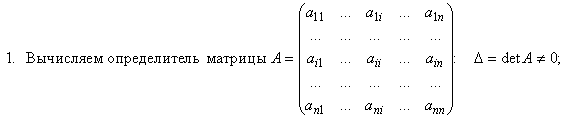

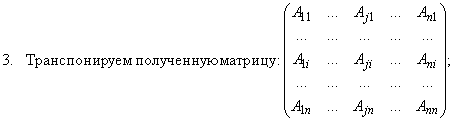
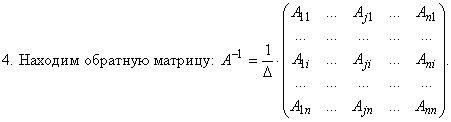
| Примеры | Решить свою задачу |


 Линейная алгебра
Линейная алгебра Матрицы
Матрицы