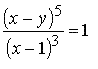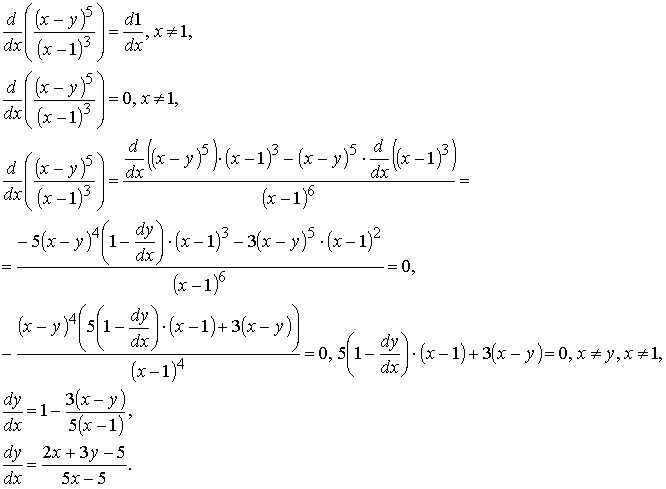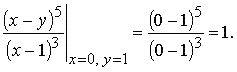| ОГЛАВЛЕНИЕ | ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ | ПОЛЕЗНЫЕ ССЫЛКИ |
Равенство
определяет при всех x ≠ 1 частный интеграл задачи Коши
Действительно.
Продифференцировав равенство для частного интеграла по x и вычислив производную искомого решения y(x) по x, получим тождественное равенство, справедливое при всех x ≠ 1:
Условия Коши тоже, очевидно, выполнены:
| Вернуться | Решить свою задачу |


 Обыкновенные дифференциальные уравнения и системы
Обыкновенные дифференциальные уравнения и системы Обыкновенные дифференциальные уравнения. Основные понятия
Обыкновенные дифференциальные уравнения. Основные понятия