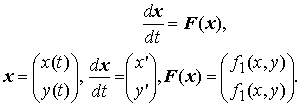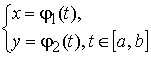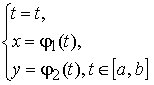| ОГЛАВЛЕНИЕ | ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ | ПОЛЕЗНЫЕ ССЫЛКИ |
Высшая математика
Обыкновенные дифференциальные уравнения и системы
Обыкновенные дифференциальные уравнения. Основные понятия
Связь ОДУ высших порядков и систем ОДУ
ОДУ 1-го порядка. Методы решения
Дифференциальные уравнения 1-го порядка. Основные понятия
Уравнения с разделяющимися переменными
Однородные уравнения 1-го порядка
Уравнения, приводящиеся к однородным
ОДУ 1-го порядка. Поведение решений
Теорема существования и единственности решения задачи Коши
Уравнения 1-го порядка. Поле направлений
Автономные уравнения 1-го порядка
ОДУ высших порядков. Понижение порядка
Понижение порядка ОДУ. Введение
Уравнения, не содержащие независимой переменной
Линейные ОДУ n-го порядка. Введение
Свойства решений линейного уравнения. Принцип суперпозиции
Существование и единственность решения задачи Коши
Линейные уравнения второго порядка. Гармонические колебания
Линейная зависимость и линейная независимость системы функций
Линейная зависимость и линейная независимость системы функций
Исследование линейной независимости системы функций
Линейная независимость решений линейного дифференциального уравнения
Структура решения линейного ОДУ n-го порядка
Фундаментальная система решений однородного линейного дифференциального уравнения
Структура общего решения линейного однородного уравнения
Структура общего решения линейного неоднородного уравнения
Метод вариации произвольных постоянных отыскания частного решения
Линейные ОДУ с постоянными коэффициентами
Решение однородного уравнения с постоянными коэффициентами
Метод подбора построения частного решания неоднородного уравнения
Системы дифференциальных уравнений
Системы обыкновенных дифференциальных уравнений. Основные понятия
Фазовое пространство Фазовые траектории
Существование и единственность решения задачи Коши
Интегрирование систем дифференциальных уравнений методом исключения
Линейные системы OДУ. Структура решения
Линейные системы ОДУ. Основные понятия
Фундаментальная матрица решений однородной линейной системы дифференциальных уравнений
Структура общего решения однородной линейной системы дифференциальных уравнений
Структура общего решения неоднородной линейной системы дифференциальных уравнений
Системы ОДУ. Поведение решений
Устойчивость решений систем дифференциальных уравнений
Устойчивость и асимптотическая устойчивость по Ляпунову
Устойчивость положения равновесия линейных систем ОДУ
Устойчивость точек покоя нелинейных систем по линейному приближению
Неустойчивость по линейному приближению точек покоя нелинейных систем
Автономные системы дифференциальных уравнений
Автономные системы. Основные понятия
Фазовая плоскость, фазовые кривые, фазовый портрет автономной системы 2-го порядка
Векторное поле автономной системы 2-го порядка
Точки покоя линейной автономной системы 2-го порядка с постоянными коэффициентами
Рассмотрим автономную систему второго порядка
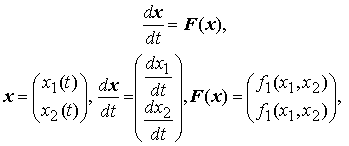
для которой справедлива теорема существования и единственности решения задачи Коши.
При описании интегральных кривых, фазовых траекторий и фазовой плоскости автономной системы 2 –го порядка привычнее вместо переменных (x1,x2) использовать переменные (x,y) В дальнейшем будем записывать автономные системы 2 –го порядка в виде:
Пусть x = φ(t) — решение автономной системы, определенное на отрезке [a, b]. Множество точек x = φ(t) , t ∈ [a, b] — кривая в пространстве Rx,y2 — фазовая траектория системы, а пространство Rx,y2 — фазовая плоскость автономной системы.
Точка a называется положением равновесия (точкой покоя ) автономной системы, если F(a) = 0 .
Равенство x = φ(t) , t ∈ [a,b] , или, что то же самое,
— параметрические уравнения фазовой траектории.
Интегральная кривая системы изображается в 3-х мерном пространстве Rx,y, t2 . Она задается уравнением
Соответствующая фазовая траектория — проекция интегральной кривой на фазовую плоскость.
Изобразив на фазовой плоскости несколько фазовых траекторий так, чтобы можно было убедительно предсказать поведение фазовой траектории, проходящей через любую точку фазовой плоскости (некоторой области фазовой плоскости) получим фазовый портрет автономной системы.
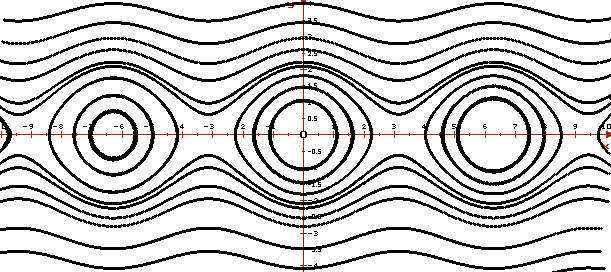
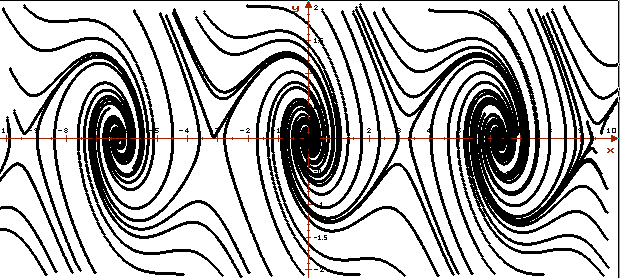
На рисунке приведено изображение фазовых портретов двух автономных систем. Видно, что траектории представленных систем ведут себя по-разному.
На верхнем рисунке приведен фазовый портрет системы, описывающей колебания математического маятника "без трения", на нижнем — колебания математического маятника "с трением".
