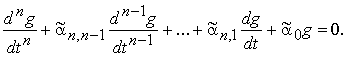| ОГЛАВЛЕНИЕ | ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ | ПОЛЕЗНЫЕ ССЫЛКИ |
Высшая математика
Обыкновенные дифференциальные уравнения и системы
Обыкновенные дифференциальные уравнения. Основные понятия
Связь ОДУ высших порядков и систем ОДУ
ОДУ высших порядков. Понижение порядка
Линейная зависимость и линейная независимость системы функций
Структура решения линейного ОДУ n-го порядка
Линейные ОДУ с постоянными коэффициентами
Решение однородного уравнения с постоянными коэффициентами
Метод подбора построения частного решания неоднородного уравнения
Уравнением Эйлера называется однородное дифференциальное уравнение вида
xny(n) + an-1xn-1y(n - 1) + ... + a1xy' + a0y = 0.
Коэффициенты an-1, ... , a1, a0 — постоянные десйствительные числа.
Если функция y(x) — решение уравнения Эйлера, то функция Cy(x) тоже является решением уравнения.
Уравнение Эйлера заменой x = et сводится к однородному линейному уравнению с постоянными коэффициентами.
Выполним замену x = et, перейдём к новой переменной t = ln x :
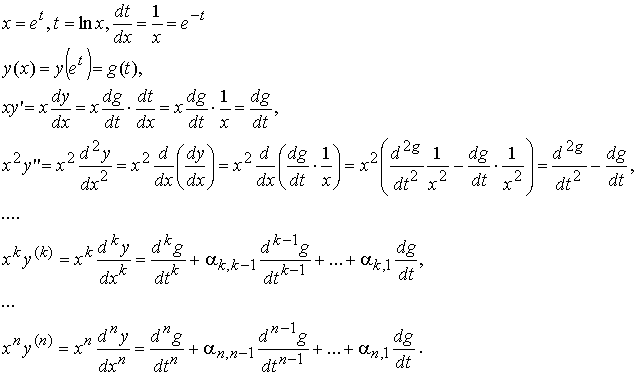
Здесь αij — коэффициенты, которые легко вычисляются при последовательном дифференцировании.
После подстановки в уравнение имеем:
Решим это однородное линейное уравнение с постоянными коэффициентами — его общее решение g = g(t,C1, C2, ... ,Cn). Вернувшись к переменной x, получим общее решение уравнения Эйлера: y(x,C1, C2, ... ,Cn) = g(lnx,C1, C2, ... ,Cn).
| Примеры |