| ОГЛАВЛЕНИЕ | ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ | ПОЛЕЗНЫЕ ССЫЛКИ |
Высшая математика
Обыкновенные дифференциальные уравнения и системы
Обыкновенные дифференциальные уравнения. Основные понятия
Связь ОДУ высших порядков и систем ОДУ
ОДУ 1-го порядка. Методы решения
Дифференциальные уравнения 1-го порядка. Основные понятия
Уравнения с разделяющимися переменными
Однородные уравнения 1-го порядка
Уравнения, приводящиеся к однородным
ОДУ 1-го порядка. Поведение решений
Теорема существования и единственности решения задачи Коши
Уравнения 1-го порядка. Поле направлений
Автономные уравнения 1-го порядка
ОДУ высших порядков. Понижение порядка
Понижение порядка ОДУ. Введение
Уравнения, не содержащие независимой переменной
Линейные ОДУ n-го порядка. Введение
Свойства решений линейного уравнения. Принцип суперпозиции
Существование и единственность решения задачи Коши
Линейные уравнения второго порядка. Гармонические колебания
Линейная зависимость и линейная независимость системы функций
Линейная зависимость и линейная независимость системы функций
Исследование линейной независимости системы функций
Линейная независимость решений линейного дифференциального уравнения
Структура решения линейного ОДУ n-го порядка
Фундаментальная система решений однородного линейного дифференциального уравнения
Структура общего решения линейного однородного уравнения
Структура общего решения линейного неоднородного уравнения
Метод вариации произвольных постоянных отыскания частного решения
Линейные ОДУ с постоянными коэффициентами
Решение однородного уравнения с постоянными коэффициентами
Метод подбора построения частного решания неоднородного уравнения
Системы дифференциальных уравнений
Системы обыкновенных дифференциальных уравнений. Основные понятия
Фазовое пространство Фазовые траектории
Существование и единственность решения задачи Коши
Интегрирование систем дифференциальных уравнений методом исключения
Линейные системы OДУ. Структура решения
Линейные системы ОДУ. Основные понятия
Фундаментальная матрица решений однородной линейной системы дифференциальных уравнений
Структура общего решения однородной линейной системы дифференциальных уравнений
Структура общего решения неоднородной линейной системы дифференциальных уравнений
Системы ОДУ. Поведение решений
Устойчивость решений систем дифференциальных уравнений
Устойчивость и асимптотическая устойчивость по Ляпунову
Устойчивость положения равновесия линейных систем ОДУ
Устойчивость точек покоя нелинейных систем по линейному приближению
Неустойчивость по линейному приближению точек покоя нелинейных систем
Автономные системы дифференциальных уравнений
Автономные системы. Основные понятия
Фазовая плоскость, фазовые кривые, фазовый портрет автономной системы 2-го порядка
Векторное поле автономной системы 2-го порядка
Точки покоя линейной автономной системы 2-го порядка с постоянными коэффициентами
Рассмотрим обыкновенное дифференциальное уравнение 1–го порядка
Пусть y = y(x) решение уравнения.
Интегральная кривая y = y(x) имеет касательную с угловым коэффициентом k = f(x, y(x)). Это означает, что через каждую точку (x, y) области определения функции f(x, y) можно провести небольшой отрезок с угловым коэффициентом k = f(x, y(x)).
Выполнив такое построение для всех узлов некоторой прямоугольной сетки в области определения правой части уравнения , получим изображение поля направлений.Когда узлы сетки расположены "достаточно часто" поле направлений дает полную картину поведения интегральных кривых.
Метод изоклин — приближенный графический метод решения обыкновенных дифференциальных уравнений 1–го порядка.
Метод позволяет "вручную" (без использования компьютера) построить изображение поля направлений и по этому изображению построить интегральную кривую, проходящую через заданную точку.Рассмотрим линии, в каждой точке которых угловой коэффициент интегральных кривых имеет одно и то же постоянное значение: f(x, y) = k, k = const.
Такие кривые называются изоклинами дифференциального уравнения y' = f(x, y). Равенство f(x, y) = k — уравнение изоклины.В каждой точке (x, y) изоклины f(x, y) =k интегральные кривые уравнения имеют один и тот же угол наклона αrctg(α) = k.
Метод изоклин состоит в следующем.Строим достаточно густую сетку изоклин для различнх значений k и на каждой изоклине изображаем небольшие отрезки с наклоном k.
Затем, начиная из точки (x0, y0), поводим линию, которая, будет пересекать каждую изоклину под углом, заданным полем направлений. Полученная таким образом кривая и будет приближенным изображением (эскизом) интегральной кривой уравнения, проходящей через точку (x0, y0).
На рисунке изображены изоклины для k = 1,2, … ,15,16 и интегральная кривая, проходящая через точку (0,0) .
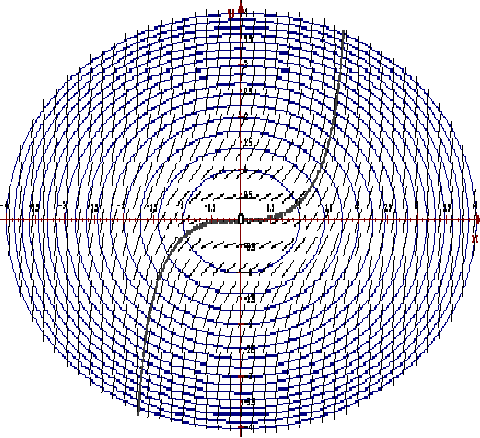
Метод изоклин как метод приближенного решения задачи Коши устарел. В его в основе лежит алгоритм изображения фрагмента поля направления, а современные компьютеры могут мгновенно и как угодно подробно нарисовать поле направлений, и достаточно точно изобразить интегральную кривую.
Однако, метод изоклин эффективно работает как инструмент исследования поведения решений. Он позволяет изобразить области характерного поведения интегральных кривых.
Например, изоклина f(x, y) = 0 — геометрическое место стационарных точек решения дифференциального уравнения, изоклины f(x, y) = k с большими значениями k показывают области быстрого роста решений и т.п.
На рисунке показано, как помогают изоклины "увидеть" точки экстремума интегральной кривой и судить о поведении решений дифференциального уравнения.
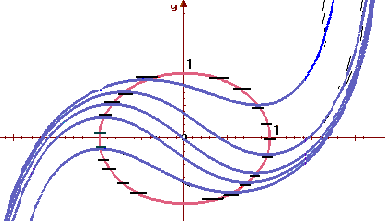
| Примеры |