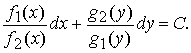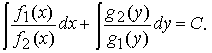| ОГЛАВЛЕНИЕ | ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ | ПОЛЕЗНЫЕ ССЫЛКИ |
Высшая математика
Обыкновенные дифференциальные уравнения и системы
Обыкновенные дифференциальные уравнения. Основные понятия
Связь ОДУ высших порядков и систем ОДУ
ОДУ 1-го порядка. Методы решения
Дифференциальные уравнения 1-го порядка. Основные понятия
Уравнения с разделяющимися переменными
Однородные уравнения 1-го порядка
Уравнения, приводящиеся к однородным
Уравнением с разделенными переменными называется дифференциальное уравнение вида
f(x)dx + g(y)dy = 0
с непрерывными функциями f(х) и g(y).
Равенство
где C — произвольная постоянная, определяет общий интеграл уравнения с разделёнными переменными.
Начальное условие для уравнения f(x)dx + g(y)dy = 0 можно задавать в виде y(x0) = y0 или в виде x(y0) = x0 .
Уравнением с разделяющимися переменными называется дифференциальное уравнение вида
Функции f1(x), g1(y), f2(x), g2(y) непрерывны в cвоих областях определения и g1(y)f2(x) ≠ 0 .
Разделив обе части уравнения на отличное от нуля произведение g1(y)f2(x), получим уравнение с разделенными переменными
Общий интеграл этого уравнения имеет вид
Решение уравнения в области, где g1(y)f2(x) = 0 требует специального обсуждения.
| Примеры | Решить свою задачу |