| ОГЛАВЛЕНИЕ | ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ | ПОЛЕЗНЫЕ ССЫЛКИ |
Высшая математика
Обыкновенные дифференциальные уравнения и системы
Обыкновенные дифференциальные уравнения. Основные понятия
Связь ОДУ высших порядков и систем ОДУ
Системы дифференциальных уравнений
Системы обыкновенных дифференциальных уравнений. Основные понятия
Фазовое пространство Фазовые траектории
Существование и единственность решения задачи Коши
Интегрирование систем дифференциальных уравнений методом исключения
Линейные системы OДУ. Структура решения
Системы ОДУ. Поведение решений
Автономные системы дифференциальных уравнений
Автономные системы. Основные понятия
Фазовая плоскость, фазовые кривые, фазовый портрет автономной системы 2-го порядка
Векторное поле автономной системы 2-го порядка
Точки покоя линейной автономной системы 2-го порядка с постоянными коэффициентами
Рассмотрим линейную автономную систему 2-го порядка с постоянными коэффициентами x' = A·x :
Такая система имеет единственную точку покоя x ≡ 0, x=0, y=0, (0, 0).
Характер точки покоя (её устойчивость, асимптотическую устойчивость, неустойчивость) можно установить по собственным значениям λ1, λ2 матрицы системы A.
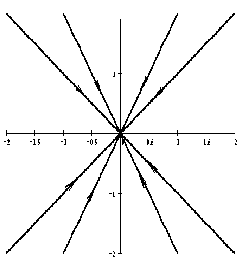
Если λ1, λ2 — разные действительные отрицательные числа, то точка покоя асимптотически устойчива, такая точка покоя называется устойчивый узел.
На рисунке приведен фрагмент фазового портрета в окрестности устойчивого узла.
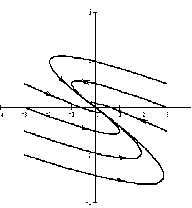
Если λ1, λ2 — разные действительные положительные числа, то точка покоя неустойчива, такая точка покоя называется неустойчивый узел.
На рисунке приведен фрагмент фазового портрета в окрестности неустойчивого узла.
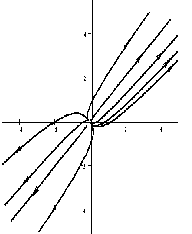
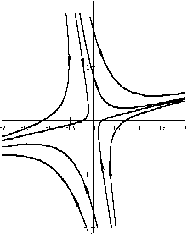
Если λ1, λ2 — действительные числа разных знаков, то точка покоя неустойчива, такая точка покоя называется седло.
На рисунке приведен фрагмент фазового портрета в окрестности седла.
Если λ1, λ2 — комплексные числа, λ1,2= Reλ ± iImλ, и Reλ ≤ 0, то точка покоя устойчива.
Если λ1, λ2 — комплексные числа, λ1,2= Reλ ± iImλ, и Reλ = 0, то точка покоя устойчива, но не асимптотически устойчива, такая точка покоя называется центром.
На рисунке приведен фрагмент фазового портрета в окрестности центра.
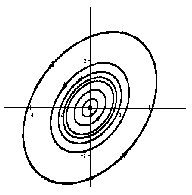
Если λ1, λ2 — комплексные числа, λ1,2= Reλ ± iImλ, и Reλ < 0, то точка покоя асимптотически устойчива, такая точка покоя называется устойчивым фокусом.
На рисунке приведен фрагмент фазового портрета в окрестности устойчивого фокуса.
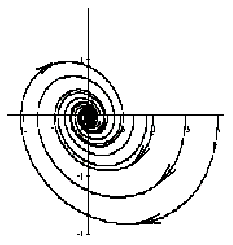
Если λ1, λ2 — комплексные числа, λ1,2= Reλ ± iImλ, и Reλ > 0, то точка покоя неустойчива, такая точка покоя называется неустойчивым фокусом.
На рисунке приведен фрагмент фазового портрета в окрестности неустойчивого фокуса.
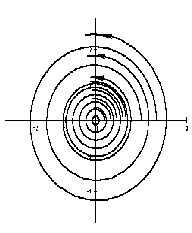
Если λ1= λ2 ≠ 0 — действительные положительные числа, то точка — узел специального вида — диакритический узел;
при λ1= λ2 < 0 — устойчивый диакритический узел;
при λ1= λ2 > 0 — неустойчивый диакритический узел.
На рисунке приведен фрагмент фазового портрета в окрестности устойчивого диакритического узла.
Если λ1= 0, λ2 ≠ 0, то существует прямая, проходящая через начало координат, все точки которой являются точками покоя.
Если λ1= λ2 = 0, то все точки плоскости являются точками покоя системы.
| Примеры |