ЛИНЕЙНЫЕ УРАВНЕНИЯ 2-ГО ПОРЯДКА. ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ

 
ОГЛАВЛЕНИЕ ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ ПОЛЕЗНЫЕ ССЫЛКИ

Высшая математика

Обыкновенные дифференциальные уравнения и системы

Обыкновенные дифференциальные уравнения. Основные понятия

Системы ОДУ. Основные понятия

Связь ОДУ высших порядков и систем ОДУ

ОДУ 1-го порядка

ОДУ 1-го порядка. Методы решения

Дифференциальные уравнения 1-го порядка. Основные понятия

Уравнения с разделяющимися переменными

Однородные уравнения 1-го порядка

Уравнения, приводящиеся к однородным

Линейные уравнения 1-го порядка

Уравнения Бернулли

Уравнения в полных дифференциалах

ОДУ 1-го порядка. Поведение решений

Теорема существования и единственности решения задачи Коши

Уравнения 1-го порядка. Поле направлений

Автономные уравнения 1-го порядка

Устойчивость решений ОДУ 1-го порядка

Асимптотическая устойчивость решений ОДУ 1-го порядка

Приближённые методы решения

Метод изоклин

Метод Эйлера

ОДУ высших порядков

ОДУ высших порядков. Понижение порядка

Понижение порядка ОДУ. Введение

Уравнения, не содержащие независимой переменной

Уравнения, не содержащие искомой функции

Уравнения с однородной правой частью

Линейные ОДУ n-го порядка

Линейные ОДУ n-го порядка. Введение

Свойства решений линейного уравнения. Принцип суперпозиции

Существование и единственность решения задачи Коши

Линейные уравнения второго порядка. Гармонические колебания

Линейные уравнения 2-го порядка. Ангармонические колебания

Линейные уравнения 2-го порядка. Уравнение Ньютона

Линейная зависимость и линейная независимость системы функций

Линейная зависимость и линейная независимость системы функций

Определитель Вронского

Исследование линейной независимости системы функций

Линейная независимость решений линейного дифференциального уравнения

Структура решения линейного ОДУ n-го порядка

Фундаментальная система решений однородного линейного дифференциального уравнения

Структура общего решения линейного однородного уравнения

Структура общего решения линейного неоднородного уравнения

Метод вариации произвольных постоянных отыскания частного решения

Линейные ОДУ с постоянными коэффициентами

Решение однородного уравнения с постоянными коэффициентами

Метод подбора построения частного решания неоднородного уравнения

Уравнение Эйлера

Системы дифференциальных уравнений

Системы обыкновенных дифференциальных уравнений. Основные понятия

Фазовое пространство Фазовые траектории

Существование и единственность решения задачи Коши

Интегрирование систем дифференциальных уравнений методом исключения

Линейные системы OДУ. Структура решения

Линейные системы ОДУ. Основные понятия

Фундаментальная матрица решений однородной линейной системы дифференциальных уравнений

Структура общего решения однородной линейной системы дифференциальных уравнений

Структура общего решения неоднородной линейной системы дифференциальных уравнений

Построение фундаментальной матрицы решений однородной линейной системы дифференциальных уравнений с постоянными коэффициентами методом Эйлера

Системы ОДУ. Поведение решений

Устойчивость решений систем дифференциальных уравнений

Устойчивость и асимптотическая устойчивость по Ляпунову

Устойчивость положения равновесия линейных систем ОДУ

Устойчивость точек покоя нелинейных систем по линейному приближению

Неустойчивость по линейному приближению точек покоя нелинейных систем

Автономные системы дифференциальных уравнений

Автономные системы. Основные понятия

Свойства фазовых траекторий

Фазовая плоскость, фазовые кривые, фазовый портрет автономной системы 2-го порядка

Векторное поле автономной системы 2-го порядка

Точки покоя линейной автономной системы 2-го порядка с постоянными коэффициентами

Численные методы решения ОДУ

Метод Эйлера

Методы Рунге-Кутты

Многошаговые методы

Жёсткие системы. Методы численного решения

Рассмотрим линейное однородное дифференциальное уравнение 2–го порядка (ω>0 — постоянная величина)

y '' + ω2 y = 0 .

Легко видеть, что общее решение этого уравнения имеет вид

y(t) = C1cos(ωt) + C2sin(ωt) .

Его можно записать в виде

y(t) = Acos(ωt − φ) ,

Для произвольной точки (t0, y0, y1) решение задачи Коши   y(t0) = y0, y'(t0) = y1 существует и единственно на всей числовой оси .

Пусть t0 = 0. Решение задачи Коши    y(0) = y0,  y'(0) = y1  имеет вид

y(x) = Acos(ωt − φ) ,

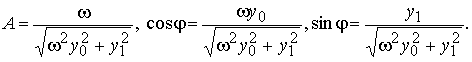
Будем считать, что y(t) — координата частицы в момент времени t . Частица движется по оси y из начальной точки y0 с положительной скоростью y1 > 0 .

Поскольку |y(x)| = |Acos(ωt − φ)| ≤ A , то частица будет двигаться по оси внутри отрезка [− A,A] .

Сначала частица движется вправо до точки y = A . В точку y = A она придет в момент времени  t = (π + φ)/ω, (когда y(t) = Acos(ωt − φ) = A).

Затем частица движется влево до точки y = − A . В точку y = − A частица придет в момент времени   t = (2π + φ)/ω, (когда y(t) = Acos(ωt − φ) = − A).

Понятно, что частица совершает периодические колебания на отрезке [− A, A] с периодом T = 2π/ω .

Число A называется амплитудой колебаний. Число ω называется частотой колебаний. Период колебаний T = 2π/ω не зависит от амплитуды.

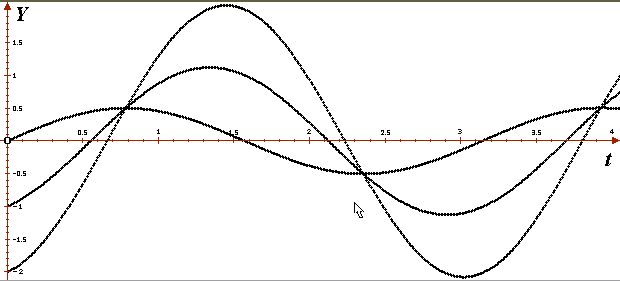
На рисунке изображены пути трех частиц, движение которых описывается уравнением y '' + 4y = 0 .

Частицы движутся со скоростью y1 = 1 из начальных точек y0 = − 2, − 1, 0:  

 

Физическая система, которая описывается уравнением y '' + ω2 y = 0 , называется гармоническим осциллятором.

Это малые колебания маятника, малые колебания под действием силы тяжести груза, подвешенного на упругой пружине, электрические колебания в контуре, состоящем из емкости и индуктивности и т.п.

  Примеры Решить свою задачу

© МЭИ (ТУ) 2007