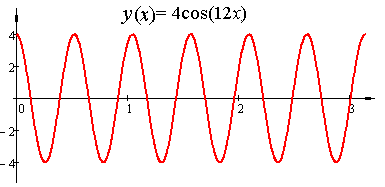| ОГЛАВЛЕНИЕ | ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ | ПОЛЕЗНЫЕ ССЫЛКИ |
Высшая математика
Обыкновенные дифференциальные уравнения и системы
Обыкновенные дифференциальные уравнения. Основные понятия
Связь ОДУ высших порядков и систем ОДУ
ОДУ высших порядков. Понижение порядка
Линейные ОДУ n-го порядка. Введение
Свойства решений линейного уравнения. Принцип суперпозиции
Существование и единственность решения задачи Коши
Линейные уравнения второго порядка. Гармонические колебания
Линейная зависимость и линейная независимость системы функций
Запишем дифференциальное уравнение малых колебаний маятника c периодом колебаний T = π/6 и амплитудой 4.
Поскольку дифференциальное уравнение, описывающее малые колебания маятника с периодом T = 2π/ω имеет вид y '' + ω2 y = 0, то колебания маятника с периодом T = π / 6 описываются уравнением с параметром ω = 2π/T = 12:y '' + 144 y = 0.
Амплитуду колебаний определим из начальных условий y(0) = 4 , y'(0) = 0 .
Действительно, поскольку, y(t) = C1cos(ωt) + C2sin(ωt), то y(0) = C1cos(0) + C2sin(0) = С1 = 4, y '(0) = − ωC1sin(0) + ωC2cos(0) = ωC2 = 0, С1 = 4, С2 = 0, y(t) = 4cos(12t) ,
т.е. амплитуда колебаний равна 4 .
Итак, малые колебания маятника c периодом колебаний T = π/6 и амплитудой 4 описываются решением y(t) = 4cos(12t) задачи Коши
y '' + 144 y = 0, y(0) = 4 , y '(0) = 0.
| Решить свою задачу |