УРАВНЕНИЯ С РАЗДЕЛЯЮЩИМИСЯ ПЕРЕМЕННЫМИ. Примеры

 
ОГЛАВЛЕНИЕ ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ ПОЛЕЗНЫЕ ССЫЛКИ

Высшая математика

Обыкновенные дифференциальные уравнения и системы

Обыкновенные дифференциальные уравнения. Основные понятия

Системы ОДУ. Основные понятия

Связь ОДУ высших порядков и систем ОДУ

ОДУ 1-го порядка

ОДУ 1-го порядка. Методы решения

Дифференциальные уравнения 1-го порядка. Основные понятия

Уравнения с разделяющимися переменными

Однородные уравнения 1-го порядка

Уравнения, приводящиеся к однородным

Линейные уравнения 1-го порядка

Уравнения Бернулли

Уравнения в полных дифференциалах

ОДУ 1-го порядка. Поведение решений

Приближённые методы решения

ОДУ высших порядков

Системы дифференциальных уравнений

Численные методы решения ОДУ
Равенство 2x2 − 6x + 3y2 = 8 определяет частный интеграл задачи Коши для уравнения с разделёнными переменными (2x − 3)dx +3ydy = 0, y(1) = 2.

Действительно. Поскольку

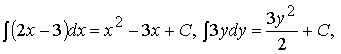
то выражение

2x2 − 6x + 3y2 = C,

где C — произвольная постоянная, определяет общий интеграл уравнения с разделёнными переменными.

Подставив x = 1, y = 2 имеем C = 8, то есть 2x2 − 6x + 3y2 = 8 — частный интеграл, задающий в неявной форме решение задачи Коши с начальным условием y(1) = 2.

Равенство 2x2 − 6x + 3y2 = 8 определяет соответствующую интегральную кривую — линию на плоскости, проходящую через точку M0(1, 2):

  Ещё Решить свою задачу

© МЭИ (ТУ) 2007