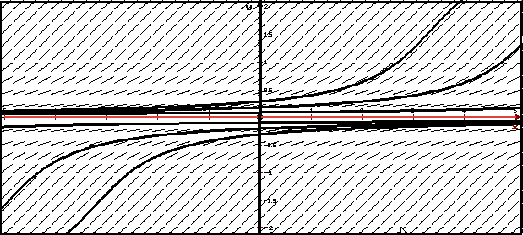
На рисунке красным изображено неустойчивое решение y = 0 задачи Коши y' = sin² y, y(0) = 0.

Легко видеть, что функция y = 0 — решение задачи Коши y' = sin² y  , y(0) = 0, что при   x ≥ 0 существует общее решение уравнения  y' = sin² y, которое  имеет вид  y = arcctg(x +C),

и что решением задачи Коши y' = sin² y , y(0) =y₀   является функция  y( x) = arcctg(x + ctg y₀).

Положим ε = π/2. При x → ∞ справедливо

|y(x) − φ(x) | = |arcctg(x + ctg y₀)− 0 | = |arcctg(x + ctg y₀) | → π.

Но тогда, как бы ни было мало δ > 0 такое, что

|y(x₀) − φ(x₀) | = |y(0) − φ(0) | = |y₀− 0 | = | y₀ | < δ ,

найдётся такое x₁ > 0, что при всех   x >x₁

|y(x) − φ(x) | > π/2 = ε .

Таким образом мы показали аналитически, что решение y = 0 — неустойчивое решение уравнения.