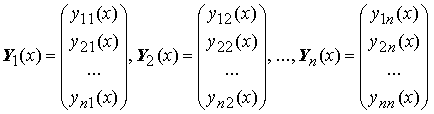| ОГЛАВЛЕНИЕ | ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ | ПОЛЕЗНЫЕ ССЫЛКИ |
Определитель Вронского линейно независимой системы функций может быть тождественно равен нулю.
Рассмотрим две функции:
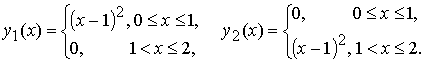
Эти функции линейно независимы на [0, 2]. Действительно:
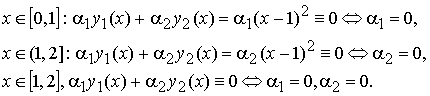
Вычислим определитель Вронского W(x; y1(x), y2(x)) на [0, 2]:
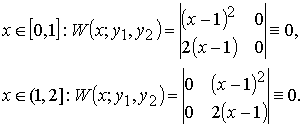
Итак, функции линейно независимы на [0, 2], а W(x; y1(x), y2(x)) ≡ 0 на [0, 2].
Этот пример означает, что тождественное равенство нулю определителя Вронского системы функций является необходимым условием линейной зависимости системы функций, но не является достаточным условием линейной зависимости системы функций.
С другой строны, отличие от тождественного нуля определителя Вронского системы функций является достаточным условием условием линейной независимости системы функций.
(Ведь если бы она была бы линейно зависима, то определитель Вронского был бы тождественным нулём).
называется определитель W[x; Y1, Y2, ..., Yn], заданный равенством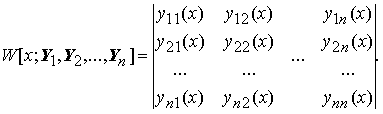


 Обыкновенные дифференциальные уравнения и системы
Обыкновенные дифференциальные уравнения и системы Обыкновенные дифференциальные уравнения. Основные понятия
Обыкновенные дифференциальные уравнения. Основные понятия