| ОГЛАВЛЕНИЕ | ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ | ПОЛЕЗНЫЕ ССЫЛКИ |
Высшая математика
Обыкновенные дифференциальные уравнения и системы
Обыкновенные дифференциальные уравнения. Основные понятия
Связь ОДУ высших порядков и систем ОДУ
ОДУ 1-го порядка. Методы решения
Дифференциальные уравнения 1-го порядка. Основные понятия
Уравнения с разделяющимися переменными
Однородные уравнения 1-го порядка
Уравнения, приводящиеся к однородным
ОДУ 1-го порядка. Поведение решений
Теорема существования и единственности решения задачи Коши
Уравнения 1-го порядка. Поле направлений
Автономные уравнения 1-го порядка
ОДУ высших порядков. Понижение порядка
Понижение порядка ОДУ. Введение
Уравнения, не содержащие независимой переменной
Линейные ОДУ n-го порядка. Введение
Свойства решений линейного уравнения. Принцип суперпозиции
Существование и единственность решения задачи Коши
Линейные уравнения второго порядка. Гармонические колебания
Линейная зависимость и линейная независимость системы функций
Линейная зависимость и линейная независимость системы функций
Исследование линейной независимости системы функций
Линейная независимость решений линейного дифференциального уравнения
Структура решения линейного ОДУ n-го порядка
Фундаментальная система решений однородного линейного дифференциального уравнения
Структура общего решения линейного однородного уравнения
Структура общего решения линейного неоднородного уравнения
Метод вариации произвольных постоянных отыскания частного решения
Линейные ОДУ с постоянными коэффициентами
Решение однородного уравнения с постоянными коэффициентами
Метод подбора построения частного решания неоднородного уравнения
Системы дифференциальных уравнений
Системы обыкновенных дифференциальных уравнений. Основные понятия
Фазовое пространство Фазовые траектории
Существование и единственность решения задачи Коши
Интегрирование систем дифференциальных уравнений методом исключения
Линейные системы OДУ. Структура решения
Линейные системы ОДУ. Основные понятия
Фундаментальная матрица решений однородной линейной системы дифференциальных уравнений
Структура общего решения однородной линейной системы дифференциальных уравнений
Структура общего решения неоднородной линейной системы дифференциальных уравнений
Системы ОДУ. Поведение решений
Устойчивость решений систем дифференциальных уравнений
Устойчивость и асимптотическая устойчивость по Ляпунову
Устойчивость положения равновесия линейных систем ОДУ
Устойчивость точек покоя нелинейных систем по линейному приближению
Неустойчивость по линейному приближению точек покоя нелинейных систем
Автономные системы дифференциальных уравнений
Автономные системы. Основные понятия
Фазовая плоскость, фазовые кривые, фазовый портрет автономной системы 2-го порядка
Векторное поле автономной системы 2-го порядка
Точки покоя линейной автономной системы 2-го порядка с постоянными коэффициентами
Посмотрим как можно найти методом Лагранжа частное решение для уравнения 2–го порядка y'' + a1(x)y' + a0(x)y = f(x) с нерерывными коэффициентами и непрерывной правой частью.
Предположим, что известна фундаментальная система y1(x), y2(x) решений соответствующего однородного уравнения y'' + a1(x)y' + a0(x)y = 0.
Будем искать частное решение неоднородного уравнения в виде
y*(x) = C1(x) y1(x) + C2(x) y2(x),
где C1(x), C2(x) — такие неизвестные, дважды дифференцируемые на [a; b] функции.
Для того чтобы подставить функцию y*(x) в исходное уравнение, найдём сначала первую производную y*(x):
(y*(x))' = C1'(x) y1(x) + C1(x) y1'(x) + C2'(x) y2(x) + C2(x) y2'(x).
Будем искать C1(x), C2(x) такими, чтобы C1'(x) y1(x) + C2'(x) y2(x) = 0 и, следовательно,
(y*(x))' = C1(x) y1'(x) + C2(x) y2'(x).
Тогда
(y*(x))'' = C1'(x) y1'(x) + C1(x) y1''(x) + C2'(x) y2'(x) + C2(x) y2''(x).
Подставим выражения для производных в уравнение:
y'' + a1(x)y' + a0(x)y ≡ C1'(x) y1'(x) + C1(x) y1''(x) + C2'(x) y2'(x) + C2(x) y2''(x) + a1(x)(C1(x) y1'(x) + C2(x) y2'(x)) + a0(x)(C1(x) y1(x) + C2(x) y2(x)) = f(x).
После простых преобразований имеем:
C1(x)(y1'' + a1(x)y1' + a0(x)y1) + C2(x)(y2'' + a1(x)y2' + a0(x)y2) + C1'(x) y1'(x) + C2'(x) y2'(x) = f(x).
Но поскольку y1(x), y2(x) — решения однородного уравнения y'' + a1(x)y' + a0(x)y = 0, то
C1'(x) y1'(x) + C2'(x) y2'(x) = f(x).
Для неизвестных функций C1(x), C2(x) получили систему линейных дифференциальных уравнений второго порядка:
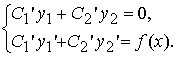
Определитель этой линейной относительно C1'(x), C2'(x) системы — это отличный от нуля на [a; b] вронскиан фундаментальной системы решений.
Следовательно, система имеет единственное решение, которое можно выписать в явном виде (имеем два дифференциальных уравнения первого порядка):
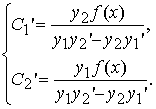
Эти дифференциальные уравнения первого порядка с разделяющимися переменными легко интегрируются:
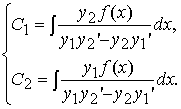
Неизвестные варьируемые постоянные найдены — найдено частное решение линейного неоднородного уравнения второго порядка.
| Пример |