| ОГЛАВЛЕНИЕ | ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ | ПОЛЕЗНЫЕ ССЫЛКИ |
Высшая математика
Обыкновенные дифференциальные уравнения и системы
Обыкновенные дифференциальные уравнения. Основные понятия
Связь ОДУ высших порядков и систем ОДУ
ОДУ 1-го порядка. Методы решения
Дифференциальные уравнения 1-го порядка. Основные понятия
Уравнения с разделяющимися переменными
Однородные уравнения 1-го порядка
Уравнения, приводящиеся к однородным
ОДУ 1-го порядка. Поведение решений
Теорема существования и единственности решения задачи Коши
Уравнения 1-го порядка. Поле направлений
Автономные уравнения 1-го порядка
ОДУ высших порядков. Понижение порядка
Понижение порядка ОДУ. Введение
Уравнения, не содержащие независимой переменной
Линейные ОДУ n-го порядка. Введение
Свойства решений линейного уравнения. Принцип суперпозиции
Существование и единственность решения задачи Коши
Линейные уравнения второго порядка. Гармонические колебания
Линейная зависимость и линейная независимость системы функций
Линейная зависимость и линейная независимость системы функций
Исследование линейной независимости системы функций
Линейная независимость решений линейного дифференциального уравнения
Структура решения линейного ОДУ n-го порядка
Фундаментальная система решений однородного линейного дифференциального уравнения
Структура общего решения линейного однородного уравнения
Структура общего решения линейного неоднородного уравнения
Метод вариации произвольных постоянных отыскания частного решения
Линейные ОДУ с постоянными коэффициентами
Решение однородного уравнения с постоянными коэффициентами
Метод подбора построения частного решания неоднородного уравнения
Системы дифференциальных уравнений
Системы обыкновенных дифференциальных уравнений. Основные понятия
Фазовое пространство Фазовые траектории
Существование и единственность решения задачи Коши
Интегрирование систем дифференциальных уравнений методом исключения
Линейные системы OДУ. Структура решения
Линейные системы ОДУ. Основные понятия
Фундаментальная матрица решений однородной линейной системы дифференциальных уравнений
Структура общего решения однородной линейной системы дифференциальных уравнений
Структура общего решения неоднородной линейной системы дифференциальных уравнений
Системы ОДУ. Поведение решений
Устойчивость решений систем дифференциальных уравнений
Устойчивость и асимптотическая устойчивость по Ляпунову
Устойчивость положения равновесия линейных систем ОДУ
Устойчивость точек покоя нелинейных систем по линейному приближению
Неустойчивость по линейному приближению точек покоя нелинейных систем
Автономные системы дифференциальных уравнений
Автономные системы. Основные понятия
Фазовая плоскость, фазовые кривые, фазовый портрет автономной системы 2-го порядка
Векторное поле автономной системы 2-го порядка
Точки покоя линейной автономной системы 2-го порядка с постоянными коэффициентами
Уравнением колебаний называют линейное неоднородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами
Однородное уравнение y'' + ω02y = 0 описывает свободные колебания материальной точки с частотой ω02.
Неоднородное уравнение — колебания материальной точки под действием внешней периодической силы Fcosω0x, частота которой ω0 совпадает с частотой свободных колебаний частицы (резонанс).
Найдём общее решение уравнения колебаний в случае, когда частота свободных колебаний совпадает с частотой внешней вынуждающей силы.
Характеристическое уравнение однородного уравнения λ2 + ω02 = 0 имеет пару комплексно сопряжённых корней λ1,2 = ± i ω0.
Фундаментальную систему решений однородного уравнения образуют функции cosω0x, sinω0x. Общее решение однородного уравнения имеет вид
y(x, C1, C2) = C1cosω0x + C2sinω0x.
Правая часть уравнения — квазимногочлен exp(αx)(Mm(x)cos(βx) + Nn(x)sin(βx))≡Fcosω0x , у которого α = 0, β = ω, Mm(x)= M0 = F, Nn(x)= 0, α ± iβ = iω0.
Среди коренй характеристического уравнения есть одна пара комплексно сопряжённых корней, равная α ± iβ = iω0: λ1,2 = ± i ω0.
Поэтому будем искать частное решение неоднородного уравнения y*(x) в виде y*(x) =( A cosω x + B sin ω x)x.
Подставим в уранение:
y = (A cosω x + B sin ω x)x,
y' = (−Aω sinω x + B ωcos ω x)x + (A cosω x + B sin ω x),
y'' = (−Aω2 cosω x − Bω2 sin ω x)x + 2(−Aω sinω x + B ωcos ω x)x ,
y'' + ω02y = (−Aω2 cosω x − Bω2 sin ω x)x + 2(−Aω sinω x + B ωcos ω x)x + ω02(A cosω x + B sin ω x)x = 2Bω0cosω0 x − 2 A sin ω0 x = Fcos ω0x.
Приравняв коэффициенты в левой и правой части уравнения 2Bω0cosω0 x − 2 A sin ω0 x = Fcos ω0x, получим A = 0, B = F/2ω0 и тогда частное решение неоднородного уравнения
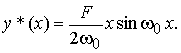
Теперь можно записать общее решение неоднородного уравнения
