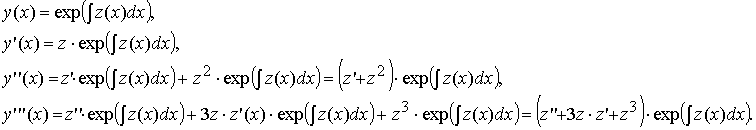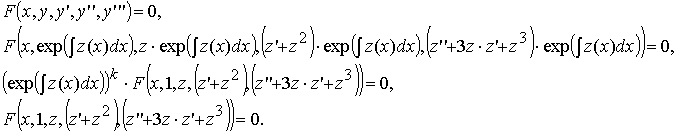| ОГЛАВЛЕНИЕ | ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ | ПОЛЕЗНЫЕ ССЫЛКИ |
Высшая математика
Обыкновенные дифференциальные уравнения и системы
Обыкновенные дифференциальные уравнения. Основные понятия
Связь ОДУ высших порядков и систем ОДУ
ОДУ высших порядков. Понижение порядка
Понижение порядка ОДУ. Введение
Уравнения, не содержащие независимой переменной
Линейная зависимость и линейная независимость системы функций
Рассмотрим, например, уравнение третьего порядка, однородное относительно неизвестной функции и всех ее производных:
F(x, y, y', y'', y''') = 0,
F(x, y, y', y'', y''') = tk F(x, y, y', y'', y''').
Посмотрмм, как прядок такого уравнения можно понизить до второго, используя замену
Выразим y', y'', y''' через z(x):
Произведя замену, получим дифференциальное уравнение второго порядка:
В итоге получено дифференциальное уравнение второго порядка относительно z(x):
Φ(x, z, z', z'') = 0.