| ОГЛАВЛЕНИЕ | ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ | ПОЛЕЗНЫЕ ССЫЛКИ |
Высшая математика
Обыкновенные дифференциальные уравнения и системы
Обыкновенные дифференциальные уравнения. Основные понятия
Связь ОДУ высших порядков и систем ОДУ
ОДУ 1-го порядка. Методы решения
Дифференциальные уравнения 1-го порядка. Основные понятия
Уравнения с разделяющимися переменными
Однородные уравнения 1-го порядка
Уравнения, приводящиеся к однородным
ОДУ 1-го порядка. Поведение решений
Теорема существования и единственности решения задачи Коши
Уравнения 1-го порядка. Поле направлений
Автономные уравнения 1-го порядка
ОДУ высших порядков. Понижение порядка
Понижение порядка ОДУ. Введение
Уравнения, не содержащие независимой переменной
Линейные ОДУ n-го порядка. Введение
Свойства решений линейного уравнения. Принцип суперпозиции
Существование и единственность решения задачи Коши
Линейные уравнения второго порядка. Гармонические колебания
Линейная зависимость и линейная независимость системы функций
Линейная зависимость и линейная независимость системы функций
Исследование линейной независимости системы функций
Линейная независимость решений линейного дифференциального уравнения
Структура решения линейного ОДУ n-го порядка
Фундаментальная система решений однородного линейного дифференциального уравнения
Структура общего решения линейного однородного уравнения
Структура общего решения линейного неоднородного уравнения
Метод вариации произвольных постоянных отыскания частного решения
Линейные ОДУ с постоянными коэффициентами
Решение однородного уравнения с постоянными коэффициентами
Метод подбора построения частного решания неоднородного уравнения
Системы дифференциальных уравнений
Системы обыкновенных дифференциальных уравнений. Основные понятия
Фазовое пространство Фазовые траектории
Существование и единственность решения задачи Коши
Интегрирование систем дифференциальных уравнений методом исключения
Линейные системы OДУ. Структура решения
Линейные системы ОДУ. Основные понятия
Фундаментальная матрица решений однородной линейной системы дифференциальных уравнений
Структура общего решения однородной линейной системы дифференциальных уравнений
Структура общего решения неоднородной линейной системы дифференциальных уравнений
Системы ОДУ. Поведение решений
Устойчивость решений систем дифференциальных уравнений
Устойчивость и асимптотическая устойчивость по Ляпунову
Устойчивость положения равновесия линейных систем ОДУ
Устойчивость точек покоя нелинейных систем по линейному приближению
Неустойчивость по линейному приближению точек покоя нелинейных систем
Автономные системы дифференциальных уравнений
Автономные системы. Основные понятия
Фазовая плоскость, фазовые кривые, фазовый портрет автономной системы 2-го порядка
Векторное поле автономной системы 2-го порядка
Точки покоя линейной автономной системы 2-го порядка с постоянными коэффициентами
Геометрически устойчивость решения дифференциального уравнения, удовлетворяющего условию y( x0 ) = y0 , y = φ(x), φ(x0)= y0 , означает, что интегральные кривые y = y(x), близкие к интегральной кривой y = φ(x) в момент x = x0 , остаются близкими к ней и на всем промежутке [x0, ∞) .
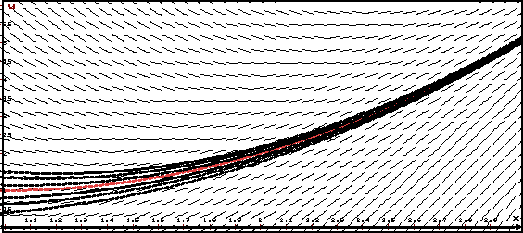
На рисунке красным изображено устойчивое решение задачи Коши y' = − y, y(1) = 1. Видно, что все интегральные кривые, близкие к этому решениюв начальный момент x = 1, остаются вблизи него и при x > 1 .
Устойчивость решения можно доказать аналитически.
Легко видеть, что общее решение уравнения y' = − y , имеет вид y = Cexp( − x). Решением задачи Коши y' = − y, y(1) = 1 является функция φ(x) = exp(1 − x),
а решение задачи Коши y' = − y, y(1) = y0 — функция y( x) = y0 exp(1 − x). Все эти решения существуют при x ≥ 1.
Возьмём произвольное ε > 0 и положим δ = ε.
Тогда, если |y(x0) − φ(x0) | = | y0 − 1 | < δ , то при всех x >1
|y(x) − φ(x) | = | y0 exp(1 − x) − exp(1 − x) | = | y0− 1 |· exp(1 − x) < | y0− 1 | < δ = ε ,
т.е. действительно, как показано на рисунке, решение φ(x) = exp(1 − x) устойчиво по Ляпунову.
| Ещё | Решить свою задачу |